-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2017; 6(2): 38-42
doi:10.5923/j.jgt.20170602.02

Worst Welfare under Supply Function Competition with Sequential Contracting in a Vertical Relationship
Aika Monden
Graduate School of Business Administration, Kobe University, Kobe, Japan
Correspondence to: Aika Monden, Graduate School of Business Administration, Kobe University, Kobe, Japan.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We compare equilibrium welfares under Cournot, Bertrand, and supply function competitions. Although it is a natural result that equilibrium outcomes under the supply function competition are intermediate between those under Cournot and Bertrand competitions, we show that the supply function competition may yield the smallest social welfare. To obtain this result, we consider a vertical market where an upstream firm sequentially contracts with two downstream firms.
Keywords: Supply function competition, Price discrimination, Sequential contracting
Cite this paper: Aika Monden, Worst Welfare under Supply Function Competition with Sequential Contracting in a Vertical Relationship, Journal of Game Theory, Vol. 6 No. 2, 2017, pp. 38-42. doi: 10.5923/j.jgt.20170602.02.
Article Outline
1. Introduction
- Fierce competition generally brings down price and raises social welfare. Recognizing this, antitrust authorities implement competition policies to intensify market competition. An index that can measure the competition intensity is the type of competition, that is, whether Cournot or Bertrand competition prevails. Previous studies focus on other indicators such as the number of firms and the degree of product differentiation, but regardless of the indicator is employed, tougher competition is desirable for society. Thus, several papers focus on a situation where equilibrium social welfare decreases with the competition intensity (Lahiri and Ono, 1988; Mukherjee and Zhao, 2009; Fanti, 2013). Thus, the literature on industrial organization compares outcomes under Cournot competition with those under Bertrand competition and finds that in many cases, Bertrand competition yields outcomes that are more desirable for society.For example, a classic study that compares Cournot competition with Bertrand competition is by Singh and Vives (1984). They show that the equilibrium price in Bertrand competition is lower than that in Cournot competition. Studies that followed indicate that this relationship is reversed (e.g., Delbono and Lambertin, 2016a; Häckner, 2000; Zanchettin, 2006).Some recent studies consider an intermediate competition type between Cournot and Bertrand competitions. One of them is supply function competition (Grossman, 1981; Klemperer and Meyer, 1989). Some recent studies analyze properties of supply function competitions (e.g., Delgado and Moreno, 2004; Ciarreta and Gutierrez-Hita, 2006; Menezes and Quiggin, 2012; Delbono and Lambertini, 2015, 2016b). Under the supply function competition, it is common wisdom that the supply function equilibrium is intermediate between that under Cournot and Bertrand (Delbono and Lambertini, 2015). However, Delbono and Lambertini (2016b) challenge this well-known result. They consider a market with quadratic cost and show that the supply function competition creates the largest social welfare among the competitions.Following Delbono and Lambertini (2016b), we reconsider a welfare ranking between Cournot, Bertrand, and the supply function competitions. There are some differences between our model and theirs. In particular, we consider a vertically related market where an upstream firm sequentially contracts with two downstream firms. Our formulation of a sequential contract is the same as that of Kim and Sim (2015). In other words, we introduce the supply function competition into the model with the sequential contract presented by Kim and Sim (2015).Because the supply function competition leads to Cournot and Bertrand equilibria as special cases, considering a supply function competition model suffices to examine whether Bertrand is the best outcome and Cournot, the worst. When comparing the two competition structures with other cases in the supply function competition, we show that Cournot and Bertrand competitions do not lead to the worst outcomes. That is, at parameter values where equilibrium outcomes are not the same as those under Cournot and Bertrand competitions, we obtain the minimum social welfare. This result is quite different from that in Delbono and Lambertini (2016b).The paper proceeds as follows. The next section presents the model. Section 3 calculates the equilibrium and provides the main results. Section 4 concludes the paper.
2. The Model
- We consider a market with upstream firm
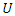 and two asymmetric downstream firms
and two asymmetric downstream firms 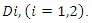 To produce one unit of product, each downstream firm must purchase one unit of input from the upstream firm. We assume that the upstream firm can choose different prices for the downstream firms. We denote the wholesale price for downstream firm
To produce one unit of product, each downstream firm must purchase one unit of input from the upstream firm. We assume that the upstream firm can choose different prices for the downstream firms. We denote the wholesale price for downstream firm 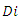 by
by 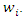 Let
Let 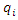 denote the output of downstream firm
denote the output of downstream firm 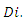 We assume that the marginal cost of upstream firm
We assume that the marginal cost of upstream firm 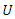 is zero, that of downstream firm
is zero, that of downstream firm 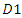 is also zero, and that of downstream firm
is also zero, and that of downstream firm 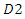 is
is 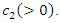 Following the literature on supply function competition, we assume that downstream firm
Following the literature on supply function competition, we assume that downstream firm 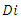 uses a linear supply function
uses a linear supply function 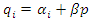 , where
, where 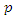 is the price, intercept
is the price, intercept 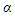 is an endogenous variable chosen by each firm, and
is an endogenous variable chosen by each firm, and 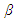 is an exogenous parameter.Menezes and Quiggin (2012) and Delbono and Lambertini (2015) show that as
is an exogenous parameter.Menezes and Quiggin (2012) and Delbono and Lambertini (2015) show that as 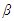 converges to zero, equilibrium outcomes under the supply function competition converge to those under Cournot competition; however, as
converges to zero, equilibrium outcomes under the supply function competition converge to those under Cournot competition; however, as 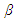 diverges to infinity, equilibrium outcomes converge to those under Bertrand competition. Therefore, to compare equilibria under Cournot, Bertrand, and the supply function competitions, it suffices to consider the supply function competition with
diverges to infinity, equilibrium outcomes converge to those under Bertrand competition. Therefore, to compare equilibria under Cournot, Bertrand, and the supply function competitions, it suffices to consider the supply function competition with 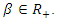 Moreover, as an increase in
Moreover, as an increase in 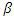 moves equilibrium outcomes closer to those in Bertrand competition, we can interpret
moves equilibrium outcomes closer to those in Bertrand competition, we can interpret 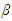 as the index of competition intensity. As downstream firm
as the index of competition intensity. As downstream firm 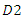 is relatively inefficient, for large
is relatively inefficient, for large 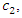 the equilibrium output of
the equilibrium output of 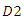 would take a value of zero. To guarantee a positive outcome, we assume
would take a value of zero. To guarantee a positive outcome, we assume 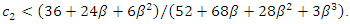 We assume that the inverse demand function is
We assume that the inverse demand function is 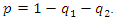 As we assume a linear supply function, substituting
As we assume a linear supply function, substituting 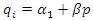 into the inverse demand function and solving it for
into the inverse demand function and solving it for 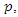 we have
we have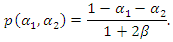 Substituting this equation into
Substituting this equation into 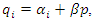 we have the following supply functions:
we have the following supply functions: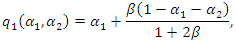
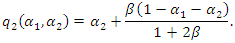 Using the above equations, we define the profits of downstream and upstream firms as follows:
Using the above equations, we define the profits of downstream and upstream firms as follows: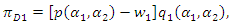
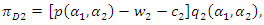
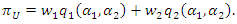 Consumer surplus
Consumer surplus 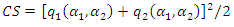 and social welfare
and social welfare 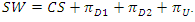 Following Kim and Sim (2015), we consider the sequential contracts between the upstream and downstream firms. In the first stage, the upstream firm decides wholesale price
Following Kim and Sim (2015), we consider the sequential contracts between the upstream and downstream firms. In the first stage, the upstream firm decides wholesale price 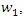 and in the second stage, downstream firm
and in the second stage, downstream firm 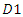 chooses
chooses 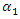 in its supply function. After these decisions, in the third stage, the upstream firm offers wholesale price
in its supply function. After these decisions, in the third stage, the upstream firm offers wholesale price 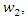 and in the fourth stage, downstream firm
and in the fourth stage, downstream firm 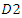 determines
determines 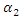 in its supply function. We could justify this timing of the game as follows. When the upstream firm already creates a long-term relationship with downstream firm
in its supply function. We could justify this timing of the game as follows. When the upstream firm already creates a long-term relationship with downstream firm 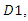 the contract may express a commitment effect. Then, given the contract with downstream firm
the contract may express a commitment effect. Then, given the contract with downstream firm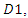 the upstream firm and downstream firm
the upstream firm and downstream firm 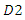 must negotiate their contract. Hence, a Stackelberg timing structure is a natural assumption here.We assume complete information. The model is solved by backward induction. Only pure strategies are considered throughout this paper.
must negotiate their contract. Hence, a Stackelberg timing structure is a natural assumption here.We assume complete information. The model is solved by backward induction. Only pure strategies are considered throughout this paper.3. Calculating Equilibrium and Condition Yielding Worst Welfare
- The profit maximization problem of downstream firm
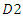 is
is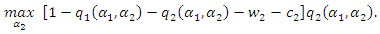 The first-order condition
The first-order condition 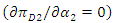 yields
yields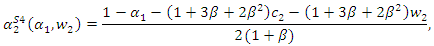 where superscript
where superscript  represents that the outcomes are in stage 4. Substituting this outcome into
represents that the outcomes are in stage 4. Substituting this outcome into 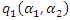 and
and 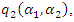 we have
we have 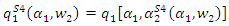 and
and 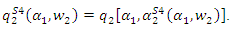 Substituting the above results into the profit of the upstream firm, the maximization problem is
Substituting the above results into the profit of the upstream firm, the maximization problem is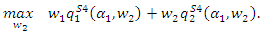 The first-order condition
The first-order condition 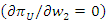 leads to
leads to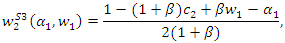 where superscript
where superscript  represents that the outcomes are in stage 3. Substituting this outcome into
represents that the outcomes are in stage 3. Substituting this outcome into 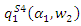 and
and 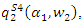 we have
we have 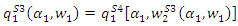 and
and 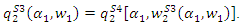 Substituting the above results into the profit of downstream firm
Substituting the above results into the profit of downstream firm 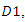 the maximization problem is
the maximization problem is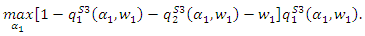 From the first-order condition
From the first-order condition 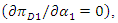 we have
we have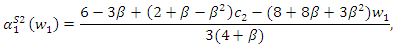 where superscript
where superscript 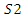 represents that the outcomes are in stage 2. Substituting this outcome into
represents that the outcomes are in stage 2. Substituting this outcome into 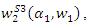
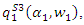 and
and 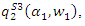 we have
we have 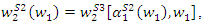
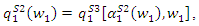 and
and 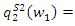
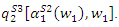 Substituting the above outcomes into the profit of upstream firm, the maximization problem is
Substituting the above outcomes into the profit of upstream firm, the maximization problem is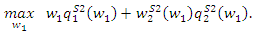 The first-order condition
The first-order condition 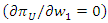 leads to
leads to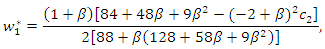 where superscript
where superscript  represents that the outcomes are in equilibrium. Summarizing the above results, we obtain the following proposition:Proposition 1. The equilibrium social welfare is
represents that the outcomes are in equilibrium. Summarizing the above results, we obtain the following proposition:Proposition 1. The equilibrium social welfare is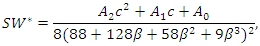 Where
Where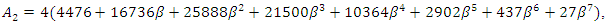
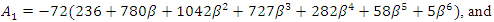
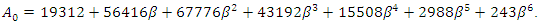 Differentiating
Differentiating  with respect to
with respect to 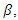 we have
we have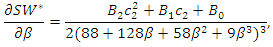 where
where 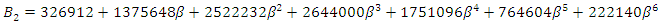
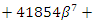
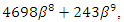
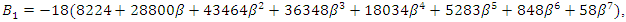 and
and 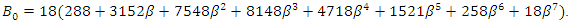 After a tedious calculation, we obtain the following proposition:Proposition 2. When we can freely choose a value of
After a tedious calculation, we obtain the following proposition:Proposition 2. When we can freely choose a value of 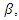 the equilibrium social welfare is minimized at the following
the equilibrium social welfare is minimized at the following 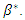
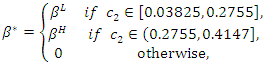 such that
such that 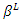 satisfies
satisfies 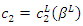 and
and 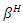 satisfies
satisfies 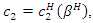 where
where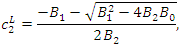
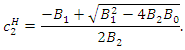 Proof. First, using the discriminant of the numerator for
Proof. First, using the discriminant of the numerator for 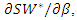 we show that the value of
we show that the value of 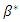 that minimizes
that minimizes 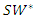 does not exist in
does not exist in 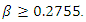 As the sign of denominator is positive, the sign of first derivative is the same as that of numerator. The numerator is the quadratic function of
As the sign of denominator is positive, the sign of first derivative is the same as that of numerator. The numerator is the quadratic function of 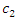 and the coefficient of
and the coefficient of 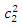 is positive
is positive 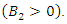 Then, if the sign of discriminant
Then, if the sign of discriminant 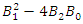 is non-positive, we will have
is non-positive, we will have 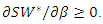 Numerically solving
Numerically solving 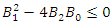 for
for 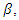 we have
we have 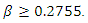 Hence, the value of
Hence, the value of 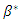 that minimizes
that minimizes 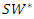 does not exist in
does not exist in 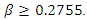 Next, we consider the case with
Next, we consider the case with 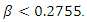 We will show that the equilibrium social welfare increases with
We will show that the equilibrium social welfare increases with 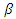 if
if 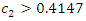 or
or 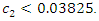 As the discriminant takes a positive value, we have two solutions:
As the discriminant takes a positive value, we have two solutions: 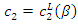 and
and 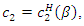 which satisfy
which satisfy 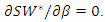 Solving
Solving 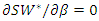 for
for 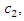 we have
we have
 Then, if
Then, if 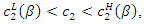 we have
we have 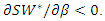 Here, from numerical calculation, we show that
Here, from numerical calculation, we show that 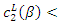
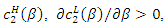 and
and 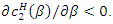 This result implies that the maximum value of
This result implies that the maximum value of 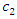 such that
such that 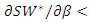
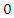 at some
at some 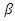 is derived from
is derived from 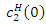 and the minimum value of
and the minimum value of 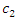 such that
such that 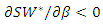 at some
at some 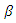 is obtained from
is obtained from 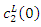 . That is,
. That is, 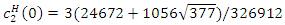
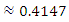 and
and 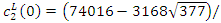
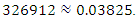 Hence, if
Hence, if 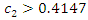 or
or 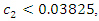 then the social welfare is minimized at
then the social welfare is minimized at 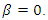 Finally, we consider the case with
Finally, we consider the case with 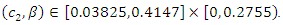 From numerical calculation, we have
From numerical calculation, we have 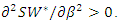 Hence,
Hence, 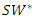 is a strictly convex function of
is a strictly convex function of 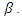 Then, the first-order condition
Then, the first-order condition 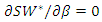 characterizes the value
characterizes the value 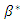 that minimizes
that minimizes 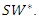 That is, by solving the first-order condition for
That is, by solving the first-order condition for 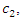 we have
we have 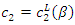 and
and 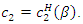 From the discriminant
From the discriminant 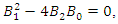 we have
we have 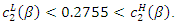 Then, given the value of
Then, given the value of 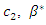 that minimizes equilibrium social welfare is implicitly determined as follows:
that minimizes equilibrium social welfare is implicitly determined as follows: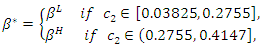 where
where 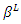 satisfies
satisfies 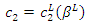 and
and 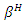 satisfies
satisfies 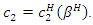 Therefore, we obtain the proposition.We can depict the result of Proposition 2 in Figure 1. In this figure, there are three regions. In the right area, as we have
Therefore, we obtain the proposition.We can depict the result of Proposition 2 in Figure 1. In this figure, there are three regions. In the right area, as we have 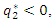 we omit this parameter range; in the shadow area, we have
we omit this parameter range; in the shadow area, we have 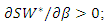 in the bottom area, we have
in the bottom area, we have 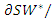
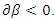 Hence, given
Hence, given 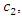 the boundary between the shadow and bottom areas determines
the boundary between the shadow and bottom areas determines 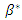 that leads to the minimum social welfare.
that leads to the minimum social welfare.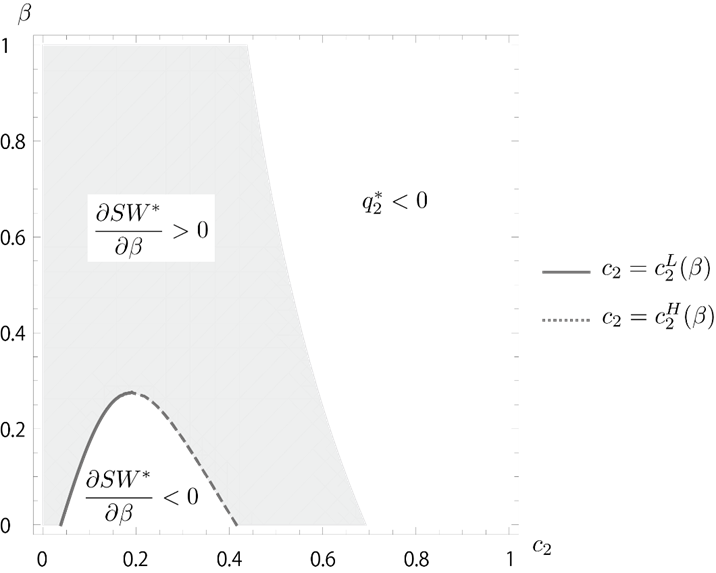 | Figure 1. Effect of 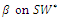 |
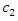 is in the range
is in the range  , the equilibrium social welfare is minimized neither at
, the equilibrium social welfare is minimized neither at 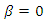 nor for
nor for 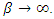 In other words, under the supply function competition except where
In other words, under the supply function competition except where 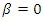 and
and 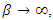 the equilibrium social welfare is smaller than those under Cournot and Bertrand competitions. Now, we explain an intuition behind Proposition 2. Since we consider the case of a sequential contract, follower
the equilibrium social welfare is smaller than those under Cournot and Bertrand competitions. Now, we explain an intuition behind Proposition 2. Since we consider the case of a sequential contract, follower 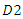 faces a residual demand after leader
faces a residual demand after leader 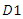 decides its output. Thus, the follower behaves less aggressively than in the case with a simultaneous contract. Then, to encourage the follower’s production, the upstream firm reduces the wholesale price for follower
decides its output. Thus, the follower behaves less aggressively than in the case with a simultaneous contract. Then, to encourage the follower’s production, the upstream firm reduces the wholesale price for follower 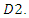 As leader
As leader 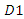 knows this action, it reduces its own output. If a decrease in
knows this action, it reduces its own output. If a decrease in 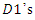 output dominates an increase in
output dominates an increase in 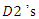 output, the total output reduces. Since in this case, an increase in
output, the total output reduces. Since in this case, an increase in 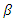 reduces social welfare and in the other case, the rise of
reduces social welfare and in the other case, the rise of 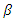 decreases the social welfare, there exists a positive
decreases the social welfare, there exists a positive 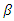 such that social welfare is minimized.
such that social welfare is minimized.4. Conclusions
- We consider the supply function competition structure in a vertical market with a sequential contract. We show that if the technological difference between downstream firms is moderate, an intermediate competition intensity yields the minimum social welfare. This result indicates that a competition policy that enhances competition, measured by the type of competition, is not desirable for society.
ACKNOWLEDGEMENTS
- I would like to express my cordial gratitude to Tomomichi Mizuno for his sincere encouragement, constructive and helpful comments, and in-depth discussion during the various stages of preparation. Needless to say, all remaining errors are mine.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML