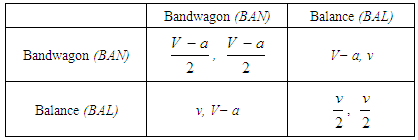-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2017; 6(2): 21-37
doi:10.5923/j.jgt.20170602.01

An Evolutionary Game Analysis of Balancing and Bandwagoning in Unipolar Systems
Serdar Ş. Güner
Department of International Relations, Bilkent University, Ankara, Turkey
Correspondence to: Serdar Ş. Güner, Department of International Relations, Bilkent University, Ankara, Turkey.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This article proposes a simple evolutionary game to analyze the stability of states’ balancing and bandwagoning behavior towards the sole superpower called the unipole. The trajectories leading to evolutionarily stable strategies (ESSs) demonstrate possible alignment paths given environmental constraints of unipolar systems and game rules. States are found to bandwagon with or balance against the unipole. They can also become divided adopting opposite alignment behaviors. The evolutionarily stable strategies imply alternative views of socialization and competition processes for structural realism, liberalism, and constructivism.
Keywords: Unipole, Balancer, Bandwagoner, Evolutionary Stable Strategy (ESS), Unipolar system, Unipolar environment
Cite this paper: Serdar Ş. Güner, An Evolutionary Game Analysis of Balancing and Bandwagoning in Unipolar Systems, Journal of Game Theory, Vol. 6 No. 2, 2017, pp. 21-37. doi: 10.5923/j.jgt.20170602.01.
Article Outline
1. Introduction
- A unipolar system contains a sole superpower called the unipole outranking all other states in terms of resource endowment and global operations ability. In essence, states in the second-tier are mostly concerned with the behavior of the unipole; their alignments constitute reactions to the superpower. This article develops an evolutionary game to investigate whether second-tier states choose to balance the unipole by forming a common front against it, or, inversely, align with the unipole corresponding to bandwagoning in a unipolar system. The game equilibria reveal whether states balance against or bandwagon with the unipole depending on the environment of the system.IR theory contains a rich vocabulary of evolutionary terms and conjectures but few evolutionary games [1]. The evolutionary game we propose models on-going interactions among states and differs from conventional games by being dynamic, that is, by explicitly dealing with how strategies change over time and by not requiring states to be rational [2-5].1 It pictures states as having a unique motive: increase resources. States co-exist in an environment where some policies they adopt toward the unipole enhance their resources more than others. They can commit mistakes but learn to select better strategies progressively. The policies evolve as states discover that some are more rewarding than others in increasing resource levels defined as fitness. They may find that balancing or bandwagoning is a better instrument as those states become fitter that balance or bandwagon with unipole. States are assumed to get fitter with increments of own resources [6]. The assumption implies that unipolar structures do not shape and shove states’ actions in a unique way with all becoming balancers as structural realism predicts. An overall opposition against the unipole does not arise automatically. Thus, balancing is not a one-way street in unipolar systems. The game implies that states’ actions can get similar while they err in imitating successful alignment modes. States can become divided as balancers and bandwagoners depending upon the unipolar environment as well or a single mutant bandwagoner can become successful and be imitated even if all states are balancers.2 The unipole then becomes the hegemon facing no opposition but enjoying supreme power in the system. We find also that states can bandwagon with a malign unipole or balance against a benign unipole. If they are distinct with respect to their individual traits, for example, their particular history with the unipole, then they can decide to become a bandwagoner or a balancer assuming alternative roles. States sharing the same individual traits are found not to adopt opposite alignment options. They all become either bandwagoners or balancers. The evolutionary trajectories leading to different game equilibria constitute socialization and competition processes. They indicate progressive similarity in states’ alignment policies toward the unipole and changes in fitness. The directional change of the processes varies depending on the environment of unipolar systems and on initial partitions of states adopting opposite alignment behaviors in some cases. Both processes pinpoint connections between structural realism, constructivism, and liberalism as the game equilibria are conventions, that is, outcomes of continuing practices.The remainder of the article is divided into six parts. The first briefly reviews theoretical and empirical analyses and conjectures about states’ behavior towards the unipole. The second motivates the stage game by stylizing alignment interactions in unipolar systems. The third presents the game and the equilibria different game variants imply. The fourth discusses theoretical implications. The fifth concludes. The appendix contains the proofs of the game equilibria.
2. Literature Review
- Theoretical ViewsBalance of power theory implies that states react against overwhelming power aiming to survive, therefore they are expected to balance against the unipole [7, 8].3 “If states wished to maximize power, they would join the stronger side, and we would see not balances forming but world hegemony forged. This does not happen because balancing, not bandwagoning, is the behavior induced by the system.” States strive to maintain their positions in the system first; they are not after power maximization. [9] States can align with the unipole to benefit from increased resources but they are able to assess that a resource improvement through bandwagoning is not accompanied with higher safety. Consequently, the most successful policy is balancing; bandwagoning policies are progressively eliminated and the superpower sooner or later faces counterbalancing efforts.Balance-of-threat theory implies that states adopt balancing if the unipole possesses a high amount of aggregate power, it is aggressive, it is endowed with offensive capabilities, and it is geographically proximate to others [10]. It is impossible for a unipole to be the neighbor of all remaining states; hence geographic factor in threat definition applies in well-defined neighborhoods [11, 12]. If the unipole harbors no aggressive intentions or it is geographically distant and endowed with defensive capabilities, then it can attract allies. States can also bandwagon with the unipole for protection against regional threats and the degree of order and public goods the unipole generates [13-15]. If the unipole is benevolent, that is, it uses its power with restraint, it engages merely in defensive measures and it adopts cooperative policies that benefit others, then there is no reason to oppose it. If states perceive the unipole as a benign actor engaged in such global strategies, then balancing against it becomes almost meaningless [16, 17]. Thus, states can bandwagon with a non-aggressive unipole that protects the status quo and opts for self-restraint [18].Empirical ViewsEmpirical literature identifies the United States as the unipole and focuses mostly on the U.S. behavior. The United States can adopt isolationism, engage selectively, pursue collective security, or aim at keeping its preponderance in the system [19]. Each strategy would imply different constraints for states affecting their actions. For example, states already believe, or can be led to believe, that the United States is a benign hegemon while it aims at preventing the rise of a peer competitor. The United States is therefore expected to meet with global support rather than opposition; “other states will not balance against the United States” [20]. Similarly, states will not balance against a non-aggressive United States they perceive as highly selective in its aggressiveness [21]. If the United States takes bellicose acts, states would react against what they perceive as efforts of global social engineering [22].States are also argued to be engaged in soft balancing, that is, they can use “nonmilitary tools to delay, frustrate, and undermine aggressive unilateral U.S. military policies” [23]. To illustrate, China, France, Germany, Japan, and Russia prefer not to challenge the United States directly by pooling military resources but take soft balancing measures. Nevertheless, soft balancing could later evolve into hard balancing as the response to an expansionist unipole is the formation of a global counter alliance [24]. Thus, soft balancing argument is similar to that of balance-of-threat but the measures are less conspicuous than formal alliances. The argument is indeed criticized as soft-balancing measures are nothing but “routine diplomatic friction” and “merely bargaining moves not directly aimed at reducing American hegemony” [25, 26].The cursory presentation of theoretical and empirical views on states’ alignment with respect to the unipole demonstrates that we need a framework simple enough to generate explanations and to discover connections between opposing arguments. The framework should be transparent in the sense that its assumptions are clearly stated so that one can follow how explanations are constructed. One may not assess how useful an assumption is before it is actually made [27]. “In science, it is more important that the conclusions be right than that the assumptions sound reasonable. The assumption of gravitational force seems totally unreasonable on the face of it, yet leads to correct conclusions” [28]. In our case, we can only speculate whether the conclusions are meaningful; not whether they are false or correct. Evolutionary processes take time; one cannot immediately assess empirical refutation or verification of conjectures the game implies.
3. Evolutionary Framework
- StatesStates are the players of the game. We assume that more resources a state controls, higher becomes its fitness and therefore its survival chances in a unipolar system. Higher resources are associated with higher likelihoods of independent existence, that is, success. Resourceful states are fitter and therefore successful. The assumption is more primitive than prominent classical realist views, because it is not associated either with metaphysical or religious characterization of man as evil and states’ aim to dominate others [29] or to increase power, that is, to improve “man’s control over the minds and actions of other men” [30].4 Survival comes before such motives. States must first subsist and possess resources.The assumption is in line with states’ aim to guarantee their survival: “I assume that states seek to ensure their survival…the aims of states may be endlessly varied; they may range from the ambition to conquer the world to the desire to be left alone. Survival is a prerequisite to achieving any goals that states may have, other than the goal of promoting their own disappearance as political entities” [31]. Hence, the assumption fixes states’ preferences and parallels structural realism with one difference, however: it does not ascribe multiple motives ranging from world domination to isolation.5ActionsTheoretical and empirical views concede that bandwagoning constitutes an alignment option available to states in a unipolar system. As to balancing, [32-34] argue that collective action problems hinder the formation of a joint front against the unipole. The resource gap between the unipole and prospective allies would complicate states’ coordination efforts. It is difficult for the allies to agree on how to share alliance costs and how much to contribute to their external balancing efforts. States that do not contribute would enjoy security benefits; therefore there are strong incentives to free ride in the system. States would avoid cooperation if their partners obtain higher benefits, as one’s increased resources can be later used to harm others hinting at the problem of whether states maximize absolute or relative gains in unipolar systems [35]. However, the debate over absolute and relative gains mistakenly takes effects for causes [36, 37]. One cannot simply assume that states maximize relative or absolute gains regardless situations states find themselves in: states’ concerns for absolute and relative gains vary depending upon systemic changes of strategic environments. Unipolar systems are structurally different from bipolar and multipolar systems, and, as we will later argue, not all unipolar systems possess equivalent environments.A more fundamental question is whether it is possible to form a global counter alliance against the unipole. If a state is the unipole and its resources are so large that they cannot be matched even if all states in the second-tier combine their resources, the global front does not constitute any counterpoise. Hence, external balancing in unipolar systems is almost impossible. The question of “who will gain more?” then loses its meaning; relative gain concerns dissipate with no prospect of cooperation against the unipole--revived perhaps in regional interactions. Consequently, states can choose either bandwagoning or internal balancing.6 States can improve their resource levels by domestic efforts such as allocations of more resources to defense, changes in military doctrines in targeting the unipole even though the unipole’s level of resources is out of reach [38].Unipolar EnvironmentsWe assume that two parameters make up the environment of a unipolar system: the behavior of the unipole and the distribution of resources across states. Bandwagoning and internal balancing generate different magnitudes of fitness enhancements depending upon the environment. Bandwagoners essentially obtain unipole’s protection and technology transfers. The unipolar actor’s backing and help in local security problems and improvement of defense levels by direct military and economic aid bolster bandwagoners’ domestic resources in a complex fashion. Yet bandwagoning is costly for two reasons. First, bandwagoners lose their freedom of action. An alignment with a major power provides a large increase in security at the cost of limited range of foreign policy options [39, 40]. The interests of states and the unipole would not be concordant in an issue. Second, bandwagoners face the prospect of sharing the costs of unipolar actor’s interventions around the globe [41]. Thus, bandwagoners’ resource improvements and costs depend upon the unipole’s type.The unipole is assumed to be either benign, so that it voluntarily constrains its power, or malign, that is, it pursues its own ideals about the international system [42-44].7 A benign unipole acts in such a way that it does not threaten states: it delimits own actions in managing international politics, it does not take advantage of its superior position, and promotes actions and institutions for joint gains. In contrast, a malign unipole intervenes around the globe and these operations threaten states. It takes advantage of its superior position by putting no limits on own actions. It does not necessarily promote actions and institutions for joint gains. The unipole’s global management therefore determines the magnitude of bandwagoners’ fitness.The distribution of resources across states in turn determines balancers’ resource improvement: Balancers draw upon own resources. Higher states’ levels of development, technology, and capabilities, higher become their resource gains through internal balancing efforts. Internal balancing is however less resource enriching than bandwagoning: no state can attain the same quantity and quality of resources through domestic efforts as those resources and assistance the unipole can provide. The unipole’s backing and help are assumed to be more effective in bolstering resources. Balancers enjoy although one advantage: they are not subject to the cost of bandwagoning by definition. Thus, bandwagoners’ and balancers’ resource improvements can be high or low, the cost of bandwagoning can also be high, low, or even zero. Each combination implies a different class of unipolar environment. There can be a unipolar system where the unipole is benign and therefore helps states in resolution of local conflicts and improvement of defense levels through its direct military and economic aid. Bandwagoners then benefit from high enhancements in resource levels. They would also suffer from negligible costs provided that the benign unipole does not conduct global interventions asking for states’ assistance and it does not delimit bandwagoners’ range of foreign policy choices. Suppose also that states benefit from high levels of development, technology, and capabilities in the system. Such an environment is in sharp contrast with the one where a malign unipole forces states to act in its favor and to pursue policies against their national interests, and states have a low level of development, technology, and capabilities. Therefore, unipolar systems are structurally identical but can be environmentally different. Unipolar environments produce constraints altering states’ resource improvements through balancing and bandwagoning. Foreign Policy ModelStates are assumed to emulate those strategies that improve fitness. Balancing and bandwagoning are opposed behaviors but they are motivated by the same goal: achieve a higher amount of resources and get fitter. States are not “programmed” to bandwagon with the unipole or internally balance against it either. They gradually learn to adapt to the environment [45]. Adherents of alignments that are poor responses to unipolar environments are eventually overwhelmed by adherents of those that bolster fitness. We therefore have to explain states’ particular actions. In other words, the evolutionary game necessitates a model of foreign policy making. We start by assuming that states are not black boxes. The leaders, elites, and organizations related to foreign policy make up the state, and, they do not have enough information about the environment [46, 47]. Leaders and organizations make mistakes due to routines, limited capacities of processing information, and misperceptions which generate inconsistencies in reaching collective decisions [48, 49]. Elites can misperceive the unipole’s intentions and behavior and each other’s preferences about whether balancing or bandwagoning is a better tool to improve fitness. Moreover, organizations’ standard operating procedures create routines which are not optimal in assessment and comparisons of resources. As a result, states do not adopt the most successful action instantly when they compare resource levels. Nevertheless, they find that either balancing or bandwagoning performs better through lengthy trial-and-error processes by adapting to successful alignment trends in the system.To illustrate, suppose that the leaders and bureaucrats of various organizations of a state discuss and negotiate among themselves what behavior to adopt with respect to the unipole. In doing so, they compare the action and the resource levels of other states with theirs. They discuss and decide through internal politicking and controversies whether bandwagoning or internal balancing is a better tool to raise the level of fitness. They can however commit a mistake by adopting internal balancing while a sensible majority of states opt for bandwagoning and increase their resource levels, or adopting to bandwagon with the unipole while a sizable portion of states improve survival chances through internal balancing. They might also assess that one policy is better than the other yet they may repeat the mistake without changing state’s foreign policy. Nevertheless, unfit actions become sooner or later replaced by fitter ones so that the state survives better in the system [50]. Adaptation to the environment takes time.EquilibriaA strategy becomes evolutionarily stable if all states ultimately adopt it and no different strategy can replace it. An evolutionarily stable strategy (ESS) is the state of strategy distribution that cannot be “invaded” by alternative actions. If, for example, all states are bandwagoners as bandwagoning is the ESS, then if some states adopt balancing, they obtain a lower amount of fitness and revert to bandwagoning. In general terms, mutants, that is, small minorities of states employing deviant actions eventually disappear and finally conform to the ESS. The disappearance of mutants does not correspond to states vanishing from the international scene but to the conversion of their actions into successful ones.States’ behavior towards the unipole can approach some stability over time, as fitter strategies progressively become prevalent and other strategies become extinct.8 If bandwagoning provides a higher resource level depending upon the prevalent bandwagoning-balancing configuration in the population, a greater number of states would align with unipole. Nevertheless, if the rest of the population chooses bandwagoning, a state may be able to reap benefits if it chooses internal balancing. Similarly, if the rest of the population balance against the unipole, then a state may find that to bandwagon with the unipole is the fitter strategy. Hence, it does not mean that a prevailing strategy is the ESS and the one that produces higher fitness. States’ actions become adapted to the unipolar environment over the long haul. States are after augmenting resources but they are boundedly rational, as elites err in resource assessments and whether balancing or bandwagoning is a better policy to improve fitness. Consequently, the evolution of states’ behavior towards the unipole depends upon the dispersal of policies that improve fitness while the environment does not change. If bandwagoning with the unipole brings more resources, then more states adopt it; otherwise they become balancers. Successful bandwagoning breeds bandwagoning and successful balancing breeds balancing.
4. The Game
- The game assumes that states repeatedly compare respective levels of fitness. We first assume that the comparisons of fitness and actions are assumed to take place randomly: the probability that a state’s matching with a bandwagoner or a balancer equals the proportion of bandwagoners and balancers, respectively. The assumption points out to some indifference of elites and organizations involved in foreign policy making who randomly pick a state, say state X, and compare their own alignment efforts and resulting resource improvements with those of state X. Nevertheless, the decision makers might not be that indifferent towards various states. They might rather be interested in how a specific state is performing in the system. Therefore randomness assumption can be relaxed. We accordingly assume that a state can also be matched at a higher probability with those that share its alignment action. This amounts to assortative matching [51]. Some states, for example, would be less inclined to bandwagon with the unipole for some historical, internal political or some other reasons. Once a state cannot easily become a bandwagoner, then the assessment of how those allies of the unipole fare in the system becomes useless. Thus, it is more likely that a bandwagoner (balancer) compares its fitness with a fellow bandwagoner (balancer). The assumption then implies that balancers and bandwagoners can be quite differentiated on the basis of various unipolar environments. For example, if balancers’ resource and technology levels are low, then they are disfavored compared to bandwagoners during the evolution of actions towards the unipole.We also differentiate between two types of populations. First, we assume that the population of states is homogeneous, that is, states’ roles in the evolutionary process remain the same: they are not strategically different from each other. Second, we assume that the population of states is not homogeneous. States can condition their alignment choices on their individual traits, for example, their histories of relationship with the unipole, regime types, or any other feature. States then become strategically distinct when they decide to become a bandwagoner or a balancer assuming alternative roles. We first assume that the population of states is either homogeneous or non-homogeneous and study evolutionary dynamics under random matching in the variant 1 (homogeneous population-random matching) and the variant 2 (non-homogeneous population-random matching). We later extend the analysis by assuming a homogeneous population and assortative matching in the variant 3.Let V, v, a respectively denote resources available to bandwagoners and balancers and the cost of bandwagoning in a unipolar environment. They are assumed to satisfy conditions of V > 0, v > 0, V > v, and a ≥ 0, V ≥ a. The parameters can change across environments. If V drops, it still exceeds v, the cost of bandwagoning varies between V at its maximum and 0 at its minimum, and, v never attains 0, that is, internal balancing always yields some amount of fitness. States in the second-tier occupy identical positions with respect to each other and the unipole. Unipolar systems produce structural symmetry. Therefore, if two states adopt bandwagoning, their resource enhancements will be equal:
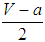 . Similarly, two balancers obtain
. Similarly, two balancers obtain 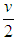 . If they adopt opposite alignment policies, their fitness improvements become asymmetric. The state that aligns with unipole obtains V − a, and the balancer obtains the whole resource v. Payoffs in the game below indicate states’ fitness depending on their alignment policies toward the unipole.
. If they adopt opposite alignment policies, their fitness improvements become asymmetric. The state that aligns with unipole obtains V − a, and the balancer obtains the whole resource v. Payoffs in the game below indicate states’ fitness depending on their alignment policies toward the unipole.
|
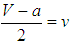 , then
, then 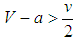 . Therefore, if bandwagoners and balancers do equally good among bandwagoners, then bandwagoners must be more successful than balancers among balancers for bandwagoning to be the ESS. If the Nash equilibrium is strict, that is, U(BAN, BAN) > U(BAL, BAN), then the condition U(BAN, BAL) > U(BAL, BAL) is satisfied automatically. Bandwagoners obtain a strictly higher amount of resources than balancers among bandwagoners and bandwagoning becomes established as an evolutionarily stable strategy among states. As a result, BAN is the ESS provided that
. Therefore, if bandwagoners and balancers do equally good among bandwagoners, then bandwagoners must be more successful than balancers among balancers for bandwagoning to be the ESS. If the Nash equilibrium is strict, that is, U(BAN, BAN) > U(BAL, BAN), then the condition U(BAN, BAL) > U(BAL, BAL) is satisfied automatically. Bandwagoners obtain a strictly higher amount of resources than balancers among bandwagoners and bandwagoning becomes established as an evolutionarily stable strategy among states. As a result, BAN is the ESS provided that 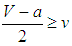 . Similarly, if U(BAL, BAL) = U(BAN, BAL) and U(BAL, BAN) > U(BAN, BAN), or, simply, if U(BAL, BAL) > U(BAN, BAL), then BAL is the ESS. The ESS become all states’ balancing against the unipolar actor if balancers and bandwagoners perform equally well among balancers but balancers fare better than bandwagoners among bandwagoners or if balancers are more successful than bandwagoners among balancers. Thus, we need either
. Similarly, if U(BAL, BAL) = U(BAN, BAL) and U(BAL, BAN) > U(BAN, BAN), or, simply, if U(BAL, BAL) > U(BAN, BAL), then BAL is the ESS. The ESS become all states’ balancing against the unipolar actor if balancers and bandwagoners perform equally well among balancers but balancers fare better than bandwagoners among bandwagoners or if balancers are more successful than bandwagoners among balancers. Thus, we need either 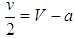 and
and 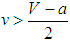 , or, simply,
, or, simply, 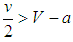 , for BAL to be an evolutionarily stable strategy. If
, for BAL to be an evolutionarily stable strategy. If 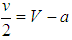 , then
, then 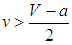 . Consequently, BAL is the ESS provided that
. Consequently, BAL is the ESS provided that 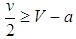 .No symmetric Nash equilibrium and therefore no pure ESS exist if
.No symmetric Nash equilibrium and therefore no pure ESS exist if 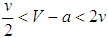 . The unique symmetric Nash equilibrium arises in mixed strategies with
. The unique symmetric Nash equilibrium arises in mixed strategies with 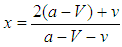 and
and 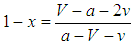 , where x is the fraction of bandwagoners and
, where x is the fraction of bandwagoners and 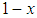 is the fraction of balancers in the population.9 The division of states as bandwagoners and balancers is called a polymorphic equilibrium.To see how bandwagoning and balancing evolve over time, we have to consider the expected resource improvements from each strategy given that some states are bandwagoners and some others are balancers. Let f(BAN) denote the fitness of bandwagoners and f(BAL) the fitness of balancers, x denote the fraction of bandwagoners and
is the fraction of balancers in the population.9 The division of states as bandwagoners and balancers is called a polymorphic equilibrium.To see how bandwagoning and balancing evolve over time, we have to consider the expected resource improvements from each strategy given that some states are bandwagoners and some others are balancers. Let f(BAN) denote the fitness of bandwagoners and f(BAL) the fitness of balancers, x denote the fraction of bandwagoners and 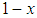 the fraction of balancers in the population. From Table 1, it follows that:
the fraction of balancers in the population. From Table 1, it follows that: 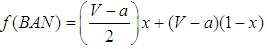 | (1) |
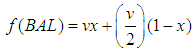 | (2) |
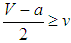 , so that
, so that 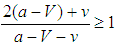 , all states become bandwagoners, that is,
, all states become bandwagoners, that is, 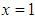 ;
; | Figure 1. Homogeneous Population Monomorphic Equilibrium |
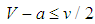 , so that
, so that 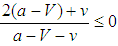 , all states become balancers, that is, x = 0;
, all states become balancers, that is, x = 0; | Figure 2. Homogeneous Population Monomorphic Equilibrium |
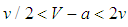 , so that
, so that 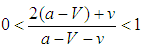 , states become divided as bandwagoners and balancers.
, states become divided as bandwagoners and balancers. | Figure 3. Homogeneous Population Polymorphic Equilibrium |
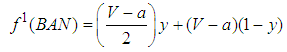 | (3) |
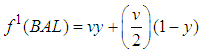 | (4) |
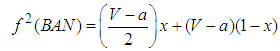 | (5) |
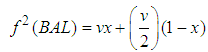 | (6) |
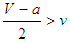 and
and 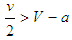 , respectively. The figure 6 shows the evolution of strategies when
, respectively. The figure 6 shows the evolution of strategies when 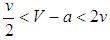 .In the figure 4, all types finally jump in the bandwagon, thus all trajectories end up in the state of
.In the figure 4, all types finally jump in the bandwagon, thus all trajectories end up in the state of  whatever is the initial composition of types of bandwagoners and balancers the population. Both type of states bandwagon with the unipole ultimately. Similarly, all trajectories end up in the state of
whatever is the initial composition of types of bandwagoners and balancers the population. Both type of states bandwagon with the unipole ultimately. Similarly, all trajectories end up in the state of 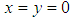 in the figure 5 regardless of initial conditions; all types choose balancing.
in the figure 5 regardless of initial conditions; all types choose balancing.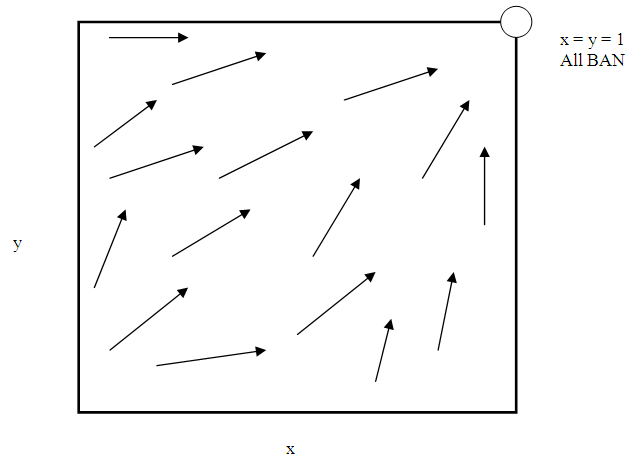 | Figure 4. Non-homogeneous Population, Monomorphic Equilibrium |
 | Figure 5. Non-homogeneous Population, Monomorphic Equilibrium |
 if
if  but toward
but toward  if
if  . If type-1 bandwagoners are more numerous than type-2 bandwagoners at the start, all type-1 states finally bandwagon with but all type-2 states balance against the unipole. No type-1 balancers or type-2 bandwagoners survive. The equilibrium is reversed when type-2 bandwagoners are more numerous than type-1 bandwagoners. The evolution of actions is stabilized with all type-2 states but no type-1 state becoming bandwagoners. Similarly, type-2 balancers and type-1 bandwagoners get extinct. Hence, either all type-1 states or type-2 states choose bandwagoning ultimately; it is impossible that all states bandwagon with or balance against the unipole regardless their type.
. If type-1 bandwagoners are more numerous than type-2 bandwagoners at the start, all type-1 states finally bandwagon with but all type-2 states balance against the unipole. No type-1 balancers or type-2 bandwagoners survive. The equilibrium is reversed when type-2 bandwagoners are more numerous than type-1 bandwagoners. The evolution of actions is stabilized with all type-2 states but no type-1 state becoming bandwagoners. Similarly, type-2 balancers and type-1 bandwagoners get extinct. Hence, either all type-1 states or type-2 states choose bandwagoning ultimately; it is impossible that all states bandwagon with or balance against the unipole regardless their type. 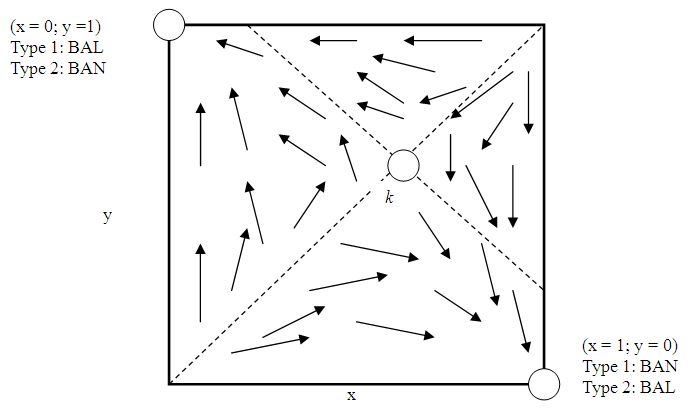 | Figure 6. Non-homogeneous Population Polymorphic Equilibrium |
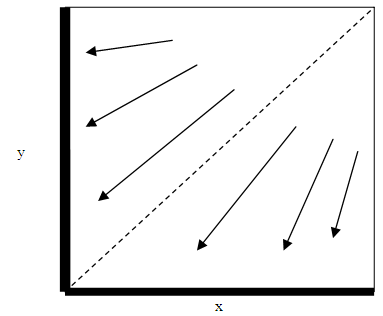
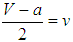 and initially type-1 bandwagoners are more numerous than type-2 bandwagoners, the evolution of actions is stabilized with all type-1 states becoming bandwagoners but type-2 states becoming divided into factions of balancers and bandwagoners. Otherwise, if type-2 bandwagoners are initially more numerous than type-1 bandwagoners, then all type-2 states switch to bandwagoning and the type-1 states become divided as balancers and bandwagoners.If
and initially type-1 bandwagoners are more numerous than type-2 bandwagoners, the evolution of actions is stabilized with all type-1 states becoming bandwagoners but type-2 states becoming divided into factions of balancers and bandwagoners. Otherwise, if type-2 bandwagoners are initially more numerous than type-1 bandwagoners, then all type-2 states switch to bandwagoning and the type-1 states become divided as balancers and bandwagoners.If 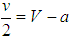 and type-1 bandwagoners are more numerous than type-2 bandwagoners, all type-2 states become balancers and type-1 states becomes divided. Finally, if type-2 bandwagoners are more numerous than type-1 bandwagoners, all type-1 states become balancers and the type-2 states in turn become divided. The bold lines in the figures 7 and 8 indicate that states in one type of population all adopt the same action towards the unipole while states of the other type become divided. For example, in the figure above, if the number of Type-1 bandwagoners is greater than Type-2 bandwagoners, no Type-2 bandwagoner survives but Type-1 states become partitioned as balancers and bandwagoners. We qualify such apportionments as hybrid equilibria.
and type-1 bandwagoners are more numerous than type-2 bandwagoners, all type-2 states become balancers and type-1 states becomes divided. Finally, if type-2 bandwagoners are more numerous than type-1 bandwagoners, all type-1 states become balancers and the type-2 states in turn become divided. The bold lines in the figures 7 and 8 indicate that states in one type of population all adopt the same action towards the unipole while states of the other type become divided. For example, in the figure above, if the number of Type-1 bandwagoners is greater than Type-2 bandwagoners, no Type-2 bandwagoner survives but Type-1 states become partitioned as balancers and bandwagoners. We qualify such apportionments as hybrid equilibria.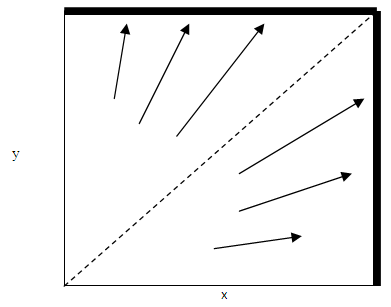 | Figure 7. Non-homogeneous Population Hybrid Equilibrium |
 | Figure 8. Non-homogeneous Population Hybrid Equilibrium |
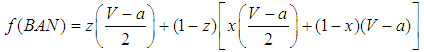 | (7) |
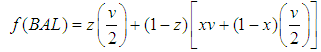 | (8) |
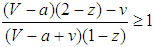 , all states become bandwagoners;ii) If
, all states become bandwagoners;ii) If 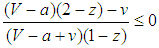 , all states become balancers;iii) If
, all states become balancers;iii) If 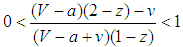 , states become divided as bandwagoners and balancers.The cases imply conditions on the probability z. If
, states become divided as bandwagoners and balancers.The cases imply conditions on the probability z. If 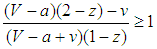 , all states become bandwagoners provided that
, all states become bandwagoners provided that 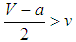 for all z such that 0<z<1. This result corresponds to the case under random matching. In addition, if
for all z such that 0<z<1. This result corresponds to the case under random matching. In addition, if 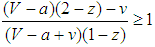 , all states become bandwagoners provided that if
, all states become bandwagoners provided that if 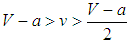 and
and 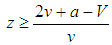 where
where 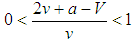 . Similarly, if
. Similarly, if 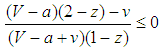 and
and 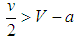 , all states become balancers for all z, 0<z<1, as in the case of random matching. It is also possible that all states become balancers if
, all states become balancers for all z, 0<z<1, as in the case of random matching. It is also possible that all states become balancers if 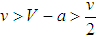 and
and 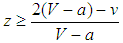 where
where 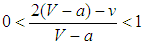 .Finally, if
.Finally, if 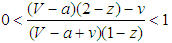 and
and 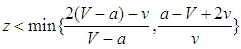 a polymorphic equilibrium is obtained. The minimum threshold is
a polymorphic equilibrium is obtained. The minimum threshold is 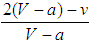 if
if 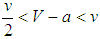 , and, it is
, and, it is 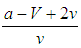 if
if 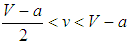 . Thus, states become partitioned into balancers and bandwagoners under assortative matching if either
. Thus, states become partitioned into balancers and bandwagoners under assortative matching if either 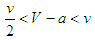 or
or 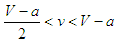 . The environments differ from
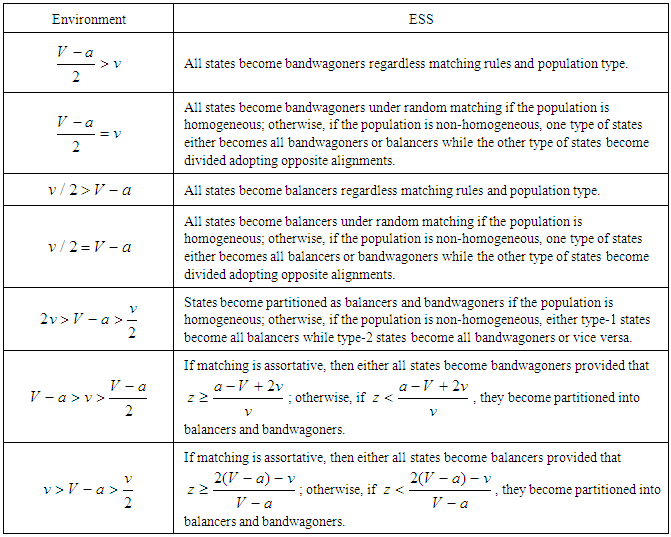
. The environments differ from 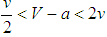 , the one where a polymorphic equilibrium results under random matching. In general, compared to random matching, the assumption of assortative matching reveals the importance of additional unipolar environments allowing additional interpretations and implications. The table below summarizes all findings.
, the one where a polymorphic equilibrium results under random matching. In general, compared to random matching, the assumption of assortative matching reveals the importance of additional unipolar environments allowing additional interpretations and implications. The table below summarizes all findings.
|
5. Implications
- What does the game imply for unipolar systems? How does the model help us in generating explanations of opposite forms of alignment toward the unipole? We answer these questions by classifying the equilibria with respect to outcomes and processes. Some outcomes are conspicuous as no balancers or bandwagoners survive through evolutionary processes indicating an evolving similarity in actions. All states’ alignment with the unipole corresponds to the unipole’s absolute dominance and therefore the unipole’s hegemony in the system; otherwise, a global resistance through overall internal balancing emerges against the unipole. The progressive similarities in actions and possible behavioral dynamic bifurcations such as the division of states as balancers and bandwagoners generate alternative interpretations of socialization and competition processes which are of interest to structural realism, liberalism, and constructivism.11Hegemony Versus UnipolarityUnipolar and hegemonic systems are similar as they all include one globally dominant state but boundaries between them remain fuzzy. “Hegemony is a concept that is widely used, but it is rarely defined with any degree of precision” [55]. A distinction can be made by proposing that hegemony refers to power relations unlike unipolarity. The hegemon is “the state with control over raw materials, control over resources of capital, and competitive advantages in the production of highly valued goods“ [56]; a “single powerful state that controls or dominates lesser states in the system” [57]. Thus, a hegemon is omnipotent: it enjoys an absolute ability to conduct policies it prefers and globally dictates them. The game assumes that the unipole is the state possessing more resources than the sum of resources all other states control in the system. However, the unipole’s extreme resource superiority does not automatically translate into absolute power, therefore, a hegemon. The control over resources is distinct from the control over actors [58]. The unipole is, in a sense, the hegemon in terms of resources but not in terms of power. The game implies a relationship between unipolarity and hegemony: if bandwagoning is the ESS, so that all states ultimately align with the unipole, the unipole faces no single opposition and it transforms into a hegemon. Hence, if the benefits are high and the cost of alignment with the unipole is sufficiently low, so that the environment is
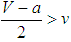 , then the unipolar system transforms into a hegemonic one whether states compare their resources randomly or assortatively. A reason of bandwagoning is indeed argued to be secondary state elites’ “subjective awareness” of benefits the hegemonic order generates [59, 60]. If bandwagoners obtain strictly higher resources among themselves than a balancer among them, they become successful and balancing is ultimately eradicated. States get fitter while the system evolves into a hegemonic one. The bandwagoning of all with the unipole becomes stable; if some states deviate to balancing, evolutionary dynamics drives the population of states back to the original equilibrium state. Assortative matching refines the hegemony condition by revealing the environment of
, then the unipolar system transforms into a hegemonic one whether states compare their resources randomly or assortatively. A reason of bandwagoning is indeed argued to be secondary state elites’ “subjective awareness” of benefits the hegemonic order generates [59, 60]. If bandwagoners obtain strictly higher resources among themselves than a balancer among them, they become successful and balancing is ultimately eradicated. States get fitter while the system evolves into a hegemonic one. The bandwagoning of all with the unipole becomes stable; if some states deviate to balancing, evolutionary dynamics drives the population of states back to the original equilibrium state. Assortative matching refines the hegemony condition by revealing the environment of 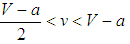 conducive to hegemony if
conducive to hegemony if 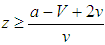 . A numerical example is helpful here. Suppose that the maximum value of V is 1 and the alignment cost a varies between 1 at maximum and 0 at minimum. We have V > v > 0 by assumption. If V = 1, a = 0.6, v = 0.3, so that the environment is
. A numerical example is helpful here. Suppose that the maximum value of V is 1 and the alignment cost a varies between 1 at maximum and 0 at minimum. We have V > v > 0 by assumption. If V = 1, a = 0.6, v = 0.3, so that the environment is 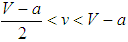 and z ≥ 0.66, so that at least two-third of states compare resources only with similarly aligned states, the unipolar system transforms into a hegemonic one. The result holds even if there is a unique bandwagoner while the cost of alignment with the unipole is twice as much the resource available to balancers. However, if the cost increases and attains, say, the value of 0.7, the unipole’s hegemony becomes impossible. Thus, compared to random encounters, assortative comparisons are more likely to lead to hegemony.Benign Versus Malign UnipolarityStates’ alignment with and against a unipole can find equal theoretical support assuming that are rational and react against power or images of it [61]. The balance-of-threat theory implies that states would oppose against a unipole which constitutes a global threat; otherwise if the unipole is benign, states would bandwagon with it to augment resources and to improve security. Are there any chances that a benign unipole becomes the hegemon?The cost of bandwagoning with the benign unipole can be zero or almost zero. Consequently, if the unipole is benign, so that
and z ≥ 0.66, so that at least two-third of states compare resources only with similarly aligned states, the unipolar system transforms into a hegemonic one. The result holds even if there is a unique bandwagoner while the cost of alignment with the unipole is twice as much the resource available to balancers. However, if the cost increases and attains, say, the value of 0.7, the unipole’s hegemony becomes impossible. Thus, compared to random encounters, assortative comparisons are more likely to lead to hegemony.Benign Versus Malign UnipolarityStates’ alignment with and against a unipole can find equal theoretical support assuming that are rational and react against power or images of it [61]. The balance-of-threat theory implies that states would oppose against a unipole which constitutes a global threat; otherwise if the unipole is benign, states would bandwagon with it to augment resources and to improve security. Are there any chances that a benign unipole becomes the hegemon?The cost of bandwagoning with the benign unipole can be zero or almost zero. Consequently, if the unipole is benign, so that 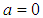 or
or 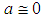 , the environment
, the environment 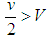 becomes impossible by assumption:
becomes impossible by assumption: 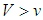 . The benign unipole never faces global balancing efforts. Nevertheless, if states’ technology, development, and resource levels are relatively high so that v satisfies the condition
. The benign unipole never faces global balancing efforts. Nevertheless, if states’ technology, development, and resource levels are relatively high so that v satisfies the condition 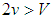 , it is possible that balancers multiply if states randomly compare their performances in the environments
, it is possible that balancers multiply if states randomly compare their performances in the environments 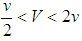 and
and 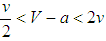 . Similarly, a benign unipole cannot become a hegemon under assortative matching if the environment is
. Similarly, a benign unipole cannot become a hegemon under assortative matching if the environment is 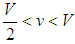 and
and 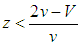 as some states become bandwagoners but some balancers. If, for example, V = 1, v = 0.6, and a = 0, some states become bandwagoners and some others balancers provided that less than one-third of the states compares their resource levels with those that are similarly aligned. The unipolar system evolves into a hybrid one where it is better to bandwagon with the unipole when balancers make up the majority and it is better to balance against the unipole when bandwagoners are more numerous than balancers in the non-homogeneous population under random matching.12 The competition process does not single out a unique successful strategy to increase fitness. States are ultimately partitioned as balancers and bandwagoners. Therefore, a zero or almost zero cost of bandwagoning is not sufficient for a benign unipole to become a hegemon. If the unipole is malign, that is, its interventions threaten states, it takes advantage of its superior position by putting no limits on own actions and does not necessarily promote actions and institutions for joint gains. The resource of bandwagoning would then be considerably cut down by a high value of a. Will states balance against the malign unipole? The answer is again negative. If the cost of bandwagoning is so high that the unipolar system environment is
as some states become bandwagoners but some balancers. If, for example, V = 1, v = 0.6, and a = 0, some states become bandwagoners and some others balancers provided that less than one-third of the states compares their resource levels with those that are similarly aligned. The unipolar system evolves into a hybrid one where it is better to bandwagon with the unipole when balancers make up the majority and it is better to balance against the unipole when bandwagoners are more numerous than balancers in the non-homogeneous population under random matching.12 The competition process does not single out a unique successful strategy to increase fitness. States are ultimately partitioned as balancers and bandwagoners. Therefore, a zero or almost zero cost of bandwagoning is not sufficient for a benign unipole to become a hegemon. If the unipole is malign, that is, its interventions threaten states, it takes advantage of its superior position by putting no limits on own actions and does not necessarily promote actions and institutions for joint gains. The resource of bandwagoning would then be considerably cut down by a high value of a. Will states balance against the malign unipole? The answer is again negative. If the cost of bandwagoning is so high that the unipolar system environment is 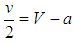 , that is, half of balancers resource becomes equal to the resource a bandwagoner obtains matched with a balancer, a single bandwagoner can disturb the stability of global balance against the malign unipole. And if
, that is, half of balancers resource becomes equal to the resource a bandwagoner obtains matched with a balancer, a single bandwagoner can disturb the stability of global balance against the malign unipole. And if 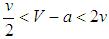 under random matching, or if
under random matching, or if 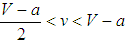 and
and 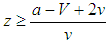 under assortative matching, some states would learn to align with a malign unipole. These cases of polymorphic equilibria confirm that opportunities of gain, even small, explain alignments with threats [61]. Thus, states as adaptive learners can become bandwagoners similar to those states that decide to align with a threatening unipole to maximize expected payoffs.Socialization and CompetitionStructural RealismStructural realism contains strong evolutionary arguments and is closely linked with social Darwinism [62].13 The theory outlines an evolutionary framework without specifying the population of states subject to evolution, the environment, and the selection and success criteria in international systems [63]. States, not assumed to be necessarily rational, emulate successful practices through socialization and competition processes which depend more upon actions than preferences.14 Socialization is defined as the process through which states are affected back by their own interactions. Competition is the process through which states opt for the most successful practice [64]. We adopt the same definition of competition. We define socialization as the process of change in states’ fitness.15 Both processes indicate how structures of international systems shape and shove state behavior and imply progressive similarity in evolving policies and resources. We first observe that each trajectory leading to evolutionarily stable strategies in the figures describe socialization and competition in unipolar systems. States’ adoption of specific actions affects their fitness. States get progressively resourceful as the actions evolve in the direction of the ESSs. If, for example, bandwagoning is the ESS as the unipolar environment is
under assortative matching, some states would learn to align with a malign unipole. These cases of polymorphic equilibria confirm that opportunities of gain, even small, explain alignments with threats [61]. Thus, states as adaptive learners can become bandwagoners similar to those states that decide to align with a threatening unipole to maximize expected payoffs.Socialization and CompetitionStructural RealismStructural realism contains strong evolutionary arguments and is closely linked with social Darwinism [62].13 The theory outlines an evolutionary framework without specifying the population of states subject to evolution, the environment, and the selection and success criteria in international systems [63]. States, not assumed to be necessarily rational, emulate successful practices through socialization and competition processes which depend more upon actions than preferences.14 Socialization is defined as the process through which states are affected back by their own interactions. Competition is the process through which states opt for the most successful practice [64]. We adopt the same definition of competition. We define socialization as the process of change in states’ fitness.15 Both processes indicate how structures of international systems shape and shove state behavior and imply progressive similarity in evolving policies and resources. We first observe that each trajectory leading to evolutionarily stable strategies in the figures describe socialization and competition in unipolar systems. States’ adoption of specific actions affects their fitness. States get progressively resourceful as the actions evolve in the direction of the ESSs. If, for example, bandwagoning is the ESS as the unipolar environment is 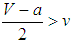 , socialization constitutes a dynamic process of states getting more resourceful. The fitness of bandwagoners improves as balancers always obtain lower resources among them.Structural realism indicates that states are expected to balance against the unipole: balancing is the most successful practice as states are watchful about relative gains. In contrast, the ESS imply that the processes are not unique, as there are infinitely many trajectories leading to overall balancing or bandwagoning depending upon initial conditions. The polymorphic equilibria imply that competition among states for more resources can establish two opposite but successful behaviors. Hence, the most successful alignment policy can be bandwagoning, balancing, or a mixture of them. Competition is not a one-way street.LiberalismPreferences constitute the central liberal variable and stem from various sources ranging from societal ideas and interests to institutions [65]. Liberalism does not either necessitate that states are unitary or rational similar to the foreign policy model assumptions. The game demonstrates that not elites’ preferences but the dispersal of alignment actions in the system drives evolutionary dynamics. States’ adjust their alignment policies toward the unipole through elites’ learning processes under errors and mistakes which can be related to domestic constraints such as the trade-off between domestic and international needs, that is, the “guns or butter” problem.A connection between elites, socialization, and competition processes for hegemonic systems is indeed proposed [66]. States become socialized as their elites accept values and norms the hegemon advances. National leaders progressively accept the hegemon’s norms and values, and, as a consequence, variations in policies towards the hegemon are reduced. It is argued that secondary states’ elites’ internalization of hegemon’s value orientations have nothing to do with forces at system-level ruling structure’s effect upon socialization out and that there are “meager analytic tools to understand the mechanisms and conditions” of socialization [67]. The game proposes mechanisms and conditions for socialization and demonstrates that elites’ learning processes make up forces at system level given the distribution of alignment actions. Any ESS of the game derives from elites’ learning processes and describes policy dispersal across states. An alignment policy becomes evolutionarily stable as system environments set up unipolar constraints affecting elites’ learning (including organizations’ operations). Thus, structure’s effect upon socialization can matter. It is possible that elites’ learning and organizations’ operations imply mistakes, for example, a state may adopt balancing while bandwagoning produce higher resource amounts, or, making no mistakes and achieving a boost in their state’s domestic resources. In this sense, socialization and competition do not indicate the imitation of the unipole’s values and orientations but the elites’ emulation of fellow states’ elites who become successful by enhancing their countries’ resource levels. The emulation of elites by others can lead to a hegemonic system even when there is initially a unique state that adopts for bandwagoning. Thus, an evolutionary game produces results at system-level by assuming states as boundedly-rational non-unitary agents [68].ConstructivismConstructivism provides assumptions for a dynamic framework of repeated interactions and concentrates on continuing processes and practices such as socialization. Socialization is constructivism’s “home turf” and “the process of inducting actors into the norms and rules of a given community” [69, 70]. The theory implies that interactions among lesser states generate endogenous changes in states’ identities, norms, and foreign policies in a unipolar system. States’ interactions can generate different types of anarchies [71]. States can either bandwagon with or balance against the unipole, as it is “appropriate” to do so due to norms and rules on-going interactions generate. Consequently, the central constructivist problem is to find those rules and norms that prevail in unipolar systems through time. Constructivism does not lend a methodological tool to study complex dynamic systems, however.The evolutionary game theory is such a method. The theory implies the ESS as rules and conventions but not as conscious human designs established over time [72]. If bandwagoning is the ESS, it becomes strongly established among states as a self-enforcing rule. The deviant balancers, or, equivalently, mutants, revert to bandwagoning under evolutionary pressures of environment and fitness. All states bandwagoning with the unipole create a new type or “culture” of anarchy, that is, anarchy among states that finally accept the unipole’s superiority [73].Each point on any trajectory leading to an ESS can be interpreted as displaying the dispersal of states’ actions toward the unipole at some period of time. Moreover, any dispersal depends upon the previous one; none can be separated from earlier distribution of actions. Thus, early state practices constitute new ones: it is impossible to treat dispersals independently on an individual basis. In fact, the interpretation parallels structuration theory, as paths toward an ESS demonstrate mutual constitution of evolutionary phases [74]. Each resource comparison is based upon shared knowledge about whether bandwagoners or balancers get fitter in the system. Any ESS emerges as a consequence of on-going comparisons and self-enforcing social conventions.Identities also change during practices. If bandwagoners get fitter, balancers become bandwagoners in the next round. For example, the variants 3 and 4 demonstrate how unipole’s friends transform into balancers and foes into bandwagoners.16 Suppose that both of states initially are all balancers, the environment is
, socialization constitutes a dynamic process of states getting more resourceful. The fitness of bandwagoners improves as balancers always obtain lower resources among them.Structural realism indicates that states are expected to balance against the unipole: balancing is the most successful practice as states are watchful about relative gains. In contrast, the ESS imply that the processes are not unique, as there are infinitely many trajectories leading to overall balancing or bandwagoning depending upon initial conditions. The polymorphic equilibria imply that competition among states for more resources can establish two opposite but successful behaviors. Hence, the most successful alignment policy can be bandwagoning, balancing, or a mixture of them. Competition is not a one-way street.LiberalismPreferences constitute the central liberal variable and stem from various sources ranging from societal ideas and interests to institutions [65]. Liberalism does not either necessitate that states are unitary or rational similar to the foreign policy model assumptions. The game demonstrates that not elites’ preferences but the dispersal of alignment actions in the system drives evolutionary dynamics. States’ adjust their alignment policies toward the unipole through elites’ learning processes under errors and mistakes which can be related to domestic constraints such as the trade-off between domestic and international needs, that is, the “guns or butter” problem.A connection between elites, socialization, and competition processes for hegemonic systems is indeed proposed [66]. States become socialized as their elites accept values and norms the hegemon advances. National leaders progressively accept the hegemon’s norms and values, and, as a consequence, variations in policies towards the hegemon are reduced. It is argued that secondary states’ elites’ internalization of hegemon’s value orientations have nothing to do with forces at system-level ruling structure’s effect upon socialization out and that there are “meager analytic tools to understand the mechanisms and conditions” of socialization [67]. The game proposes mechanisms and conditions for socialization and demonstrates that elites’ learning processes make up forces at system level given the distribution of alignment actions. Any ESS of the game derives from elites’ learning processes and describes policy dispersal across states. An alignment policy becomes evolutionarily stable as system environments set up unipolar constraints affecting elites’ learning (including organizations’ operations). Thus, structure’s effect upon socialization can matter. It is possible that elites’ learning and organizations’ operations imply mistakes, for example, a state may adopt balancing while bandwagoning produce higher resource amounts, or, making no mistakes and achieving a boost in their state’s domestic resources. In this sense, socialization and competition do not indicate the imitation of the unipole’s values and orientations but the elites’ emulation of fellow states’ elites who become successful by enhancing their countries’ resource levels. The emulation of elites by others can lead to a hegemonic system even when there is initially a unique state that adopts for bandwagoning. Thus, an evolutionary game produces results at system-level by assuming states as boundedly-rational non-unitary agents [68].ConstructivismConstructivism provides assumptions for a dynamic framework of repeated interactions and concentrates on continuing processes and practices such as socialization. Socialization is constructivism’s “home turf” and “the process of inducting actors into the norms and rules of a given community” [69, 70]. The theory implies that interactions among lesser states generate endogenous changes in states’ identities, norms, and foreign policies in a unipolar system. States’ interactions can generate different types of anarchies [71]. States can either bandwagon with or balance against the unipole, as it is “appropriate” to do so due to norms and rules on-going interactions generate. Consequently, the central constructivist problem is to find those rules and norms that prevail in unipolar systems through time. Constructivism does not lend a methodological tool to study complex dynamic systems, however.The evolutionary game theory is such a method. The theory implies the ESS as rules and conventions but not as conscious human designs established over time [72]. If bandwagoning is the ESS, it becomes strongly established among states as a self-enforcing rule. The deviant balancers, or, equivalently, mutants, revert to bandwagoning under evolutionary pressures of environment and fitness. All states bandwagoning with the unipole create a new type or “culture” of anarchy, that is, anarchy among states that finally accept the unipole’s superiority [73].Each point on any trajectory leading to an ESS can be interpreted as displaying the dispersal of states’ actions toward the unipole at some period of time. Moreover, any dispersal depends upon the previous one; none can be separated from earlier distribution of actions. Thus, early state practices constitute new ones: it is impossible to treat dispersals independently on an individual basis. In fact, the interpretation parallels structuration theory, as paths toward an ESS demonstrate mutual constitution of evolutionary phases [74]. Each resource comparison is based upon shared knowledge about whether bandwagoners or balancers get fitter in the system. Any ESS emerges as a consequence of on-going comparisons and self-enforcing social conventions.Identities also change during practices. If bandwagoners get fitter, balancers become bandwagoners in the next round. For example, the variants 3 and 4 demonstrate how unipole’s friends transform into balancers and foes into bandwagoners.16 Suppose that both of states initially are all balancers, the environment is 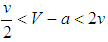 , and that the type-1 states are the traditional friends of the unipole and the type-2 states are the unipole’s traditional foes. Once states recognize that some of them are the friends and some others are the foes of the unipole, their actions become dependent on these traits playing different roles, for example: “if we are the friends of the unipole, then we adopt bandwagoning, if we are the foes of the unipole, we adopt balancing, or vice versa.” The role is the expected behavior of states possessing a given identity. Thus, identities are positions and roles refer to behavior [75]. As a result, socialization and competition become role specific and consequences of enactment of roles, as states differentiate themselves and assign each among them to a different role. States are distinguished as balancer-friends and bandwagoner-foes or vice versa while their actions towards the unipole evolve.17Furthermore, the knowledge about the asymmetry helps to explain the selection of the ESS depending upon the initial dispersal of states as friends and foes. If “friends” are expected to align with the unipole, the evolutionary dynamics can demonstrate that “foes” rather than friends align with the unipole to such an extent that all friends turn into balancers if foe-bandwagoners are more numerous than friend-bandwagoners. The foreign policy model implies that individual states’ decision makers’ role-conceptions and unipolar environments determine the ultimate dispersal of actions toward the unipole.Assortative matching goes even one step further by assuming that the friends of the unipole do not compare their resource performances with those of the enemies of the unipole at the outset, therefore conditional actions and roles do not matter. And even if some differentiate each other as unipole’s allies or enemies but some do not, the resulting ESS would not differ from those implied by random matching in non-homogeneous populations. Hence, socialization processes can lead to hegemony or global balance when states’ actions are all pre-determined so that their identities are all the same or role-playing applies to some group within the population.
, and that the type-1 states are the traditional friends of the unipole and the type-2 states are the unipole’s traditional foes. Once states recognize that some of them are the friends and some others are the foes of the unipole, their actions become dependent on these traits playing different roles, for example: “if we are the friends of the unipole, then we adopt bandwagoning, if we are the foes of the unipole, we adopt balancing, or vice versa.” The role is the expected behavior of states possessing a given identity. Thus, identities are positions and roles refer to behavior [75]. As a result, socialization and competition become role specific and consequences of enactment of roles, as states differentiate themselves and assign each among them to a different role. States are distinguished as balancer-friends and bandwagoner-foes or vice versa while their actions towards the unipole evolve.17Furthermore, the knowledge about the asymmetry helps to explain the selection of the ESS depending upon the initial dispersal of states as friends and foes. If “friends” are expected to align with the unipole, the evolutionary dynamics can demonstrate that “foes” rather than friends align with the unipole to such an extent that all friends turn into balancers if foe-bandwagoners are more numerous than friend-bandwagoners. The foreign policy model implies that individual states’ decision makers’ role-conceptions and unipolar environments determine the ultimate dispersal of actions toward the unipole.Assortative matching goes even one step further by assuming that the friends of the unipole do not compare their resource performances with those of the enemies of the unipole at the outset, therefore conditional actions and roles do not matter. And even if some differentiate each other as unipole’s allies or enemies but some do not, the resulting ESS would not differ from those implied by random matching in non-homogeneous populations. Hence, socialization processes can lead to hegemony or global balance when states’ actions are all pre-determined so that their identities are all the same or role-playing applies to some group within the population.6. Conclusions
- We aimed rather to generate useful insights than to conduct a rigorous test. Using a simple evolutionary framework, we investigated the evolutionary directions that states’ actions toward a unipole can take. Few parameters used produced different paths of competition and socialization in unipolar systems. It is found that the direction of these evolutionary processes depends upon the environment of unipolar systems, resources available to bandwagoners and balancers, cost of complying with the unipole, and, in some cases, initial composition of the population in terms of bandwagoners and balancers.There are possible extensions of the model. One is the inclusion of taking no action as a third strategy. Other plausible extensions include the use of different dynamics and game parameters. It is possible to assume that resources shared among balancers and among bandwagoners sum up to a constant value such as V + v = l with V, v > 0 amounting to a relationship between V and v. If l = 1, for example, one unit increment in one implies one unit reduction in the other. The discussion is limited to general security terms. The implications help to organize insights and simple ideas about how states react to the unipole. The values of model’s three parameters would differ across different global issues. To bandwagon with the unipole in protection of international environment, finance, proliferation of nuclear weapons technology, or counterterrorism would not produce the same amount of benefit and loss of autonomy cost. Structural constraints would vary across the multiplicity of issues the global agenda contains; therefore evolutionary paths would vary accordingly. The superposition of these processes hints at complex evolutions of strategies states may adopt towards the unipole.
Notes
- 1. Bennett (1995) indicates that game models are mostly criticized for their static nature and their requirement of rationality assumption: Bennett, Peter G. (1995). “Modelling Decisions in International Relations: Game Theory and Beyond,” Mershon International Studies Review 39 (1): 19-52.2. We use bandwagoners as the synonym of states that bandwagon with the unipole from now on.3. It is impossible to review all theories explaining balancing and bandwagoning in few pages. See, for example, Jervis (1978) and Schweller (1994) for the role of offense-defense balance and states’ motives in states’ alignment decisions.4. Thayer (2000) connects evolutionary theory with classical realism to justify states’ dominance motive as resulting from human evolution and selfish gene: Thayer, Bradley A. (2000) “Bringing in Darwin: Evolutionary Theory, Realism, and International Politics.” International Security 25 (2): 124-151. Masters (1983) searches for general links between biology and political theory: Masters, Roger D. (1983). “The Biological Nature of the State.” World Politics 35 (2): 161-193.5. Legro and Moravcsik (1999: 14) state that Waltz’s assumption becomes is vague and elastic: Legro, Jeffrey W. and Andrew Moravcsik (1999). “Is Anybody Still a Realist?” International Security 24 (2): 5-55.6. Levy (2003: 134-135) argues that balancing behavior “comes in degrees” similar to “nonbalancing” behavior covering bandwagoning, buck-passing, chainganging. 7. Nowadays, the United States does not face global balancing efforts as states perceive it as “benign”: Kupchan (1998). Lieber and Alexander (2005: 113) similarly argue that states do not balance against the United States because it is selectively aggressive and not broadly threatening after 9/11 attacks.8. Axelrod (1984) finds that TIT-FOR-TAT is the most successful strategy in tournaments of infinitely repeated Prisoner’s Dilemma. The ESS of the game does not confirm this finding (Osborne, 2004: 440-441; Samuelson, 1998: 20).9. Remark that x increases when V increases and decreases when either a or v increases.10. Differential equations and formal deductions are placed in the appendix. The equations set up fitness conditions as replicator dynamics.11. It is impossible to discuss each aspect of these theories in terms of evolutionary processes. Therefore, we limit our discussion with theoretical implications for competition and socialization processes.12. Deudney and Ikenberry (1999) provide an empirical approximation to this case by indicating that even if states get institutionalized U.S. assurances, they could defect frıom the United States. They qualify such systems as “punctuated hegemony:” Deudney, Daniel and John Ikenberry (1999) “Realism, Structural Liberalism and the Western Order,” in Ethan A. Kapstein and Michael Mastanduno (eds), Unipolar Politics: Realism and State Strategies After the Cold War New York: Columbia University Press, 103-137. 13. Elman (2006) in turn argues that structural realism is not an evolutionary approach to international politics but can be used to analyze foreign policy of individual states.14. For an opposite view, see Morrow (1988: 89). Levy (1994: 298) argues that socialization and selection require rational learning.15. Resende-Santos (1995) notes that Waltz’s definition of socialization is more convenient for social systems than for a theory of international politics considered as asocial: Resende-Santos, J. (1995). “Anarchy and the Emulation of Military Systems,” Security Studies, 5 (3): 190-245. 16. Pape (2005, 2006) argues that France, Germany, and even Japan are nowadays involved in soft-balancing measures targeting the United States. Soft balancing covers the use of international institutions, economic measures, and diplomacy to delay, frustrate, and undermine unilateral U.S. policies without directly challenging the United States. These moves can be interpreted as balancing acts.17. Thies (2003: 546) notes that role playing constitutes a bridge between constructivism and structural realism proving an ideational meaning for socialization processes.
Appendix
- Variant 1The evolution of bandwagoning and balancing is given by:
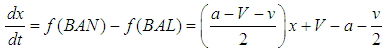 | (9) |
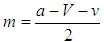 and
and 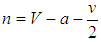 , we can write:
, we can write: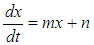 | (10) |
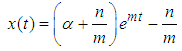 | (11) |
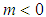 by assumption,
by assumption, 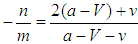 , and α denotes any initial condition.Let
, and α denotes any initial condition.Let 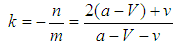 . There are three stable equilibria:Case 1 If k ≥ 1, that is,
. There are three stable equilibria:Case 1 If k ≥ 1, that is, 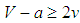 , x(t) converges to 1.Case 2 If k ≤ 0, that is,
, x(t) converges to 1.Case 2 If k ≤ 0, that is, 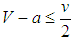 , x(t) converges to 0.Case 3 If
, x(t) converges to 0.Case 3 If 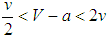 , x(t) converges to k.Variant 2The following system of differential equations describe linear dynamicsassumption:
, x(t) converges to k.Variant 2The following system of differential equations describe linear dynamicsassumption: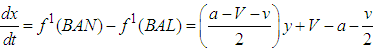 | (12) |
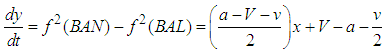 | (13) |
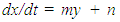 | (14) |
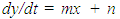 | (15) |
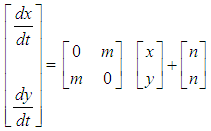 | (16) |
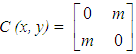 . Setting | C − λI | = 0, we obtain the characteristic roots λ1 = m, λ2 = − m. The general solution is therefore:
. Setting | C − λI | = 0, we obtain the characteristic roots λ1 = m, λ2 = − m. The general solution is therefore: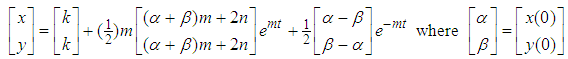 | (17) |
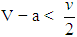 , it is unstable if
, it is unstable if 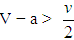 .Case 2 (0, 1) is stable if
.Case 2 (0, 1) is stable if 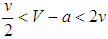 , it is unstable if V − a > 2v, or V − a < 2v.Case 3 (1, 0) is stable if
, it is unstable if V − a > 2v, or V − a < 2v.Case 3 (1, 0) is stable if 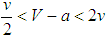 , it is unstable if V − a > 2v, or V − a < 2v.Case 4 (1, 1) is stable if V − a > 2v, it is unstable if V − a < 2v.Variant 3The evolution of bandwagoning and balancing is given by:
, it is unstable if V − a > 2v, or V − a < 2v.Case 4 (1, 1) is stable if V − a > 2v, it is unstable if V − a < 2v.Variant 3The evolution of bandwagoning and balancing is given by: 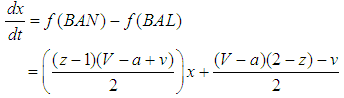 | (18) |
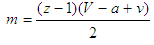 and
and 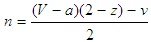 , we can write:
, we can write: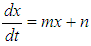 | (19) |
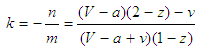 implying additional conditions on the probability z:Case 1 If k ≥ 1, that is,
implying additional conditions on the probability z:Case 1 If k ≥ 1, that is, 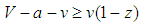 , x(t) converges to 1.Case 2 If k ≤ 0, that is,
, x(t) converges to 1.Case 2 If k ≤ 0, that is, 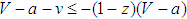 , x(t) converges to 0.Case 3 If
, x(t) converges to 0.Case 3 If 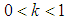 , that is,
, that is, 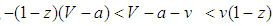 , x(t) converges to k.
, x(t) converges to k. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML