-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2017; 6(1): 15-20
doi:10.5923/j.jgt.20170601.03

Capital Structure and Signalling - An Impossibility Result
Volker Bieta
Department of Economics, Dresden Technical University, Helmholtzstraße, Dresden, Germany
Correspondence to: Volker Bieta, Department of Economics, Dresden Technical University, Helmholtzstraße, Dresden, Germany.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A simple project funding (borrower-lender) game with limited liability and asymmetric information is considered. The paper deals with the question whether a debt-to-equity ratio is a signal to reveal projects’ risks to the lender. The ratio is chosen by the borrower before receiving a loan for funding a project. The lender has ex-ante hidden information about the risks caused by the borrower’s project choice. Probability distributions with continuous densities for the projects’ cash flows are assumed. According to their risks, the projects are ranked by second-order stochastic dominance. We find a game defined by these assumptions may exclude a positive signalling result. That the assumption of a continuous density instead of a discrete density on two points is decisive for the equilibrium’s type is the main result.
Keywords: Second-order stochastic dominance, Game theory, Perfect Bayesian equilibrium
Cite this paper: Volker Bieta, Capital Structure and Signalling - An Impossibility Result, Journal of Game Theory, Vol. 6 No. 1, 2017, pp. 15-20. doi: 10.5923/j.jgt.20170601.03.
Article Outline
1. Introduction
- In the literature has been widely discussed how different information settings influence the decisions of banks and investors in the credit market. Mostly, we have a situation where the players do not have complete information about the details of interaction. Usually, this takes place when the lender is uncertain of the borrower’s risk type. Because of different probability distributions of the unknown parameter games of asymmetric information are played.In project funding a game of asymmetric information is to be considered when only the borrower knows the real risk of the project he chooses but the lender does not. Typically, the assumption of a discrete probability distribution on two points for the cash flows generated by risky projects leads to the well-known positive signalling results. If so, from the lender’s side appropriately defined financial measures are helpful signals for revealing projects’ risks with a high degree of certainty.However, less well-known is how signalling works when the cash flows of uncertain projects are not modelled by a two point probability distribution. Using the debt-to-equity ratio, chosen by the borrower before receiving a lender’s loan to finance a project, as measure we deal with the question whether a positive signalling result can still be confirmed when probability distributions with continuous densities for the cash flows are assumed. More precisely, in a borrower-lender game without cash flows’ restrictions due to discrete distributions on two points it is questioned whether a separating perfect Bayesian equilibrium (PBE) exists. Before proving a non-positive result, at first, a short justification for our analysis is given. For that purpose the assumptions of three pioneered works are sketched briefly (i) Ross [1] presumes high debt levels as signals for high quality investments. The firm’s probability distributions of projects’ returns are different by first-order stochastic dominance. In the paper, the projects are ranked according to second-order stochastic dominance (ssd) (see [2]) characterized by mean-preserving spreads (mps), (ii) Bester [3] assumes the loan level as signal for the probability of default. The lender is imperfectly informed about the investor’s risk type. By using a discrete probability distribution on two points, the project’s outcome is either a zero cash flow if the project fails or a positive cash flow if the project succeeds. In the paper, a continuum of outcomes is assumed. The size of the projects is exogenously given by an initial outlay. By choosing the loan level, the investor also decides on the level of equity, he is willing to commit to the project, and (iii) as well, loan size as signal of projects’ risks is supposed by Milde/Riley [4]. The probability distributions of projects’ returns are different by ssd. Just as Bester, Milde/Riley assume that the return depend on both a quality parameter known only the loan applicant and the loan size. There is no upper bound for the loan size choice. Assuming limited liability, the paper deals with the question whether the debt-to-equity ratio is a signal for revealing projects’ risks.The remainder proceeds as follows. Section 2 is divided in two subsections. Firstly, we define a simple borrower-lender game (see 2.1). Secondly, for solving the game the PBE is used (see 2.2). Section 3 concludes. The main result (the non-existence of a separating PBE) is proven indirectly. The proofs are collected in an Appendix.
2. The Setting
- A firm loans a credit to fund a one period project with uncertain cash flows. There are two types of risky projects. Increasing risk is expressed by mps of the projects’ cash flows. The type is private knowledge of the firm. The bank only knows that
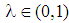 have low risk (class 1) and
have low risk (class 1) and 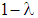 have high risk (class 2). It is unknown which project is funded after receiving a loan. The stochastic of the types is common knowledge. The risk-free interest rate
have high risk (class 2). It is unknown which project is funded after receiving a loan. The stochastic of the types is common knowledge. The risk-free interest rate  is zero.Independent of the type of risk running a project requires financial funds
is zero.Independent of the type of risk running a project requires financial funds  . The loan volume 1 (the debt-to-equity ratio) is to be chosen by the firm. A loan of at least
. The loan volume 1 (the debt-to-equity ratio) is to be chosen by the firm. A loan of at least 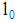 and
and 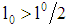 is assumed (Note that only a ratio bigger than 1 implies project funding is risky for the bank). Depending on the loan amount chosen by the firm for any possible loan
is assumed (Note that only a ratio bigger than 1 implies project funding is risky for the bank). Depending on the loan amount chosen by the firm for any possible loan 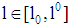 the bank decides on the extra charge to the risk less interest rate by choosing schemes of loan offerings (claims)
the bank decides on the extra charge to the risk less interest rate by choosing schemes of loan offerings (claims) 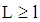 . The difference
. The difference 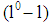 is covered by the equity of the owners of the firm. The players are risk-neutral. Now, we question whether a debt-to-equity ratio is a signal for reducing the bank’s uncertainty of the firm’s risk type. The idea of the firm’s risk self-selection is the following: the bank unable to identify the risk of a project chosen by the firm offers for revealing the firm’s hidden risk some different loan contracts to conclude from the ratio chosen by the firm with certainty what the firm’s risk type will be.
is covered by the equity of the owners of the firm. The players are risk-neutral. Now, we question whether a debt-to-equity ratio is a signal for reducing the bank’s uncertainty of the firm’s risk type. The idea of the firm’s risk self-selection is the following: the bank unable to identify the risk of a project chosen by the firm offers for revealing the firm’s hidden risk some different loan contracts to conclude from the ratio chosen by the firm with certainty what the firm’s risk type will be. 2.1. The Borrower-Lender Game
- Before starting the analysis, foresighted we summarize briefly. By assuming (i) a continuous projects’ cash flow probability distribution, (ii) a projects’ ranking by ssd, and (iii) limited borrowers’ liability a game is analyzed in which, how we show, assumption (i) is decisive for the type of the PBE. The sequence of players’ moves is depicted in figure 1.
 | Figure 1. Players’ sequence of moves |
 or type
or type 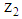 . Both projects require the same initial amount
. Both projects require the same initial amount 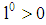 . (ii) The projects’ cash flows are uncertain. The random variable
. (ii) The projects’ cash flows are uncertain. The random variable  is given by the distribution
is given by the distribution 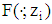 and the density
and the density 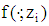 with
with 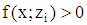 for all
for all 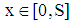 and
and 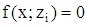 else. (iii) Both distributions have the same expected value
else. (iii) Both distributions have the same expected value 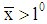 . The
. The 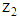 -project is riskier than the
-project is riskier than the 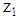 -project, which is expressed by ssd. The stochastic of the projects’ types is common knowledge. (iv) Player B does not know player E’s type. Player E chooses the debt-to-equity ratio (the loan face value)
-project, which is expressed by ssd. The stochastic of the projects’ types is common knowledge. (iv) Player B does not know player E’s type. Player E chooses the debt-to-equity ratio (the loan face value) 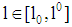 . Player B chooses (supplies) a loan scheme (the claim)
. Player B chooses (supplies) a loan scheme (the claim) 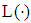 for any
for any 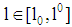 .The cash flows are calculated as follows: if a loan with a face value 1 and a corresponding claim
.The cash flows are calculated as follows: if a loan with a face value 1 and a corresponding claim 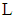 are accepted by player E, then player E’s cash flow is given by
are accepted by player E, then player E’s cash flow is given by  if
if 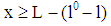 is valid (case of non-insolvency). Otherwise, player E’s cash flow is given by
is valid (case of non-insolvency). Otherwise, player E’s cash flow is given by 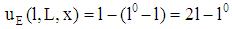 (case of insolvency). At
(case of insolvency). At  player B’s cash flow is given by
player B’s cash flow is given by 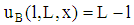 if
if 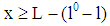 is valid and
is valid and  else.Remark 1: (i) The analysis is limited to project funding with limited liability. In case of insolvency, the bank’s rights are restricted to the cash flows generated by the firm’s (the owners of the firm) equity. (ii) For keeping the analysis simple a risk less interest rate
else.Remark 1: (i) The analysis is limited to project funding with limited liability. In case of insolvency, the bank’s rights are restricted to the cash flows generated by the firm’s (the owners of the firm) equity. (ii) For keeping the analysis simple a risk less interest rate 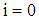 is assumed, whereat
is assumed, whereat 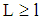 is valid. (iii) Running a project requires a strictly positive minimum debt-to-equity ratio. More than the half of the total investment sum of the project to be a loan is required. Otherwise, independent of the real risk type a project is certain for the bank. Due to
is valid. (iii) Running a project requires a strictly positive minimum debt-to-equity ratio. More than the half of the total investment sum of the project to be a loan is required. Otherwise, independent of the real risk type a project is certain for the bank. Due to 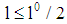 the liable equity must be at least as large as the bank’s claim for loans.
the liable equity must be at least as large as the bank’s claim for loans. 2.2. The Game Theoretic Analysis
- To analyze the borrower-lender game the PBE is used. It is described by a pair
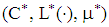 with
with 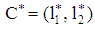 . Here,
. Here, 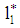 and
and 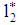 denote the loan size chosen by the firm depending on its type. The bank’s system of beliefs (i.e., a probability assessment) with respect to the firm’s risk types
denote the loan size chosen by the firm depending on its type. The bank’s system of beliefs (i.e., a probability assessment) with respect to the firm’s risk types  is denoted by
is denoted by 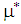 . For a chosen ratio given by the requested loan par value 1 the bank’s system of beliefs is given by
. For a chosen ratio given by the requested loan par value 1 the bank’s system of beliefs is given by 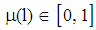 (i.e., the bank’s subjective probability that the chosen project is of type
(i.e., the bank’s subjective probability that the chosen project is of type 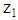 ) and
) and 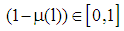 (i.e., the bank‘s subjective probability that the chosen project is of type
(i.e., the bank‘s subjective probability that the chosen project is of type 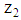 ).For solving the game, at first, we determine the type specific expected payoffs of the players if the firm accepts the bank’s claim
).For solving the game, at first, we determine the type specific expected payoffs of the players if the firm accepts the bank’s claim 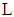 with a par value f. Denotes
with a par value f. Denotes 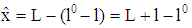 the boundary of insolvency we get (1)
the boundary of insolvency we get (1) 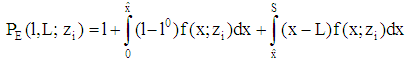 and (2)
and (2) 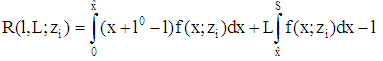 . Due to the beliefs
. Due to the beliefs 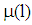 the bank’s type specific expected payoff is given by (3)
the bank’s type specific expected payoff is given by (3) 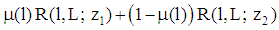 . Denotes
. Denotes 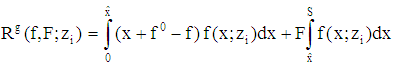 the bank’s type-specific (conditional) expected payoff, then the bank’s claim supply
the bank’s type-specific (conditional) expected payoff, then the bank’s claim supply 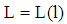 for a par value 1 is implicitly given by (4)
for a par value 1 is implicitly given by (4) 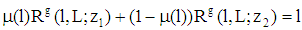 .Remark 2 We assume perfect competition for the firms within a homogeneous group of banks. A loan contract
.Remark 2 We assume perfect competition for the firms within a homogeneous group of banks. A loan contract 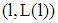 satisfying (4) includes the minimum claim
satisfying (4) includes the minimum claim 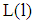 of a risk neutral bank with respect to a loan with par value 1 in a perceived situation
of a risk neutral bank with respect to a loan with par value 1 in a perceived situation 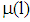 . More precisely, in the game the bank always offers the best possible contract to the firm since the lowest possible charge on the risk free interest rate is chosen by the bank. Next, we prove the main result. The basic idea is illustrated in figure 2 below. Referring to the Appendix first of all a few remarks about some properties of the firm’s indifference curves (see remark 3 and remark 4) will be made briefly: (i) The slope of a type i-firm curve at
. More precisely, in the game the bank always offers the best possible contract to the firm since the lowest possible charge on the risk free interest rate is chosen by the bank. Next, we prove the main result. The basic idea is illustrated in figure 2 below. Referring to the Appendix first of all a few remarks about some properties of the firm’s indifference curves (see remark 3 and remark 4) will be made briefly: (i) The slope of a type i-firm curve at  is given by (5)
is given by (5) 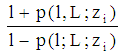 . (Note: Due to (6)
. (Note: Due to (6) 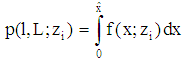 is the probability of insolvency of the loan contract
is the probability of insolvency of the loan contract 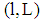 for the project
for the project 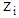 ), (ii) The curves of the types are strictly monotonic increasing and strictly convex on
), (ii) The curves of the types are strictly monotonic increasing and strictly convex on 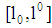 . The mapping
. The mapping 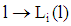 for all
for all 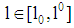 (the type i-line) is identical to the curve of a type i-firm at the level
(the type i-line) is identical to the curve of a type i-firm at the level 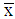 . (Note:
. (Note: 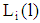 is defined by
is defined by 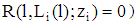 ), and (iii) Since
), and (iii) Since 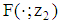 is a mps of
is a mps of 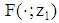 the inequality
the inequality 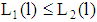 is valid for all
is valid for all 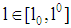 .
.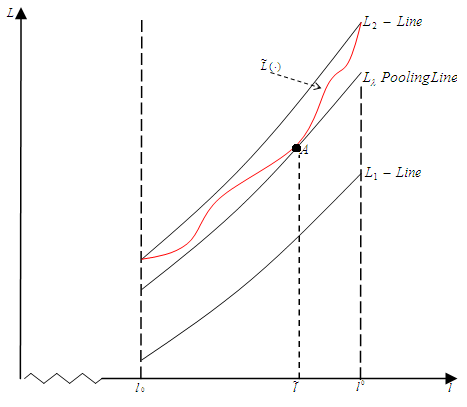 | Figure 2. No type-separation |
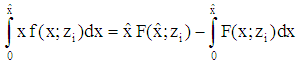 the validity of
the validity of 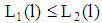 in (iii) is proven indirectly. Two cases are to be considered. Case (a) If
in (iii) is proven indirectly. Two cases are to be considered. Case (a) If 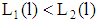 for all
for all 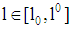 , then each PBE is of a pooling type. Suppose there exists a separating PBE
, then each PBE is of a pooling type. Suppose there exists a separating PBE 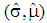 with
with 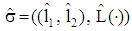 ,
, 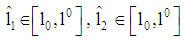 , and
, and 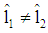 . Due to (4), then we get
. Due to (4), then we get 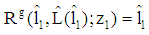 and
and 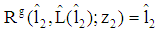 . (Note:
. (Note: 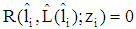 holds according to
holds according to 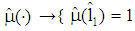 ,
, 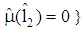 ). Thus,
). Thus, 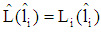 holds as well. Therefore, there is an incentive to deviate for a type 2-firm. (Note: If a type 2-firm asks for a loan with par value
holds as well. Therefore, there is an incentive to deviate for a type 2-firm. (Note: If a type 2-firm asks for a loan with par value 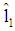 instead of
instead of 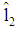 , then a higher indifference curve is reached according to
, then a higher indifference curve is reached according to 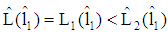 ).We get a PBE of a pooling type
).We get a PBE of a pooling type 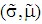 with
with 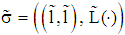 and
and 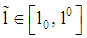 if
if 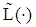 can be chosen such that the mapping on
can be chosen such that the mapping on 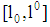 belonging to it is located beyond
belonging to it is located beyond 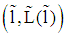 (see A in figure 2). Here,
(see A in figure 2). Here, 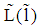 is given by
is given by 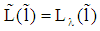 and
and 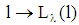 defines the so called “pooling line” for all
defines the so called “pooling line” for all 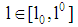 . (Note:
. (Note: 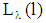 is given by
is given by 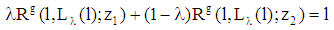 for all
for all  ). Due to (4),
). Due to (4),  satisfy
satisfy  . (Note: A choice
. (Note: A choice  is possible if the indifference curve of a type 1-firm at
is possible if the indifference curve of a type 1-firm at 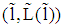 (see A in figure 2) does not intersect
(see A in figure 2) does not intersect 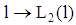 for all
for all 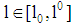 (type 2-line) since
(type 2-line) since 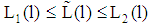 must be satisfied for all
must be satisfied for all 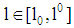 due to (4)).This case occurs if the project with lower risk has lower probability of insolvency for all contracts
due to (4)).This case occurs if the project with lower risk has lower probability of insolvency for all contracts 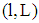 with
with 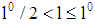 and
and 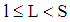
 must hold (see (6)). If
must hold (see (6)). If 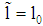 , then
, then 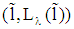 is an equilibrium of a pooling type for all loans
is an equilibrium of a pooling type for all loans 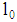 since the indifference curve of a type 1-firm does not intersect the indifference curve of a type-2 firm at
since the indifference curve of a type 1-firm does not intersect the indifference curve of a type-2 firm at 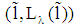 . (Note:
. (Note: 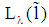 is defined by
is defined by 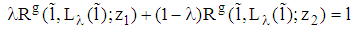 (the pooling condition) and
(the pooling condition) and 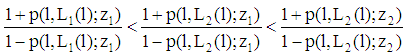 for all
for all 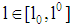 holds since the slope of
holds since the slope of 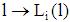 for all
for all 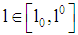 (type i-line) is given by
(type i-line) is given by 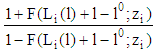 . Hence, the slope of the indifference curve of a type 1-firm is always smaller than the slope of the indifference curve of a type 2-firm). Remark 3 (i) In case (a) we discussed
. Hence, the slope of the indifference curve of a type 1-firm is always smaller than the slope of the indifference curve of a type 2-firm). Remark 3 (i) In case (a) we discussed 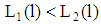 for all
for all 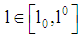 . If PBE exist, then they are of a pooling type. In equilibrium, the ratio chosen by the firm does not have the separation property. (Note: There are no schemes putting incentives for both types of the firm by which the self-selection property of the ratio leads to the disclosure of the firm’s types. However, it is obvious that signalling of the real type is in a type 1-firm’s interest (see figure 2)). (ii) PBE exist if for all loan contracts
. If PBE exist, then they are of a pooling type. In equilibrium, the ratio chosen by the firm does not have the separation property. (Note: There are no schemes putting incentives for both types of the firm by which the self-selection property of the ratio leads to the disclosure of the firm’s types. However, it is obvious that signalling of the real type is in a type 1-firm’s interest (see figure 2)). (ii) PBE exist if for all loan contracts 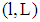 with
with 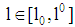 and
and 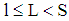 the less risky project has the lower probability of insolvency. Finally, the extreme case (b) of a volume
the less risky project has the lower probability of insolvency. Finally, the extreme case (b) of a volume 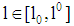 with
with 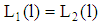 is to be analyzed. Here, a separating equilibrium exists as well. Suppose there is any
is to be analyzed. Here, a separating equilibrium exists as well. Suppose there is any 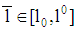 with
with 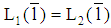 . It is straightforward to see, if
. It is straightforward to see, if 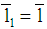 ,
, 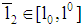 ,
, 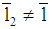 , and
, and 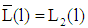 for all
for all 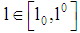 and if
and if 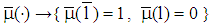 for all
for all 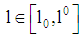 and
and  , then
, then 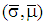 with
with 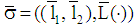 is a PBE. According to (4), the system of beliefs
is a PBE. According to (4), the system of beliefs 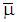 and the strategy
and the strategy  are consistent.Remark 4 (i) Each loan amount
are consistent.Remark 4 (i) Each loan amount 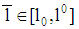 with
with 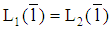 generates a pooling PBE. (Note: By choosing
generates a pooling PBE. (Note: By choosing 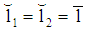 and
and 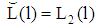 we get a pooling PBE
we get a pooling PBE 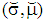 with
with 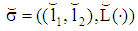 and
and 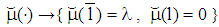 for all
for all 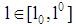 with
with 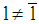 ). (ii) In case (b) a loan amount
). (ii) In case (b) a loan amount 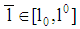 with
with 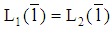 is part of each pooling PBE. (Note: If a pooling PBE
is part of each pooling PBE. (Note: If a pooling PBE 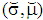 with
with 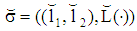 ,
, 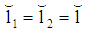 ,
, 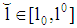 ,
, 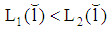 , and
, and 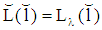 exists, then there is an incentive for a type 1-firm to deviate towards
exists, then there is an incentive for a type 1-firm to deviate towards 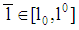 with
with 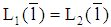 (i.e., reaching a curve at level
(i.e., reaching a curve at level 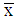 instead of a lower level is preferred by a type 1-firm). Note furthermore,
instead of a lower level is preferred by a type 1-firm). Note furthermore, 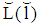 is defined by
is defined by 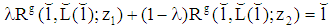 and
and  as well as
as well as 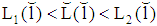 must be satisfied necessarily). (iii) In all separating PBE a type i-firm gets the same expected payoff
must be satisfied necessarily). (iii) In all separating PBE a type i-firm gets the same expected payoff 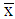 . This remains true for all pooling PBE. Thus, in case (b) all PBE are equivalent with respect to their payoffs. (iv)
. This remains true for all pooling PBE. Thus, in case (b) all PBE are equivalent with respect to their payoffs. (iv) 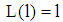 is valid for all loan amounts
is valid for all loan amounts 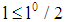 and claim schemes
and claim schemes 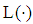 satisfying (4). The bank has no risk since the liable equity is sufficiently large. We have
satisfying (4). The bank has no risk since the liable equity is sufficiently large. We have 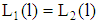 .
.3. Concluding Remark
- In a simple project funding game with limited liability and asymmetric information we deal with the question whether banks can conclude from the debt-to-equity ratio chosen by firms what projects’ risks will be. We cannot confirm a positive signalling result in general: all PBE are pooling equilibria if projects with continuously distributed cash flows are ranked according to second-order stochastic dominance and if the riskier project has a higher probability of insolvency for all chosen ratios larger than 1. This remains true if the less risky project has the higher probability of insolvency.
Appendix
- Proposition 1 The slope of firm i’s indifference curve at
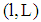 is given by
is given by 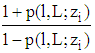 Proof Let
Proof Let 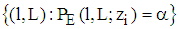 be the indifference curve of a type i-firm implicitly defined by
be the indifference curve of a type i-firm implicitly defined by 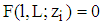 if
if 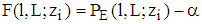 and let
and let 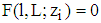 be denoted by
be denoted by 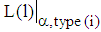 . Then, the slope at
. Then, the slope at 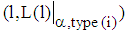 is given by
is given by 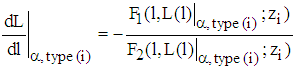 such that
such that 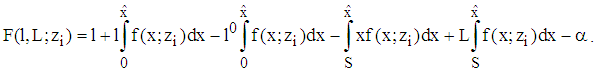 Hence, according to
Hence, according to 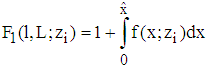 and
and 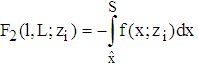 we have
we have 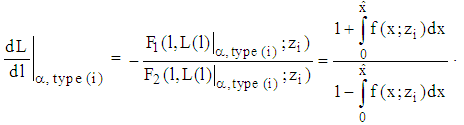 Corollary The indifference curves of a type i-firm are strictly monotonic increasingProposition 2 The indifference curves of a type i-firm are strictly convex on
Corollary The indifference curves of a type i-firm are strictly monotonic increasingProposition 2 The indifference curves of a type i-firm are strictly convex on 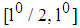 Proof Holds due to
Proof Holds due to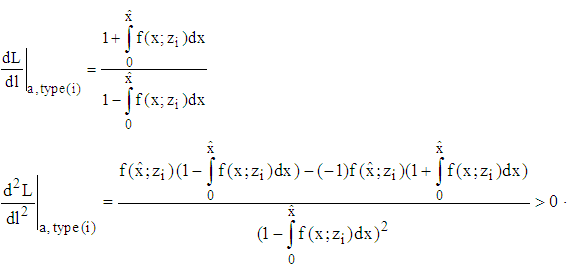 Proposition 3 If
Proposition 3 If 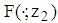 is a mps of
is a mps of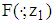 , then
, then 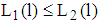 holds for all
holds for all  Proof Suppose Proposition 3 does not hold, then
Proof Suppose Proposition 3 does not hold, then 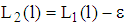 must hold for any
must hold for any  . Using
. Using 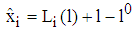 and
and 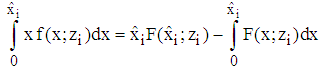 we get
we get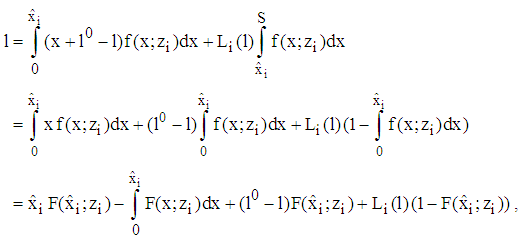 such that with
such that with 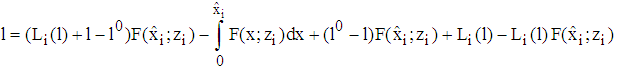
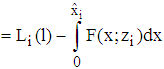 , by conclusion,
, by conclusion, 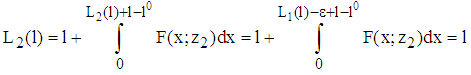
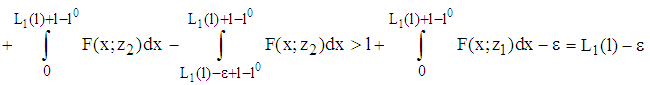 holds as well. Here, the inequality is valid according to ssd. Hence,
holds as well. Here, the inequality is valid according to ssd. Hence, 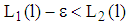 . This contradicts the assumption. Finally, it remains to be shown
. This contradicts the assumption. Finally, it remains to be shown 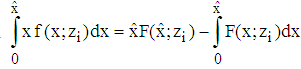 . The anti-derivative of
. The anti-derivative of 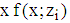 is given by
is given by 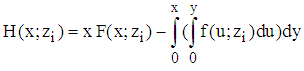 according to
according to 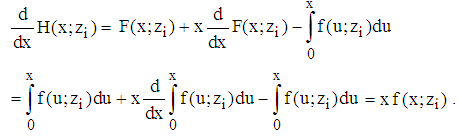 Hence,
Hence, 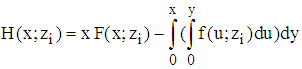 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML