-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2017; 6(1): 1-6
doi:10.5923/j.jgt.20170601.01

Extensions of Bertrand's Differentiated Products Model
Yigal Gerchak
Department of Industrial Engineering, Tel-Aviv University, Israel
Correspondence to: Yigal Gerchak, Department of Industrial Engineering, Tel-Aviv University, Israel.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We consider two extensions of Bertrand's celebrated duopoly and tri-opoly models of differentiated products. One extension consists of generalizing linear production costs to convex ones. For quadratic costs, we obtain the symmetric equilibrium explicitly. The other is a two-period model where the demand in the second period depends on the price in the first period (reference price) as well. We obtain an explicit solution to the second period problem and characterize the optimal first period price.
Keywords: Bertrand, Non-Linear Costs, Reference Prices
Cite this paper: Yigal Gerchak, Extensions of Bertrand's Differentiated Products Model, Journal of Game Theory, Vol. 6 No. 1, 2017, pp. 1-6. doi: 10.5923/j.jgt.20170601.01.
Article Outline
1. Introduction
- Bertrand's model is one of the classical models of differentiated duopoly and is a forerunner of the Nash equilibrium. In this model demand for each firm increases in the competitor's price while decreasing in its own price [1-3]. In this classical model production costs are usually assumed to be linear. As such is often not the case, (e.g. [4, 5]), we explore duopoly and tri-opoly [6] scenarios with increasing marginal production costs. We also consider a two-period model where a firm's demand in the second period depends on its and its competitors’ price in the first period ("reference price"), as well on the second period prices [7, 8]. While such consumer behavior may not be entirely rational, there is ample empirical evidence in the marketing and psychology literature for its prevalence.For completeness, we first sketch the well-known Bertrand's linear duopoly model of differentiated products [2, 9] and then do so for a tri-opoly (cf. [6, 10]) and we include comparative statics. We show conditions under which a tri-opolist would charge a higher price than a duopolist. We then generalize them to non-linear production costs, where we focus on the case of quadratic costs for which we obtain an explicit solution. Finally, we consider a two-period duopoly with reference prices.
2. The Basic Model
- The basic Bertrand duopoly model of differentiated products is
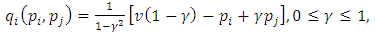
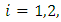 where
where 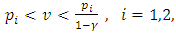 and where
and where 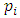 and
and 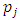 are, respectively, the prices set by duopolists i and j, and
are, respectively, the prices set by duopolists i and j, and 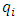 the resulting demand of duopolist i (e.g. [2, 9]).
the resulting demand of duopolist i (e.g. [2, 9]).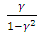 is the cross effect of
is the cross effect of 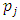 on
on 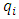 .
.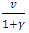 is the quantity demanded when prices are zero. Thus this quantity is between
is the quantity demanded when prices are zero. Thus this quantity is between 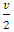 and
and 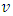 .
. 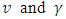 are assumed to be identical for both duopolists, so the model is symmetric. Now,
are assumed to be identical for both duopolists, so the model is symmetric. Now, 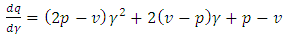 is positive if
is positive if 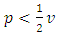 and
and 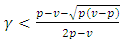 or if
or if 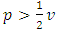 and
and 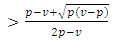 . Note that
. Note that  profit is
profit is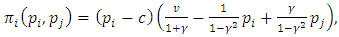 where
where 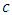 is the unit production cost, and
is the unit production cost, and 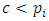
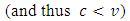 .
.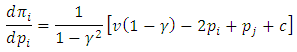
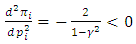 , so
, so  is concave in
is concave in  .Here the Nash-equilibrium is the solution of
.Here the Nash-equilibrium is the solution of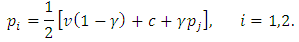 The symmetric solution
The symmetric solution 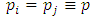 is thus
is thus 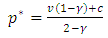 , which increases in
, which increases in 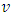 and
and 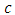 and decreases in
and decreases in 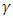 . (Note that since for a monopolist with this parametrization
. (Note that since for a monopolist with this parametrization 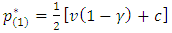 , therefore
, therefore 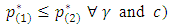
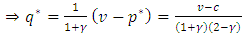 , which increases in
, which increases in 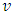 , decreases in
, decreases in 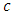 and increases in
and increases in 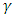 if
if 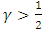
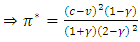 , which increases in
, which increases in 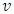 and decreases in
and decreases in 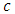 and
and 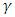 ; all are intuitive.For example, if
; all are intuitive.For example, if 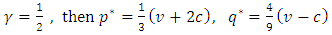 and
and 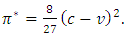
3. Three Firms
- Here the assumption is that
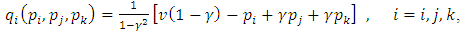 so the effect of other products’ prices on the demand of a product is symmetric (cf. [6]). So
so the effect of other products’ prices on the demand of a product is symmetric (cf. [6]). So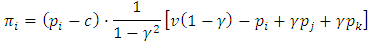 Denoting
Denoting 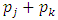 by
by 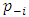 , we have
, we have 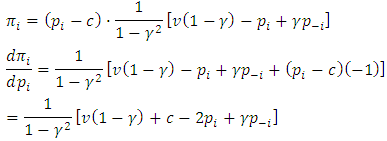
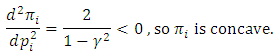 The optimality condition implies that
The optimality condition implies that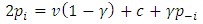 So the symmetric solution is
So the symmetric solution is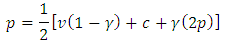 and thus
and thus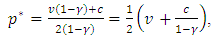 which increases in
which increases in 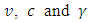 ,
, 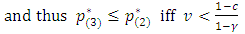 .
.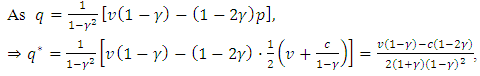 which increases in
which increases in 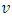 and decreases in
and decreases in 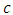
 Here are some relevant comparative statics.
Here are some relevant comparative statics.
4. Non-Linear Costs Duopoly
- Here
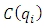 are the possibly, non-linear costs of duopolist
are the possibly, non-linear costs of duopolist 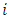 producing
producing 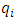 units, with
units, with 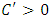 and
and 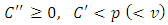 thus
thus 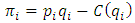
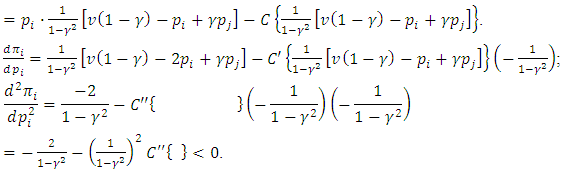 To obtain an explicit solution we need a specific (family of) function(s) C.Example
To obtain an explicit solution we need a specific (family of) function(s) C.Example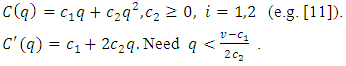
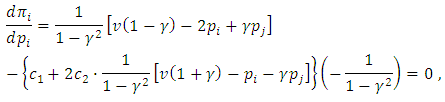 so
so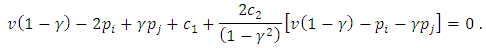 Thus
Thus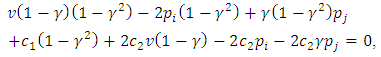 so
so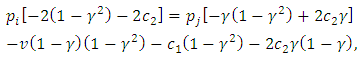 i.e.,
i.e.,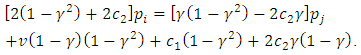 For the symmetric solution
For the symmetric solution 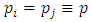
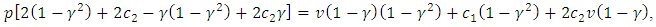 so we have:Proposition 1 For quadratic costs
so we have:Proposition 1 For quadratic costs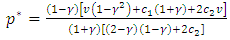 , which increases in
, which increases in 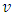 and
and 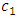 .
. 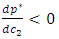 if
if 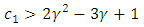 or
or 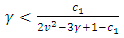 .Under this condition
.Under this condition 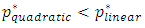
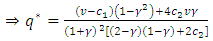 , which increases in
, which increases in 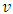 and decreases in
and decreases in 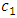 . It decreases in
. It decreases in 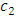 if
if 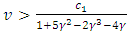 . Under this condition
. Under this condition 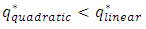
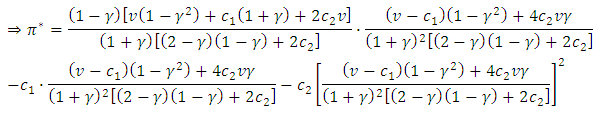 i.e.,
i.e.,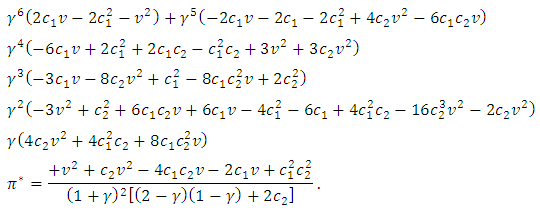 It is possible to demonstrate that if
It is possible to demonstrate that if 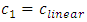 then
then 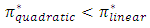 .
.5. With Reference Price(s)
- See Güler et al. [8] and Popescu and Wu [7] for suggestions for incorporating reference prices in supply chain models, motivated by Marketing and Psychological studies (e.g. [12, 13] that found it to be prevalent in (consumer) behavior.Let
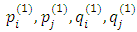 be the prices and quantities in period 1, and similarly for period 2.2nd period:The demand model for the second period(*) is
be the prices and quantities in period 1, and similarly for period 2.2nd period:The demand model for the second period(*) is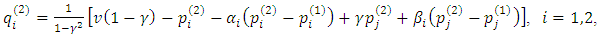 where
where 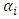 is the effect of own price change, and
is the effect of own price change, and 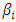 , the effect of competitor's price change. We shall assume that
, the effect of competitor's price change. We shall assume that 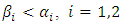 .Note that if
.Note that if 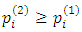 and
and 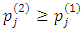 the contribution of the first reference-price difference is negative, and of the second positive. If
the contribution of the first reference-price difference is negative, and of the second positive. If 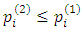 and
and 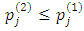 , the signs of these contributions reverse, but the expressions remain the same.Also,
, the signs of these contributions reverse, but the expressions remain the same.Also, 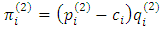 [noise has no effect]. Thus
[noise has no effect]. Thus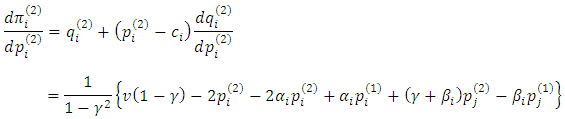 Proposition 2In the symmetric case
Proposition 2In the symmetric case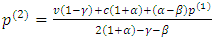 . Note that the denominator is positive since
. Note that the denominator is positive since 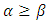 and
and 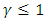 .
.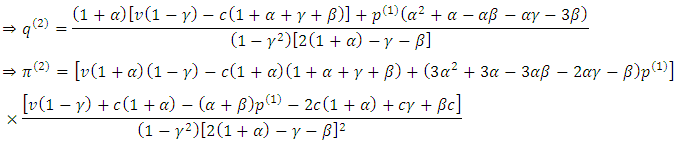 As for comparative statics,
As for comparative statics, 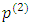 is linear in
is linear in 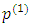
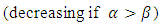 . It is increasing in v and c.
. It is increasing in v and c.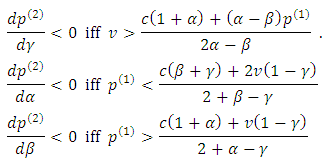 Or, in different form, if
Or, in different form, if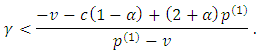
 increases in
increases in  and decreases in
and decreases in 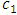 .Now, moving to the first period,
.Now, moving to the first period, 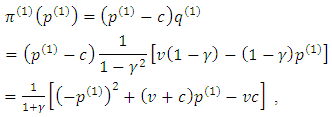 and
and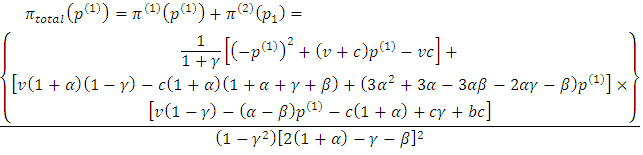 As the denominator is independent of
As the denominator is independent of 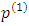 , and positive, we shall focus on the numerator.It can be shown that
, and positive, we shall focus on the numerator.It can be shown that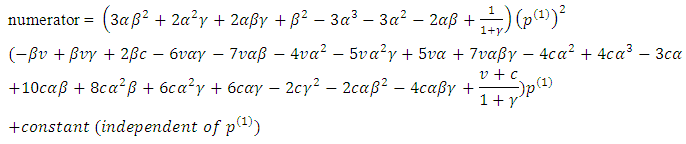 Thus
Thus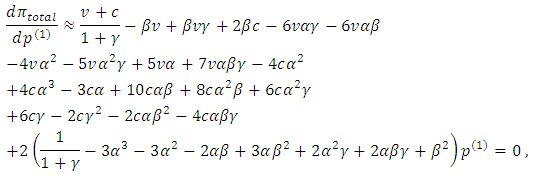 where
where 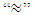 means “has the same sign as”.So
means “has the same sign as”.So 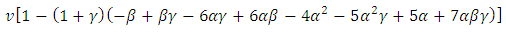
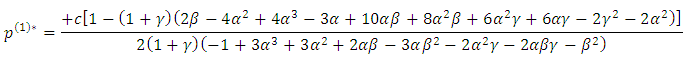
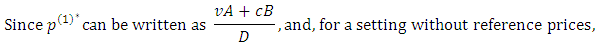
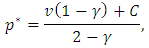 sufficient conditions for
sufficient conditions for 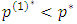 are
are 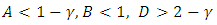 . These conditions hold with some restrictions on the parameters.
. These conditions hold with some restrictions on the parameters.6. Concluding Remarks
- We generalized the basic Bertrand model of differentiated duopoly in three ways: 1. Extension from two firms to three (tri-opoly). 2. Extension from linear to non-linear (convex) production costs (with two and three firms). 3. Extension to a two-period model where demand in the second depends also on the price in the first (reference price). Note that the term "reference effects" is used in some literature when the price of a product influences one's attitude to the price of another (e.g., [14]) which is a totally different meaning than our temporal "reference effect".The tri-opolists are shown to charge, under certain conditions, higher price than the duopolists (who charges a higher price than a monopolist). For non-linear costs, we used a quadratic function. We provide complete comparative statics.Our reference price model assumes that demand in the second period depends on one's own price difference and competitor's price difference between periods one and two. We find the optimal price and profit in the second period (as a function of the price in the first), then add to it the profit in the first period (which is also a function of the price in that period) and then optimize the sum over that price.One possible extensions is to embed non-linear production costs in the reference price model.One other possible generalization of the Bertrand model and its extensions is to assume a non-linear demand model, like
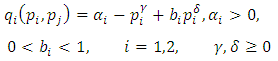 (e.g. [15] and references therein).Another direction is the extension of the reference price model to more than two periods (for a continuous time model where demand always also depends on the price at time zero, see Fibich et al. [16]).
(e.g. [15] and references therein).Another direction is the extension of the reference price model to more than two periods (for a continuous time model where demand always also depends on the price at time zero, see Fibich et al. [16]).Note
- (*) For the first period, we still have
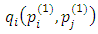 as in the basic model.
as in the basic model. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML