-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2016; 5(2): 42-44
doi:10.5923/j.jgt.20160502.02

Riesz Decomposition of Fuzzy Coalition Functions
Murat Beşer
Department of Economics, Agri Ibrahim Cecen University, Agri, Turkey
Correspondence to: Murat Beşer, Department of Economics, Agri Ibrahim Cecen University, Agri, Turkey.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this work, it is shown that when fuzzy measure set which has cone structure is closed, generating and norm normal, it obtains Riesz decomposition. Thus, it is indicated that each fuzzy measure can be stated as the linear combination of non-monotonic fuzzy measures.
Keywords: Non-monotonic fuzzy measure, Banach space, Riesz decomposition
Cite this paper: Murat Beşer, Riesz Decomposition of Fuzzy Coalition Functions, Journal of Game Theory, Vol. 5 No. 2, 2016, pp. 42-44. doi: 10.5923/j.jgt.20160502.02.
1. Introduction
- Murofushi [1] had introduced the fuzzy measurement concept that is not monotone by removing monotonousness characteristics defined on fuzzy measurements and examined the features that belong to a special subset that has bounded variation feature of these measurements in his study. In Jang and Kwon’s [2] study, they had extended Murofushi’s assumptions with the help of the
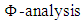 based on bounded variation that Schramn [3] had presented. Narukawa [4] had examined the features of convergence in Banach space that non-monotonic bounded variation structured measurements had generated. In this study, features of the cone structure created by the fuzzy measurements that had bounded variation feature had been examined and it had been indicated that it had the Riesz decomposition characteristic. Thus, it had been showed that every fuzzy measurement could be expressed as the combination of the non-monotonic characteristics.
based on bounded variation that Schramn [3] had presented. Narukawa [4] had examined the features of convergence in Banach space that non-monotonic bounded variation structured measurements had generated. In this study, features of the cone structure created by the fuzzy measurements that had bounded variation feature had been examined and it had been indicated that it had the Riesz decomposition characteristic. Thus, it had been showed that every fuzzy measurement could be expressed as the combination of the non-monotonic characteristics. 2. Non-Monotonic Fuzzy Measure Spaces
- Let X be defined as non-empty set and
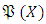 be defined as the measurable space for
be defined as the measurable space for 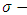 algebra
algebra 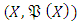 that is described on this set. Definition 2.1: If
that is described on this set. Definition 2.1: If 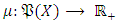 set function which is defined on measurable space
set function which is defined on measurable space 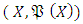 provides the following characteristics, it is described as the fuzzy measurement.
provides the following characteristics, it is described as the fuzzy measurement.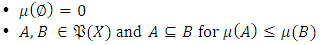 Definition 2.2: If
Definition 2.2: If 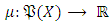 set function which is defined on measurable space
set function which is defined on measurable space 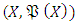 provides the
provides the 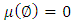 characteristic, it is described as the non-monotonic fuzzy measurement.It is clear that
characteristic, it is described as the non-monotonic fuzzy measurement.It is clear that 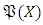 has generated chain of
has generated chain of 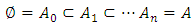 under the coverage relation of the subsets belonging to it. Every sequential element of the chain
under the coverage relation of the subsets belonging to it. Every sequential element of the chain 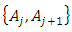 has composed a relation and hereby chain structure has appeared as the combination of the sequential elements. Definition 2.3: Total variation value
has composed a relation and hereby chain structure has appeared as the combination of the sequential elements. Definition 2.3: Total variation value 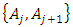 that belongs to non-monotonic fuzzy measurement function
that belongs to non-monotonic fuzzy measurement function 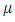 defined on the measurable space
defined on the measurable space 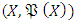 is described for a linkage as
is described for a linkage as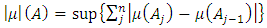 | (1) |
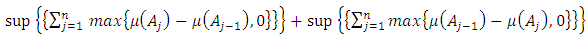 | (2) |
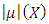 expression for
expression for 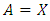 has been showed with
has been showed with 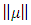 and it is defined as the bounded variation for
and it is defined as the bounded variation for 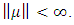 Let fuzzy measurements set be given as
Let fuzzy measurements set be given as 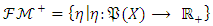 . The set of
. The set of 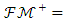
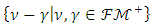 has a closed structure for every
has a closed structure for every 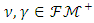 and it has generated linear space. Although the subset
and it has generated linear space. Although the subset 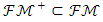 generates the positive cone structure in related linear space. If non-monotonic fuzzy measurement function
generates the positive cone structure in related linear space. If non-monotonic fuzzy measurement function 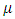 has bounded variation,
has bounded variation, 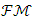 is the element of the linear space. The opposite of this suggestion is also true. (Aumann and Shapley, 1974:27)We can describe the norm of
is the element of the linear space. The opposite of this suggestion is also true. (Aumann and Shapley, 1974:27)We can describe the norm of 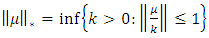 defined on the linear space of
defined on the linear space of 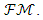 It has been known that the inequality of
It has been known that the inequality of 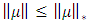 is valid for
is valid for 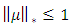 [5].Theorem 2.1:
[5].Theorem 2.1: 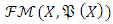 has generate the norm structure
has generate the norm structure 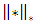 that is defined on the linear space and
that is defined on the linear space and 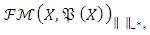 has the Banach space structure. Proof: (Jang and Kwon, 1997:104,105) and (Schramn, 1985) had described the related proof for
has the Banach space structure. Proof: (Jang and Kwon, 1997:104,105) and (Schramn, 1985) had described the related proof for 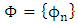 increasing convex functions series as the
increasing convex functions series as the 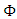 –bounded variation structure. Privately, if we describe the
–bounded variation structure. Privately, if we describe the 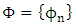 series for every
series for every 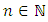 as
as 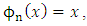 bounded variation structure is obtained. It is clear that the cone of
bounded variation structure is obtained. It is clear that the cone of 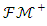 has the closed cone characteristic according to
has the closed cone characteristic according to 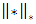 norm in the Banach space
norm in the Banach space 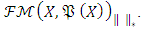 Definition 2.4: Let
Definition 2.4: Let  be Banach space and
be Banach space and 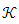 be the closed cone defined in this space. Closed cone
be the closed cone defined in this space. Closed cone 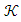 has the powerful Levi characteristics if every
has the powerful Levi characteristics if every 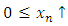 increasing sequence that is defined in
increasing sequence that is defined in 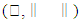 provides norm convex feature for
provides norm convex feature for 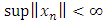 [6].Theorem 2.2: Let
[6].Theorem 2.2: Let 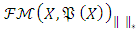 be given for Banach space and
be given for Banach space and 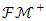 be given for closed cone belonging to this space. If cone
be given for closed cone belonging to this space. If cone 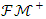 has powerful Levi characteristic, it has also the norm normality feature at the same time. Definition 2.5: Let
has powerful Levi characteristic, it has also the norm normality feature at the same time. Definition 2.5: Let 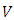 be linear space and
be linear space and 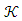 be the cone in this space. If the equality of
be the cone in this space. If the equality of 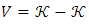 is valid,
is valid, 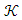 is defined as the generating cone. From the definition, it is clear that
is defined as the generating cone. From the definition, it is clear that 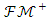 cone is the generating cone of
cone is the generating cone of 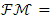
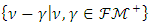 linear space.Let
linear space.Let 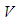 be given as the
be given as the 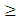 order relation (reflexive, transitive, anti-symmetric) on the linear space. When
order relation (reflexive, transitive, anti-symmetric) on the linear space. When 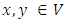 and
and 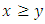 were given, it is defined as the
were given, it is defined as the 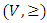 ordered vector space if the following conditions are satisfied.
ordered vector space if the following conditions are satisfied.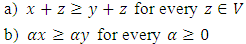 It is clear that
It is clear that 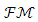 linear space has the ordered vector space characteristic. Definition 2.6: Let
linear space has the ordered vector space characteristic. Definition 2.6: Let 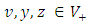 be given in the (V,≥) ordered vector space. If this space has Riesz decomposition characteristic, there are such
be given in the (V,≥) ordered vector space. If this space has Riesz decomposition characteristic, there are such 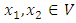 elements for the inequality
elements for the inequality 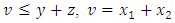 can be written under the conditions of
can be written under the conditions of 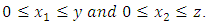 When data features had been provided for the given two theorems Banach space and
When data features had been provided for the given two theorems Banach space and 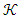 cone embedded into it in the rest of study, related space has showed that it satisfies the Riesz decomposition characteristic. Theorem 2.3 [7] Let be Banach space and
cone embedded into it in the rest of study, related space has showed that it satisfies the Riesz decomposition characteristic. Theorem 2.3 [7] Let be Banach space and 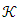 cone that is defined in this space be closed, generating and normal structured. Banach space should provide the following feature to have the Riesz decomposition characteristic.Ÿ Let at most three vectors be for providing the
cone that is defined in this space be closed, generating and normal structured. Banach space should provide the following feature to have the Riesz decomposition characteristic.Ÿ Let at most three vectors be for providing the 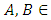
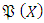 and
and 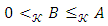 sequence. In this case, the elements
sequence. In this case, the elements 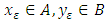 for every
for every 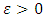 can be found as satisfying the conditions
can be found as satisfying the conditions 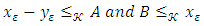 under the assumption of
under the assumption of 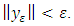 Theorem 2.4 [8] If is ordered Banach space and
Theorem 2.4 [8] If is ordered Banach space and 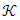 cone which is defined in this space is closed, generating, norm normal structured cone, it has the following characteristics.Ÿ Banach space has the Riesz decomposition characteristic.Ÿ The dual of Banach space is Riesz space.Ÿ The dual of Banach space has the Riesz decomposition characteristic.It had been showed that
cone which is defined in this space is closed, generating, norm normal structured cone, it has the following characteristics.Ÿ Banach space has the Riesz decomposition characteristic.Ÿ The dual of Banach space is Riesz space.Ÿ The dual of Banach space has the Riesz decomposition characteristic.It had been showed that 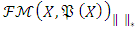 ordered Banach space and
ordered Banach space and 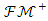 cone that belongs to this space have closed, generating and norm normal characteristics. With the help of the Theorem 2.3, it is clear that
cone that belongs to this space have closed, generating and norm normal characteristics. With the help of the Theorem 2.3, it is clear that 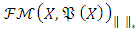 Banach space has Riesz decomposition characteristic so
Banach space has Riesz decomposition characteristic so 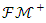 cone has it. This case has indicated that every
cone has it. This case has indicated that every 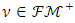 fuzzy measurement can be expressed with the help of non-monotonic fuzzy measurements.
fuzzy measurement can be expressed with the help of non-monotonic fuzzy measurements. 3. Conclusions
- It had been revealed that the cone structure formed by fuzzy measurements which were defined in the ordered Banach space that non-monotonic fuzzy measurements created has the Riesz decomposition characteristic under the closed, generating and norm normal structured feature thus fuzzy measurements can be expressed as the linear combination of the non-monotonic fuzzy measurement.
Notes
- 1. The set
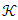 defined on the
defined on the 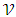 linear space is described as the cone if it provides the following conditions.
linear space is described as the cone if it provides the following conditions.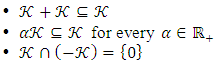 2.
2. 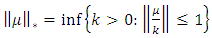 norm that is defined on the Banach space
norm that is defined on the Banach space 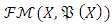 is equivalent to the
is equivalent to the 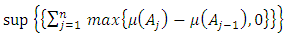
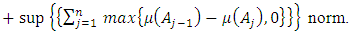 3.
3. 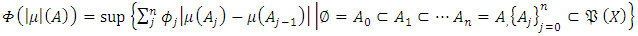 4.
4. 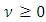 inequality is valid if
inequality is valid if 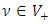
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML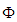 -Bounded Variation,” Fuzzy Sets and Systems, vol. 86, pp. 101-106, 1997.
-Bounded Variation,” Fuzzy Sets and Systems, vol. 86, pp. 101-106, 1997. -Bounded Variations and Riemann-Stieltjes Integration,” Transaction of American Mathematical Society, vol. 287, pp. 49-63, 1985.
-Bounded Variations and Riemann-Stieltjes Integration,” Transaction of American Mathematical Society, vol. 287, pp. 49-63, 1985.