Essam EL-Seidy1, Mohamed Mamdouh Zayet2, Hassan El-Hamouly2, E. M. Roshdy2
1Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt
2Department of Mathematics, Military Technical College, Cairo, Egypt
Correspondence to: Essam EL-Seidy, Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Game theory is an essential tool for a wide range of technologies. It has emerged as a powerful platform for business, economy, biology, military and many other fields. Recently, researchers have shown an increased interest in the behavior of strategies in a game under noise effect with short memory. The main challenge faced by many experiments is the great number of available strategies. So the study offers some important insights into two state automata. In the Iterated Prisoner's Dilemma (IPD) game, we display the interactions between the strategies which its reaction depends on the outcome of the round before the last one (strategies with memory two). With different average relatedness between players, we determine the payoffs matrices and illustrate the behavior of strategies under a probable error in implementation. We found that, Pavlov strategy is one of the superior strategies that can not be invaded.
Keywords:
Iterated games, Prisoner's dilemma, Finite automata, Game dynamics, Transition matrix, Perturbed payoff
Cite this paper: Essam EL-Seidy, Mohamed Mamdouh Zayet, Hassan El-Hamouly, E. M. Roshdy, Memory, Noise, and Relatedness Effect on Iterated Prisoner Dilemma Strategies Behaviour, Journal of Game Theory, Vol. 5 No. 1, 2016, pp. 16-26. doi: 10.5923/j.jgt.20160501.03.
1. Introduction
There is a growing body of literature that recognizes the importance of game theory. Game theory is frequently prescribed for conflict situations. Rational decision making has been studied by many researchers using the theory of games. Studies of Von Neumann [21] and Nash [20] showed the importance of game theory.Prisoner Dilemma (PD) could be considered one of the most frequently used example that arises in many applications [7, 24]. PD is a simple form of a two player-game. Each of the players has two choices, one of them is to cooperate C (deny) with the other player and the second is to defect D (confess). Both players are rewarded by R if both of them cooperate. In turn, they are punished by P if both of them defect [18, 22]. In the case of opposite decisions the co-operator is suckered by S and the defector is tempted by T.The conditions of PD are T > R > P > S, and 2R > T + S. The second condition means that the player who chooses mutual cooperation receives a payoff higher than switching between cooperation and defection [16]. This game can be summerized in the following payoff matrix.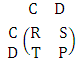 | (1) |
Game theory applications use groups of strategies for achieving goals. Surveys such that conducted by Rubinstein (1986) showed that the number of possible strategies grows exponentially with the number of rounds in the game [1, 6, 17, 18, 23]. Thus in Iterated Prisoner Dilemma (IPD) game, we have sixteen strategies (since, there exist four possible outcome R, S, T and P in each round). Each strategy action depend on the last round outcome. We denoted by Sk for these strategies of the two players; k = 0, 1, ......, 15. These strategies can be represented by a quadruple (u1, u2, u3, u4) of zeros and ones. Where ui denotes the probability to cooperate after outcome R, S, T and P respectively (pure strategies). Thus S15 = (1, 1, 1, 1) is the rule of cooperate in each round (AllC), S0 = (0, 0, 0, 0) is the rule of defect in each round (AllD) and S9 = (1, 0, 0, 1) for pavlov (Win Stay – Los Shift (WSLS)). These strategies can be pictured using two states automata [4, 10, 16]. Figure 1 represents the aoutomata of Tit For Tat (TFT).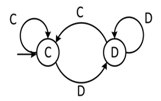 | Figure 1. Automata of TFT strategy |
A huge number of strategies is considered a common disorder characterized by a complexity and time consuming. The two state automata [9] plays a crucial role in regulating the huge number of existing strategies. So, the procedures of this study were approved by a finite two state automata. In this paper, we consider the interactions between the strategies which its reaction depends on the outcome of the round before the last one (strategies with memory two).There is only a few information about the effects of players’ relationship. So this paper traces the development of strategies’ behavior between the related players by increasing the players' payoff by a given factor. This factor depends on the relation between players. Game between relatives were reported in the first studies of Maynard Smith for the Hawk–Dove game [11, 14, 15]. Noise is an important component in the game theory and plays a key role in infinitely repeated games [18, 25]. Recently, investigators have examined the effects of a noise on (PD) game with memory one (the reaction depends on the outcome of the last round). Questions have been raised about the effect of noise on memory two [12] with relative players. In the pages that follow, it will be argued that the effect of error in implementation will be studied.In this paper, we will introduce a brief inkling of related players (PD) game. Then the payoff matrix will be computed with different values of relation factors under noise effect using memory two algorithm. Strategies behavior will be finally declared by analyzing the payoffs matrices.
2. Methodology
A case-study approach was adopted to help understanding how relative players cooperate. In recent years, two different approaches arises (personal fitness, inclusive fitness) have attempted into account for the payoff calculations. Personal fitness was prepared according to the procedure used by Grafen [14]. The data of this research were normalized using inclusive fitness approach [15]. Data management and analysis were performed using relatedness factor 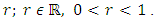 Traditionally, inclusive fitness has been assessed by increasing the player’s payoff by r times of the co-player payoff. Essam (2015) [9] identified the payoff matrix as follows:
Traditionally, inclusive fitness has been assessed by increasing the player’s payoff by r times of the co-player payoff. Essam (2015) [9] identified the payoff matrix as follows: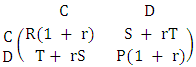 | (2) |
Case studies have been long established in (PD) game to present a detailed analysis of strategies behavior. Up till now, the research has tended to focus on memory one (PD) game [11, 14, 15, 18, 25]. This method is particularly useful in the study if the recent previous state is known. Memory two was prepared according to the procedure used by Essam (2016) [12]. Illustration 1 demonstrate how states will be produced using a conflict between S8 against S11.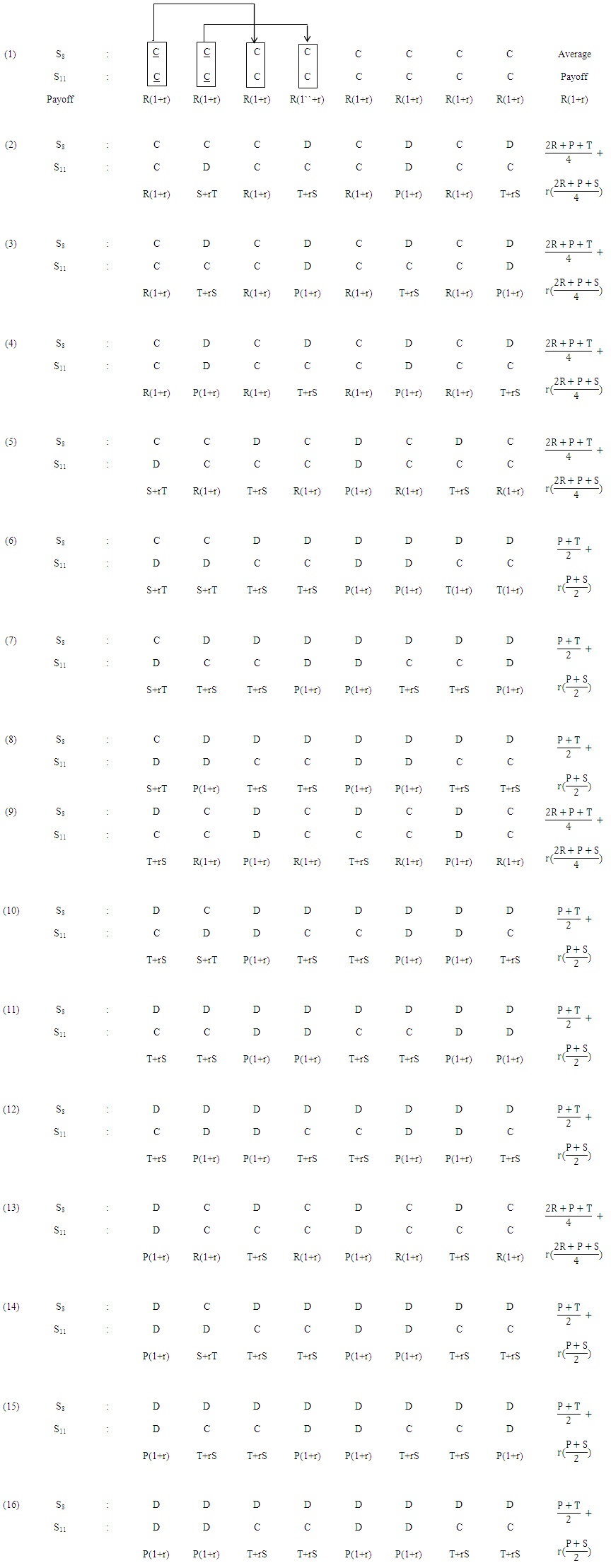 | Illustration 1. Confliction between S8 against S11 |
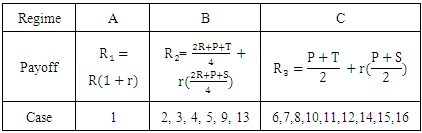
The sixteen alternatives raised in Illustration 1 yield only three average payoffs (regimes) as in Table 1.Table 1. Regimes of S8 against S11
 |
| |
|
In this investigation, there are several sources of error that may be occured. Error in implementation is the most frequent error. When error occurs, it may change the payoff of any rounds. Markov process is the main non-invasive method used to determine the transition matrix between available payoffs 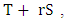
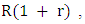
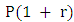 and
and 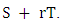 The first step in this process is to identify a couple of four quadruples P = (p1, p2, p3, p4) and Q = (q1, q2, q3, q4). P and Q represents the probability of playing C after the four possible outcomes
The first step in this process is to identify a couple of four quadruples P = (p1, p2, p3, p4) and Q = (q1, q2, q3, q4). P and Q represents the probability of playing C after the four possible outcomes 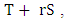
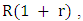
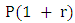 and
and 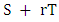 respectively. Once the four quadruples were constructed, the transition matrix takes place as follows:
respectively. Once the four quadruples were constructed, the transition matrix takes place as follows: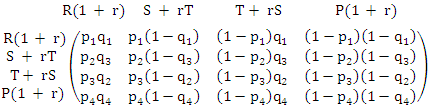 | (3) |
The previous matrix is of interest because it has a unique left eigenvector 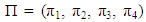 for eigenvalue 1. The eigenvector Π is the unique stationary distribution. Recent evidence suggests that stationary distribution is the probability to play C after every outcome if the game is repeated to infinity. Previous studies have reported that the perturbed payoff for player P against Q can be calculated by the following equation.
for eigenvalue 1. The eigenvector Π is the unique stationary distribution. Recent evidence suggests that stationary distribution is the probability to play C after every outcome if the game is repeated to infinity. Previous studies have reported that the perturbed payoff for player P against Q can be calculated by the following equation.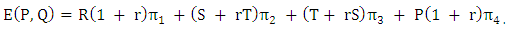 | (4) |
Since pi and qi are zeros or ones, then in some cases, the stochastic matrix (2) will contain many zeros, and it is no longer irreducible. Therefore, the vector π is no longer uniquely defined.Existing research calculates perturbed payoffs by a more simple, practical and direct approach. In the paragraph that follows, every regime of S8 against S11 will be studied separately.  Thus the corresponding transition matrix from one regime to another will be as follows.
Thus the corresponding transition matrix from one regime to another will be as follows. | (5) |
The triples 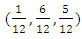 is the corresponding stationary distribution for perturbed S8 against S11. The perturbed payoff will be calculated by the following equation.
is the corresponding stationary distribution for perturbed S8 against S11. The perturbed payoff will be calculated by the following equation.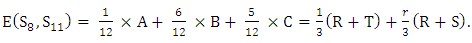 | (6) |
This algorithm will be repeated for every two strategies.Domination is the main invasive method to determine the strongest stable strategy. Does  dominates
dominates 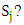 To answer this question, firstly four payoff values of
To answer this question, firstly four payoff values of 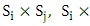
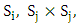 and
and 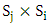 must be recalled. Then these payoffs are used to form a new 2×2 matrix.
must be recalled. Then these payoffs are used to form a new 2×2 matrix.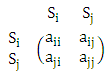 | (7) |
Then if 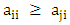 and
and 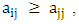 with at least one inequality being strict this means that
with at least one inequality being strict this means that 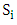 dominates
dominates 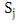 [17]. This algorithm will be repeated for each two strategies.
[17]. This algorithm will be repeated for each two strategies.
3. Results and Discussion
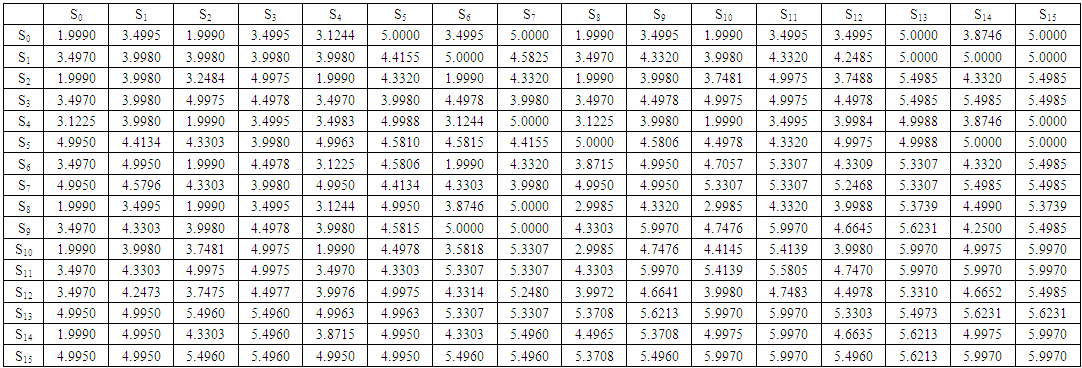
This set of analysis examines the impact of each strategy under the effect of average relatedness. This analysis takes place for different values of T, R, P, S, and r (Axelrod's values (T = 5, R = 3, P = 1, S = 0), Chicken game values (T = 1, R = 0, P = -10, S = -1), (T = 1, R = 5, P = 3,S = 0)) and is significant at r = 0.0001, and r = 0.999. So Table 8, Table 9, and Table 10 present an overview of these three cases. Every case has two states as follows:(1) The two states for Axelrod's values:i. One interesting finding for small average relatedness (r = 0.0001) at the first column in Table 8 is that every strategy is invaded by at least two strategies except S9. Strategy S9 (WSLS) not only neither strategy can invade it but also it outcompetes the greatest number of strategies (exactly twelve). This means that stategy S9 can be considered a strong strategy as in memory one. In addition, it is important to point out that S0 (AllD) and S8 (Grim) are also strong strategies which defeat eleven strategies. However S0 and S8 are strong strategies, they can't abide in front of S10 (TFT), which does well in front of defective strategies. On the other hand S6 (idiot) is an inactive strategy, which is defeated by twelve strategies and doesn't invade any strategy. It's also apparent that cooperative strategies such as S7, S14, and S15 are weak strategies which are invaded by eleven strategies at least. These results suggest that for small average relatedness defective strategies dominate cooperative ones.ii. The second column of Table 8 illustrates strategies’ behavior for large average relatedness (r = 0.999). From this data, it can be seen that S9 and S15 are superior strategies, as they don't permit any other strategy to rival them. Also, they put at least thirteen strategies down. In contrast to superior strategies, there are dormitive strategies S0, S6, and S7. These strategies are impermissible to beat any strategy. Also, there are twelve strategies that can crush S6. Overall, these results indicate that defective results fail in front of cooperative ones at large average relatedness.(2) Chicken game states:Surprisingly, no differences were found in strategies’ behavior between small and large average relatedness for all strategies in this case. Despite this, little progress has been made in the behavior of some strategies such as S11 (Tweedledee). Strategy S11 attacks nine strategies and forbids all other strategies to beat it. However S11 is a strong strategy, strategy S9 shows better results. Strategy S9 attacks five strategies more than S11. This means that S9 conquer all other strategies excep its strong competitor S11. Turning now to incompetent strategies such S0, S1, S6, and S7. Like the two states of Axelrod's values, S6 is the poorest strategy. Together these results provide important insights into the preponderance of cooperative strategies in the chicken game.(3) States of (T = 1, R = 5, P = 3, S = 0):In this case, there is no significant difference in strategies invasion between small and large r for all strategies except for S10. There are five strategies offense S10 for small r and six strategies for large r. Strategy S10 is invaded by S6 for large r only. This finding was unexpected because S6 is always an inactive strategy for the two previous cases. Moreover, S6 incommoding other three strategies and no strategy can wreaks it. As before S9 is the dominant which rashes six strategies. The evidence presented in this paragraph suggests that cooperative strategies scent defective ones.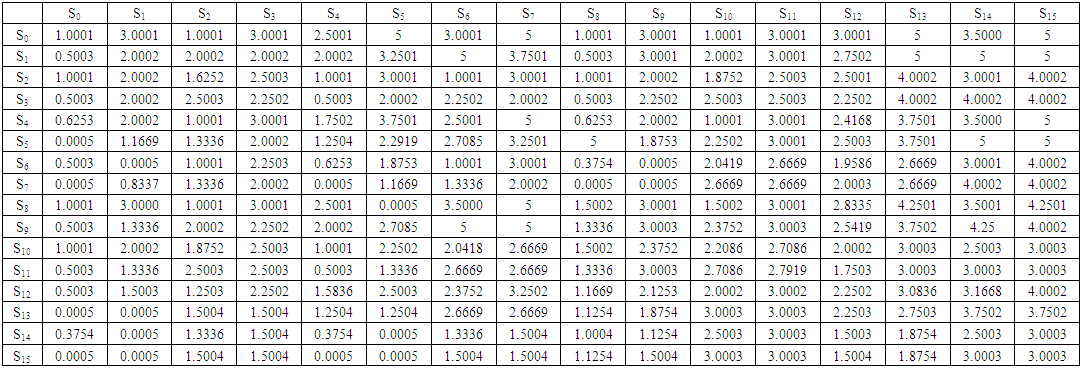 | Table 2. Payoff Matrix of Axelrod's Values (T = 5, R = 3, P = 1, S = 0) and r = 0.0001 |
 | Table 3. Payoff Matrix of Axelrod's Values (T = 5, R = 3, P = 1, S = 0) and r = 0.999 |
 | Table 4. Payoff Matrix of Values (T = 1, R = 0, P = -10, S = -1) and r = 0.0001 |
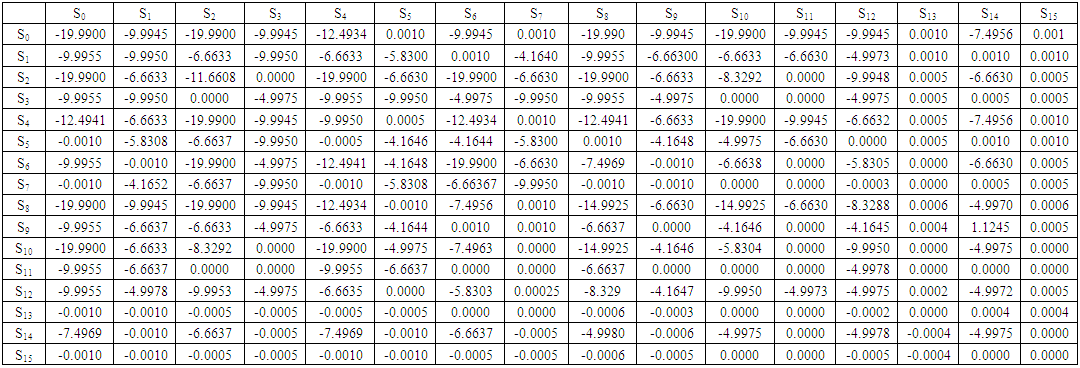 | Table 5. Payoff Matrix of Values (T = 1, R = 0, P = -10, S = -1) and r = 0.999 |
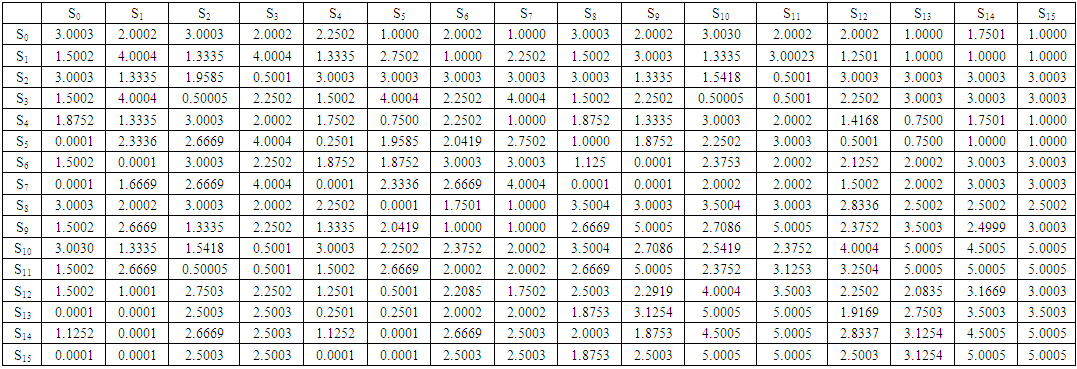 | Table 6. Payoff Matrix of Values (T = 1, R = 5, P = 3, S = 0) and r = 0.0001 |
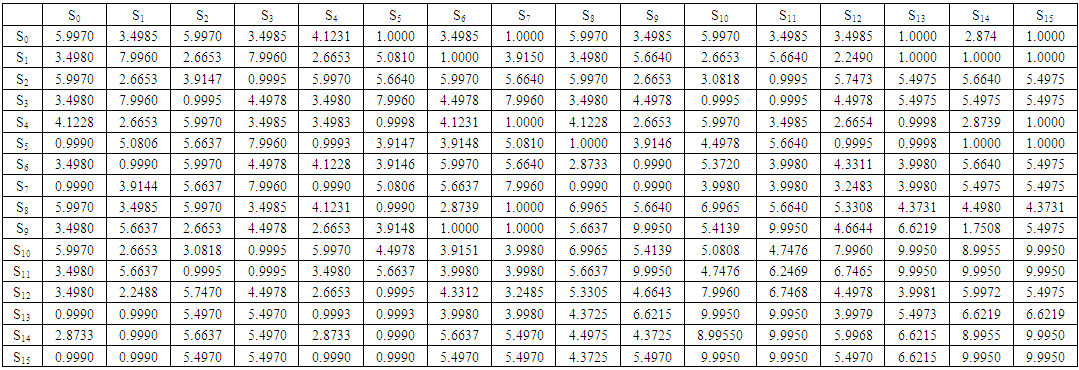 | Table 7. Payoff Matrix of Values (T = 1, R = 5, P = 3, S = 0) and r = 0.999 |
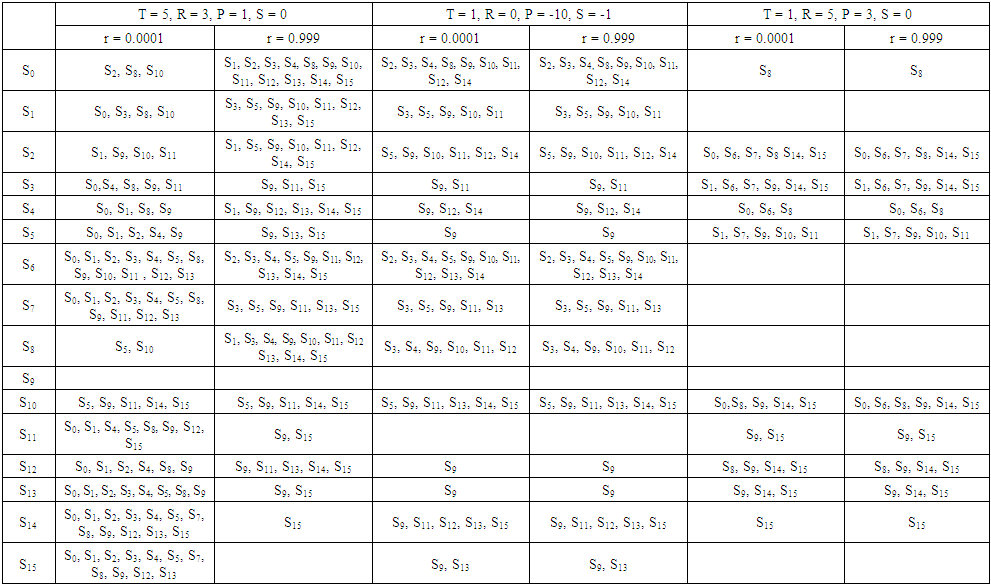 | Table 8. Dominating Strategies for Different Values of T, R, P, S, and r |
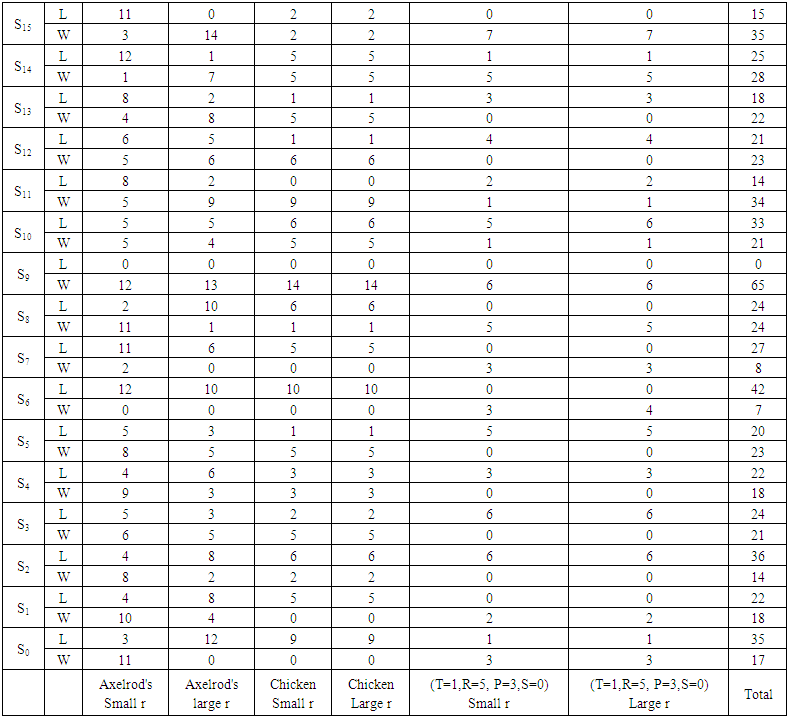 | Table 9. Number of Strategies which Outcompete (Lose (L)) Si or Outcompeted (Win (W)) by Si |
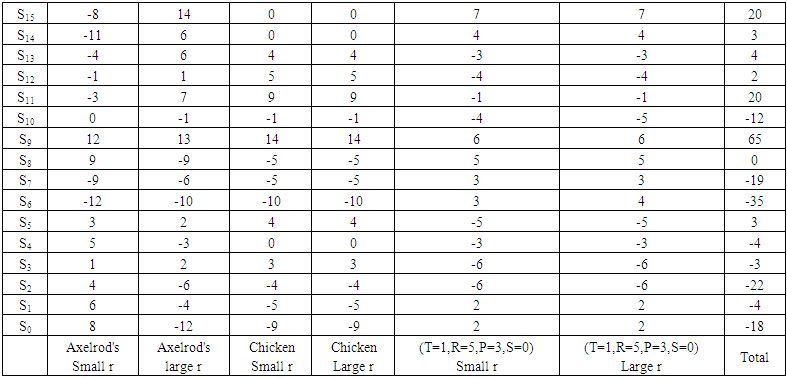 | Table 10. Difference between Number of Strategies that Outcompete Si and Outcompeted by Si |
4. Conclusions
The present study was designed to determine the effect of relatedness on strategies’ behavior between players of IPD game with memory two under noise effect. Only strategies generated by a finite two-state automata are used. The state before the last one is used to generate the new state instead of the immediately previous one. The outcome of the state before the last one is used due to the delay or lack of knowledge of the immediately previous one. This generation of states is affected by an error in implementation. If there is a relation between the players, any player can donates a fraction of its payoff to the other player. This fraction r takes values from zero to one. The payoff matrix is constructed and analyzed for different values of T, R, P, S, and r.Multiple regression analysis revealed that S9 has excellent performance. What is surprising is that there is no strategy that can withstand in front of S9 for all cases in Table 8. It is also apparent from Table 9 and Table 10 that S9 over press sixty-five opponents. So this study has identified that if any application can be modeled and played under the same conditions, it is advisable to use S9 anyway. One of the more significant findings to emerge from this study is to avoid playing with strategy S6. Strategy S6 renders in front of most strategies. Data from Table 9 reveal that S6 can't be standing in front of forty-two strategies. Also, Table 10 illustrates that the difference between the numbers of strategies that outcompete S6 and outcompeted by S6 is 35. In general, it seems that the player who plays with S6 will be the loser.
References
| [1] | D. Abreu, A. Rubinstein, The structure of Nash equilibrium in repeated games with finite automata, Economy. J. Econom. Soc. (1988) 1259–1281. |
| [2] | R.J. Aumann, Survey of repeated games, Essays Game Theory Math. Econ. Honor Oskar Morgenstern, Bibliogr. Institute, Mannheim/Wien/Zurich, (1981) 11–42. |
| [3] | R. Axelrod, The Evolution of Cooperation, Basic Books, New York. Econometrica. 39 (1984) 383–396. |
| [4] | R. Axelrod, W.D. Hamilton, The evolution of cooperation, Science (80-. ). 211 (1981) 1390–1396. |
| [5] | J.S. Banks, R.K. Sundaram, Repeated games, finite automata, and complexity, Games Econ. Behav. 2 (1990) 97–117. |
| [6] | K.G. Binmore, L. Samuelson, Evolutionary stability in repeated games played by finite automata, J. Econ. Theory. 57 (1992) 278–305. |
| [7] | R. Cressman, Evolutionary dynamics and extensive form games, MIT Press, 2003. |
| [8] | Z.K. E. El-Seidy, The perturbed payoff matrix of strictly alternating prisoner’s dilemma game, Far Fast J. Appl. Math. 2. 2 (1998) 125–146. |
| [9] | E.-S. Essam, The effect of noise and average relatedness between players in iterated games, Appl. Math. Comput. 269 (2015) 343–350. |
| [10] | E.-S. Essam, E.M. Elshobaky, K.M. Soliman, Two population three-player prisoner’s dilemma game, Appl. Math. Comput. 277 (2016) 44–53. |
| [11] | E.-S. Essam, S.H. Salah El Din, M.A. Ali, On The Behavior of Strategies in Iterated Games Between Relatives, (n.d.). |
| [12] | E.-S. Essam, M.M. Zayet, H. El-Hamouly, E.M. Roshdy, The Effect of Memory Change in Iterated Prisoner Dilemma Strategies Behaviour, J. Game Theory. 5 (2016) 1–8. |
| [13] | D. Fundenberg, E. Maskin, Evolution and cooperation in noisy repeated games, Am. Econ. Rev. (1990) 274–279. |
| [14] | A. Grafen, The hawk-dove game played between relatives, Anim. Behav. 27 (1979) 905–907. |
| [15] | W.G.S. Hines, J.M. Smith, Games between relatives, J. Theor. Biol. 79 (1979) 19–30. |
| [16] | L.A. Imhof, D. Fudenberg, M.A. Nowak, Tit-for-tat or win-stay, lose-shift?, J. Theor. Biol. 247 (2007) 574–580. |
| [17] | K. Lindgren, M.G. Nordahl, Evolutionary dynamics of spatial games, Phys. D Nonlinear Phenom. 75 (1994) 292–309. |
| [18] | K.S. Martin A. Nowak Essam El-Sedy, Automata, repeated games and noise, J. Math. Biol. 33 (1995) 703–722. |
| [19] | F. and Maskin, Evolution and repeated games, Mimeo. (2007). |
| [20] | J. Nash, Non-cooperative games, Ann. Math. (1951) 286–295. |
| [21] | J. von Neumann, O. Morgenstern, Theory of Games and Economic Behavior, Princeton University Press, Princeton, NJ. (1944). |
| [22] | A. Rapoport, A.M. Chammah, Prisoner’s dilemma: A study in conflict and cooperation, University of Michigan press, 1965. |
| [23] | A. Rubinstein, Finite automata play the repeated prisoner’s dilemma, J. Econ. Theory. 39 (1986) 83–96. |
| [24] | L. Samuelson, Evolutionary games and equilibrium selection. Series on economic learning and social evolution, (1997). |
| [25] | B.M. Zagorsky, J.G. Reiter, K. Chatterjee, M.A. Nowak, Forgiver triumphs in alternating Prisoner’s Dilemma, (2013). |



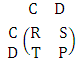

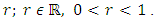 Traditionally, inclusive fitness has been assessed by increasing the player’s payoff by r times of the co-player payoff. Essam (2015) [9] identified the payoff matrix as follows:
Traditionally, inclusive fitness has been assessed by increasing the player’s payoff by r times of the co-player payoff. Essam (2015) [9] identified the payoff matrix as follows: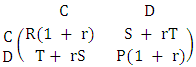

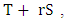
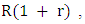
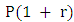 and
and 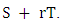 The first step in this process is to identify a couple of four quadruples P = (p1, p2, p3, p4) and Q = (q1, q2, q3, q4). P and Q represents the probability of playing C after the four possible outcomes
The first step in this process is to identify a couple of four quadruples P = (p1, p2, p3, p4) and Q = (q1, q2, q3, q4). P and Q represents the probability of playing C after the four possible outcomes 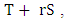
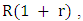
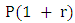 and
and 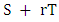 respectively. Once the four quadruples were constructed, the transition matrix takes place as follows:
respectively. Once the four quadruples were constructed, the transition matrix takes place as follows: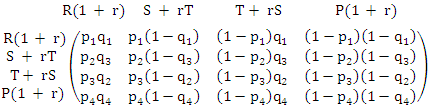
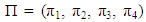 for eigenvalue 1. The eigenvector Π is the unique stationary distribution. Recent evidence suggests that stationary distribution is the probability to play C after every outcome if the game is repeated to infinity. Previous studies have reported that the perturbed payoff for player P against Q can be calculated by the following equation.
for eigenvalue 1. The eigenvector Π is the unique stationary distribution. Recent evidence suggests that stationary distribution is the probability to play C after every outcome if the game is repeated to infinity. Previous studies have reported that the perturbed payoff for player P against Q can be calculated by the following equation.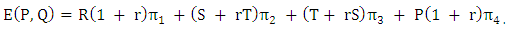
 Thus the corresponding transition matrix from one regime to another will be as follows.
Thus the corresponding transition matrix from one regime to another will be as follows.
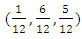 is the corresponding stationary distribution for perturbed S8 against S11. The perturbed payoff will be calculated by the following equation.
is the corresponding stationary distribution for perturbed S8 against S11. The perturbed payoff will be calculated by the following equation.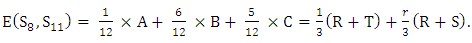
 dominates
dominates  To answer this question, firstly four payoff values of
To answer this question, firstly four payoff values of 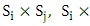
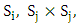 and
and 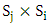 must be recalled. Then these payoffs are used to form a new 2×2 matrix.
must be recalled. Then these payoffs are used to form a new 2×2 matrix.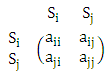
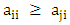 and
and 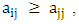 with at least one inequality being strict this means that
with at least one inequality being strict this means that 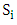 dominates
dominates 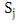 [17]. This algorithm will be repeated for each two strategies.
[17]. This algorithm will be repeated for each two strategies.








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML