1. Introduction

Game theory provides a quantitative framework for analyzing the behavior of rational players. The theory of iterated games in particular provides a systematic framework to explore the players' relationship in a long-term. It has been an important tool in the behavioral and biological sciences and it has been often invoked by economists, political scientists, anthropologists and other scientists who were interested in human cooperation ([1], [2], [11], [12]).

The evolutionary game theory has proven to be excellent for studying the evolution and success of different behavioral patterns in human as well as animal societies ([18]). The two games receiving the most attention are the hawk–dove and the Prisoner’s Dilemma game ([3]). In both games, the cooperative strategy, i.e. dove strategy in the hawk– dove game, warrants the highest collective payoff that is equally shared among the players. Mutual cooperation is, however, challenged by the defecting strategy, i.e. hawk strategy in the Hawk–Dove game, that promises the defector a higher income at the expense of the neighboring cooperator. The crucial difference that distinguishes both games is the way defectors are punished when facing each other. In the Prisoner’s Dilemma game, a defector encountering another defector still earns more than a cooperator facing a defector, whilst in the hawk–dove game the ranking of these two payoffs is switched. Thus, in the hawk–dove game a cooperator facing a defector earns more than a defector playing with another defector. This seemingly minute difference between both games has a rather profound effect on the success of both strategies. In particular, whilst by the Prisoner’s Dilemma spatial structure often facilitates cooperation this is often not the case in the hawk–dove game ([14]).

The Hawk-Dove game ([18]), also known as the snowdrift game or the chicken game, is used to study a variety of topics, from the evolution of cooperation to nuclear brinkmanship ([8], [22]). The basic idea of the Hawk-Dove (or chicken) game is that two opponents compete for a resource. The resource brings a benefit B to the one who wins it. In this game, opponents have the opportunity to play Hawk and fight (i.e., defect), or play Dove and give way (i.e., cooperate). The payoffs are maximized when both players give way and play Dove (cooperate). Unfortunately, in a world of doves, it pays to defect and play Hawk (defect). This game’s payoffs can be couched in terms of costs and benefits and modified to consider the joint consequences of kin selection and reciprocal altruism. Fighting is, however, dangerous and the looser of a fight has to bear a cost C. If a Hawk meets a Hawk, they will fight and one of them will win the resource. Thus, the average payoff of a Hawk meeting a Hawk is 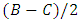. If a Hawk meets a Dove the Dove immediately withdraws, so its payoff is zero, while the payoff of the Hawk is B. If two Doves meet, the one who first gets hold of the resource keeps it while the other does not fight for it. Thus, the average payoff for a Dove meeting a Dove is 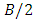. The strategic form of the game is given by the payoff matrix:

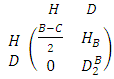(1)

In Nowak and Taylor ([23]), they studied five mechanisms for the evolution of the cooperative behavior in the prisoner’s dilemma game, direct and indirect reciprocity, kin selection, group selection, and network reciprocity. These mechanisms have been proposed to explain the evolution of cooperative behavior. The kin selection focuses on cooperation among individuals who are closely related genetically (Hamilton, 1964), whereas direct reciprocity focus on the selfish incentives for cooperation in repeated interactions ([4], [25]). The indirect reciprocity show how cooperation in larger groups can emerge when the cooperators can build a reputation. Network reciprocity operates in structured populations, where cooperators can prevail over defectors by forming clusters ([1], [19]).

Elseidy and Almuntaser ([27]) studied the evolution of cooperative behavior in Prisoner’s Dilemma game. They used a combination of mechanisms which allow the cooperation between the players to emerge and evolve, also they derived the fundamental conditions that makes the cooperative behavior evolutionary stable strategy. In this article, we use some combination of mechanisms to study the behavior of strategies in the Hawk-Dove game after we find the corresponding transformed matrix for each combination. We derive the necessary condition for evolution of fighting (play Hawk) or cooperation (play Dove) between players and evolutionary stability property (ESS) of the cooperative behavior and knowing that we intended to cooperate here both players will play Dove (give way). We derive the necessary conditions that make the hawks’ players risk- dominant (RD) and advantageous (AD) in a population in the context of the hawk-dove game.

2. Evolutionary Game Theory

The first ideas of evolutionary game theory showed up in the papers by Hamilton [13], Trivers [25], and Maynard Smith and Price [18]. Evolutionary game theory studies the behavior of large populations of agents who repeatedly engage in strategic interactions. Evolutionary game theory varies from classical game theory by concentrating more on the dynamics of strategy change as impacted not singularly by the nature of the various competing strategies, but by the impact of the frequency with which those various competing strategies are found in the population. Evolutionary game theory has turned out to be precious in clarifying numerous mind boggling and testing parts of science. It has been especially useful in building up the premise of altruistic behaviors inside of the connection of Darwinian procedure. In spite of its cause and unique reason, evolutionary game theory has become of increasing interest to economists, sociologists, anthropologists, and philosophers ([1], [7], [17]).

2.1. Evolutionarily Stable Strategies (ESS)

The idea of evolutionary stable strategies was defined and introduced by the British biologist John Maynard Smith and George R. Price in a 1973 ([20]). The idea is that one strategy in a given contest, on average, will win over any other strategy. The strategy ought to additionally have the advantage of doing great when set against adversaries utilizing the same strategy. This is important, because a successful strategy is likely to be common and the player will probably have to compete with others who are employing it. It does not have to be a single evolutionary strategy. It can be a combination of strategies, or a combination of players where every utilize only one strategy. Maynard Smith and Price specify two conditions for a strategy 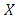to be an 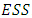. Either

I. 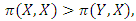that is, the payoff for playing 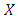against (another playing) 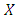is greater than that for playing any other strategy 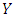against 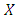for all

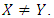Or

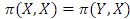II. and 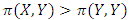, that is, the payoff of playing 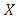against itself is equal to that of playing 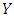against 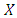but the payoff of playing 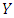against 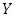is less than that of playing 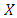against 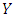for all

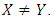Note that either (I) or (II) will do and that the previous is a more grounded condition than the recent. Clearly, if (I) gets, the Y invader commonly loses against X, and along these lines it can't even start to increase with any achievement. If (II) gets, the Y invader does as well against X as X itself, but it loses to X against other Y invaders, and therefore it cannot multiply. In short, 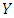players cannot successfully invade a population of X players. It is conceivable to present a strategy that is stronger than an 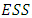, namely, an unbeatable strategy. Strategy 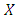is unbeatable if, given whatever other strategy :

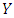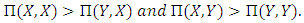An unbeatable strategy is the most powerful strategy, because it strictly dominates any other strategy; however it is additionally uncommon, and subsequently in exceptionally constrained use.

2.2. Evolutionary Game Dynamics

Evolutionary game dynamics is the application of population dynamical methods to game theory. It has been introduced by evolutionary biologists (such as William D. Hamilton and John Maynard Smith), anticipated in part by classical game theorists. Consider a game between two strategies, 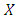and 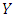, given by the payoff matrix:

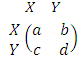(2)

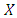The entries denote the payoffs for the row player. Thus, strategy obtains payoff a when playing another 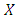player, but payoff b when playing a 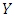player. Likewise, strategy 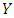obtains payoff c when playing an 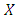player and payoff d when playing a 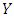player.

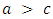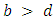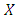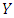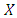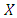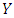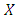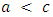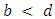1. If and , then dominates . In this case, it is always better to use strategy . The expected payoff of players is greater than that of players for any composition of a well-mixed population. is an unbeatable strategy in the sense of. If instead and , then 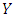dominates 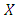and we have exactly the reverse situation .

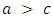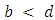2. If and , then both strategies are best replies to themselves, which leads to a ‘coordination game’. In a population where most players use 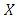, it is best to use 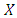. In a population where most players use 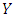, it is best to use 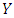. A coordination game leads to bi-stability: both strategies are stable against invasion by the other strategy.

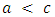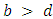3. If and , then both strategies are best replies to each other,

4. If 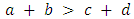then 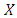is risk-dominant (RD). If both strategies are ESS, then the risk dominant strategy has the bigger basin of attraction.

5. If 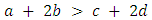then 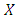is advantageous (AD).

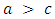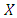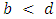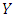6. If then is a strict Nash equilibrium. Likewise, if then is a strict Nash equilibrium. A strategy which is a strict Nash equilibrium is always an evolutionarily stable strategy (ESS) ([9], [23]).

2.3. ESS and Nash Equilibrium of the Hawk-Dove Game

Recall the Hawk-Dove game, Clearly, Dove is no stable strategy, since 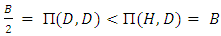, a population of doves can be invaded by hawks. Because of 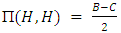and 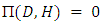, H is an ESS if 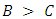. But what if 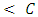? Neither H nor D is an ESS. But we could ask: What would happen to a population of individuals which are able to play mixed strategies? Maybe there exists a mixed strategy which is evolutionary stable.

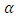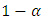Consider a population consisting of a species, which is able to play a mixed strategy, i.e. sometimes Hawk and sometimes Dove with probabilities and respectively. For a mixed ESS S to exist the following must hold:

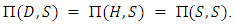Suppose that there exists an ESS in which H and D, which are played with positive probability, have different payoffs. Then it is worthwhile for the player to increase the weight given to the strategy with the highest payoff since this will increase expected utility. But this means that the original mixed strategy was not a best response and hence not part of an ESS, which is a contradiction. Therefore, it must be that in an ESS all strategies with positive probability yield the same payoff. Thus:

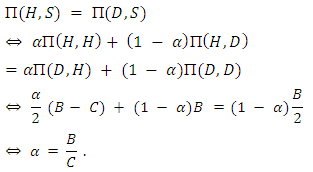Thus a mixed strategy with a probability 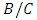of playing Hawk and a probability 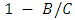of playing Dove is evolutionary stable, i.e. that it cannot be invaded by players playing one of the pure strategies Hawk or Dove.

To find the Nash equilibrium point of this game, Let 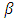be the probability of playing hawk if you are player 1 and let 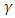be the probability of playing hawk if you are player 2. The payoffs to the two players are:

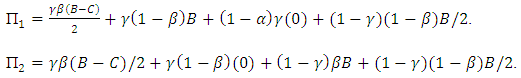Which simplifies to

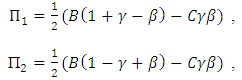Thus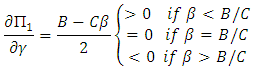

So the optimal 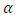is given by

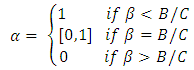Similarly,

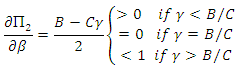So the optimal 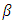is given by

This gives the diagram depicted in Figure 1. The best response functions intersect in three places, each of which is a Nash equilibrium. However, the only symmetric Nash equilibrium, in which the players cannot condition their moves on whether they are player 1 or player 2, is the mixed-strategy Nash equilibrium .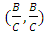

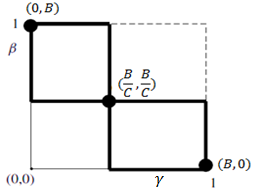Figure 1. Nash equilibria in the Hawk-Dove Game

3. Hawk-Dove Game among Kin Selection

Kinship theory is based on the commonly observed cooperative behaviors such as altruism exhibited by parents toward their children, nepotism in human societies, etc. Such behaviors toward one’s kin not only decrease the individual fitness of the donor (while benefiting the fitness of others), they often incur costs – thereby decreasing personal fitness.

Hamilton’s rule of relatedness provides the foundation of much of the work on kinship theory. This rule states that altruism (or less aggression) is favored when the following inequality holds:

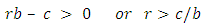where r is the genetic relatedness of two interacting agents, b is the fitness benefit to the beneficiary, and c is the fitness cost to the altruist. This rule suggests that agents should show more altruism and less aggression toward closer kin ([21]).

A simple way to study games between relatives was proposed by Maynard Smith for the Hawk- Dove game . In this section, we will study the Hawk-Dove game in which there is e relationship between the players. Consider a population where the average relatedness between players is given by r, which is a number between 0 and 1. There are two possible methods to study the games between relatives. The "inclusive fitness " method adds to the payoff of a player r times the payoff to his co-player. The personal fitness method, proposed by Grafen ([28]) modifies the fitness of the player by allowing for the fact that a player is more likely than other players of the population to meet co-player adopting the same strategy as himself. We regard the inclusive fitness method to study the Hawk-Dove game ([16] , [10] , [26]).

If we assume that there is a relationship between the players, then by using the inclusive fitness method, the payoff matrix of the Hawk-Dove game is given by:

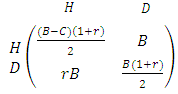(3)

We will analyze this model for stability of fighting (hawks’players) (ESS) , possibility of maintain the the Doves’players (cooperators) and when the fighting is risk-dominance (RD) and advantageous strategy (AD). From this transformed matrix, we get the following outcomes:

● The strategy of playing hawk (i.e defect strategy) will be ESS (evolutionary stable strategy), if:

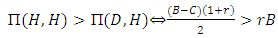Implies to .

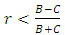● Hawk’player will be risk-dominant (RD) whenever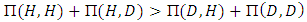

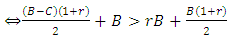Implies to

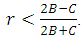● Hawk’playerwill be advantageous (AD) if:

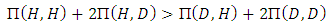i.e. if:

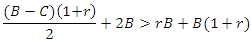Implies to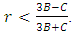

4. Hawk-dove Game among Direct Reciprocity

Direct reciprocity is considered to be a powerful mechanism for the evolution of cooperation, and it is generally assumed that it can lead to high levels of cooperation. Direct reciprocity has been studied by many authors ([25], [6]). Direct reciprocity is based on the idea ‘I help you and you help me’. In every round the two players must choose between cooperation and defection (fight of give way). With probability w there is another round. With probability 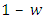the game is over. Consequently, the average number of interactions between two individuals is .

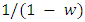In order to determine a fundamental condition for the evolution of cooperation in the repeated Hawk-Dove game, we can study the interaction between the dove who play with a strategy ‘always-defect’ (AllD) (i.e. Always cooperate and give away ) and the hawk who play with a strategy Tit -For- Tat (TFT). TFT starts with cooperation and then does whatever the opponent has done in the past move. On the off chance that two hawks (i.e. defectors) meet, they defect constantly. If two doves meet, they cooperate and give away all the time, so:

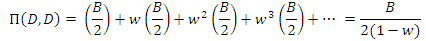If a hawk meets a dove, the TFT’player fighting in the first round and give away a short time later, while the AllD’player gives away in every round, so:

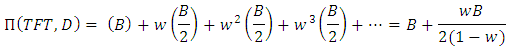While, the AllD’player will get

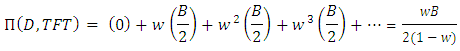And the two TFT’players will fight in all the interactions, so:

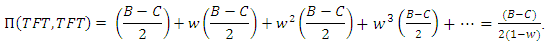Thus, the payoff matrix is given by:

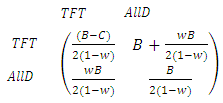(4)

● The TFT’players will be ESS if

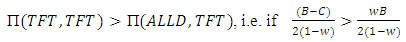Implies to

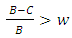(4.1)

Therefore, inequality (4.1) represents a base necessity for the evolution of fighting between players. If there are adequately numerous rounds, then direct reciprocity can prompt this behavior.

● The fighting will be risk-dominant (RD) whenever:

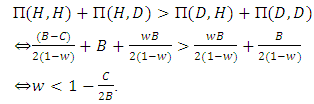● Fighting will be advantageous (AD) if: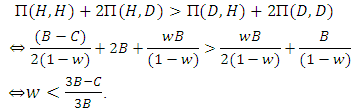

4.1. Direct Reciprocity with Kin Selection in Hawk-Dove Game

We will now consider that individuals use direct reciprocity with their relatives. One of the simplest strategies of direct reciprocity is Tit-For-Tat (TFT). We will consider that all the hawks are using TFT strategy while the doves are using AllD. Then, the payoff matrix is given by:

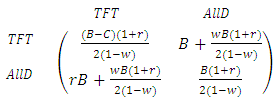(5)

From this matrix we get the following results :

● TFT will be stable against AllD’players if

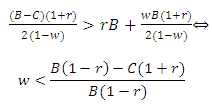● The fighting will be risk-dominant (RD) if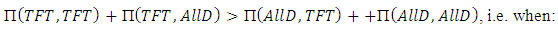

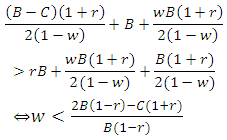● TFT’player has advantageous (AD) if:

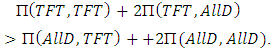i.e. whenever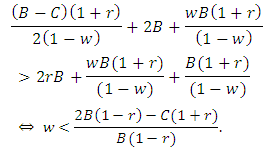

5. Group Selection among the Hawk-Dove Game

Selection does not only act on individuals, but also on groups. A group of cooperators might be more successful than a group of defectors. There have been many theoretical and empirical studies of group selection with some controversy, and most recently there is a Renaissance of such ideas under the heading of ‘multi-level selection’ ([5], [15], [24]).

A simple model of group selection works as follows: A population is subdivided into m groups. The maximum size of a group is n. Individuals interact with others in the same group according to a Hawk-Dove game. The payoff matrix that describes the interactions between individuals of the same group is given by:

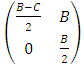(6)

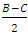Between groups there is no game dynamical interaction in our model, but groups divide at rates that are proportional to the average fitness of individuals in that group. The multi-level selection is an emerging property of the population structure. Therefore, one can say that fighting groups have a constant payoff , while the groups which give away have a constant payoff 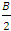. Hence, in a sense between groups the game can take the form as follows:

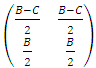(7)

For a large n and m, the essence of the overall selection dynamics on two levels can be described by a single payoff matrix, which is the sum of the matrix (6) multiplied by the group size, n, and matrix (7) multiplied by the number of groups, m ([21]). The result is:

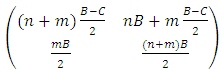(8)

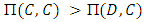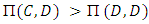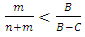The fighting will be stable if and hawks will invade doves if . If and 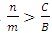respectively. Hawks are RD if 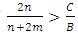and will be AD if .

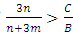5.1. Group Selection with Kin Selection in Hawk-Dove Game

We will now consider that there is a relationship between players in the same group, using the Hawk-Dove game, then the payoff matrix is given by :

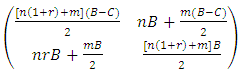(9)

From this transformed matrix we get the following conditions:

● The fighting strategy will be stable if

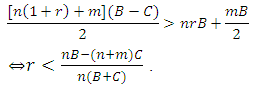● The fighting between relatives in the same group will be (RD) if the inequality:

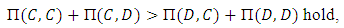Implies to

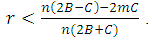● Also the fighting between relatives will be (AD) if:

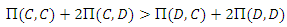i.e. when

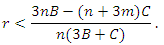Therefore, group and kin selection together can evolve strong fighting than either of them working alone, especially when average relatedness is low, groups are large and the number of groups is small.

6. Conclusions

Direct reciprocity can lead to the evolution of cooperative behavior (give way) but if it works together with kin selection it can lead to a strong cooperation between players . We found that, the necessary condition for evolution of cooperative behavior is:

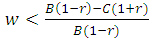, the population of cooperators will be RD if: 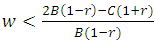. Where r is the average relatedness between individuals , which is a number between 0 and 1, and w is the probability of next round.

When the group selection works with kin selection, then our fundamental conditions, that we derived , showed that fighting can be maintained in the population, even when the average relatedness is low, groups are large and even if the benefits of fighting are low, if 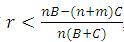, fighting between players can emerge, otherwise the cooperation (give way) behavior will be maintain in this situation. Hawks strategy will be risk-dominant (RD) whenever 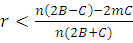, and will be advantageous (AD) if .

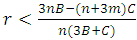For cooperation (give way) to prove stable, the future must have a sufficiently large shadow. An indefinite number of interactions, therefore, is a condition under which cooperation (give way) can emerge.