1. Introduction

Recent sequence of papers shows that computing one NE is PPAD (Polynomial Parity Arguments on Directed graphs)-complete for two, three, or four player games in strategic form [7] [8] [14] [15]. Chen and Deng [8] show that computing NE for two player games is PPAD-complete. Daskalakis et al [14] show that finding NE for four player games is PPAD-complete. Chen and Deng [7], and Daskalakis et al [15] independently show that calculating NE for three player games is PPAD-complete. All known algorithms require exponential time in the worst case. Chen et al [9] show that the problem of computing a 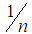- well supported NE in polymatrix games is PPAD-complete. Daskalakis and Papadimitriou [16] presented a polynomial time approximation scheme (PTAS) for 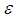-approximation NE in anonymous games. The authors described a PTAS for finding an 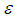-approximation NE in an anonymous game with two pure strategies with a certain order of running time. The PTAS in [16] depends on the existence of an 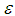-approximation NE consisting of integer multiples of 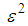. Daskalakis [13] presented improved PTAS from the running time view of point. This improved PTAS is based on the existence of an 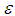-approximation NE satisfying the following conditions: either at most 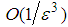players play mixed strategies, or al players who mix play the same mixed strategy. Daskalakis and Papadimitriou [17] extended the PTAS with any bounded number of pure strategies with running time 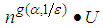for some function g of , number of pure strategies and , where U denotes the number of bits required to describe the payoff. Daskalakis and Papadimitriou's PTAS [13] [16] [17] are algorithms that enumerate a set of mixed strategy profiles which is independent of the input game as candidates for approximation NE, that is, the game is used only to verify if a given mixed strategy profile is an -approximation NE. The PTAS is called oblivious algorithms [18]. Daskalakis and Papadimitriou showed that these type of PTAS for anonymous games must have running time exponential in 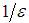. They also proposed a non-oblivious PTAS for two-strategy anonymous games. Chen et al [10] presented that the problem of computing a 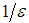-will-supported NE in a polymatrix game is PPAD-complete. Chen et al [9] showed that the problem of finding an 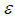-approximation NE in an anonymous game with seven pure strategies is PPAD-complete.

The application of fuzzy theory to decision making problems initiated by Bellman and Zadeh [2] in 1970. Butnariu [5] did fundamental research on fuzzy games. Chakeri and Sheikholeslam [6] show a method of finding fuzzy NE in Crisp and fuzzy games, Garagic et al [23] extend the concept of non cooperative game theory to fuzzy non cooperative games under uncertainty phenomena. Wu and Soo [35] applied fuzzy game theory to multi-agent coordination.

In this article, we use fuzzy theory as a tool to apply the fuzzy average to 2-player games. This paper represents a revised algorithm for computing mixed NE in 2-player games [20] [21]. This algorithm is based on the relationship between the expected payoff function of 2-player games and the mathematical representation of the fuzzy average of two linguistic values. Based on author’s understanding, the problem of computing mixed NE in 2-player games in normal form has not been proved in P-complete class. We prove that the new algorithm can compute mixed NE in 2-player games in polynomial time for any types of 2-player games in normal form. We claim that there is a fully polynomial time scheme of computing mixed NE in 2-player games in normal form.

This article is organized as follows. Section 2 discusses the preliminaries. Section 3 describes the algorithm for calculating mixed NE in 2-player games in details. Associated with the algorithm, a theorem, which indicates the main result in this article, and its proof are represented in this section. Section 4 provides examples. Section 5 is the conclusion and future study.

2. Preliminaries

2.1. 2-player Games in Normal Form

2-player games in normal form are also called bi-matrix games. A 2-player game is denoted by 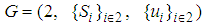, where, 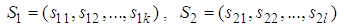is a set of strategies for player 1, player 2 respectively; the expected payoff function 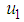of player 1, 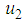of player 2 is as follows.

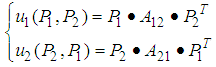(2.1)

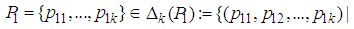
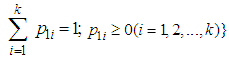where represents the probability distribution over 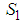; 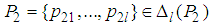represents the probability distribution over 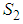; 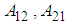is 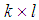payoff matrix, 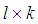payoff matrix, of player 1, player 2, respectively.

2.2. Optimal Values of Function f(x, y)

Let us review the Taylor expansion of a two variable function. Suppose that function f(x, y) is an infinitely differentiable, and (a, b) is a critical point of f(x, y), with 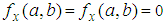. Function f(x, y)’s Taylor expansion is as follows.

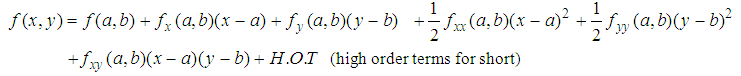In the case that (a, b) is a critical point, the first derivatives 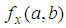and 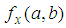are zero, the above equation becomes

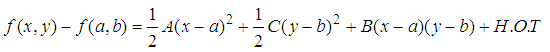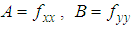where and 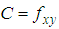. We can ignore the high order terms when (x, y) sufficiently close to (a, b). We rewrite the result as

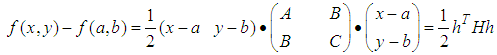(2.2)

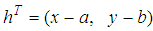where , the matrix H is called Hessian matrix, the representation on right hand is called quadratic form. 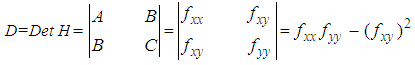is the determinant of Hessian matrix.

There are three cases we need to consider.

1. If (a, b) is local minimum value, then the right hand side of (2.2) must be positive for all (x, y) in a neighborhood of (a, b), such as for all (x, y) in a neighborhood of (a, b). Based on linear algebra, if the two eigenvalues of matrix H are positive, then .

2. If (a, b) is local maximum, then the right hand side of (2.2) must be negative, such as such as 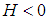for all (x, y) in a neighborhood of (a, b). Based on linear algebra, if the two eigenvalues of matrix H are negative, then .

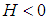3. If (a, b) is a saddle point, then the right hand side of (2.2) is either positive or negative depending on the values in neighborhood of (a, b). According to linear algebra, when two eigenvalues of matrix H are nonzero and have opposite sigh, point (a, b) is a saddle point.

The above inferences can be rephrased for two variable functions as follows.

1) If D > 0 and A > 0, then f(a, b) is a local minimum of f(x, y);

2) If D > 0 and A < 0, then f(a, b) is a local maximum of f(x, y);

3) If D < 0, then (a, b) is a saddle point of f(x, y);

4) If D = 0, then no conclusion can be drawn.

2.3. Fuzzy Numbers

A fuzzy number is a fuzzy set which is defined in R. There are some types of fuzzy numbers [27]. For example, triangular fuzzy numbers (TFNs), trapezoid fuzzy numbers, and etc. We only review TFNs in this paper.

The definition of a TFN:

A TFN is denoted as (a, b, c), where 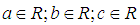and 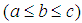. The TFN (a, b, c) is described in Figure 1.

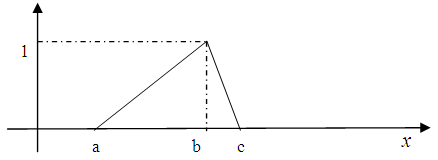Figure 1. Triangular fuzzy number (a, b, c)

The membership function of the TFN (a, b, c) is defined as

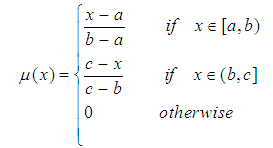There are two special TFNs. One is (a, a, c), such as a = b, and the other is (a, c, c), such as b = c. Suppose the membership function of TFN (a, a, c), (a, c, c) is 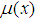, , 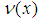respectively. Then one has the following.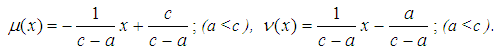

2.4. The Fuzzy Average

The fuzzy average [22] is defined with the average of linguistic values of a linguistic variable (x, T(x), U, G, M) [36] [37], where x the name of the variable; T(x) is the term set of x, U is the universe of discourse which is usually defined as interval [0, 1]; G is the syntactic rule which generates the terms in T(x); M is a semantic rule which is usually a mapping from the set T(x) to a set of fuzzy numbers defined in U. The fuzzy average of two values of a linguistic variable was described as follows.

Suppose that the two values of a linguistic variable are as follows. 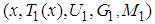and 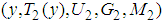, where , ; .

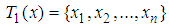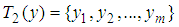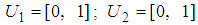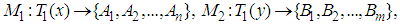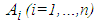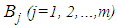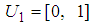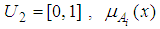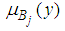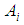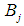where and are triangular fuzzy numbers (TFNs) which are defined on and and are the membership functions of TFNs and , respectively. The fuzzy average is defined as:

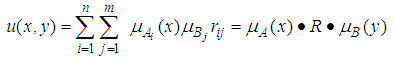where

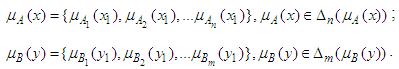
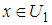and 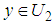; n is the number of entries in 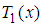; m is the number of entries in 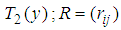is a 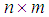matrix, which is called the consequence matrix [22]. It was proved that the fuzzy average converges to arithmetic mean under specific conditions [22].

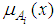is interpreted as the weight of element 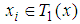. For a given 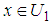and 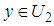, the vector 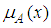, 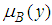is interpreted as probability distribution over 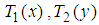, respectively.

In game theory, the set of strategies 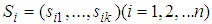can be interpreted as the term set 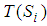in the concept of linguistic variables. For example, for a rock-scissors-paper game, a player’s strategy set 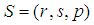can be considered as term set of {rock, scissors, paper} in linguistic variables, such as .

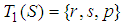For two player games in normal form, when player’s strategy set is represented by the term set, and the payoff matrix is same as the consequence matrix, it was proven that the expected payoff function is identical to the fuzzy average [20].

3. The Algorithm of Computing Nash Equilibria in 2-Player Games

This new algorithm is an extension of the algorithm [20] [21] for 2-player games. The main idea is the relationship between the expected payoff function of 2-player games in strategic form and the concept of the fuzzy average. Paper [20] proved that the expected payoff function of 2-player games in strategic form is identical to the fuzzy average of two linguistic values when the strategy sets in 2-player games are represented with the term sets in linguistic variables, the payoff matrix is replaced with the consequence matrix, and the probability distribution over strategy set for each player is represented with the semantic rule M in linguistic variables. The algorithm in this paper improves the algorithm which was published in [20] from the point of simplicity. The requirement of dividing strategy domains is no longer required for 2-player games in normal form. The algorithm is as follows.

1. For a given 2-player game in normal form, one needs to build two linguistic values .

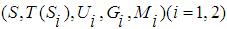1) Define the term sets by using the strategy sets, such as .

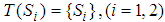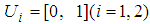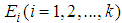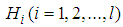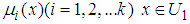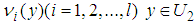2) Define , and suitable TFNs and , and their membership functions and , respectively.

3) Define proper semantic rules 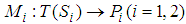where 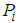is defined as

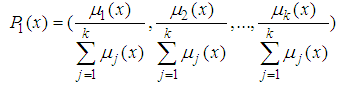(3.1)

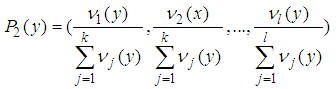(3.2)

It is clear that and .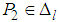

2. Construct the expected payoff function (2.1) by using the given payoff matrices, and the probability distributions which are defined in (3.1) and (3.2).

3. Solve (3.3).

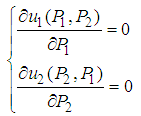(3.3)

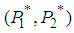4. Verify that the solution of (3.3) satisfies the conditions:

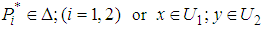5. Examine the point 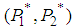by using Hessian matrix as follows.

5.1. For 2-player games, one can calculate the following.

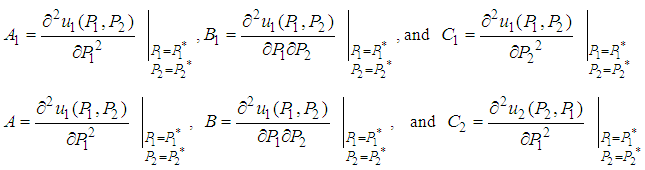5.2. Calculate .

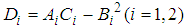If 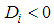, then 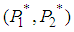is a saddle point of ;

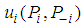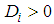If and 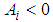, then, 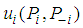reaches a local maximum value at ;

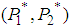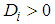If and 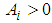, then 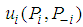reaches a local minimum value at ;

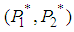If 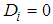, then no decision can be made.

This algorithm is able to calculate mixed NE in 2-player games within polynomial time. We give the following theorem.

Theorem 1

For a given 2-player game in normal form, when probability distributions of player 1 and player 2 are defined with (3.1) and (3.2), then the algorithm can find mixed NE in the 2-player game in polynomial time.

If we can prove that (3.3) becomes a system of linear equations, then the theorem is proved [3].

Proof:

When 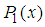and 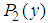are defined with (3.1) and (3.2), then (3.3) becomes the following.

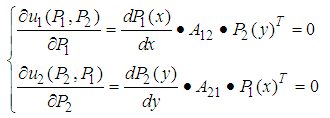(3.4)

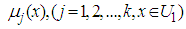According to the property of TFNs, we can define and 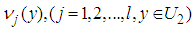as follows.

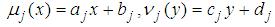, where 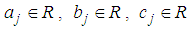and 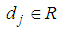are constant.

Then the sum of 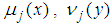is calculated respectively.

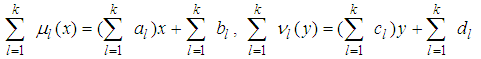(3.1) and (3.2) become as follows.

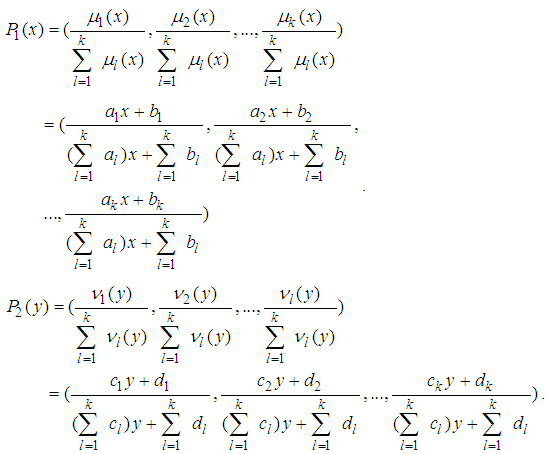Then the derivative of 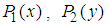is the following.

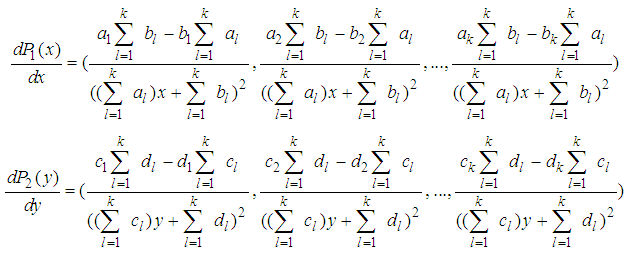It is clear that the elements in each derivative vector have common denominator, the numerator of each element in the above derivative vectors is a constant. On the other hand, the elements in vector 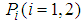have common denominator, and the numerator of each element in vector 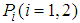is a piecewise linear function. Because we can ignore the common denominators in each equation of (3.4), then the first equation in (3.4) finally becomes a linear equation of y, the second equation in (3.4) becomes a linear equation of x. Therefore, equation (3.4) becomes a system of linear equations of x and y. Q.E.D.

4. Examples

Three examples are described in this section.

Example 1 - Rock- Scissors-Paper game. Find mixed NE for a Rock-Scissors-Paper Game with the following payoff bi-matrix.

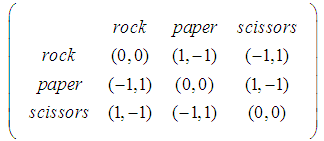This is a 2-player symmetric game. The payoff matrices of player 1 and player 2 are as follows.

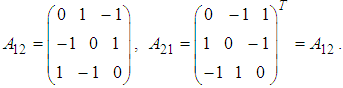We build two linguistic values 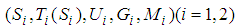. 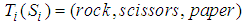, , 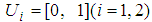and semantic rule 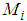is defined as follows.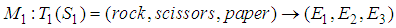

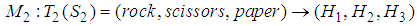, where is a TFN defined in , respectively.

We define 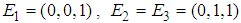and 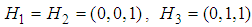. Then, the sum of membership functions 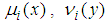of 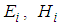is as follows.

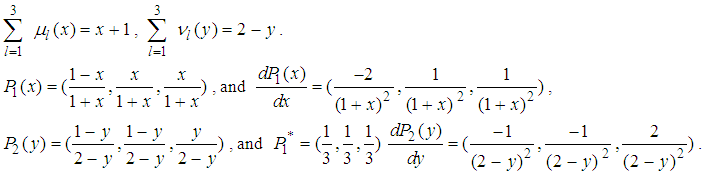One can solve the following system of linear equations.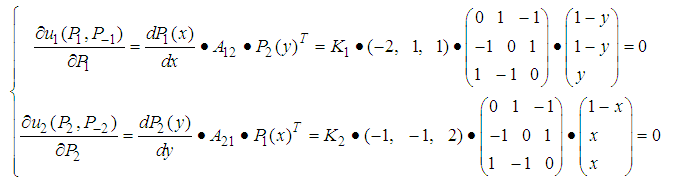

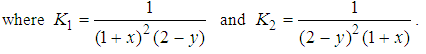The solution is 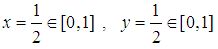. The mixed NE 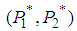with probability distributions and

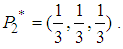Let us examine the solution 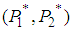for player 1 by using Hessian matrix or step 5 described in the algorithm.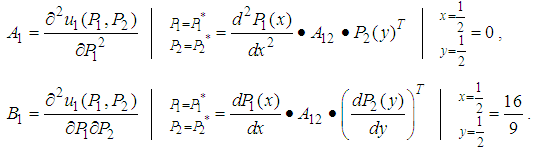

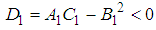. Therefore, point 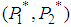is a saddle point of .

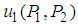Let us examine the solution 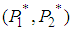for player 2.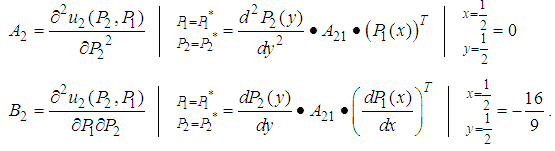

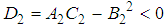. Thus, point 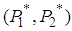is a saddle point of .

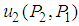Example 2 - Find mixed NE in the following 2-player game.

We define two linguistic values 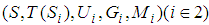, where 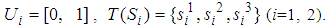The semantic rules 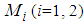are defined as follows.

,

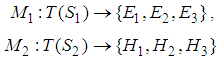where TFNs 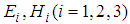are defined as follows, 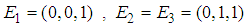; 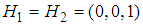, 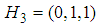. Then, we have

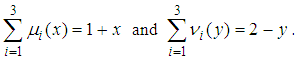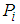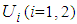The probability distribution over is as follows.

,

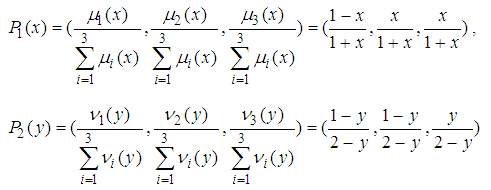Then, we have

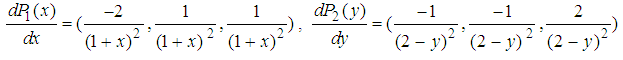One can solve the following system of linear equations.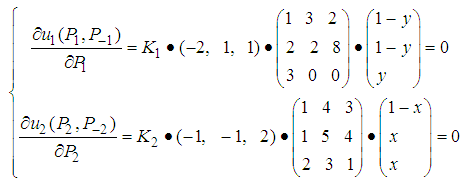

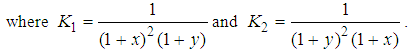The solution is 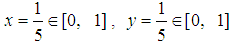. This 2-player game has a mixed NE 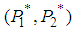with probability distribution 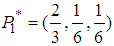and .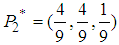

Let us examine this solution for player 1.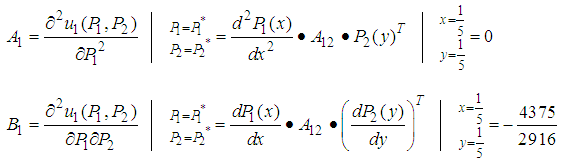

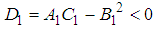. Therefore, point 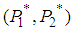is a saddle point of .

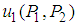Let us examine the solution for player 2.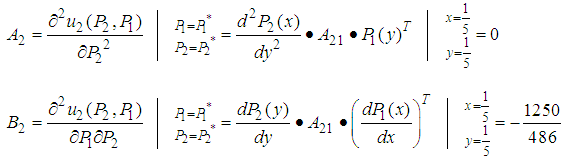

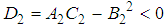. Thus, point 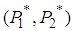is a saddle point of .

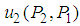Example 3 - Find mixed NE for the following bi-matrix game.

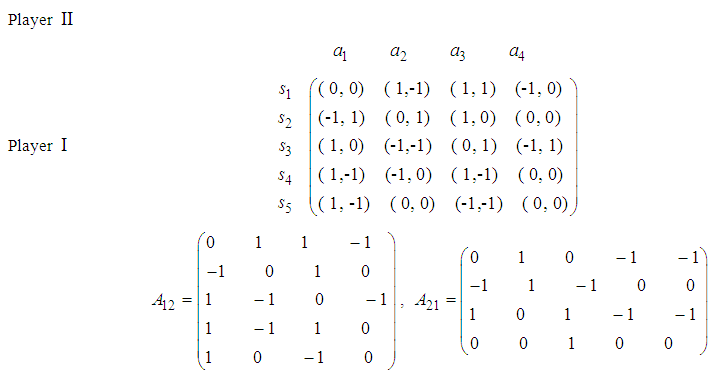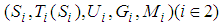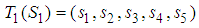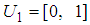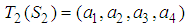We build two linguistic values . on . on 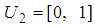, and the semantic rule 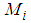is defined as follows.

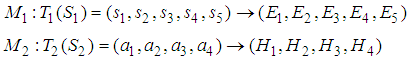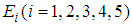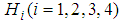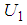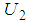where and are TFNs defined in and as follows.

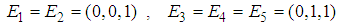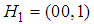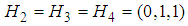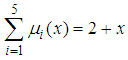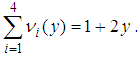and , . Then, we have and The probability distribution 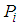over 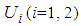is as follows.

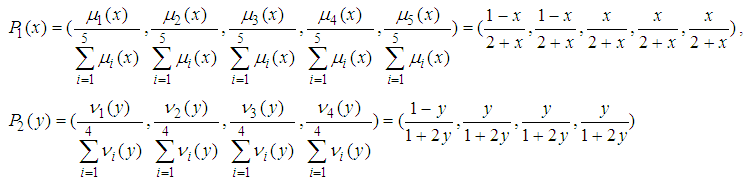Then, we have

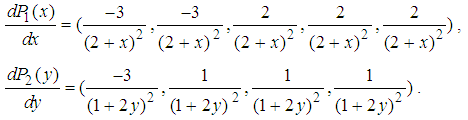One can solve the following system of linear equations.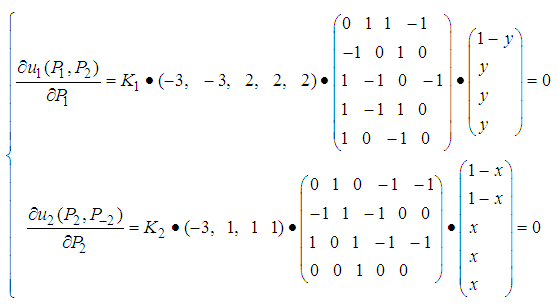

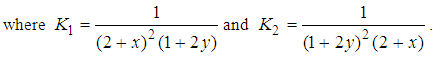The solution is 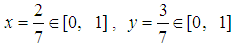. This 2-player game has a mixed NE 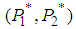with probability distribution 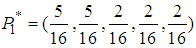and .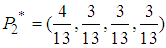

Let us examine this solution 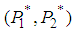for player 1.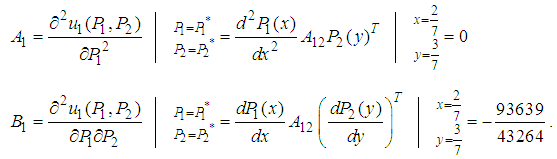

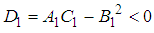. Thus, point 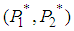is a saddle point of .

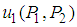Let us examine this solution 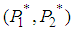for player 2.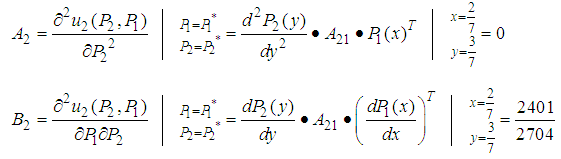

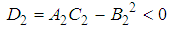. Therefore, point 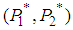is a saddle point of .

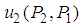5. Conclusions

This paper shows that computing mixed NE in bi-matrix games is equivalent to solving a system of linear equations. It is proved that the new algorithm can calculate mixed NE in 2-player games within polynomial time. We claim that there is a fully polynomial time scheme of calculating mixed NE in 2-player games. The algorithm can also be applied to multiplayer games if a multiplayer game is able to be reduced to a group of 2-player games.

Future study will conduct to compare the new algorithm with exiting algorithms, and to apply the new algorithm to dynamic game theory and evolutionary game theory.

ACKNOWLEDGMENTS

The author would like to thank anonymous reviewers’ comments and suggestions.