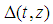Flavio Pressacco, Laura Ziani
Department of Economics and Statistics, University of Udine, Udine, Italy
Correspondence to: Laura Ziani, Department of Economics and Statistics, University of Udine, Udine, Italy.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper we intend to investigate the relationship between game theory and Fibonacci numbers. We call Fibonacci games the subset of constant sum homogeneous weighted majority games whose increasing sequence of all type weights and of the minimal winning quota is a string of consecutive Fibonacci numbers. Exploiting key properties of the Fibonacci sequence, we obtain closed form results able to provide a simple and insightful classification of such games. In detail: we show that the numerousness of Fibonacci games with t types is 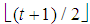 ; we describe unequivocally a Fibonacci game on the basis of its profile as a function of t and of a proper index z=1,…,
; we describe unequivocally a Fibonacci game on the basis of its profile as a function of t and of a proper index z=1,…,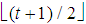 ; we provide rules concerning the behaviour of the total number n(t,z) of non-dummy players in a Fibonacci game. It turns out that there are two kinds of Fibonacci games, associated respectively with z=1 (Fibonacci-Isbell games) and z>1.
; we provide rules concerning the behaviour of the total number n(t,z) of non-dummy players in a Fibonacci game. It turns out that there are two kinds of Fibonacci games, associated respectively with z=1 (Fibonacci-Isbell games) and z>1.
Keywords:
Weighted majority games, Homogeneous representation, Minimal winning coalition, Type weight vector, Satellite games, Fibonacci numbers
Cite this paper: Flavio Pressacco, Laura Ziani, A Fibonacci Approach to Weighted Majority Games, Journal of Game Theory, Vol. 4 No. 2, 2015, pp. 36-44. doi: 10.5923/j.jgt.20150402.03.
1. Introduction
Homogeneous weighted majority games have been introduced at the origins of modern game theory by Von Neumann-Morgenstern [12] and, since then, extensively studied because of their capability to give an insightful formal framework able to analyse formation of coalitions and payoff division both in theory and in real world situations. Subsequent treatments of outstanding importance have been given by Ostmann [6], who gave the proof that any homogeneous weighted majority game (including non-constant sum ones) has a unique minimal homogeneous representation, and by Rosenmüller ([9] and [10]), who provided an analysis of the structure of such games based on the concept of characters of types and the role of satellite games.In the particular case of constant sum homogenous weighted majority games, the weights of the minimal homogeneous representation are able to capture the power of the players. Such ability is revealed by the close connections between (properly normalized) those weights and some of the outstanding ideas of “solution” of a game. Examples of such connections are: a) the stable set of imputations of the main simple solution a la Von Neumann- Morgenstern; b) the nucleolus (Peleg [7], Schmeidler [11]); c) the outcome of the Montero [5] bargaining protocol (which modifies the one proposed by Baron-Ferejohn [1]) in which both the expected payoffs and actual payoff division are proportional to the voting weights. In this paper we wish to explore the connections between constant sum homogeneous weighted majority games and Fibonacci numbers.A bridge between these two topics has been built by Isbell [2] in a vintage paper going back to the first steps of cooperative game theory. The bridge was summarized in a couple of propositions. In the first ([2], Cor. [6], p. 185), the author showed that, weakly ordering players of a n person constant sum homogeneous weighted majority game from bottom to top, the individual weight (in the minimal homogeneous representation) of the player number i could not exceed the corresponding Fibonacci number (more formally 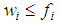 for any i=1,…,n). The second proposition ([2], third indent, p. 185) claimed that a game whose individual weights satisfied
for any i=1,…,n). The second proposition ([2], third indent, p. 185) claimed that a game whose individual weights satisfied 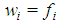 for any i=1,…,n-2,
for any i=1,…,n-2, 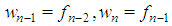 , described, for any n>2, a constant sum homogeneous weighted majority game with minimal winning quota
, described, for any n>2, a constant sum homogeneous weighted majority game with minimal winning quota  . Hence, in such games all the first n Fibonacci numbers are associated with all individual weights and the winning quota. On the basis of this connection we suggest to call Fibonacci-Isbell the set of games defined by the second proposition.Thinking in terms of type weights rather than of individual ones and keeping account that in any n person Fibonacci-Isbell game there are t=n-2 types of players, we argue that such games satisfy another slightly different "bridge" property: the bottom-top (strictly) ordered n-1 (or t+1) dimension vector of type weights and winning quota is a string of n-1 consecutive Fibonacci numbers starting from
. Hence, in such games all the first n Fibonacci numbers are associated with all individual weights and the winning quota. On the basis of this connection we suggest to call Fibonacci-Isbell the set of games defined by the second proposition.Thinking in terms of type weights rather than of individual ones and keeping account that in any n person Fibonacci-Isbell game there are t=n-2 types of players, we argue that such games satisfy another slightly different "bridge" property: the bottom-top (strictly) ordered n-1 (or t+1) dimension vector of type weights and winning quota is a string of n-1 consecutive Fibonacci numbers starting from 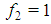 . In order to generalize this property to other feasible (n,t) combinations, we suggest to define Fibonacci games as the subset of constant sum homogeneous weighted majority games whose bottom-top increasing sequence of type weights and winning quota (in their minimal homogeneous representation) is a string of consecutive Fibonacci numbers1. Henceforth, it is convenient to use the (first order) "delayed" Fibonacci sequence g defined, for any natural n, by the relation
. In order to generalize this property to other feasible (n,t) combinations, we suggest to define Fibonacci games as the subset of constant sum homogeneous weighted majority games whose bottom-top increasing sequence of type weights and winning quota (in their minimal homogeneous representation) is a string of consecutive Fibonacci numbers1. Henceforth, it is convenient to use the (first order) "delayed" Fibonacci sequence g defined, for any natural n, by the relation 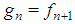 , and delayed Fibonacci subsequences
, and delayed Fibonacci subsequences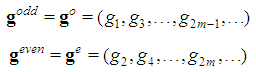 Moreover, following Rosenmüller ([10], p. 311), we take into consideration the "profile" of a constant sum homogeneous weighted majority game with t types denoted by the ordered vector
Moreover, following Rosenmüller ([10], p. 311), we take into consideration the "profile" of a constant sum homogeneous weighted majority game with t types denoted by the ordered vector 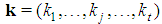 , whose component
, whose component 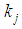 is the number of players of type j in the game.After that, it becomes clear that Fibonacci games are unequivocally described by feasible triplets
is the number of players of type j in the game.After that, it becomes clear that Fibonacci games are unequivocally described by feasible triplets 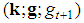 in which the profile k and the delayed Fibonacci sequence g share the dimension t, gj is the weight of players of type j, gt+1 is the winning quota and a triplet is feasible if it meets the homogeneity conditions (see [7], Theor. 3.5 and the “test” of homogeneity2 [9], Theor.1.4).In our paper, we give a simple but insightful characterization of the feasible profiles k of Fibonacci games with t types. The proof of such a characterization largely exploits fundamental properties of the delayed Fibonacci sequence (as for the necessary conditions) and the satellite game approach (in the sufficiency part).As a consequence, for any positive integer t, there are altogether3
in which the profile k and the delayed Fibonacci sequence g share the dimension t, gj is the weight of players of type j, gt+1 is the winning quota and a triplet is feasible if it meets the homogeneity conditions (see [7], Theor. 3.5 and the “test” of homogeneity2 [9], Theor.1.4).In our paper, we give a simple but insightful characterization of the feasible profiles k of Fibonacci games with t types. The proof of such a characterization largely exploits fundamental properties of the delayed Fibonacci sequence (as for the necessary conditions) and the satellite game approach (in the sufficiency part).As a consequence, for any positive integer t, there are altogether3 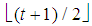 Fibonacci games, i.e. the Fibonacci-Isbell one and other
Fibonacci games, i.e. the Fibonacci-Isbell one and other 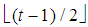 games. Moreover, it turns out that any two Fibonacci games with the same t have a different number n of non-dummy players. Hence, it seems logical to associate, for any t, the Fibonacci games with the set of integers
games. Moreover, it turns out that any two Fibonacci games with the same t have a different number n of non-dummy players. Hence, it seems logical to associate, for any t, the Fibonacci games with the set of integers 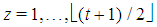 in such a way that the number n(t,z) of players (in the Fibonacci game with t types and index z) is an increasing function of z.A closed form description of the behavior of the function n(t,z) is also provided. It is surprising to verify that the derived function
in such a way that the number n(t,z) of players (in the Fibonacci game with t types and index z) is an increasing function of z.A closed form description of the behavior of the function n(t,z) is also provided. It is surprising to verify that the derived function 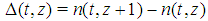 is resumed by a matrix whose columns are the entire delayed Fibonacci sequence (whose starting point is properly shifted down with z), while the rows are, in backward order, the delayed Fibonacci subsequences coherent with the parity of t (properly truncated, so as the row t has
is resumed by a matrix whose columns are the entire delayed Fibonacci sequence (whose starting point is properly shifted down with z), while the rows are, in backward order, the delayed Fibonacci subsequences coherent with the parity of t (properly truncated, so as the row t has 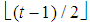 components).We are well aware of the existence of a vast body of literature concerning applications of homogeneous weighted majority games (constant as well as non-constant sum) to the analysis of voting power and committees interactions. Besides already cited papers, other examples may be found e.g. in Kalandrakis [3], Le Breton et al [4]. Yet we do not discuss applications of the Fibonacci games here in this or in other fields. Anyway, we anticipate that we have some preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.Yet we do not discuss applications of the Fibonacci games here in this or in other fields, but we anticipate that we have some (not yet published) preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.The plan of the paper is as follows: section 2 gives a short description of the basic notations used in the paper and recalls well known concepts of homogeneous weighted majority games; section 3 defines Fibonacci games and resumes the main results of the paper; section 4 provides an explicit description of the profiles of Fibonacci games for some small values of t; the behaviour of the n(t,z) and of
components).We are well aware of the existence of a vast body of literature concerning applications of homogeneous weighted majority games (constant as well as non-constant sum) to the analysis of voting power and committees interactions. Besides already cited papers, other examples may be found e.g. in Kalandrakis [3], Le Breton et al [4]. Yet we do not discuss applications of the Fibonacci games here in this or in other fields. Anyway, we anticipate that we have some preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.Yet we do not discuss applications of the Fibonacci games here in this or in other fields, but we anticipate that we have some (not yet published) preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.The plan of the paper is as follows: section 2 gives a short description of the basic notations used in the paper and recalls well known concepts of homogeneous weighted majority games; section 3 defines Fibonacci games and resumes the main results of the paper; section 4 provides an explicit description of the profiles of Fibonacci games for some small values of t; the behaviour of the n(t,z) and of 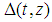 functions and their connections with the delayed Fibonacci (sub)sequences are presented and discussed in section 5; all the proofs are grouped in sections 6 and 7; conclusions follow in the final section 8.
functions and their connections with the delayed Fibonacci (sub)sequences are presented and discussed in section 5; all the proofs are grouped in sections 6 and 7; conclusions follow in the final section 8.
2. Notations
Let 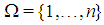 denote the set of non-dummy players of a simple constant sum game in characteristic function form. A simple game is a mapping
denote the set of non-dummy players of a simple constant sum game in characteristic function form. A simple game is a mapping 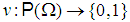 such that
such that 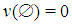 and
and 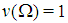 , and a coalition
, and a coalition 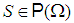 is winning if its payoff
is winning if its payoff 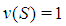 and losing otherwise. A simple game is constant sum if
and losing otherwise. A simple game is constant sum if 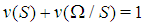 for any S. Moreover, S is minimal winning if, for any player
for any S. Moreover, S is minimal winning if, for any player 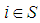 ,
, 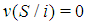 .A simple weighted majority game is described by the pair
.A simple weighted majority game is described by the pair 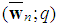 where4
where4 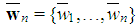 is the (weakly) ordered vector (
is the (weakly) ordered vector (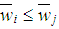 for i) of individual weights and q the winning quota of the game. Thus the weight of S is
for i) of individual weights and q the winning quota of the game. Thus the weight of S is 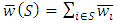 and
and 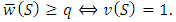 A simple constant sum homogeneous weighted majority game is described by its minimal homogeneous representation, that is the ordered vector
A simple constant sum homogeneous weighted majority game is described by its minimal homogeneous representation, that is the ordered vector 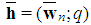 which meets the homogeneity conditions, that is
which meets the homogeneity conditions, that is 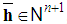 ,
, 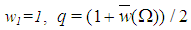 and
and 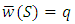 for any minimal winning coalition.The vector
for any minimal winning coalition.The vector 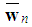 of the minimal homogeneous representation induces a decomposition of
of the minimal homogeneous representation induces a decomposition of 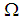 in equivalence classes K1,…,Kj,…,Kt.. Each class groups all players of the same type, sharing the same individual weight and the corresponding (strongly) ordered type weight vector is:
in equivalence classes K1,…,Kj,…,Kt.. Each class groups all players of the same type, sharing the same individual weight and the corresponding (strongly) ordered type weight vector is: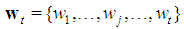 with
with 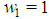 .Coherently,
.Coherently, 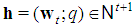 , but to unequivocally describe a game it is necessary also to introduce also the profile
, but to unequivocally describe a game it is necessary also to introduce also the profile 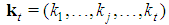 with
with 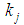 the number of players of type j in the game. Thus, a constant sum homogeneous weighted majority game is described by
the number of players of type j in the game. Thus, a constant sum homogeneous weighted majority game is described by 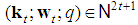 .Finally, we denote by
.Finally, we denote by 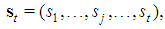 with
with 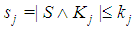 , the "profile" of the coalition S, so that
, the "profile" of the coalition S, so that 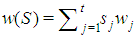 is an alternative formalization of the weight of S and, by homogeneity,
is an alternative formalization of the weight of S and, by homogeneity, 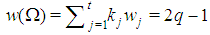 .
.
3. Fibonacci Games: Main Results
The Fibonacci sequence f is defined by the well known finite difference equation: 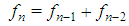 holding for any natural n>2 with initial conditions
holding for any natural n>2 with initial conditions 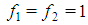 . Henceforth, we exploit the "delayed" Fibonacci sequence
. Henceforth, we exploit the "delayed" Fibonacci sequence 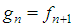 for any n, and denote, for any integer m, by
for any n, and denote, for any integer m, by 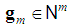 the vector
the vector 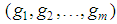 . Coherently, the denumerable sequence
. Coherently, the denumerable sequence 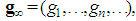 and
and 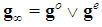 with
with 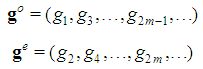 the two denumerable (sub)sequences obtained extracting from
the two denumerable (sub)sequences obtained extracting from 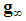 all elements of odd or, respectively, even index.Definition 3.1 The set of Fibonacci games is the subset of constant sum homogeneous weighted majority games with
all elements of odd or, respectively, even index.Definition 3.1 The set of Fibonacci games is the subset of constant sum homogeneous weighted majority games with 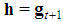 , that is
, that is 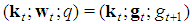 . Remark 3.1 Feasibility conditions require that in any Fibonacci game with t types,
. Remark 3.1 Feasibility conditions require that in any Fibonacci game with t types,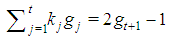 constant for any kt: the winning quota is the same for all Fibonacci games with the same t. Proof. Homogeneity requires that
constant for any kt: the winning quota is the same for all Fibonacci games with the same t. Proof. Homogeneity requires that 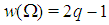 , i.e.
, i.e.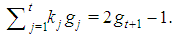
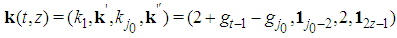 | (1) |
or, putting 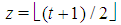 in order to have a complete indexation of the games, by:
in order to have a complete indexation of the games, by: 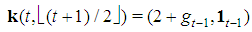 | (2) |
Corollary 3.1 For any t, there are exactly 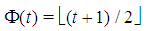 | (3) |
Fibonacci games with t types. Let us denote by n(t,z) the total number of non-dummy players in a Fibonacci game with t types and index z. Theorem 3.2 For any t, 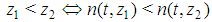 . Proofs of Th. 3.1 and 3.2 follow in sections 6 and 7.
. Proofs of Th. 3.1 and 3.2 follow in sections 6 and 7.
4. Profile of Fibonacci Games
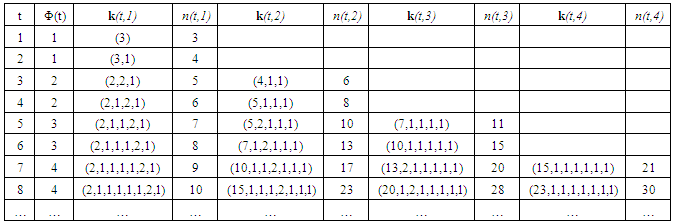
According to the Definition 3.1, given t there are no degrees of freedom in the choice of the sequence of type weights and of the winning quota. Hence, a Fibonacci game is unequivocally described by its k(t,z) vector that follows the rules described in Formulas (1) and (2). Table 1 helps to understand the structure of the profile vectors of Fibonacci games for a set of small values of t. We distinguish between two patterns of profiles: for 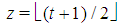 (the last vector of each row), all type components, except the bottom one, are 1, while this latter component plays a balancing role (according to Formula (2)); for all the other z, there is just one (non bottom) component equal to 2 in place
(the last vector of each row), all type components, except the bottom one, are 1, while this latter component plays a balancing role (according to Formula (2)); for all the other z, there is just one (non bottom) component equal to 2 in place 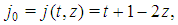 all the others (non bottom) are still 1 and, again, the bottom component plays the balancing role (according to Formula (1)).
all the others (non bottom) are still 1 and, again, the bottom component plays the balancing role (according to Formula (1)).Table 1. The profile k(t,z) for a set of small values of t
 |
| |
|
5. The Behavior of n(t,z)
In this section we investigate the relation between the number of non-dummy players in the game and the characterization of the Fibonacci games by means of the profile vectors. In particular, the following properties give an answer to the questions: “given n, how many Fibonacci games are there?” and “which kind of Fibonacci games do we find?”The properties, which hold for any feasible combination of (t,z), are the following:Property 5.1 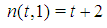 | (4) |
Property 5.2 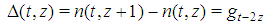 | (5) |
Property 5.3 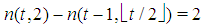 | (6) |
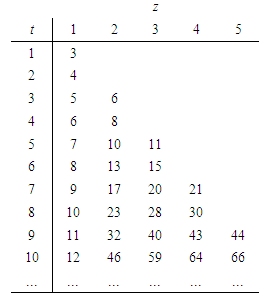
Proofs of these Properties are given in the section 7.In Table 2 we show the behavior of the function n(t,z).Table 2. List of values n(t,z)
 |
| |
|
As it may be observed, there is not one to one correspondence between the number n of players and each feasible combination of (t,z). Essentially, for any value of n>2, there are surely at least one Fibonacci game or, at most, two of them. As a consequence, we distinguish between two kinds of Fibonacci games: the first one corresponds to z=1 and Formula (4) implies that there is exactly one Fibonacci game (of this kind) for any n>2. We recall that such Fibonacci-Isbell games have been described by Isbell ([2], p. 185) while studying the class of coalitionally Parsimonious games5. The second one emerges for z>1: precisely, there is only one Fibonacci game (of this second kind) for sparse values of n.Summing up, there are values of n corresponding to two Fibonacci games (one of the first and one of the second kind), while for other values of n there is just one Fibonacci game of the first kind. For example, for n = 8, there are one Fibonacci game of the first kind (z=1, t=6), and one of the second kind (z=2, t=4);while for n =9, there is just one Fibonacci game of the first kind (z=1, t=7).At first glance the values of n associated with the second kind of games seem to follow a chaotic rule. Indeed, a regularity emerges once we consider the following table of the differences generated by Property 5.2 (see also Remark 7.1).Table 3. Table of the function
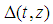
 |
| |
|
Note that the rows corresponding to odd (even) values of t are backward initial strings with 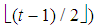 elements of the Fibonacci subsequence
elements of the Fibonacci subsequence 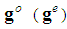 . In turn, the columns are nothing but the whole Fibonacci sequence
. In turn, the columns are nothing but the whole Fibonacci sequence 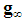 whose starting point is shifted at the row t=1+2z.
whose starting point is shifted at the row t=1+2z.
6. Proofs of Theorem 3.1
Proof. For t=1: 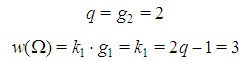 Hence there are three players with weight
Hence there are three players with weight  ,
, 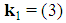 and
and 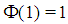 . For t=2:
. For t=2: 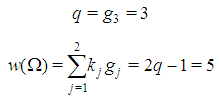 Hence,
Hence, 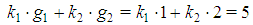 . There are two solutions
. There are two solutions 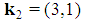 and
and 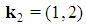 but the second is not feasible because the profile
but the second is not feasible because the profile 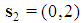 identifies a minimal winning coalition S with w(S)=4>q, incompatible with the homogeneous character. On the other side, the first solution is feasible with profiles (3,0) and (1,1) of the minimal winning coalitions, so that
identifies a minimal winning coalition S with w(S)=4>q, incompatible with the homogeneous character. On the other side, the first solution is feasible with profiles (3,0) and (1,1) of the minimal winning coalitions, so that 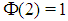 . For t>2, we show at first that the conditions (1) or (2) are necessary for Fibonacci games and then that they are also sufficient.
. For t>2, we show at first that the conditions (1) or (2) are necessary for Fibonacci games and then that they are also sufficient.
6.1. Proof of Necessity
Property 6.1 In any Fibonacci game with t>1, the coalition S whose profile st=(0t-2,12), i.e. made by a top and a last but top player, is minimal winning. Proof. 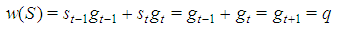 Property 6.2 In any Fibonacci game with t>1, kt=1. Proof. Otherwise the coalition S:st=(0t-1,2) would be minimal winning with
Property 6.2 In any Fibonacci game with t>1, kt=1. Proof. Otherwise the coalition S:st=(0t-1,2) would be minimal winning with 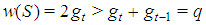 , a contradiction with the homogeneous character of the game. Property 6.3 In any Fibonacci game with t>2,
, a contradiction with the homogeneous character of the game. Property 6.3 In any Fibonacci game with t>2, 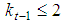 . Proof. Otherwise the coalition S:st=(0t-2,3,0) would be minimal winning as
. Proof. Otherwise the coalition S:st=(0t-2,3,0) would be minimal winning as 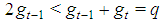 with
with 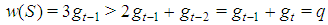 . Property 6.4 In any Fibonacci game with t>3, kt-2=1. Proof. Suppose on the contrary, kt-2>1and consider the coalition S:st=(0t-3,2,0,1). S would be minimal winning too as gt+gt-2t+gt-1=q with w(S)=gt+2gt-2>gt+gt-2+gt-3=gt +gt-1=q. A contradiction. Properties 6.3 and 6.4 may be generalized to types (t-h) with h odd and respectively h even.Property 6.5 In any Fibonacci game it is
. Property 6.4 In any Fibonacci game with t>3, kt-2=1. Proof. Suppose on the contrary, kt-2>1and consider the coalition S:st=(0t-3,2,0,1). S would be minimal winning too as gt+gt-2t+gt-1=q with w(S)=gt+2gt-2>gt+gt-2+gt-3=gt +gt-1=q. A contradiction. Properties 6.3 and 6.4 may be generalized to types (t-h) with h odd and respectively h even.Property 6.5 In any Fibonacci game it is 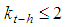 for h odd Proof. Proof of Property 6.5 is based on the following lemma: Lemma 6.1 In a Fibonacci game consider any player of type j0=(t-h) with h odd <(t-1); there exists a minimal winning coalition S in which this player is the weakest. The profile of S is given by:
for h odd Proof. Proof of Property 6.5 is based on the following lemma: Lemma 6.1 In a Fibonacci game consider any player of type j0=(t-h) with h odd <(t-1); there exists a minimal winning coalition S in which this player is the weakest. The profile of S is given by: 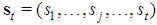 with
with 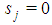 for j0;
for j0; 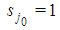 ;
; 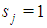 for j>j0 and
for j>j0 and 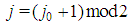 and
and 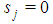 for j>j0 and
for j>j0 and 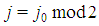 .Proof.
.Proof. 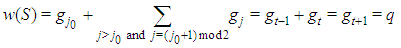 Now to prove Property 6.5 suppose on the contrary
Now to prove Property 6.5 suppose on the contrary 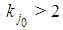 and consider the coalition
and consider the coalition 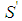 obtained from S by replacement of the player type
obtained from S by replacement of the player type 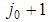 with two additional players of type
with two additional players of type 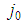 .
. 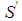 would be minimal winning with
would be minimal winning with 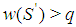 , a contradiction.Property 6.6 In any Fibonacci game it is
, a contradiction.Property 6.6 In any Fibonacci game it is 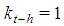 for h even Proof. Proof of Property 6.6 is based on the previous Lemma 6.1 and on the following one:Lemma 6.2 Suppose in a Fibonacci game there is a minimal winning coalition S and a
for h even Proof. Proof of Property 6.6 is based on the previous Lemma 6.1 and on the following one:Lemma 6.2 Suppose in a Fibonacci game there is a minimal winning coalition S and a 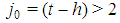 such that
such that 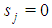 for
for 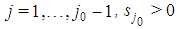 (so that a player of type
(so that a player of type 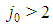 is the weakest in S), then kj0-1=1. Proof. Suppose on the contrary kj0-1>1 and consider the coalition
is the weakest in S), then kj0-1=1. Proof. Suppose on the contrary kj0-1>1 and consider the coalition 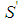 obtained from S by replacement of a player of type
obtained from S by replacement of a player of type 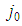 with two players of type
with two players of type 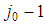 .
. 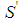 would be minimal winning with
would be minimal winning with 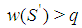 , a contradiction. This Lemma holds independently from the parity of h. Lemma 6.3 If a player of type j=t-h>2 is the weakest in a minimal winning coalition S, then there exists a minimal winning coalition
, a contradiction. This Lemma holds independently from the parity of h. Lemma 6.3 If a player of type j=t-h>2 is the weakest in a minimal winning coalition S, then there exists a minimal winning coalition 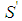 such that a player of type j-2 is the weakest in
such that a player of type j-2 is the weakest in 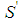 .Proof. In S replace the player of type j with the unique (by Lemma 6.2) player of type j-1 and one player of type j-2. Also this Lemma holds independently from the parity of h. Lemma 6.4 Suppose in a Fibonacci game
.Proof. In S replace the player of type j with the unique (by Lemma 6.2) player of type j-1 and one player of type j-2. Also this Lemma holds independently from the parity of h. Lemma 6.4 Suppose in a Fibonacci game 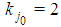 for j0=t-h with h odd <(t-1), then: a)
for j0=t-h with h odd <(t-1), then: a) 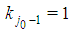 (by Property 6.6) and b) there is a minimal winning coalition
(by Property 6.6) and b) there is a minimal winning coalition 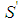 such that the player of type
such that the player of type 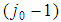 is its weakest player. Proof. (of part b))
is its weakest player. Proof. (of part b)) 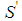 is obtained from the coalition S in Lemma 6.1 by replacement of the player of type t-(h-1) with one additional player of type t-h and the player of type t-(h+1). Clearly
is obtained from the coalition S in Lemma 6.1 by replacement of the player of type t-(h-1) with one additional player of type t-h and the player of type t-(h+1). Clearly 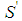 is minimal winning with
is minimal winning with 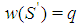 . Lemma 6.5 If in a Fibonacci game
. Lemma 6.5 If in a Fibonacci game 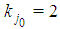 for j0=t-h with h odd <(t-1), then
for j0=t-h with h odd <(t-1), then 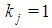 for any
for any 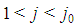 . Proof. Lemma 6.4 and Lemma 6.3 imply that there exists a set of minimal winning coalitions such that each player of type j,
. Proof. Lemma 6.4 and Lemma 6.3 imply that there exists a set of minimal winning coalitions such that each player of type j, 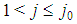 , is the weakest in a minimal winning coalition of the set. After that Lemma 6.5 comes as an immediate corollary of Lemma 6.2. Now, it is possible to give a more precise statement of Property 6.5 concerning the behaviour of
, is the weakest in a minimal winning coalition of the set. After that Lemma 6.5 comes as an immediate corollary of Lemma 6.2. Now, it is possible to give a more precise statement of Property 6.5 concerning the behaviour of 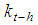 for h odd <(t-1). Indeed, Property 6.5 and Lemma 6.5 give immediately:Property 6.7 In a Fibonacci game there is at most one odd h<(t-1) such that
for h odd <(t-1). Indeed, Property 6.5 and Lemma 6.5 give immediately:Property 6.7 In a Fibonacci game there is at most one odd h<(t-1) such that 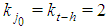 and
and 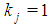 for all j>1 and
for all j>1 and 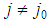 . Now by Remark 3.1 it is:
. Now by Remark 3.1 it is: 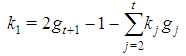 | (7) |
and moreover6: 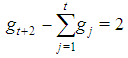 | (8) |
Furthermore, Properties 6.6 and 6.7 imply that, for any 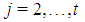 , kt satisfies conditions (1) or (2). In the first case and putting
, kt satisfies conditions (1) or (2). In the first case and putting 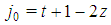 , we obtain:
, we obtain: 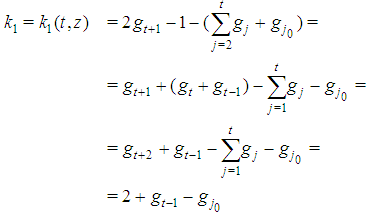 | (9) |
In particular, for z=1, 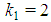 .In the second case, we get immediately:
.In the second case, we get immediately: 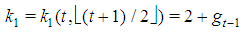 | (10) |
To resume, by Properties 6.6 and 6.7, and by Formulas (9) and (10), necessary conditions to be satisfied by the kt vector of a Fibonacci game with t>2 are those described in Formulas (1) and (2).
6.2. Proof of Sufficiency
The proof is based on an adaptation to our problem of the test for homogeneity of a weighted majority game developed as Basic Lemma in [9] (Theorem 1.4) and [10] (pp. 312).Henceforth we use the following definitions and notations: • 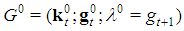 , "seed" game with
, "seed" game with 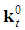 given by Formulas (1) or (2). In particular,
given by Formulas (1) or (2). In particular, 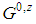 , seed game as a function of
, seed game as a function of 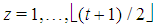 .•
.• 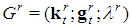 , any game of a r generation7 derived by the seed
, any game of a r generation7 derived by the seed 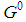 . Note that the dimension t of
. Note that the dimension t of 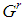 depends on r. Whenever useful, we utilize t(r). In particular,
depends on r. Whenever useful, we utilize t(r). In particular, 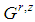 , game of a
, game of a 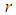 generation derived by the seed
generation derived by the seed 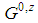 .• Feasible (not feasible) game: a
.• Feasible (not feasible) game: a 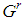 for which
for which 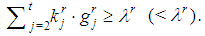 • For any given type index
• For any given type index 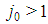 , an "intermediate" player in the game
, an "intermediate" player in the game 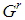 is a player of type
is a player of type 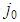 , a "large" player is a player of any type
, a "large" player is a player of any type 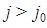 , a "small" player is any player of type
, a "small" player is any player of type 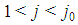 .• No bottom coalition of a feasible game
.• No bottom coalition of a feasible game 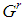 : a coalition
: a coalition 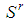 whose profile
whose profile 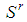 has
has 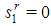 .• Dominant coalition8 of a feasible game
.• Dominant coalition8 of a feasible game 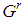 a coalition
a coalition 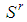 such that:(a)
such that:(a) 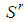 is no bottom(b) there is an index
is no bottom(b) there is an index 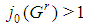 (or shortly
(or shortly 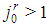 ) and a positive integer
) and a positive integer 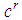 , such that
, such that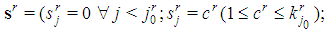
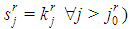 i.e.
i.e. 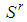 is made by all large players and by some (may be all) intermediate players, so that
is made by all large players and by some (may be all) intermediate players, so that 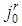 is the type index corresponding to the weakest player in the dominant coalition
is the type index corresponding to the weakest player in the dominant coalition 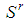 .(c)
.(c) 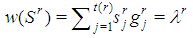 • Generation rules. Let
• Generation rules. Let 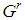 a feasible game,
a feasible game, 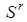 its dominant coalition and
its dominant coalition and 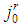 the corresponding type index. To any
the corresponding type index. To any 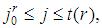 associate the game
associate the game 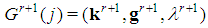 in which
in which 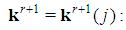 - for
- for 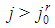 and
and 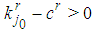 :
: 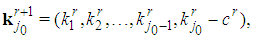 the dimension of
the dimension of 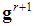 is j0 and
is j0 and 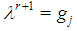 - for
- for 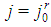 or
or 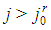 and
and 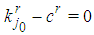 :
: 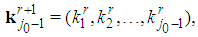 the dimension of
the dimension of 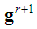 is
is 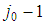 and
and 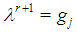 Verbally the dominant coalition
Verbally the dominant coalition 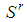 generates as many "satellite" games
generates as many "satellite" games 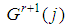 as the number of types j included in the coalition. The players of the satellite game associated with a type j are all players of type i not belonging to
as the number of types j included in the coalition. The players of the satellite game associated with a type j are all players of type i not belonging to 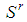 ; the winning quota is gj. The idea is that any satellite game looks for the dominant coalition of the satellite able to replace one player of type j in the generating game, while preserving the homogeneous character of the "seed" game. In turn, the dominant coalition gives rise to other satellite games of next generation and so on.Now, our adapted version of Basic Lemma is: Lemma 6.6 A seed weighted majority game
; the winning quota is gj. The idea is that any satellite game looks for the dominant coalition of the satellite able to replace one player of type j in the generating game, while preserving the homogeneous character of the "seed" game. In turn, the dominant coalition gives rise to other satellite games of next generation and so on.Now, our adapted version of Basic Lemma is: Lemma 6.6 A seed weighted majority game 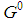 is homogeneous if, in the set of all
is homogeneous if, in the set of all 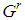 games obtained by the generation rules, do not exist feasible games lacking the dominant coalition. To prove the Lemma 6.6 we show that any game of the set
games obtained by the generation rules, do not exist feasible games lacking the dominant coalition. To prove the Lemma 6.6 we show that any game of the set 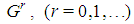 generated by a seed
generated by a seed 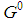 coherent with formulae (1) and (2) either is not feasible or admits a dominant coalition.
coherent with formulae (1) and (2) either is not feasible or admits a dominant coalition.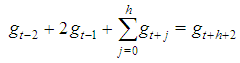 | (11) |
Proof. Let us distinguish three cases:Case 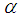 ):
): 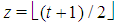 Let us denote
Let us denote 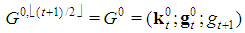 any seed game with
any seed game with 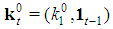 . The profile of the dominant coalition
. The profile of the dominant coalition 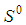 is
is 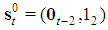 with
with 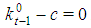 . Hence the satellite games associated with type t-1 and t are
. Hence the satellite games associated with type t-1 and t are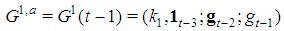 and
and 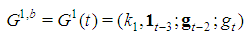 By Formula (8),
By Formula (8), 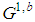 is not feasible, while
is not feasible, while 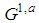 is feasible for any
is feasible for any 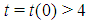 . Let us write briefly
. Let us write briefly 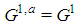 ; it is immediate to check that
; it is immediate to check that 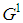 mimics the structure of
mimics the structure of 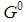 : only the dimension is different: it is
: only the dimension is different: it is 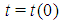 for
for 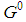 and
and 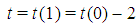 for
for 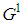 . The profile of the dominant coalition
. The profile of the dominant coalition 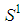 of
of 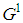 is
is 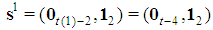 and the procedure may be recursively repeated until the integer r for which also
and the procedure may be recursively repeated until the integer r for which also 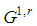 is no longer feasible. This is resumed by the following.Property 6.8 Let
is no longer feasible. This is resumed by the following.Property 6.8 Let 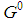 be a seed game of type
be a seed game of type 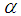 with t=t(0)>2. For any generation
with t=t(0)>2. For any generation 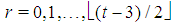 there is a unique feasible
there is a unique feasible 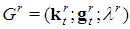 . The
. The 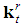 of such game is
of such game is 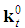 truncated at dimension tr=t(0)-2r, which is coherently the dimension of
truncated at dimension tr=t(0)-2r, which is coherently the dimension of 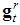 , while
, while 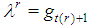 . Feasible
. Feasible 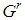 games have dominant coalition
games have dominant coalition 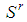 whose
whose 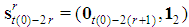 .
. 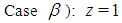 Let
Let 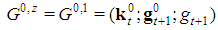 any seed game with
any seed game with 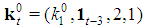 . The profile of the dominant coalition
. The profile of the dominant coalition 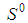 is still
is still 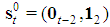 with
with 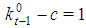 . Hence, the satellite games associated to type t-1 and t are
. Hence, the satellite games associated to type t-1 and t are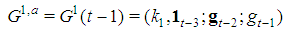 and
and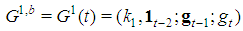 Both games share the properties of
Both games share the properties of 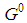 of case
of case 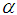 ), that is behave as seed games and generate for r=2,… sequences
), that is behave as seed games and generate for r=2,… sequences 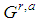 and
and 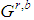 according to Property 6.8. Of course the dimension of
according to Property 6.8. Of course the dimension of 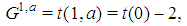 and of
and of 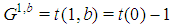 .
.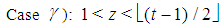 Let us write
Let us write 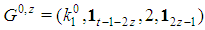 . The profile of the dominant coalition
. The profile of the dominant coalition 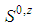 is
is 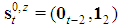 with
with 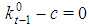 . Let us denote the two satellite games by
. Let us denote the two satellite games by 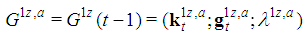 and
and 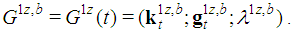 It is
It is 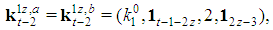
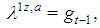 and
and 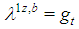 . Note that
. Note that 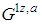 mimics
mimics 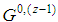 ; hence recursively we go back to
; hence recursively we go back to 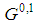 , i.e. the seed game of case
, i.e. the seed game of case 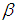 ).In turn, as by Formula (11),
).In turn, as by Formula (11), 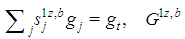 has dominant coalition with profile.
has dominant coalition with profile. 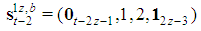 Hence
Hence 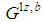 gives rise to 2z-1 satellite games
gives rise to 2z-1 satellite games 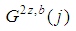 for
for 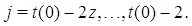 It is
It is 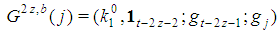 . By Formula (8), for all j, except
. By Formula (8), for all j, except 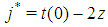 , the
, the 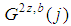 are not feasible; the survival feasible
are not feasible; the survival feasible 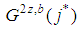 mimics the behavior of the
mimics the behavior of the 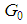 seed of the case
seed of the case 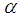 ).Summing up, in all three cases all
).Summing up, in all three cases all 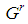 games either are not feasible, or if feasible admit a dominant coalition and the conditions of the Basic Lemma are verified.
games either are not feasible, or if feasible admit a dominant coalition and the conditions of the Basic Lemma are verified.
7. Proofs of Properties of Section 5
By definition: 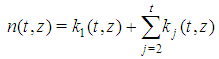 | (12) |
Proof. Proof of Property 5.1.For 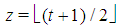 it is
it is 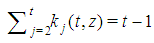 , by Formula (2) and
, by Formula (2) and 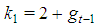 by Formula (10) so that:
by Formula (10) so that: 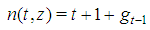 | (13) |
For 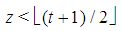 it is
it is 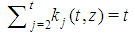 , by Formula (1) and
, by Formula (1) and 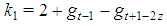 by Formula (9) so that:
by Formula (9) so that: 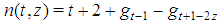 | (14) |
and in particular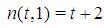 Proof. Proof of Property 5.2.For
Proof. Proof of Property 5.2.For 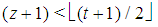 by Formula (14):
by Formula (14): 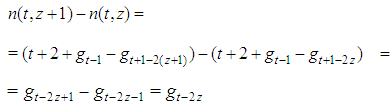 | (15) |
For 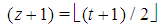 by Formulas (13) and (14):
by Formulas (13) and (14): 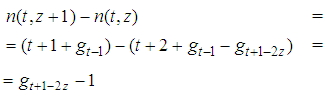 | (16) |
but 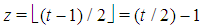 for t even and
for t even and 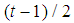 for t odd so that: t+1-2z=3 for t even and t+1-2z=2 for t oddwhich also means, on one side: t-2z=2 for t even and t-2z=1 for t odd
for t odd so that: t+1-2z=3 for t even and t+1-2z=2 for t oddwhich also means, on one side: t-2z=2 for t even and t-2z=1 for t odd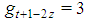 for t even and
for t even and 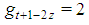 for t oddand finally
for t oddand finally 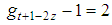 for t even and
for t even and 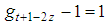 for t oddso that in both cases still
for t oddso that in both cases still 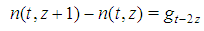 | (17) |
which completes the proof of Property 5.2. Note that this property implies the strict monotony of 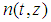 for any t and then, as a by product, gives a proof of Theorem 3.2. Proof. Proof of Property 5.3.Preliminarily note that putting
for any t and then, as a by product, gives a proof of Theorem 3.2. Proof. Proof of Property 5.3.Preliminarily note that putting 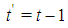 it is
it is 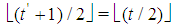 so that by Formula (13):
so that by Formula (13):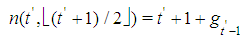 | (18) |
equivalent to 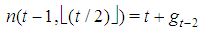 Moreover, it is by Formula (14) for t>4, or by Formula (13) for t=3 and 410
Moreover, it is by Formula (14) for t>4, or by Formula (13) for t=3 and 410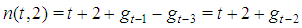 and immediately:
and immediately: 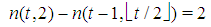 | (19) |
Remark 7.1 Jointly Prop. 5.2 and 5.3 imply that, putting in lexicographic order the set 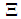 of values of n(t,z), z>1, a strictly monotone sequence is obtained. By Formulas (15), (17) and (19), all members of the sequence of first differences
of values of n(t,z), z>1, a strictly monotone sequence is obtained. By Formulas (15), (17) and (19), all members of the sequence of first differences  of the
of the 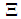 sequence are Fibonacci numbers (see Table 3).
sequence are Fibonacci numbers (see Table 3).
8. Conclusions
In this paper we introduce the class of Fibonacci games. They are the subset of constant sum homogeneous weighted majority games whose sequence of all type weights and the minimal winning quota is a string of consecutive Fibonacci numbers. Exploiting properties of the Fibonacci sequence, we give closed form results able to provide a simple and insightful characterization of such games. In more detail, we compute the total number of Fibonacci games for any given value of t (type of players in the game); we describe, for any (t,z) with z a proper counter, the profile of any game, i.e. the vector whose components are the number of non dummy players of each type in the game; we provide a recursive rule to compute the function n(t,z) which gives the overall number of non dummy players in the (t,z) game and we underline that such rule may be summarized through a matrix whose columns and rows are exactly sequences (or subsequences for rows) of Fibonacci numbers. Compared to other weighted majority games, the Fibonacci games combine two specific characteristics: the presence of some, or perhaps many, "peones" (players with minimum weight), along with an almost total ranking (with one tie at most) of all the other players, whose individual power grows at the speed of the Fibonacci sequence. It seems, by some preliminary analysis, that this feature might be useful in applications to weighted voting systems in parliamentary elections. In particular, it might be worthwhile investigating the consequences coming from the assignment of a wide proposal power besides the voting rights to the strongest player. This would be the object of further research.
Notes
1. Of course other definitions, based on more or less restrictive conditions on Fibonacci numbers, could have been chosen. An alternative approach on this line has been proposed by Gambarelli, Gnocchi and Pressacco in an unpublished communication presented in the section "Power indices" at the conference: Models of collusion, games and decisions for applications to judging, selling and voting. Oldofredi Castle, Monte Isola 18-19 June 2012.2. Roughly speaking, the test of homogeneity requires that, given a candidate homogeneous representation of a game, the measure of the largest (when collecting players according to rank) minimal winning coalition must exactly hit the winning quota and that each player i of this coalition induces (recursively) a (satellite) game whose winning quota is given by her weight 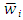 and either is exactly hit by the largest minimal winning coalition obtained by remaining players of smaller weight or the global weight of all these players is lower than
and either is exactly hit by the largest minimal winning coalition obtained by remaining players of smaller weight or the global weight of all these players is lower than 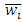 .3. As usual
.3. As usual 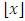 denotes the floor (x). In particular, for t integer even (odd),
denotes the floor (x). In particular, for t integer even (odd), 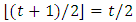 (or (t+1)/2)).4. Henceforth the subscript of the vector is its dimension, not to be confused with the subscript of a scalar that denotes a component of the vector.5. Parsimonious games are the subset of constant sum homogeneous weighted majority games characterized by the parsimony property to have, for any given number n of non-dummy players in the game, the smallest number, i.e. exactly n, of minimal winning coalitions. For details see also [8].6. By induction: indeed it is immediate to check that (8) is true for t=1 and, if true for t, is true also for t+1.7. Note that the winning quota
(or (t+1)/2)).4. Henceforth the subscript of the vector is its dimension, not to be confused with the subscript of a scalar that denotes a component of the vector.5. Parsimonious games are the subset of constant sum homogeneous weighted majority games characterized by the parsimony property to have, for any given number n of non-dummy players in the game, the smallest number, i.e. exactly n, of minimal winning coalitions. For details see also [8].6. By induction: indeed it is immediate to check that (8) is true for t=1 and, if true for t, is true also for t+1.7. Note that the winning quota 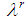 of
of 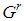 may well be greater than
may well be greater than 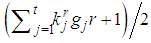 , i.e. for
, i.e. for 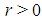 ,
, 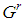 may not be constant sum.8. It is the counterpart of the "largest min win" coalition (in backward lexicographic order) of a weighted majority game defined in [10], pp. 312.9. By induction: it is true for j=0, and if true for j it is true for j+1.10. Note that for t=3 or 4 it is
may not be constant sum.8. It is the counterpart of the "largest min win" coalition (in backward lexicographic order) of a weighted majority game defined in [10], pp. 312.9. By induction: it is true for j=0, and if true for j it is true for j+1.10. Note that for t=3 or 4 it is 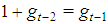 . Hence for such t:
. Hence for such t: 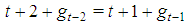 so that both (13) and (14) describe
so that both (13) and (14) describe 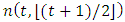 .
.
References
| [1] | Baron D.P., Ferejohn J.A., Bargaining in legislatures, American Political Science Review, 83, 1181-1206, 1989. |
| [2] | Isbell R., A class of majority games, Quarterly Journal of Mathematics, 7, 183-187, 1956. |
| [3] | Kalandrakis T., Proposal rights and political power, American Journal of Political Science,. 50(2), 441-448, 2006. |
| [4] | Le Breton M., Montero M., Zaporozhets V., Voting power in the EU council of ministers and fair decision making in distributive politics, Mathematical Social Sciences, 63, 159–173, 2012. |
| [5] | Montero M., Proportional Payoffs in Majority Games, Available at SSRN: http://ssrn.com/abstract=1112626, 2008. |
| [6] | Ostmann A., On the minimal representation of homogeneous games, International Journal of Game Theory, 16, 69-81, 1987. |
| [7] | Peleg B., On weights of constant-sum majority games, SIAM J. Appl. Math., 16(3), 527–532, 1968. |
| [8] | Pressacco F., Plazzotta G. and L. Ziani, Bilateral symmetry and modified Pascal triangles in Parsimonious games, available on http://hal.archives-ouvertes.fr/ with validation no.: hal-00948123, 2013. |
| [9] | Rosenmüller J., Weighted majority games and the matrix of Homogeneity. Operations Research, 28, 123-141, 1984. |
| [10] | Rosenmüller J., Homogeneous games: recursive structure and computation, Mathematics of Operations Research, 12(2), 309-330, 1987. |
| [11] | Schmeidler D., The Nucleolus of a Characteristic Function Game, SIAM Journal on Applied Mathematics,. 17(6), 1163-1170, 1969. |
| [12] | Von Neumann J. and O. Morgenstern, Theory of games and economic behaviour, Princeton University Press, 1947. |



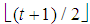 ; we describe unequivocally a Fibonacci game on the basis of its profile as a function of t and of a proper index z=1,…,
; we describe unequivocally a Fibonacci game on the basis of its profile as a function of t and of a proper index z=1,…,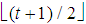 ; we provide rules concerning the behaviour of the total number n(t,z) of non-dummy players in a Fibonacci game. It turns out that there are two kinds of Fibonacci games, associated respectively with z=1 (Fibonacci-Isbell games) and z>1.
; we provide rules concerning the behaviour of the total number n(t,z) of non-dummy players in a Fibonacci game. It turns out that there are two kinds of Fibonacci games, associated respectively with z=1 (Fibonacci-Isbell games) and z>1.
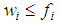 for any i=1,…,n). The second proposition ([2], third indent, p. 185) claimed that a game whose individual weights satisfied
for any i=1,…,n). The second proposition ([2], third indent, p. 185) claimed that a game whose individual weights satisfied 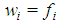 for any i=1,…,n-2,
for any i=1,…,n-2, 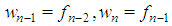 , described, for any n>2, a constant sum homogeneous weighted majority game with minimal winning quota
, described, for any n>2, a constant sum homogeneous weighted majority game with minimal winning quota  . Hence, in such games all the first n Fibonacci numbers are associated with all individual weights and the winning quota. On the basis of this connection we suggest to call Fibonacci-Isbell the set of games defined by the second proposition.Thinking in terms of type weights rather than of individual ones and keeping account that in any n person Fibonacci-Isbell game there are t=n-2 types of players, we argue that such games satisfy another slightly different "bridge" property: the bottom-top (strictly) ordered n-1 (or t+1) dimension vector of type weights and winning quota is a string of n-1 consecutive Fibonacci numbers starting from
. Hence, in such games all the first n Fibonacci numbers are associated with all individual weights and the winning quota. On the basis of this connection we suggest to call Fibonacci-Isbell the set of games defined by the second proposition.Thinking in terms of type weights rather than of individual ones and keeping account that in any n person Fibonacci-Isbell game there are t=n-2 types of players, we argue that such games satisfy another slightly different "bridge" property: the bottom-top (strictly) ordered n-1 (or t+1) dimension vector of type weights and winning quota is a string of n-1 consecutive Fibonacci numbers starting from 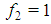 . In order to generalize this property to other feasible (n,t) combinations, we suggest to define Fibonacci games as the subset of constant sum homogeneous weighted majority games whose bottom-top increasing sequence of type weights and winning quota (in their minimal homogeneous representation) is a string of consecutive Fibonacci numbers1. Henceforth, it is convenient to use the (first order) "delayed" Fibonacci sequence g defined, for any natural n, by the relation
. In order to generalize this property to other feasible (n,t) combinations, we suggest to define Fibonacci games as the subset of constant sum homogeneous weighted majority games whose bottom-top increasing sequence of type weights and winning quota (in their minimal homogeneous representation) is a string of consecutive Fibonacci numbers1. Henceforth, it is convenient to use the (first order) "delayed" Fibonacci sequence g defined, for any natural n, by the relation 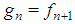 , and delayed Fibonacci subsequences
, and delayed Fibonacci subsequences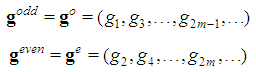 Moreover, following Rosenmüller ([10], p. 311), we take into consideration the "profile" of a constant sum homogeneous weighted majority game with t types denoted by the ordered vector
Moreover, following Rosenmüller ([10], p. 311), we take into consideration the "profile" of a constant sum homogeneous weighted majority game with t types denoted by the ordered vector 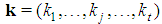 , whose component
, whose component 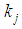 is the number of players of type j in the game.After that, it becomes clear that Fibonacci games are unequivocally described by feasible triplets
is the number of players of type j in the game.After that, it becomes clear that Fibonacci games are unequivocally described by feasible triplets 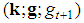 in which the profile k and the delayed Fibonacci sequence g share the dimension t, gj is the weight of players of type j, gt+1 is the winning quota and a triplet is feasible if it meets the homogeneity conditions (see [7], Theor. 3.5 and the “test” of homogeneity2 [9], Theor.1.4).In our paper, we give a simple but insightful characterization of the feasible profiles k of Fibonacci games with t types. The proof of such a characterization largely exploits fundamental properties of the delayed Fibonacci sequence (as for the necessary conditions) and the satellite game approach (in the sufficiency part).As a consequence, for any positive integer t, there are altogether3
in which the profile k and the delayed Fibonacci sequence g share the dimension t, gj is the weight of players of type j, gt+1 is the winning quota and a triplet is feasible if it meets the homogeneity conditions (see [7], Theor. 3.5 and the “test” of homogeneity2 [9], Theor.1.4).In our paper, we give a simple but insightful characterization of the feasible profiles k of Fibonacci games with t types. The proof of such a characterization largely exploits fundamental properties of the delayed Fibonacci sequence (as for the necessary conditions) and the satellite game approach (in the sufficiency part).As a consequence, for any positive integer t, there are altogether3 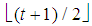 Fibonacci games, i.e. the Fibonacci-Isbell one and other
Fibonacci games, i.e. the Fibonacci-Isbell one and other 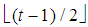 games. Moreover, it turns out that any two Fibonacci games with the same t have a different number n of non-dummy players. Hence, it seems logical to associate, for any t, the Fibonacci games with the set of integers
games. Moreover, it turns out that any two Fibonacci games with the same t have a different number n of non-dummy players. Hence, it seems logical to associate, for any t, the Fibonacci games with the set of integers 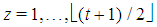 in such a way that the number n(t,z) of players (in the Fibonacci game with t types and index z) is an increasing function of z.A closed form description of the behavior of the function n(t,z) is also provided. It is surprising to verify that the derived function
in such a way that the number n(t,z) of players (in the Fibonacci game with t types and index z) is an increasing function of z.A closed form description of the behavior of the function n(t,z) is also provided. It is surprising to verify that the derived function 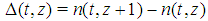 is resumed by a matrix whose columns are the entire delayed Fibonacci sequence (whose starting point is properly shifted down with z), while the rows are, in backward order, the delayed Fibonacci subsequences coherent with the parity of t (properly truncated, so as the row t has
is resumed by a matrix whose columns are the entire delayed Fibonacci sequence (whose starting point is properly shifted down with z), while the rows are, in backward order, the delayed Fibonacci subsequences coherent with the parity of t (properly truncated, so as the row t has 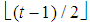 components).We are well aware of the existence of a vast body of literature concerning applications of homogeneous weighted majority games (constant as well as non-constant sum) to the analysis of voting power and committees interactions. Besides already cited papers, other examples may be found e.g. in Kalandrakis [3], Le Breton et al [4]. Yet we do not discuss applications of the Fibonacci games here in this or in other fields. Anyway, we anticipate that we have some preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.Yet we do not discuss applications of the Fibonacci games here in this or in other fields, but we anticipate that we have some (not yet published) preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.The plan of the paper is as follows: section 2 gives a short description of the basic notations used in the paper and recalls well known concepts of homogeneous weighted majority games; section 3 defines Fibonacci games and resumes the main results of the paper; section 4 provides an explicit description of the profiles of Fibonacci games for some small values of t; the behaviour of the n(t,z) and of
components).We are well aware of the existence of a vast body of literature concerning applications of homogeneous weighted majority games (constant as well as non-constant sum) to the analysis of voting power and committees interactions. Besides already cited papers, other examples may be found e.g. in Kalandrakis [3], Le Breton et al [4]. Yet we do not discuss applications of the Fibonacci games here in this or in other fields. Anyway, we anticipate that we have some preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.Yet we do not discuss applications of the Fibonacci games here in this or in other fields, but we anticipate that we have some (not yet published) preliminary evidence that interesting applications to the weighted voting systems in parliamentary elections may be obtained.The plan of the paper is as follows: section 2 gives a short description of the basic notations used in the paper and recalls well known concepts of homogeneous weighted majority games; section 3 defines Fibonacci games and resumes the main results of the paper; section 4 provides an explicit description of the profiles of Fibonacci games for some small values of t; the behaviour of the n(t,z) and of 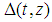 functions and their connections with the delayed Fibonacci (sub)sequences are presented and discussed in section 5; all the proofs are grouped in sections 6 and 7; conclusions follow in the final section 8.
functions and their connections with the delayed Fibonacci (sub)sequences are presented and discussed in section 5; all the proofs are grouped in sections 6 and 7; conclusions follow in the final section 8.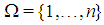 denote the set of non-dummy players of a simple constant sum game in characteristic function form. A simple game is a mapping
denote the set of non-dummy players of a simple constant sum game in characteristic function form. A simple game is a mapping 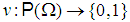 such that
such that 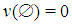 and
and 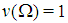 , and a coalition
, and a coalition 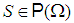 is winning if its payoff
is winning if its payoff 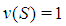 and losing otherwise. A simple game is constant sum if
and losing otherwise. A simple game is constant sum if 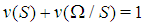 for any S. Moreover, S is minimal winning if, for any player
for any S. Moreover, S is minimal winning if, for any player 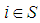 ,
, 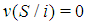 .A simple weighted majority game is described by the pair
.A simple weighted majority game is described by the pair 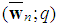 where4
where4 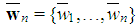 is the (weakly) ordered vector (
is the (weakly) ordered vector (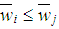 for i
for i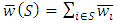 and
and 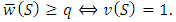 A simple constant sum homogeneous weighted majority game is described by its minimal homogeneous representation, that is the ordered vector
A simple constant sum homogeneous weighted majority game is described by its minimal homogeneous representation, that is the ordered vector 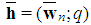 which meets the homogeneity conditions, that is
which meets the homogeneity conditions, that is 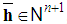 ,
, 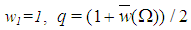 and
and 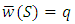 for any minimal winning coalition.The vector
for any minimal winning coalition.The vector 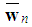 of the minimal homogeneous representation induces a decomposition of
of the minimal homogeneous representation induces a decomposition of 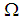 in equivalence classes K1,…,Kj,…,Kt.. Each class groups all players of the same type, sharing the same individual weight and the corresponding (strongly) ordered type weight vector is:
in equivalence classes K1,…,Kj,…,Kt.. Each class groups all players of the same type, sharing the same individual weight and the corresponding (strongly) ordered type weight vector is: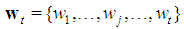 with
with 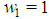 .Coherently,
.Coherently, 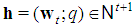 , but to unequivocally describe a game it is necessary also to introduce also the profile
, but to unequivocally describe a game it is necessary also to introduce also the profile 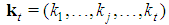 with
with 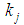 the number of players of type j in the game. Thus, a constant sum homogeneous weighted majority game is described by
the number of players of type j in the game. Thus, a constant sum homogeneous weighted majority game is described by 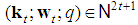 .Finally, we denote by
.Finally, we denote by 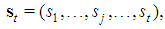 with
with 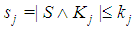 , the "profile" of the coalition S, so that
, the "profile" of the coalition S, so that 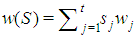 is an alternative formalization of the weight of S and, by homogeneity,
is an alternative formalization of the weight of S and, by homogeneity, 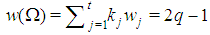 .
.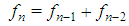 holding for any natural n>2 with initial conditions
holding for any natural n>2 with initial conditions 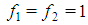 . Henceforth, we exploit the "delayed" Fibonacci sequence
. Henceforth, we exploit the "delayed" Fibonacci sequence 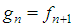 for any n, and denote, for any integer m, by
for any n, and denote, for any integer m, by 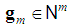 the vector
the vector 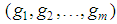 . Coherently, the denumerable sequence
. Coherently, the denumerable sequence 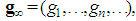 and
and 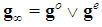 with
with 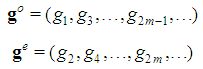 the two denumerable (sub)sequences obtained extracting from
the two denumerable (sub)sequences obtained extracting from 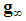 all elements of odd or, respectively, even index.Definition 3.1 The set of Fibonacci games is the subset of constant sum homogeneous weighted majority games with
all elements of odd or, respectively, even index.Definition 3.1 The set of Fibonacci games is the subset of constant sum homogeneous weighted majority games with 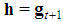 , that is
, that is 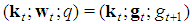 . Remark 3.1 Feasibility conditions require that in any Fibonacci game with t types,
. Remark 3.1 Feasibility conditions require that in any Fibonacci game with t types,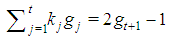 constant for any kt: the winning quota is the same for all Fibonacci games with the same t. Proof. Homogeneity requires that
constant for any kt: the winning quota is the same for all Fibonacci games with the same t. Proof. Homogeneity requires that 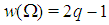 , i.e.
, i.e.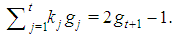
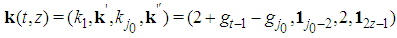
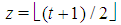 in order to have a complete indexation of the games, by:
in order to have a complete indexation of the games, by: 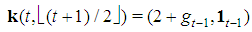
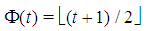
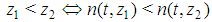 . Proofs of Th. 3.1 and 3.2 follow in sections 6 and 7.
. Proofs of Th. 3.1 and 3.2 follow in sections 6 and 7.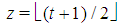 (the last vector of each row), all type components, except the bottom one, are 1, while this latter component plays a balancing role (according to Formula (2)); for all the other z, there is just one (non bottom) component equal to 2 in place
(the last vector of each row), all type components, except the bottom one, are 1, while this latter component plays a balancing role (according to Formula (2)); for all the other z, there is just one (non bottom) component equal to 2 in place 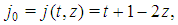 all the others (non bottom) are still 1 and, again, the bottom component plays the balancing role (according to Formula (1)).
all the others (non bottom) are still 1 and, again, the bottom component plays the balancing role (according to Formula (1)).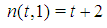
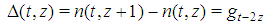
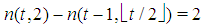
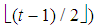 elements of the Fibonacci subsequence
elements of the Fibonacci subsequence 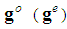 . In turn, the columns are nothing but the whole Fibonacci sequence
. In turn, the columns are nothing but the whole Fibonacci sequence 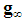 whose starting point is shifted at the row t=1+2z.
whose starting point is shifted at the row t=1+2z.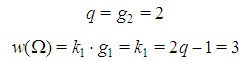 Hence there are three players with weight
Hence there are three players with weight 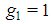 ,
, 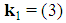 and
and 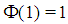 . For t=2:
. For t=2: 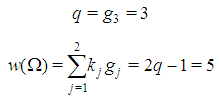 Hence,
Hence, 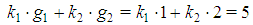 . There are two solutions
. There are two solutions 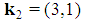 and
and 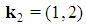 but the second is not feasible because the profile
but the second is not feasible because the profile 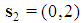 identifies a minimal winning coalition S with w(S)=4>q, incompatible with the homogeneous character. On the other side, the first solution is feasible with profiles (3,0) and (1,1) of the minimal winning coalitions, so that
identifies a minimal winning coalition S with w(S)=4>q, incompatible with the homogeneous character. On the other side, the first solution is feasible with profiles (3,0) and (1,1) of the minimal winning coalitions, so that 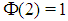 . For t>2, we show at first that the conditions (1) or (2) are necessary for Fibonacci games and then that they are also sufficient.
. For t>2, we show at first that the conditions (1) or (2) are necessary for Fibonacci games and then that they are also sufficient.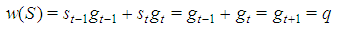 Property 6.2 In any Fibonacci game with t>1, kt=1. Proof. Otherwise the coalition S:st=(0t-1,2) would be minimal winning with
Property 6.2 In any Fibonacci game with t>1, kt=1. Proof. Otherwise the coalition S:st=(0t-1,2) would be minimal winning with 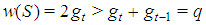 , a contradiction with the homogeneous character of the game. Property 6.3 In any Fibonacci game with t>2,
, a contradiction with the homogeneous character of the game. Property 6.3 In any Fibonacci game with t>2, 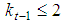 . Proof. Otherwise the coalition S:st=(0t-2,3,0) would be minimal winning as
. Proof. Otherwise the coalition S:st=(0t-2,3,0) would be minimal winning as 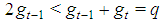 with
with 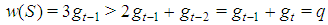 . Property 6.4 In any Fibonacci game with t>3, kt-2=1. Proof. Suppose on the contrary, kt-2>1and consider the coalition S:st=(0t-3,2,0,1). S would be minimal winning too as gt+gt-2
. Property 6.4 In any Fibonacci game with t>3, kt-2=1. Proof. Suppose on the contrary, kt-2>1and consider the coalition S:st=(0t-3,2,0,1). S would be minimal winning too as gt+gt-2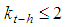 for h odd
for h odd 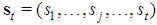 with
with 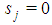 for j
for j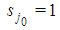 ;
; 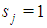 for j>j0 and
for j>j0 and 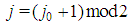 and
and 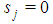 for j>j0 and
for j>j0 and 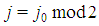 .Proof.
.Proof. 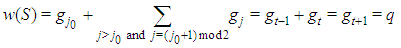 Now to prove Property 6.5 suppose on the contrary
Now to prove Property 6.5 suppose on the contrary 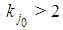 and consider the coalition
and consider the coalition 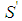 obtained from S by replacement of the player type
obtained from S by replacement of the player type 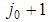 with two additional players of type
with two additional players of type 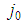 .
. 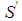 would be minimal winning with
would be minimal winning with 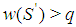 , a contradiction.Property 6.6 In any Fibonacci game it is
, a contradiction.Property 6.6 In any Fibonacci game it is 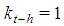 for h even
for h even 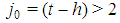 such that
such that 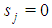 for
for 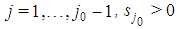 (so that a player of type
(so that a player of type 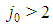 is the weakest in S), then kj0-1=1. Proof. Suppose on the contrary kj0-1>1 and consider the coalition
is the weakest in S), then kj0-1=1. Proof. Suppose on the contrary kj0-1>1 and consider the coalition 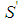 obtained from S by replacement of a player of type
obtained from S by replacement of a player of type 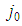 with two players of type
with two players of type 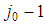 .
. 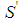 would be minimal winning with
would be minimal winning with 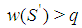 , a contradiction. This Lemma holds independently from the parity of h. Lemma 6.3 If a player of type j=t-h>2 is the weakest in a minimal winning coalition S, then there exists a minimal winning coalition
, a contradiction. This Lemma holds independently from the parity of h. Lemma 6.3 If a player of type j=t-h>2 is the weakest in a minimal winning coalition S, then there exists a minimal winning coalition 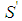 such that a player of type j-2 is the weakest in
such that a player of type j-2 is the weakest in 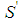 .Proof. In S replace the player of type j with the unique (by Lemma 6.2) player of type j-1 and one player of type j-2. Also this Lemma holds independently from the parity of h. Lemma 6.4 Suppose in a Fibonacci game
.Proof. In S replace the player of type j with the unique (by Lemma 6.2) player of type j-1 and one player of type j-2. Also this Lemma holds independently from the parity of h. Lemma 6.4 Suppose in a Fibonacci game 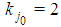 for j0=t-h with h odd <(t-1), then: a)
for j0=t-h with h odd <(t-1), then: a) 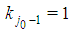 (by Property 6.6) and b) there is a minimal winning coalition
(by Property 6.6) and b) there is a minimal winning coalition 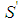 such that the player of type
such that the player of type 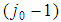 is its weakest player. Proof. (of part b))
is its weakest player. Proof. (of part b)) 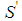 is obtained from the coalition S in Lemma 6.1 by replacement of the player of type t-(h-1) with one additional player of type t-h and the player of type t-(h+1). Clearly
is obtained from the coalition S in Lemma 6.1 by replacement of the player of type t-(h-1) with one additional player of type t-h and the player of type t-(h+1). Clearly 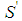 is minimal winning with
is minimal winning with 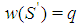 . Lemma 6.5 If in a Fibonacci game
. Lemma 6.5 If in a Fibonacci game 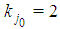 for j0=t-h with h odd <(t-1), then
for j0=t-h with h odd <(t-1), then 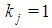 for any
for any 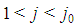 . Proof. Lemma 6.4 and Lemma 6.3 imply that there exists a set of minimal winning coalitions such that each player of type j,
. Proof. Lemma 6.4 and Lemma 6.3 imply that there exists a set of minimal winning coalitions such that each player of type j, 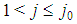 , is the weakest in a minimal winning coalition of the set. After that Lemma 6.5 comes as an immediate corollary of Lemma 6.2. Now, it is possible to give a more precise statement of Property 6.5 concerning the behaviour of
, is the weakest in a minimal winning coalition of the set. After that Lemma 6.5 comes as an immediate corollary of Lemma 6.2. Now, it is possible to give a more precise statement of Property 6.5 concerning the behaviour of 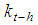 for h odd <(t-1). Indeed, Property 6.5 and Lemma 6.5 give immediately:Property 6.7 In a Fibonacci game there is at most one odd h<(t-1) such that
for h odd <(t-1). Indeed, Property 6.5 and Lemma 6.5 give immediately:Property 6.7 In a Fibonacci game there is at most one odd h<(t-1) such that 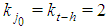 and
and 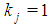 for all j>1 and
for all j>1 and 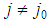 . Now by Remark 3.1 it is:
. Now by Remark 3.1 it is: 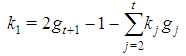
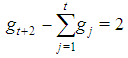
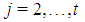 , kt satisfies conditions (1) or (2). In the first case and putting
, kt satisfies conditions (1) or (2). In the first case and putting 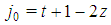 , we obtain:
, we obtain: 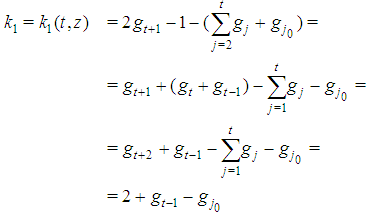
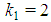 .In the second case, we get immediately:
.In the second case, we get immediately: 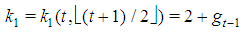
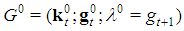 , "seed" game with
, "seed" game with 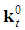 given by Formulas (1) or (2). In particular,
given by Formulas (1) or (2). In particular, 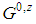 , seed game as a function of
, seed game as a function of 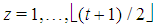 .•
.• 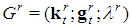 , any game of a r generation7 derived by the seed
, any game of a r generation7 derived by the seed 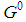 . Note that the dimension t of
. Note that the dimension t of 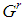 depends on r. Whenever useful, we utilize t(r). In particular,
depends on r. Whenever useful, we utilize t(r). In particular, 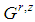 , game of a
, game of a 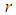 generation derived by the seed
generation derived by the seed 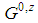 .• Feasible (not feasible) game: a
.• Feasible (not feasible) game: a 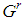 for which
for which 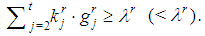 • For any given type index
• For any given type index 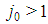 , an "intermediate" player in the game
, an "intermediate" player in the game 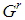 is a player of type
is a player of type 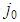 , a "large" player is a player of any type
, a "large" player is a player of any type 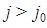 , a "small" player is any player of type
, a "small" player is any player of type 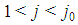 .• No bottom coalition of a feasible game
.• No bottom coalition of a feasible game 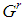 : a coalition
: a coalition 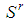 whose profile
whose profile 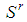 has
has 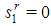 .• Dominant coalition8 of a feasible game
.• Dominant coalition8 of a feasible game 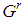 a coalition
a coalition 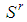 such that:(a)
such that:(a) 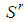 is no bottom(b) there is an index
is no bottom(b) there is an index 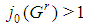 (or shortly
(or shortly 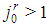 ) and a positive integer
) and a positive integer 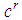 , such that
, such that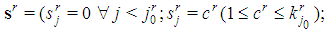
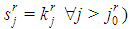 i.e.
i.e. 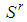 is made by all large players and by some (may be all) intermediate players, so that
is made by all large players and by some (may be all) intermediate players, so that 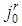 is the type index corresponding to the weakest player in the dominant coalition
is the type index corresponding to the weakest player in the dominant coalition 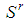 .(c)
.(c) 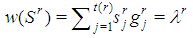 • Generation rules. Let
• Generation rules. Let 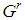 a feasible game,
a feasible game, 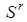 its dominant coalition and
its dominant coalition and 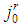 the corresponding type index. To any
the corresponding type index. To any 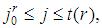 associate the game
associate the game 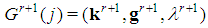 in which
in which 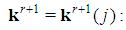 - for
- for 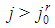 and
and 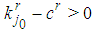 :
: 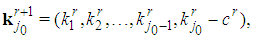 the dimension of
the dimension of 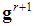 is j0 and
is j0 and 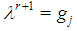 - for
- for 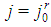 or
or 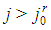 and
and 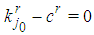 :
: 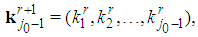 the dimension of
the dimension of 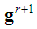 is
is 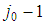 and
and 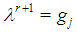 Verbally the dominant coalition
Verbally the dominant coalition 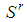 generates as many "satellite" games
generates as many "satellite" games 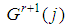 as the number of types j included in the coalition. The players of the satellite game associated with a type j are all players of type i
as the number of types j included in the coalition. The players of the satellite game associated with a type j are all players of type i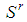 ; the winning quota is gj. The idea is that any satellite game looks for the dominant coalition of the satellite able to replace one player of type j in the generating game, while preserving the homogeneous character of the "seed" game. In turn, the dominant coalition gives rise to other satellite games of next generation and so on.Now, our adapted version of Basic Lemma is: Lemma 6.6 A seed weighted majority game
; the winning quota is gj. The idea is that any satellite game looks for the dominant coalition of the satellite able to replace one player of type j in the generating game, while preserving the homogeneous character of the "seed" game. In turn, the dominant coalition gives rise to other satellite games of next generation and so on.Now, our adapted version of Basic Lemma is: Lemma 6.6 A seed weighted majority game 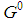 is homogeneous if, in the set of all
is homogeneous if, in the set of all 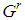 games obtained by the generation rules, do not exist feasible games lacking the dominant coalition. To prove the Lemma 6.6 we show that any game of the set
games obtained by the generation rules, do not exist feasible games lacking the dominant coalition. To prove the Lemma 6.6 we show that any game of the set 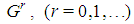 generated by a seed
generated by a seed 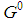 coherent with formulae (1) and (2) either is not feasible or admits a dominant coalition.
coherent with formulae (1) and (2) either is not feasible or admits a dominant coalition.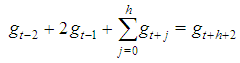
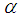 ):
): 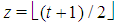 Let us denote
Let us denote 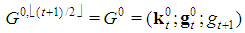 any seed game with
any seed game with 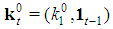 . The profile of the dominant coalition
. The profile of the dominant coalition 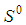 is
is 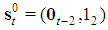 with
with 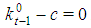 . Hence the satellite games associated with type t-1 and t are
. Hence the satellite games associated with type t-1 and t are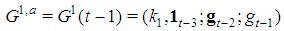 and
and 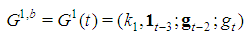 By Formula (8),
By Formula (8), 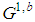 is not feasible, while
is not feasible, while 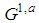 is feasible for any
is feasible for any 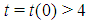 . Let us write briefly
. Let us write briefly 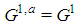 ; it is immediate to check that
; it is immediate to check that 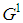 mimics the structure of
mimics the structure of 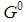 : only the dimension is different: it is
: only the dimension is different: it is 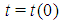 for
for 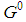 and
and 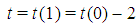 for
for 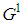 . The profile of the dominant coalition
. The profile of the dominant coalition 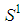 of
of 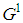 is
is 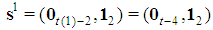 and the procedure may be recursively repeated until the integer r for which also
and the procedure may be recursively repeated until the integer r for which also 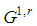 is no longer feasible. This is resumed by the following.Property 6.8 Let
is no longer feasible. This is resumed by the following.Property 6.8 Let 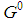 be a seed game of type
be a seed game of type 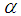 with t=t(0)>2. For any generation
with t=t(0)>2. For any generation 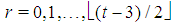 there is a unique feasible
there is a unique feasible 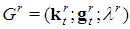 . The
. The 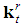 of such game is
of such game is 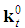 truncated at dimension tr=t(0)-2r, which is coherently the dimension of
truncated at dimension tr=t(0)-2r, which is coherently the dimension of 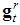 , while
, while 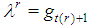 . Feasible
. Feasible 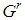 games have dominant coalition
games have dominant coalition 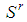 whose
whose 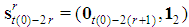 .
. 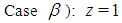 Let
Let 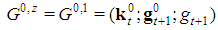 any seed game with
any seed game with 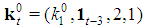 . The profile of the dominant coalition
. The profile of the dominant coalition 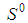 is still
is still 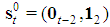 with
with 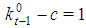 . Hence, the satellite games associated to type t-1 and t are
. Hence, the satellite games associated to type t-1 and t are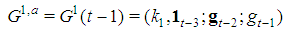 and
and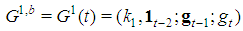 Both games share the properties of
Both games share the properties of 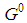 of case
of case 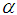 ), that is behave as seed games and generate for r=2,… sequences
), that is behave as seed games and generate for r=2,… sequences 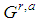 and
and 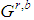 according to Property 6.8. Of course the dimension of
according to Property 6.8. Of course the dimension of 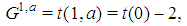 and of
and of 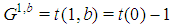 .
.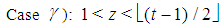 Let us write
Let us write 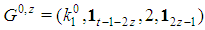 . The profile of the dominant coalition
. The profile of the dominant coalition 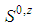 is
is 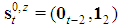 with
with 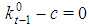 . Let us denote the two satellite games by
. Let us denote the two satellite games by 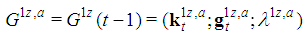 and
and 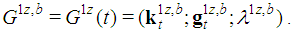 It is
It is 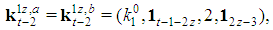
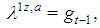 and
and 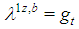 . Note that
. Note that 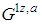 mimics
mimics 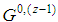 ; hence recursively we go back to
; hence recursively we go back to 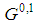 , i.e. the seed game of case
, i.e. the seed game of case 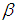 ).In turn, as by Formula (11),
).In turn, as by Formula (11), 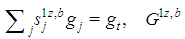 has dominant coalition with profile.
has dominant coalition with profile. 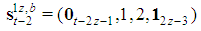 Hence
Hence 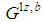 gives rise to 2z-1 satellite games
gives rise to 2z-1 satellite games 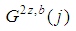 for
for 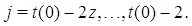 It is
It is 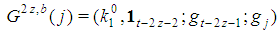 . By Formula (8), for all j, except
. By Formula (8), for all j, except 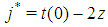 , the
, the 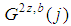 are not feasible; the survival feasible
are not feasible; the survival feasible 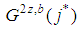 mimics the behavior of the
mimics the behavior of the 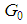 seed of the case
seed of the case 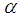 ).Summing up, in all three cases all
).Summing up, in all three cases all 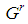 games either are not feasible, or if feasible admit a dominant coalition and the conditions of the Basic Lemma are verified.
games either are not feasible, or if feasible admit a dominant coalition and the conditions of the Basic Lemma are verified.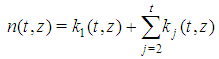
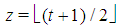 it is
it is 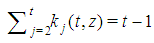 , by Formula (2) and
, by Formula (2) and 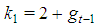 by Formula (10) so that:
by Formula (10) so that: 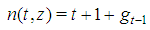
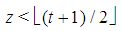 it is
it is 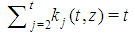 , by Formula (1) and
, by Formula (1) and 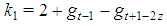 by Formula (9) so that:
by Formula (9) so that: 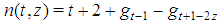
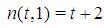 Proof. Proof of Property 5.2.For
Proof. Proof of Property 5.2.For 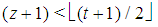 by Formula (14):
by Formula (14): 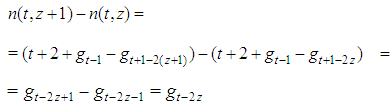
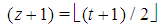 by Formulas (13) and (14):
by Formulas (13) and (14): 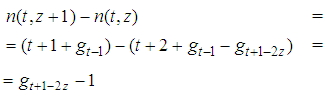
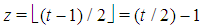 for t even and
for t even and  for t odd so that: t+1-2z=3 for t even and t+1-2z=2 for t oddwhich also means, on one side: t-2z=2 for t even and t-2z=1 for t odd
for t odd so that: t+1-2z=3 for t even and t+1-2z=2 for t oddwhich also means, on one side: t-2z=2 for t even and t-2z=1 for t odd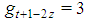 for t even and
for t even and 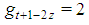 for t oddand finally
for t oddand finally 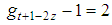 for t even and
for t even and 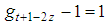 for t oddso that in both cases still
for t oddso that in both cases still 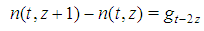
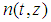 for any t and then, as a by product, gives a proof of Theorem 3.2. Proof. Proof of Property 5.3.Preliminarily note that putting
for any t and then, as a by product, gives a proof of Theorem 3.2. Proof. Proof of Property 5.3.Preliminarily note that putting 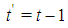 it is
it is 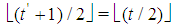 so that by Formula (13):
so that by Formula (13):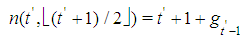
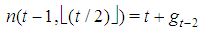 Moreover, it is by Formula (14) for t>4, or by Formula (13) for t=3 and 410
Moreover, it is by Formula (14) for t>4, or by Formula (13) for t=3 and 410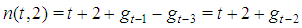 and immediately:
and immediately: 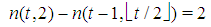
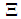 of values of n(t,z), z>1, a strictly monotone sequence is obtained. By Formulas (15), (17) and (19), all members of the sequence of first differences
of values of n(t,z), z>1, a strictly monotone sequence is obtained. By Formulas (15), (17) and (19), all members of the sequence of first differences  of the
of the 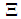 sequence are Fibonacci numbers (see Table 3).
sequence are Fibonacci numbers (see Table 3). 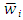 and either is exactly hit by the largest minimal winning coalition obtained by remaining players of smaller weight or the global weight of all these players is lower than
and either is exactly hit by the largest minimal winning coalition obtained by remaining players of smaller weight or the global weight of all these players is lower than 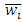 .3. As usual
.3. As usual 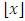 denotes the floor (x). In particular, for t integer even (odd),
denotes the floor (x). In particular, for t integer even (odd), 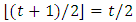 (or (t+1)/2)).4. Henceforth the subscript of the vector is its dimension, not to be confused with the subscript of a scalar that denotes a component of the vector.5. Parsimonious games are the subset of constant sum homogeneous weighted majority games characterized by the parsimony property to have, for any given number n of non-dummy players in the game, the smallest number, i.e. exactly n, of minimal winning coalitions. For details see also [8].6. By induction: indeed it is immediate to check that (8) is true for t=1 and, if true for t, is true also for t+1.7. Note that the winning quota
(or (t+1)/2)).4. Henceforth the subscript of the vector is its dimension, not to be confused with the subscript of a scalar that denotes a component of the vector.5. Parsimonious games are the subset of constant sum homogeneous weighted majority games characterized by the parsimony property to have, for any given number n of non-dummy players in the game, the smallest number, i.e. exactly n, of minimal winning coalitions. For details see also [8].6. By induction: indeed it is immediate to check that (8) is true for t=1 and, if true for t, is true also for t+1.7. Note that the winning quota 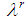 of
of 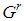 may well be greater than
may well be greater than 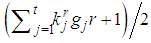 , i.e. for
, i.e. for  ,
,  may not be constant sum.8. It is the counterpart of the "largest min win" coalition (in backward lexicographic order) of a weighted majority game defined in [10], pp. 312.9. By induction: it is true for j=0, and if true for j it is true for j+1.10. Note that for t=3 or 4 it is
may not be constant sum.8. It is the counterpart of the "largest min win" coalition (in backward lexicographic order) of a weighted majority game defined in [10], pp. 312.9. By induction: it is true for j=0, and if true for j it is true for j+1.10. Note that for t=3 or 4 it is 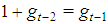 . Hence for such t:
. Hence for such t: 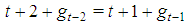 so that both (13) and (14) describe
so that both (13) and (14) describe 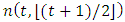 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML