Bodo Herzog
Economics Department, ESB Business School, Reutlingen University, Germany
Correspondence to: Bodo Herzog, Economics Department, ESB Business School, Reutlingen University, Germany.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A major lesson of the recent financial crisis is that money market freezes have major macroeconomic implications. This paper develops a tractable model in which we analyze the microeconomic and macroeconomic implications of a systemic banking crisis. In particular, we consider how the systemic crisis affects the optimal allocation of funding for businesses. We show that a central bank should reduce the interest rate to manage a systemic shock and hence smooth the macroeconomic consequences. Moreover, the analysis offers insight on the rational of bank behavior and the role of markets in a systemic crisis. We find that the failure to adopt the optimal policy can lead to economic fragility.
Keywords:
Financing Channels, Money-Market Freeze, Systemic Crises
Cite this paper: Bodo Herzog, Analyzing a Systemic Crisis in Finance, Journal of Game Theory, Vol. 4 No. 2, 2015, pp. 19-25. doi: 10.5923/j.jgt.20150402.01.
1. Introduction
The appropriate policy response to a contagious banking crisis is the subject of continuing and recent debates. A standard view is that monetary policy should play a role only if the financial disruption affects inflation or the real economy. Thus, we should not use monetary policy to alleviate financial distress if this policy impairs inflation and output. But is this argument an economic rational or merely an ideology?The standard view of central banking is challenged by the policy response during the recent financial crisis Woodford and Curdia [15]. It turned out that low interest rates are an essential instrument for limiting the threats of financial distress, which finally helps to stabilize the real economy. In August 2007, interest rates in both the United States (US) and European Union (EU) were cut dramatically. However, this policy is also challenged by Martin [9] who argues that central banks should provide liquidity at a penalty rate, even in severe crisis due to moral hazard.In order to understand the implications of systemic effects and the optimal decision- making of firms, it is important to take into consideration the macroeconomic linkage in respect to an interbank market freeze. We first analyze the choice problem between direct and intermediate finance in normal times, and later on under market distress. Since in practice, issuing debt is less expensive than bank loans, loan applicants are usually considered as those who cannot issue debt in the market. However, in a systemic banking crisis this trivial argument is probably wrong. Therefore, we expect a coexistence of both types of financial sources, however, with some bias to bond financing.This paper addresses the question: what is the optimal choice of financing in different states of the world.The rest of the paper is organized as follows: Section 2 presents a literature review. In Section 3, we build the model and discuss the results. Finally, section 4 concludes the paper.
2. Literature Review
The literature on systemic banking crises related to interbank markets, financing, and the micro-macro interaction is rather small. However, there is some related literature about the optimal allocation of bank loans and moral hazard. The work by Diamond [3], HolmstroÖm and Tirole [7] and Freixas and Jorge [5] show two important aspects relevant to our paper. Diamond [3] assumes limited participation of investors in the financial markets and justifies by this the coexistence of debt financing and bank loan financing. The limited participation implies that assets offered for sale in the market will not attract bids from all possible buyers and thus a lower sale price can be anticipated. As a consequence, they show that banks can emerge endogenously to solve the liquidity problem generated by limited participation.The contribution by HolmstrÖm and Tirole [7] studies directly the liquidity demand by firms. They show interesting results related to ours. This model shares a fundamental element with Diamond and Dybvig [4] that banks provide insurance against liquidity shocks. However, the demand for this insurance does not come from the risk aversion of depositors because in HolmstrÖm and Tirole [7] depositors are risk-neutral. The demand for liquidity insurance comes instead from firms, which are subject to moral hazard. The superiority of bank finance over direct or market finance lies in the commitment possibilities that banks have, and financial markets typically do not have. An exception of this commitment possibility, however, can be seen in the derivatives and structured markets. Obviously, this market segment was at the origin of the US–subprime crisis of 2007, in particular the origination of mortgage backed securities (MBS) and collateralized debt obligations (CDOs).A further aspect was studied by Bhattacharya and Chiesa [2] in the banking literature. They argue that a bilateral bank- borrower relationship may be superior to multilateral lending. Similar arguments are modeled along the same lines by Yosha [16, 17]. Finally, Kashyap et al. [8] find a new explanation for traditional deposit taking and lending in banking due to economies of scales. They argue that loan commitments, the contracts by which banks allow firms to borrow liquidity when they need it, are very similar to demand deposit contracts. In particular, the liquidity reserves held by banks can also be used as a buffer against the risk that firms draw on their credit lines. Moreover, they show that banks with large amounts of deposits are more likely to offer loan commitments.However, during the recent contagious crisis in the US and Europe, Reinhart and Rogoff [13] argue ’this time is different’. In a severe systemic crisis the behavior of banks as well as firms may not follow standard economic rationales. Consequently, we have study these new feedback loops and linkages to the macro-economy. We analyze these aspects in our paper. The stylized model is a promising approach because it allows us to analyze these feedback loops. Thus, the paper attempts to extend the existing game-theoretic banking literature.Our model sets itself apart from the standard banking literature: Firstly, we define an optimal allocation problem in normal times and later on under market distress; i.e. in a systemic or contagious crisis. Secondly, the model is tractable to analyze different solution mechanisms, for instance a systemic risk fund. Moreover, we are able to study current regulatory proposals for systemically important financial institutions (SIFIs). Thirdly, we analyze the first- and second- best economic outcomes. Finally, we find new policy conclusions, based on the modeling, for the design of a systemic risk fund.
3. Model
Consider an economy in which firms with zero wealth implement random investment projects of an initial investment size normalized to 1. The return of investment is 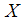 with probability
with probability 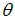 and zero otherwise. The firm has no other source of cash, so the repayment is zero if the investment fails. The riskless rate of interest is normalized to zero. Moreover, there is a continuum of such firms. However, there are two types of firms, good firms in a proportion
and zero otherwise. The firm has no other source of cash, so the repayment is zero if the investment fails. The riskless rate of interest is normalized to zero. Moreover, there is a continuum of such firms. However, there are two types of firms, good firms in a proportion 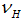 , which have a probability of success
, which have a probability of success 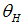 , and bad firms in a proportion of
, and bad firms in a proportion of 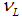 , which have a probability of success
, which have a probability of success 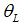 . We assume that
. We assume that 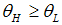 and
and 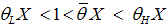 , where we define
, where we define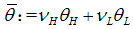 This parameter constellation assumes that only good (firm) projets have a positive net present value. Moreover, we assume that the proportion of firms
This parameter constellation assumes that only good (firm) projets have a positive net present value. Moreover, we assume that the proportion of firms 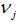 vary according to the parameter
vary according to the parameter 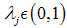 where
where 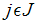 with
with 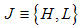 . Hence, in economically normal times there are more good than bad firms,
. Hence, in economically normal times there are more good than bad firms, 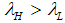 . Hence, we obtain
. Hence, we obtain 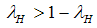 or
or 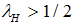 . Firms of type
. Firms of type 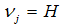 or
or 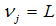 , are exposed to the same idiosyncratic liquidity shocks, however, with different size, such as
, are exposed to the same idiosyncratic liquidity shocks, however, with different size, such as 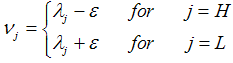 Where
Where 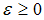 represent a systemic liquidity shock and
represent a systemic liquidity shock and 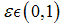 . That shock spills over to the real economy and therefore changes the quality and proportion of both good as well as bad firms in our economy.Furthermore, we assume that a liquidity shock,
. That shock spills over to the real economy and therefore changes the quality and proportion of both good as well as bad firms in our economy.Furthermore, we assume that a liquidity shock, 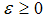 has an effect on the bank type: With a proportion of
has an effect on the bank type: With a proportion of 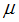 there are sound banks, i.e. banks fulfilling all capital requirements. The proportion of
there are sound banks, i.e. banks fulfilling all capital requirements. The proportion of 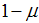 denotes the number of unsound banks, i.e. undercapitalized banks with risky investments1.Additionally, we assume in the beginning a competitive banking industry. Investors are assumed to be risk-neutral and they cannot distinguish between the two types of firms without of costs. Later on, we assume a monitoring technology to identify firm’s type with sunk costs per firm of
denotes the number of unsound banks, i.e. undercapitalized banks with risky investments1.Additionally, we assume in the beginning a competitive banking industry. Investors are assumed to be risk-neutral and they cannot distinguish between the two types of firms without of costs. Later on, we assume a monitoring technology to identify firm’s type with sunk costs per firm of 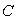 Finally, let
Finally, let 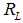 be the repayment on a bank loan by the firms and let
be the repayment on a bank loan by the firms and let 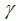 denote the proportion of good firms which are financing their investments via the market, i.e. corporate bonds.
denote the proportion of good firms which are financing their investments via the market, i.e. corporate bonds.
3.1. Model Discussion
The analysis begins with benchmark results, in order to compare these with the nonstandard findings later on. First, we start with the nominal interest rate of a bond issued by a firm.Proposition 1. The nominal bond interest rate 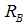 is less than the expected project return
is less than the expected project return 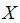 .Proof of Proposition 1. The bond has to repay an amount
.Proof of Proposition 1. The bond has to repay an amount 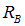 such that
such that 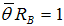 . This payment is feasible because
. This payment is feasible because 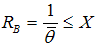 by the model assumption of
by the model assumption of 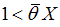 .Now, we take into account the banking sector. By paying a sunk cost
.Now, we take into account the banking sector. By paying a sunk cost 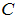 per firm at the initial period, banks are able to identify the firm’s type and then decide whether to lend. First under what conditions does the bank have an incentive to monitor the firm? Secondly, under what conditions will all good firms be attracted by competitive bank loan conditions? We define the probability of success of good firms that issue bonds as
per firm at the initial period, banks are able to identify the firm’s type and then decide whether to lend. First under what conditions does the bank have an incentive to monitor the firm? Secondly, under what conditions will all good firms be attracted by competitive bank loan conditions? We define the probability of success of good firms that issue bonds as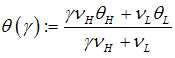 | (1) |
where 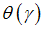 is the average probability of repayment. As intuition suggests, the average probability of repayment is increasing with the number of firms that issue bonds because only good firms are able to issue bonds.Proposition 2.
is the average probability of repayment. As intuition suggests, the average probability of repayment is increasing with the number of firms that issue bonds because only good firms are able to issue bonds.Proposition 2. 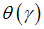 is increasing in
is increasing in 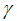 or in mathematical terms:
or in mathematical terms: 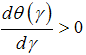 .Proof of Proposition 2. Calculate the first derivative of equation (1) in respect of
.Proof of Proposition 2. Calculate the first derivative of equation (1) in respect of 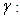
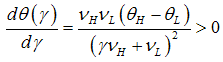 From this idea we obtain the value of the bond market interest rate
From this idea we obtain the value of the bond market interest rate 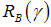 .Lemma 1. The bond market interest rate is given as:(i)
.Lemma 1. The bond market interest rate is given as:(i) 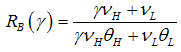 and(ii)
and(ii) 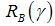 is decreasing in
is decreasing in 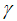 .Proof 1. The proof of part (i) follows immediately by using
.Proof 1. The proof of part (i) follows immediately by using 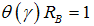 Part (ii) is proven by using the inverse of Proposition 2.Since
Part (ii) is proven by using the inverse of Proposition 2.Since 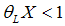 , we obtain in normal times that the condition
, we obtain in normal times that the condition 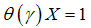 will be satisfied for some value
will be satisfied for some value 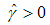 . Hence, banks will lend a certain amount that at least return the initial investment of 1. Of course, the bank lends only to good firms
. Hence, banks will lend a certain amount that at least return the initial investment of 1. Of course, the bank lends only to good firms 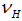 . So the profit will be given by
. So the profit will be given by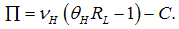 | (2) |
Individual rationality implies for all banks that they invest an amount of 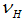 , such as
, such as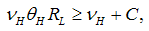 | (3) |
So the zero-profit condition in the perfect competitive banking market becomes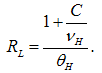 | (4) |
Proposition 3. The repayment rate on a bank loan 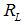 has the following properties:(i) The higher the success probability
has the following properties:(i) The higher the success probability 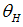 of the project, the lower the repayment rate
of the project, the lower the repayment rate 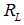 . In other words: The better the firms’ solvency, the better the credit conditions.(ii) The higher the screening costs
. In other words: The better the firms’ solvency, the better the credit conditions.(ii) The higher the screening costs 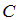 , the higher the repayment rate
, the higher the repayment rate 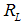 on a bank loan.(iii) If the number of good firms
on a bank loan.(iii) If the number of good firms 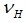 is large, the corresponding repayment rate
is large, the corresponding repayment rate 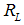 is less, due to more good firms with less risk in our economy, and thus economies of scale.Proof of Proposition 3. The proofs can be demonstrated by using equation (4)Now, we are ready to describe the three equilibrium constellations in relation to the parameter
is less, due to more good firms with less risk in our economy, and thus economies of scale.Proof of Proposition 3. The proofs can be demonstrated by using equation (4)Now, we are ready to describe the three equilibrium constellations in relation to the parameter  ; i.e. the proportion of bond issuing firms. Firstly, there is a banks–only equilibrium where
; i.e. the proportion of bond issuing firms. Firstly, there is a banks–only equilibrium where 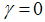 . Secondly, the bond market only equilibrium where
. Secondly, the bond market only equilibrium where 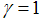 , and thirdly the mixed (bank and market) equilibrium where
, and thirdly the mixed (bank and market) equilibrium where 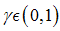 .Next, let me derive the three different equilibrium conditions. Banks–only equilibrium condition
.Next, let me derive the three different equilibrium conditions. Banks–only equilibrium condition 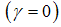 : The condition for such an equilibrium to exist requires:
: The condition for such an equilibrium to exist requires: 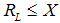 ; i.e. the loan is feasible. And
; i.e. the loan is feasible. And 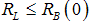 ; i.e. the loan is more attractive for borrowers. Since
; i.e. the loan is more attractive for borrowers. Since 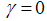 in the banks–only equilibrium the market for bonds does not exist or equivalently
in the banks–only equilibrium the market for bonds does not exist or equivalently 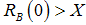 . Hence, only the first constraint is relevant. Using the zero-profit condition eq. (3), we obtain
. Hence, only the first constraint is relevant. Using the zero-profit condition eq. (3), we obtain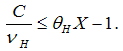 | (5) |
Bonds–only equilibrium condition 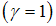 : Here, the condition is reversed, i.e.
: Here, the condition is reversed, i.e. 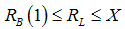 . Using the competitive values for
. Using the competitive values for 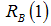 and
and 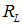 , the condition becomes
, the condition becomes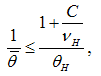 | (6) |
or equivalently,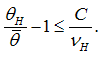 | (7) |
Mixed equilibrium condition: The mixed equilibrium is the interior solution in other words. The interior solution exists, in case of 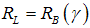 , which implies finally
, which implies finally 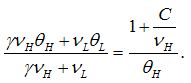 | (8) |
The unique solution of equation (8) is demonstrated in the following Lemma.Lemma 2. The unique 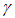 results in
results in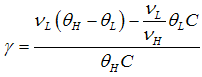 | (9) |
Proof 2. The proof is the solution of equation (8) in respect of 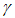 These findings offer interesting insights: Conditions (5) and (7) depend upon different parameters. It is possible that neither of them are satisfied (no funding to firms). In fact, this will occur when screening costs are too expensive and the proportion of good firms is too small. Otherwise, screening costs per unit are within the following interval
These findings offer interesting insights: Conditions (5) and (7) depend upon different parameters. It is possible that neither of them are satisfied (no funding to firms). In fact, this will occur when screening costs are too expensive and the proportion of good firms is too small. Otherwise, screening costs per unit are within the following interval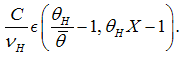 | (10) |
Hence, this condition describes the range of mixed equilibria. The next proposition summarizes the uniqueness and existence of the three equilibria conditions in our model.Proposition 4. There are three different equilibria conditions:(i) Banks–only equilibrium: The screening cost per unit of loan that is granted should be smaller with respect to the project’s present net value.(ii) Bonds–only equilibrium: The monitoring costs per unit of loan have to be excessively larger in comparison to the gains from screening; that allows an increase of a default probability of 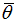 to a probability of
to a probability of 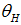 .(iii) Mixed equilibrium: The screening costs per unit of loans are in an interval determined by condition (10).Proof of Proposition 4. The existence proof of the equilibria conditions is divided in three parts: Part (i) and Part (ii) is trivial because part (i) follows directly from condition (5), and part (ii) follows immediately from condition (7). In part (iii), we use Lemma 1 together with part (ii). This proves the existence of the mixed equilibria, such as
.(iii) Mixed equilibrium: The screening costs per unit of loans are in an interval determined by condition (10).Proof of Proposition 4. The existence proof of the equilibria conditions is divided in three parts: Part (i) and Part (ii) is trivial because part (i) follows directly from condition (5), and part (ii) follows immediately from condition (7). In part (iii), we use Lemma 1 together with part (ii). This proves the existence of the mixed equilibria, such as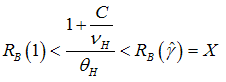
3.2. Macroeconomics
To evaluate the aggregate output for the three equilibria constellations, we aggregate the output over all firms and banks. All firms receive funding, if the firm is of type 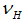 with a success probability in the interval
with a success probability in the interval 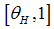 . The total output in the banks–only solution will be
. The total output in the banks–only solution will be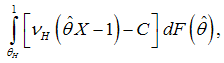 | (11) |
where 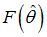 is a distribution function with
is a distribution function with 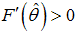 for all
for all 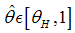 . Hence,
. Hence, 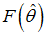 measures the proportion of good firms who’s success probability is above the threshold.Within the bonds–only equilibrium a fraction of negative net present value is implemented and the total output will be
measures the proportion of good firms who’s success probability is above the threshold.Within the bonds–only equilibrium a fraction of negative net present value is implemented and the total output will be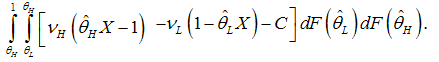 | (12) |
In case of the interior solution, the output will be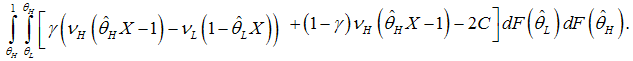 | (13) |
The last expression offers an interesting insight.Proposition 5. The mixed equilibrium is less efficient in comparison to bonds–only or banks–only equilibria due to duplication of screening costs.Proof of Proposition 5. The duplication of screening costs appears because firms identified as good will choose the bond market, despite the sunk costs of  . Consequently, the bonds–only or banks–only equilibria is more efficient for firms dependent on the type. The banks–only equilibrium which is servicing firms of type
. Consequently, the bonds–only or banks–only equilibria is more efficient for firms dependent on the type. The banks–only equilibrium which is servicing firms of type  is efficient, if and only if
is efficient, if and only if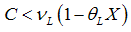 The last condition illustrates the case with lower monitoring costs than revenues for the inefficient firms of type
The last condition illustrates the case with lower monitoring costs than revenues for the inefficient firms of type 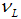 . The bonds–only equilibrium is efficient in the opposite case.
. The bonds–only equilibrium is efficient in the opposite case.
3.3. Systemic Crisis
In the following subsection, we include a systemic (shock) parameter ε in our standard model. We analyze the consequences in the three equilibrium constellations and the macroeconomic implications. Firstly, we describe the banks–only equilibrium. Using the zero-profit condition for banks, we obtain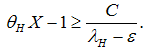 | (14) |
In case of a sufficiently large shock 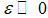 , and
, and 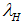 on the lower bound of the interval
on the lower bound of the interval 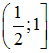 , the right-hand side of equation (14), convergences to infinity. Hence, the likelihood of the banks–only equilibrium is close to zero because the left-hand side, rep- resented by the net present value, is relatively small in a systemic crisis. Reason is the low success probability
, the right-hand side of equation (14), convergences to infinity. Hence, the likelihood of the banks–only equilibrium is close to zero because the left-hand side, rep- resented by the net present value, is relatively small in a systemic crisis. Reason is the low success probability 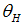 and low out- put
and low out- put 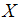 during a systemic crisis. In other words, in a systemic crisis the profitability and net present value (NPV) is too low, and hence there exists no banks–only equilibrium. Let me summarize this finding in the next proposition.Proposition 6. The banks–only equilibrium is less accessible during a systemic crisis.Proof of Proposition 6. Equation (14)This proposition demonstrates the fundamental problem during a systemic crisis or a sovereign debt crisis, such as in the Euro Area. In a systemic crisis, despite cheap refinancing conditions and low interest rates by central banks, almost all banks–only equilibria are eliminated. Thus central banks can not solve the financing problem alone. Again, the reasons are the high monitoring costs and the relatively low profitability of firms. Second, we illustrate the bonds–only equilibrium. Now, we rearrange equation (7) and obtain
during a systemic crisis. In other words, in a systemic crisis the profitability and net present value (NPV) is too low, and hence there exists no banks–only equilibrium. Let me summarize this finding in the next proposition.Proposition 6. The banks–only equilibrium is less accessible during a systemic crisis.Proof of Proposition 6. Equation (14)This proposition demonstrates the fundamental problem during a systemic crisis or a sovereign debt crisis, such as in the Euro Area. In a systemic crisis, despite cheap refinancing conditions and low interest rates by central banks, almost all banks–only equilibria are eliminated. Thus central banks can not solve the financing problem alone. Again, the reasons are the high monitoring costs and the relatively low profitability of firms. Second, we illustrate the bonds–only equilibrium. Now, we rearrange equation (7) and obtain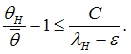 | (15) |
In case of large systemic shocks 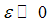 , the right-hand side will be large. Hence, the bonds–only equilibrium is easier to target and thus more likely. The question which remains open however is, whether there is sufficient demand of corporate bonds during a systemic crisis.Proposition 7. The bonds–only equilibrium is more accessible for firms in a systemic crisis.Proof of Proposition 7. Equation (15)However, due to market distress in a systemic crisis there is a weaker demand for bonds and other financial products. Consequently, putting together the result of Proposition 6 and Proposition 7, the mixed market equilibrium is most likely in a systemic crisis and this is despite the lower efficiency of the mixed equilibrium according to proposition 5.Before, studying the output implications, we address the following question: How can we get back to the standard banks– only equilibrium with higher welfare, even during a systemic crisis? Additionally, this is important for small and medium enter- prises with no access to the bond markets. Usually banks like to finance firms, because banks prefer debt finance due to higher profit margins in general. Bond issuing via banks is less attractive.Let
, the right-hand side will be large. Hence, the bonds–only equilibrium is easier to target and thus more likely. The question which remains open however is, whether there is sufficient demand of corporate bonds during a systemic crisis.Proposition 7. The bonds–only equilibrium is more accessible for firms in a systemic crisis.Proof of Proposition 7. Equation (15)However, due to market distress in a systemic crisis there is a weaker demand for bonds and other financial products. Consequently, putting together the result of Proposition 6 and Proposition 7, the mixed market equilibrium is most likely in a systemic crisis and this is despite the lower efficiency of the mixed equilibrium according to proposition 5.Before, studying the output implications, we address the following question: How can we get back to the standard banks– only equilibrium with higher welfare, even during a systemic crisis? Additionally, this is important for small and medium enter- prises with no access to the bond markets. Usually banks like to finance firms, because banks prefer debt finance due to higher profit margins in general. Bond issuing via banks is less attractive.Let 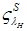 be an individual contribution from banks into a so-called’ systemic risk fund’. The whole fund is also guaranteed by the government and the fund is set up before the crisis; i.e. in period
be an individual contribution from banks into a so-called’ systemic risk fund’. The whole fund is also guaranteed by the government and the fund is set up before the crisis; i.e. in period 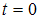 . All payments are collected and the systemic risk fund is accessible if and only if there is a systemic crisis. Now the new banks-only equilibrium with a systemic risk fund yields
. All payments are collected and the systemic risk fund is accessible if and only if there is a systemic crisis. Now the new banks-only equilibrium with a systemic risk fund yields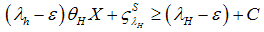 | (16) |
or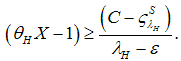 | (17) |
Thus, the systemic risk fund reduce the monitoring costs. Hence, the banks–only equilibrium is more likely, if the 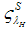 is sufficiently large in comparison to the monitoring costs. In the optimum, we obtain
is sufficiently large in comparison to the monitoring costs. In the optimum, we obtain 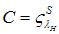 . Intuitively, the risk fund is a kind of insurance for banks, and simultaneously an insurance for the overall economy because it sustains the best equilibrium constellation even in crises times. Thus, the systemic risk fund can be seen as an explicit increase in the banks’ mark-up, and hence a rise of profitability for banks in a systemic crisis.Proposition 8. A systemic risk fund ensures the existence of the standard financing equilibrium.Proof of Proposition 8. Trivial derivation of condition (17)To obtain the standard equilibrium despite a systemic crisis, is in the interest of firms, banks, and the overall society due to macroeconomic efficiency. Furthermore, the good quality banks in our economy, with proportion
. Intuitively, the risk fund is a kind of insurance for banks, and simultaneously an insurance for the overall economy because it sustains the best equilibrium constellation even in crises times. Thus, the systemic risk fund can be seen as an explicit increase in the banks’ mark-up, and hence a rise of profitability for banks in a systemic crisis.Proposition 8. A systemic risk fund ensures the existence of the standard financing equilibrium.Proof of Proposition 8. Trivial derivation of condition (17)To obtain the standard equilibrium despite a systemic crisis, is in the interest of firms, banks, and the overall society due to macroeconomic efficiency. Furthermore, the good quality banks in our economy, with proportion 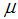 , use the optimal zero-profit condition in equation (16). In other words, they screen the successful companies and provide financing only to them. However at the same time, there are more risky or bad quality banks, in proportion of
, use the optimal zero-profit condition in equation (16). In other words, they screen the successful companies and provide financing only to them. However at the same time, there are more risky or bad quality banks, in proportion of 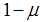 . They provide money to more risky firms with lower success probability and calculate the profits with the average success probability
. They provide money to more risky firms with lower success probability and calculate the profits with the average success probability 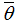 . Hence, in the banks–only equilibrium we obtain
. Hence, in the banks–only equilibrium we obtain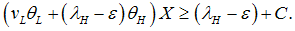 | (18) |
In terms of a perfect systemic shock 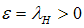 it simplifies to
it simplifies to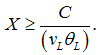 | (19) |
Suppose a systemic crisis increases the number of less profitable firms ceteris paribus, what will happen?Proposition 9. The banks–only equilibrium in a systemic crisis is more attractive for unsound banks.Proof of Proposition 9. The proof is by comparing the left-hand side of condition (18) in terms of a large systemic shock: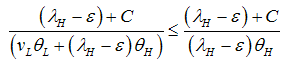 which is true due to the additional factor in the denominator on the left-hand side by
which is true due to the additional factor in the denominator on the left-hand side by 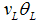 The higher the proportion of risky or greedy banks, the more likely is a banks–only equilibrium even in a systemic crisis. The optimal individual behavior of the different bank types’ imply interesting output consequences. Next, we calculate the output for a perfect systemic shock.Proposition 10. The welfare,
The higher the proportion of risky or greedy banks, the more likely is a banks–only equilibrium even in a systemic crisis. The optimal individual behavior of the different bank types’ imply interesting output consequences. Next, we calculate the output for a perfect systemic shock.Proposition 10. The welfare, 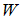 , of the economy in the banks–only equilibrium, during a perfect systemic shock, is dependent on the banks type and characterized by
, of the economy in the banks–only equilibrium, during a perfect systemic shock, is dependent on the banks type and characterized by 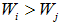 . In case of i, i.e.
. In case of i, i.e. 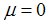 , there are unsound banks, and in equilibrium
, there are unsound banks, and in equilibrium 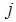 , there are sound banks.Proof of Proposition 10. Calculate the respective output functions
, there are sound banks.Proof of Proposition 10. Calculate the respective output functions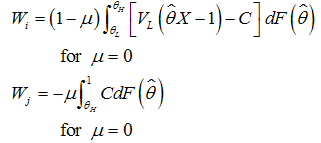 The comparison of both functions yields,
The comparison of both functions yields, 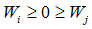 Hence, during a systemic shock the equilibrium in terms of macroeconomic output is more efficient if there are unsound banks. The reason for this is that unsound or risky banks provide more financing than the sound banks in particular in a systemic crisis. This phenomenon is known as the gambling of resurrection [6]. But this abnormal finding might help to sustain the macroeconomy.
Hence, during a systemic shock the equilibrium in terms of macroeconomic output is more efficient if there are unsound banks. The reason for this is that unsound or risky banks provide more financing than the sound banks in particular in a systemic crisis. This phenomenon is known as the gambling of resurrection [6]. But this abnormal finding might help to sustain the macroeconomy.
3.4. Policy Response
Now we analyze the policy response of fiscal and monetary policy in regard to a systemic crisis. We assume that the bank refinance its investments 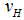 by the collection of
by the collection of 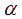 money from deposit holders and
money from deposit holders and 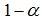 from the interbank market. The bank has to pay an interest rate
from the interbank market. The bank has to pay an interest rate 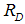 to the deposit holders and
to the deposit holders and 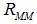 to the institutions in the money market or the central bank. Given only sound banks, we obtain
to the institutions in the money market or the central bank. Given only sound banks, we obtain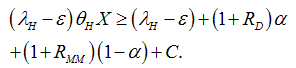 | (20) |
In normal times, 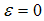 and
and 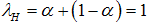 , and thus
, and thus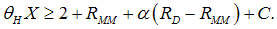 | (21) |
For an efficient equilibrium, we have to minimize the right-hand side.Proposition 11. The optimal policy in normal times equals 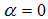 and
and 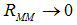 Proof of Proposition 11. Substitute
Proof of Proposition 11. Substitute 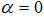 0 and
0 and 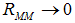 minimizes the right-hand side in equation (21)It implies that banks refinance the loans completely via the interbank market or the central bank. Here they just have to pay the interbank interest rate
minimizes the right-hand side in equation (21)It implies that banks refinance the loans completely via the interbank market or the central bank. Here they just have to pay the interbank interest rate 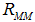 , which is close to zero. If there is a systemic shock, the condition (20) changes to
, which is close to zero. If there is a systemic shock, the condition (20) changes to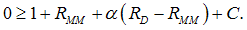 | (22) |
Proposition 12. There is no feasible refinancing banks–only equilibrium in a systemic crisis.Proof of Proposition 12. The left-hand side of equation (22) is always positive even if 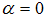 and the
and the 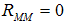 0. There are always screening costs
0. There are always screening costs 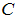 and fix costs. Thus, without a systemic risk fund there is no feasible banks–only equilibrium in a systemic crisis.Consequently, proposition (12) demonstrates that a systemic crisis must be tackled by joined fiscal and monetary policy.Hence, refinancing via deposit or interbank markets is difficult during a systemic crisis. This finding was prevalent in the past financial and economic crisis of 2007 to 2009. To remedy this disequilibrium constellation, we have to look for new mechanisms. We find an argument in favor of a systemic risk fund. Propositions (12) and (13) show that the interest rate cut by monetary policy to zero are a necessary, however, not sufficient condition during a systemic crisis.Although we cannot integrate all findings into a macro-economic model, our results suggest that joined fiscal and monetary policy is necessary in a systemic crisis. In addition, our findings are related to similar recent quantitative findings by Pindyck and Wang [11] and studies by Posner [12], Parson [10], Sunstein [14] and Allison [1]. These studies show that the risk of a national or global catastrophe is significant and should be taken more seriously. In particular, policymakers should devote greater resources to reduce the tail risk of a crisis. Our proposal is the implementation of a mandatory systemic risk fund which is established for all banks by all banks.
and fix costs. Thus, without a systemic risk fund there is no feasible banks–only equilibrium in a systemic crisis.Consequently, proposition (12) demonstrates that a systemic crisis must be tackled by joined fiscal and monetary policy.Hence, refinancing via deposit or interbank markets is difficult during a systemic crisis. This finding was prevalent in the past financial and economic crisis of 2007 to 2009. To remedy this disequilibrium constellation, we have to look for new mechanisms. We find an argument in favor of a systemic risk fund. Propositions (12) and (13) show that the interest rate cut by monetary policy to zero are a necessary, however, not sufficient condition during a systemic crisis.Although we cannot integrate all findings into a macro-economic model, our results suggest that joined fiscal and monetary policy is necessary in a systemic crisis. In addition, our findings are related to similar recent quantitative findings by Pindyck and Wang [11] and studies by Posner [12], Parson [10], Sunstein [14] and Allison [1]. These studies show that the risk of a national or global catastrophe is significant and should be taken more seriously. In particular, policymakers should devote greater resources to reduce the tail risk of a crisis. Our proposal is the implementation of a mandatory systemic risk fund which is established for all banks by all banks.
4. Conclusions
The systemic and especially macroeconomic aspects of financial crises remain unrecognized in the existing banking and finance literature. We develop a model that discusses thoroughly these aspects and the economic implications. In this paper, we identify new conditions for the optimal financing equilibrium in a systemic crisis. To tackle the problem of a credit market freeze during a contagious crisis, we propose to cut the interest rates and to utilize the idea of a systemic risk fund. Our model, however, has also limitations: (1) we do not look for alternatives, such as an enhanced macro-prudential regulation. (2) the model does not tackle the too-big-to-fail problem. Nevertheless, the model is tractable and informative with innovative insights for the current regulatory debate.
ACKNOWLEDGEMENTS
I thank the Editor and two anonymous referees for their helpful comments and suggestions. Research is funded by the RRI - Reutlingen Research Institute. This support is greatly appreciated.
Note
1. Some people call these banks ”greedy”.
References
| [1] | Allison, G. (2004). Nuclear Terrorism: The Ultimate Preventable Catastrophe. Henry Holt & Company. |
| [2] | Bhattacharya, S. and Chiesa, G. (1995). Proprietary information, financial intermediation and research incentives. Journal of Financial Intermediation, 4:328– 357. |
| [3] | Diamond, D. (1997). Liquidity, banks, and markets. Journal of Political Economy, 105(5):928–956. |
| [4] | Diamond, D. and Dybvig, P. (1983). Bank runs, deposit insurance, and liquidity. Journal of Political Economy, 91(3): 401–419. |
| [5] | Freixas, X. and Jorge, J. (2008). The role of interbank makrets in monetary policy: A model with rationing. JOurnla of Money, Credit and Banking, 40(6):1151–1176. |
| [6] | Hellwig, M. (1995). Systemic aspects of risk management in banking and finance. Swiss Journal of Economics and Statis- tics, 131(4/2):723–737. |
| [7] | HolmstrÖm, B. and Tirole, J. (1998). Private and public supply of liquidity. Journal of Political Economy, 106(1):1– 40. |
| [8] | Kashyap, A., Rajan, R., and Stein, J. (1999). Banks as liquidity providers: An explanation for the co-existence of lending and deposit taking. Discussion Paper, SSN, (156748). |
| [9] | Martin, A. (2009). Reconciling bagehot and the fed’s response to september 11. Journal of Money, Credit, and Banking, 41:397–415. |
| [10] | Parson, E. A. (2007). A review of richard posner’s catastrophe: Risk and response. Journal of Economic Literature, 45:147–164. |
| [11] | Pindyck, R. and Wang, N. (2009). The economic and policy consequences of catastrophes. MIT Sloan School Working Paper, (4751-09):1–26. |
| [12] | Posner, R. A. (2004). Catastrophe: Risk and Response. Oxford Universtiy Press. |
| [13] | Reinhart, C. M. and Rogoff, K. S. (2011). This Time Is Different: Eight Centuries of Financial Folly. Princeton. |
| [14] | Sunstein, C. R. (2007). Worst-Case Scenarios. Harvard University Press. |
| [15] | Woodford, M. and Curdia, V. (2010). Credit spreads and monetary policy. Journal of Money, Credit and Banking, 42(1):3–25. |
| [16] | Yosha, O. (1995a). Arm’s length financing and competition in product markets: A welfare analysis. Discussion Pa- per, Tel Avivi University, Israel. |
| [17] | Yosha, O. (1995b). Information disclosure costs and the choice of financing source. Journal of Financial Intermediation, 4:3–20. |

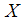 with probability
with probability 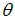 and zero otherwise. The firm has no other source of cash, so the repayment is zero if the investment fails. The riskless rate of interest is normalized to zero. Moreover, there is a continuum of such firms. However, there are two types of firms, good firms in a proportion
and zero otherwise. The firm has no other source of cash, so the repayment is zero if the investment fails. The riskless rate of interest is normalized to zero. Moreover, there is a continuum of such firms. However, there are two types of firms, good firms in a proportion 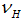 , which have a probability of success
, which have a probability of success 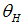 , and bad firms in a proportion of
, and bad firms in a proportion of 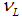 , which have a probability of success
, which have a probability of success 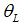 . We assume that
. We assume that 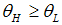 and
and 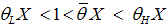 , where we define
, where we define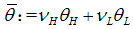 This parameter constellation assumes that only good (firm) projets have a positive net present value. Moreover, we assume that the proportion of firms
This parameter constellation assumes that only good (firm) projets have a positive net present value. Moreover, we assume that the proportion of firms 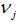 vary according to the parameter
vary according to the parameter 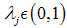 where
where 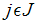 with
with 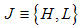 . Hence, in economically normal times there are more good than bad firms,
. Hence, in economically normal times there are more good than bad firms, 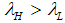 . Hence, we obtain
. Hence, we obtain 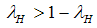 or
or 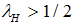 . Firms of type
. Firms of type 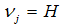 or
or 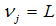 , are exposed to the same idiosyncratic liquidity shocks, however, with different size, such as
, are exposed to the same idiosyncratic liquidity shocks, however, with different size, such as 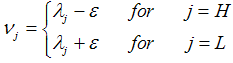 Where
Where 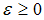 represent a systemic liquidity shock and
represent a systemic liquidity shock and 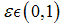 . That shock spills over to the real economy and therefore changes the quality and proportion of both good as well as bad firms in our economy.Furthermore, we assume that a liquidity shock,
. That shock spills over to the real economy and therefore changes the quality and proportion of both good as well as bad firms in our economy.Furthermore, we assume that a liquidity shock, 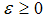 has an effect on the bank type: With a proportion of
has an effect on the bank type: With a proportion of 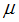 there are sound banks, i.e. banks fulfilling all capital requirements. The proportion of
there are sound banks, i.e. banks fulfilling all capital requirements. The proportion of 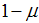 denotes the number of unsound banks, i.e. undercapitalized banks with risky investments1.Additionally, we assume in the beginning a competitive banking industry. Investors are assumed to be risk-neutral and they cannot distinguish between the two types of firms without of costs. Later on, we assume a monitoring technology to identify firm’s type with sunk costs per firm of
denotes the number of unsound banks, i.e. undercapitalized banks with risky investments1.Additionally, we assume in the beginning a competitive banking industry. Investors are assumed to be risk-neutral and they cannot distinguish between the two types of firms without of costs. Later on, we assume a monitoring technology to identify firm’s type with sunk costs per firm of 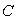 Finally, let
Finally, let 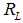 be the repayment on a bank loan by the firms and let
be the repayment on a bank loan by the firms and let 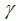 denote the proportion of good firms which are financing their investments via the market, i.e. corporate bonds.
denote the proportion of good firms which are financing their investments via the market, i.e. corporate bonds.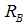 is less than the expected project return
is less than the expected project return 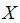 .Proof of Proposition 1. The bond has to repay an amount
.Proof of Proposition 1. The bond has to repay an amount 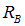 such that
such that 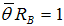 . This payment is feasible because
. This payment is feasible because 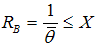 by the model assumption of
by the model assumption of 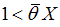 .Now, we take into account the banking sector. By paying a sunk cost
.Now, we take into account the banking sector. By paying a sunk cost 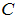 per firm at the initial period, banks are able to identify the firm’s type and then decide whether to lend. First under what conditions does the bank have an incentive to monitor the firm? Secondly, under what conditions will all good firms be attracted by competitive bank loan conditions? We define the probability of success of good firms that issue bonds as
per firm at the initial period, banks are able to identify the firm’s type and then decide whether to lend. First under what conditions does the bank have an incentive to monitor the firm? Secondly, under what conditions will all good firms be attracted by competitive bank loan conditions? We define the probability of success of good firms that issue bonds as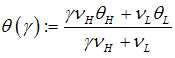
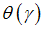 is the average probability of repayment. As intuition suggests, the average probability of repayment is increasing with the number of firms that issue bonds because only good firms are able to issue bonds.Proposition 2.
is the average probability of repayment. As intuition suggests, the average probability of repayment is increasing with the number of firms that issue bonds because only good firms are able to issue bonds.Proposition 2. 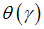 is increasing in
is increasing in 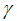 or in mathematical terms:
or in mathematical terms: 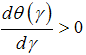 .Proof of Proposition 2. Calculate the first derivative of equation (1) in respect of
.Proof of Proposition 2. Calculate the first derivative of equation (1) in respect of 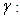
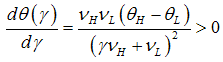 From this idea we obtain the value of the bond market interest rate
From this idea we obtain the value of the bond market interest rate 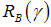 .Lemma 1. The bond market interest rate is given as:(i)
.Lemma 1. The bond market interest rate is given as:(i) 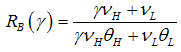 and(ii)
and(ii) 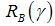 is decreasing in
is decreasing in 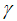 .Proof 1. The proof of part (i) follows immediately by using
.Proof 1. The proof of part (i) follows immediately by using 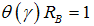 Part (ii) is proven by using the inverse of Proposition 2.Since
Part (ii) is proven by using the inverse of Proposition 2.Since 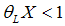 , we obtain in normal times that the condition
, we obtain in normal times that the condition 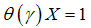 will be satisfied for some value
will be satisfied for some value 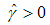 . Hence, banks will lend a certain amount that at least return the initial investment of 1. Of course, the bank lends only to good firms
. Hence, banks will lend a certain amount that at least return the initial investment of 1. Of course, the bank lends only to good firms 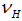 . So the profit will be given by
. So the profit will be given by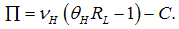
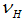 , such as
, such as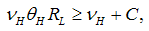
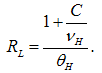
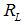 has the following properties:(i) The higher the success probability
has the following properties:(i) The higher the success probability 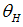 of the project, the lower the repayment rate
of the project, the lower the repayment rate 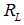 . In other words: The better the firms’ solvency, the better the credit conditions.(ii) The higher the screening costs
. In other words: The better the firms’ solvency, the better the credit conditions.(ii) The higher the screening costs 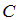 , the higher the repayment rate
, the higher the repayment rate 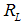 on a bank loan.(iii) If the number of good firms
on a bank loan.(iii) If the number of good firms 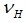 is large, the corresponding repayment rate
is large, the corresponding repayment rate 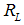 is less, due to more good firms with less risk in our economy, and thus economies of scale.Proof of Proposition 3. The proofs can be demonstrated by using equation (4)Now, we are ready to describe the three equilibrium constellations in relation to the parameter
is less, due to more good firms with less risk in our economy, and thus economies of scale.Proof of Proposition 3. The proofs can be demonstrated by using equation (4)Now, we are ready to describe the three equilibrium constellations in relation to the parameter  ; i.e. the proportion of bond issuing firms. Firstly, there is a banks–only equilibrium where
; i.e. the proportion of bond issuing firms. Firstly, there is a banks–only equilibrium where 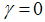 . Secondly, the bond market only equilibrium where
. Secondly, the bond market only equilibrium where 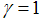 , and thirdly the mixed (bank and market) equilibrium where
, and thirdly the mixed (bank and market) equilibrium where 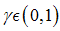 .Next, let me derive the three different equilibrium conditions. Banks–only equilibrium condition
.Next, let me derive the three different equilibrium conditions. Banks–only equilibrium condition 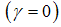 : The condition for such an equilibrium to exist requires:
: The condition for such an equilibrium to exist requires: 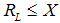 ; i.e. the loan is feasible. And
; i.e. the loan is feasible. And 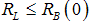 ; i.e. the loan is more attractive for borrowers. Since
; i.e. the loan is more attractive for borrowers. Since 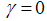 in the banks–only equilibrium the market for bonds does not exist or equivalently
in the banks–only equilibrium the market for bonds does not exist or equivalently 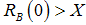 . Hence, only the first constraint is relevant. Using the zero-profit condition eq. (3), we obtain
. Hence, only the first constraint is relevant. Using the zero-profit condition eq. (3), we obtain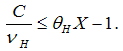
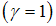 : Here, the condition is reversed, i.e.
: Here, the condition is reversed, i.e. 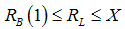 . Using the competitive values for
. Using the competitive values for 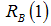 and
and 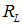 , the condition becomes
, the condition becomes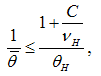
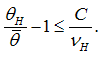
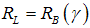 , which implies finally
, which implies finally 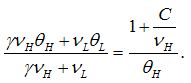
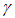 results in
results in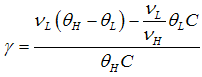
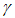 These findings offer interesting insights: Conditions (5) and (7) depend upon different parameters. It is possible that neither of them are satisfied (no funding to firms). In fact, this will occur when screening costs are too expensive and the proportion of good firms is too small. Otherwise, screening costs per unit are within the following interval
These findings offer interesting insights: Conditions (5) and (7) depend upon different parameters. It is possible that neither of them are satisfied (no funding to firms). In fact, this will occur when screening costs are too expensive and the proportion of good firms is too small. Otherwise, screening costs per unit are within the following interval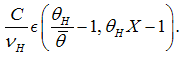
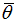 to a probability of
to a probability of 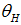 .(iii) Mixed equilibrium: The screening costs per unit of loans are in an interval determined by condition (10).Proof of Proposition 4. The existence proof of the equilibria conditions is divided in three parts: Part (i) and Part (ii) is trivial because part (i) follows directly from condition (5), and part (ii) follows immediately from condition (7). In part (iii), we use Lemma 1 together with part (ii). This proves the existence of the mixed equilibria, such as
.(iii) Mixed equilibrium: The screening costs per unit of loans are in an interval determined by condition (10).Proof of Proposition 4. The existence proof of the equilibria conditions is divided in three parts: Part (i) and Part (ii) is trivial because part (i) follows directly from condition (5), and part (ii) follows immediately from condition (7). In part (iii), we use Lemma 1 together with part (ii). This proves the existence of the mixed equilibria, such as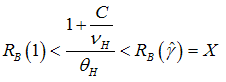
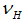 with a success probability in the interval
with a success probability in the interval 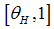 . The total output in the banks–only solution will be
. The total output in the banks–only solution will be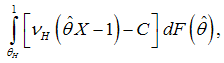
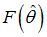 is a distribution function with
is a distribution function with 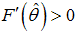 for all
for all 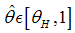 . Hence,
. Hence, 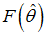 measures the proportion of good firms who’s success probability is above the threshold.Within the bonds–only equilibrium a fraction of negative net present value is implemented and the total output will be
measures the proportion of good firms who’s success probability is above the threshold.Within the bonds–only equilibrium a fraction of negative net present value is implemented and the total output will be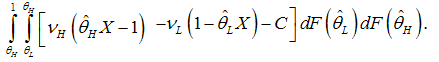
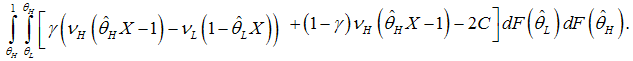
 . Consequently, the bonds–only or banks–only equilibria is more efficient for firms dependent on the type. The banks–only equilibrium which is servicing firms of type
. Consequently, the bonds–only or banks–only equilibria is more efficient for firms dependent on the type. The banks–only equilibrium which is servicing firms of type 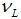 is efficient, if and only if
is efficient, if and only if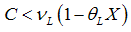 The last condition illustrates the case with lower monitoring costs than revenues for the inefficient firms of type
The last condition illustrates the case with lower monitoring costs than revenues for the inefficient firms of type 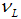 . The bonds–only equilibrium is efficient in the opposite case.
. The bonds–only equilibrium is efficient in the opposite case.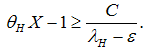
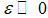 , and
, and 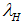 on the lower bound of the interval
on the lower bound of the interval 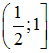 , the right-hand side of equation (14), convergences to infinity. Hence, the likelihood of the banks–only equilibrium is close to zero because the left-hand side, rep- resented by the net present value, is relatively small in a systemic crisis. Reason is the low success probability
, the right-hand side of equation (14), convergences to infinity. Hence, the likelihood of the banks–only equilibrium is close to zero because the left-hand side, rep- resented by the net present value, is relatively small in a systemic crisis. Reason is the low success probability 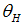 and low out- put
and low out- put 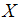 during a systemic crisis. In other words, in a systemic crisis the profitability and net present value (NPV) is too low, and hence there exists no banks–only equilibrium. Let me summarize this finding in the next proposition.Proposition 6. The banks–only equilibrium is less accessible during a systemic crisis.Proof of Proposition 6. Equation (14)This proposition demonstrates the fundamental problem during a systemic crisis or a sovereign debt crisis, such as in the Euro Area. In a systemic crisis, despite cheap refinancing conditions and low interest rates by central banks, almost all banks–only equilibria are eliminated. Thus central banks can not solve the financing problem alone. Again, the reasons are the high monitoring costs and the relatively low profitability of firms. Second, we illustrate the bonds–only equilibrium. Now, we rearrange equation (7) and obtain
during a systemic crisis. In other words, in a systemic crisis the profitability and net present value (NPV) is too low, and hence there exists no banks–only equilibrium. Let me summarize this finding in the next proposition.Proposition 6. The banks–only equilibrium is less accessible during a systemic crisis.Proof of Proposition 6. Equation (14)This proposition demonstrates the fundamental problem during a systemic crisis or a sovereign debt crisis, such as in the Euro Area. In a systemic crisis, despite cheap refinancing conditions and low interest rates by central banks, almost all banks–only equilibria are eliminated. Thus central banks can not solve the financing problem alone. Again, the reasons are the high monitoring costs and the relatively low profitability of firms. Second, we illustrate the bonds–only equilibrium. Now, we rearrange equation (7) and obtain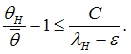
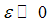 , the right-hand side will be large. Hence, the bonds–only equilibrium is easier to target and thus more likely. The question which remains open however is, whether there is sufficient demand of corporate bonds during a systemic crisis.Proposition 7. The bonds–only equilibrium is more accessible for firms in a systemic crisis.Proof of Proposition 7. Equation (15)However, due to market distress in a systemic crisis there is a weaker demand for bonds and other financial products. Consequently, putting together the result of Proposition 6 and Proposition 7, the mixed market equilibrium is most likely in a systemic crisis and this is despite the lower efficiency of the mixed equilibrium according to proposition 5.Before, studying the output implications, we address the following question: How can we get back to the standard banks– only equilibrium with higher welfare, even during a systemic crisis? Additionally, this is important for small and medium enter- prises with no access to the bond markets. Usually banks like to finance firms, because banks prefer debt finance due to higher profit margins in general. Bond issuing via banks is less attractive.Let
, the right-hand side will be large. Hence, the bonds–only equilibrium is easier to target and thus more likely. The question which remains open however is, whether there is sufficient demand of corporate bonds during a systemic crisis.Proposition 7. The bonds–only equilibrium is more accessible for firms in a systemic crisis.Proof of Proposition 7. Equation (15)However, due to market distress in a systemic crisis there is a weaker demand for bonds and other financial products. Consequently, putting together the result of Proposition 6 and Proposition 7, the mixed market equilibrium is most likely in a systemic crisis and this is despite the lower efficiency of the mixed equilibrium according to proposition 5.Before, studying the output implications, we address the following question: How can we get back to the standard banks– only equilibrium with higher welfare, even during a systemic crisis? Additionally, this is important for small and medium enter- prises with no access to the bond markets. Usually banks like to finance firms, because banks prefer debt finance due to higher profit margins in general. Bond issuing via banks is less attractive.Let 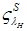 be an individual contribution from banks into a so-called’ systemic risk fund’. The whole fund is also guaranteed by the government and the fund is set up before the crisis; i.e. in period
be an individual contribution from banks into a so-called’ systemic risk fund’. The whole fund is also guaranteed by the government and the fund is set up before the crisis; i.e. in period  . All payments are collected and the systemic risk fund is accessible if and only if there is a systemic crisis. Now the new banks-only equilibrium with a systemic risk fund yields
. All payments are collected and the systemic risk fund is accessible if and only if there is a systemic crisis. Now the new banks-only equilibrium with a systemic risk fund yields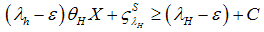
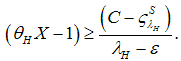
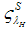 is sufficiently large in comparison to the monitoring costs. In the optimum, we obtain
is sufficiently large in comparison to the monitoring costs. In the optimum, we obtain 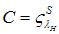 . Intuitively, the risk fund is a kind of insurance for banks, and simultaneously an insurance for the overall economy because it sustains the best equilibrium constellation even in crises times. Thus, the systemic risk fund can be seen as an explicit increase in the banks’ mark-up, and hence a rise of profitability for banks in a systemic crisis.Proposition 8. A systemic risk fund ensures the existence of the standard financing equilibrium.Proof of Proposition 8. Trivial derivation of condition (17)To obtain the standard equilibrium despite a systemic crisis, is in the interest of firms, banks, and the overall society due to macroeconomic efficiency. Furthermore, the good quality banks in our economy, with proportion
. Intuitively, the risk fund is a kind of insurance for banks, and simultaneously an insurance for the overall economy because it sustains the best equilibrium constellation even in crises times. Thus, the systemic risk fund can be seen as an explicit increase in the banks’ mark-up, and hence a rise of profitability for banks in a systemic crisis.Proposition 8. A systemic risk fund ensures the existence of the standard financing equilibrium.Proof of Proposition 8. Trivial derivation of condition (17)To obtain the standard equilibrium despite a systemic crisis, is in the interest of firms, banks, and the overall society due to macroeconomic efficiency. Furthermore, the good quality banks in our economy, with proportion 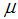 , use the optimal zero-profit condition in equation (16). In other words, they screen the successful companies and provide financing only to them. However at the same time, there are more risky or bad quality banks, in proportion of
, use the optimal zero-profit condition in equation (16). In other words, they screen the successful companies and provide financing only to them. However at the same time, there are more risky or bad quality banks, in proportion of 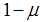 . They provide money to more risky firms with lower success probability and calculate the profits with the average success probability
. They provide money to more risky firms with lower success probability and calculate the profits with the average success probability 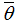 . Hence, in the banks–only equilibrium we obtain
. Hence, in the banks–only equilibrium we obtain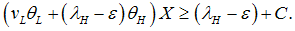
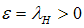 it simplifies to
it simplifies to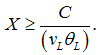
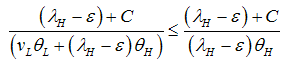 which is true due to the additional factor in the denominator on the left-hand side by
which is true due to the additional factor in the denominator on the left-hand side by 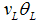 The higher the proportion of risky or greedy banks, the more likely is a banks–only equilibrium even in a systemic crisis. The optimal individual behavior of the different bank types’ imply interesting output consequences. Next, we calculate the output for a perfect systemic shock.Proposition 10. The welfare,
The higher the proportion of risky or greedy banks, the more likely is a banks–only equilibrium even in a systemic crisis. The optimal individual behavior of the different bank types’ imply interesting output consequences. Next, we calculate the output for a perfect systemic shock.Proposition 10. The welfare, 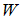 , of the economy in the banks–only equilibrium, during a perfect systemic shock, is dependent on the banks type and characterized by
, of the economy in the banks–only equilibrium, during a perfect systemic shock, is dependent on the banks type and characterized by 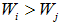 . In case of i, i.e.
. In case of i, i.e. 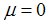 , there are unsound banks, and in equilibrium
, there are unsound banks, and in equilibrium 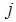 , there are sound banks.Proof of Proposition 10. Calculate the respective output functions
, there are sound banks.Proof of Proposition 10. Calculate the respective output functions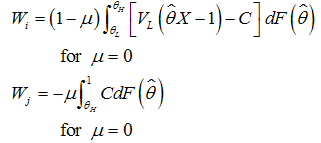 The comparison of both functions yields,
The comparison of both functions yields, 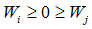 Hence, during a systemic shock the equilibrium in terms of macroeconomic output is more efficient if there are unsound banks. The reason for this is that unsound or risky banks provide more financing than the sound banks in particular in a systemic crisis. This phenomenon is known as the gambling of resurrection [6]. But this abnormal finding might help to sustain the macroeconomy.
Hence, during a systemic shock the equilibrium in terms of macroeconomic output is more efficient if there are unsound banks. The reason for this is that unsound or risky banks provide more financing than the sound banks in particular in a systemic crisis. This phenomenon is known as the gambling of resurrection [6]. But this abnormal finding might help to sustain the macroeconomy. by the collection of
by the collection of 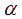 money from deposit holders and
money from deposit holders and 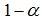 from the interbank market. The bank has to pay an interest rate
from the interbank market. The bank has to pay an interest rate 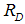 to the deposit holders and
to the deposit holders and 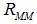 to the institutions in the money market or the central bank. Given only sound banks, we obtain
to the institutions in the money market or the central bank. Given only sound banks, we obtain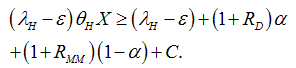
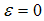 and
and 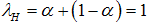 , and thus
, and thus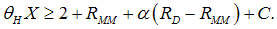
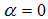 and
and 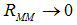 Proof of Proposition 11. Substitute
Proof of Proposition 11. Substitute 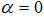 0 and
0 and 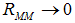 minimizes the right-hand side in equation (21)It implies that banks refinance the loans completely via the interbank market or the central bank. Here they just have to pay the interbank interest rate
minimizes the right-hand side in equation (21)It implies that banks refinance the loans completely via the interbank market or the central bank. Here they just have to pay the interbank interest rate 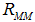 , which is close to zero. If there is a systemic shock, the condition (20) changes to
, which is close to zero. If there is a systemic shock, the condition (20) changes to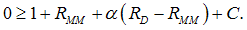
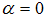 and the
and the 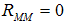 0. There are always screening costs
0. There are always screening costs 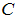 and fix costs. Thus, without a systemic risk fund there is no feasible banks–only equilibrium in a systemic crisis.Consequently, proposition (12) demonstrates that a systemic crisis must be tackled by joined fiscal and monetary policy.Hence, refinancing via deposit or interbank markets is difficult during a systemic crisis. This finding was prevalent in the past financial and economic crisis of 2007 to 2009. To remedy this disequilibrium constellation, we have to look for new mechanisms. We find an argument in favor of a systemic risk fund. Propositions (12) and (13) show that the interest rate cut by monetary policy to zero are a necessary, however, not sufficient condition during a systemic crisis.Although we cannot integrate all findings into a macro-economic model, our results suggest that joined fiscal and monetary policy is necessary in a systemic crisis. In addition, our findings are related to similar recent quantitative findings by Pindyck and Wang [11] and studies by Posner [12], Parson [10], Sunstein [14] and Allison [1]. These studies show that the risk of a national or global catastrophe is significant and should be taken more seriously. In particular, policymakers should devote greater resources to reduce the tail risk of a crisis. Our proposal is the implementation of a mandatory systemic risk fund which is established for all banks by all banks.
and fix costs. Thus, without a systemic risk fund there is no feasible banks–only equilibrium in a systemic crisis.Consequently, proposition (12) demonstrates that a systemic crisis must be tackled by joined fiscal and monetary policy.Hence, refinancing via deposit or interbank markets is difficult during a systemic crisis. This finding was prevalent in the past financial and economic crisis of 2007 to 2009. To remedy this disequilibrium constellation, we have to look for new mechanisms. We find an argument in favor of a systemic risk fund. Propositions (12) and (13) show that the interest rate cut by monetary policy to zero are a necessary, however, not sufficient condition during a systemic crisis.Although we cannot integrate all findings into a macro-economic model, our results suggest that joined fiscal and monetary policy is necessary in a systemic crisis. In addition, our findings are related to similar recent quantitative findings by Pindyck and Wang [11] and studies by Posner [12], Parson [10], Sunstein [14] and Allison [1]. These studies show that the risk of a national or global catastrophe is significant and should be taken more seriously. In particular, policymakers should devote greater resources to reduce the tail risk of a crisis. Our proposal is the implementation of a mandatory systemic risk fund which is established for all banks by all banks. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML