-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2015; 4(1): 6-12
doi:10.5923/j.jgt.20150401.02
Berge-Bacharach-Schelling Play
Romar Correa
Department of Economics, University of Mumbai, Mumbai, India
Correspondence to: Romar Correa, Department of Economics, University of Mumbai, Mumbai, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
We play coordination games. The Nash Equilibrium (NE) is not usually the cooperative solution. According to the definition, playerchooses a strategy from her strategy set given the vector of strategies of all the other players jin the NE. The Berge Equilibrium (BE) provides the cooperative outcome in many coordination contexts. Now, the ‘choice vector’ for player i is the vector of strategies of all the other players, given player i’s strategy in the BE. The NE and BE coexist. The contribution of Michael Bacharach and Thomas Schelling is the observation that people in a large number of situations do settle on a cooperative equilibrium. The solution is arrived at in the face of the fact that players distinguish between strategies even when the payoffs are identical. We explore the Helly metric that underlies the NE and BE. The metric does not satisfy the ‘separation of points’ criterion of Bacharach and Schelling. We take the step from Nash-Berge to Bacharach-Schelling by specifying a metric. The metric indicates the possibility of a leader in situations when different strategies provide identical payoffs. While all the other players distinguish between the strategies, the leader is the one who is indifferent and proposes a solution.
Keywords: Multiple equilibria, Leadership
Cite this paper: Romar Correa, Berge-Bacharach-Schelling Play, Journal of Game Theory, Vol. 4 No. 1, 2015, pp. 6-12. doi: 10.5923/j.jgt.20150401.02.
1. Introduction
- The title bears the names of three game theorists who reflected deeply on the foundations of the subject although they worked outside the mainstream. Thomas Schelling is best known and not just because he won the Nobel Prize. The seminal idea of focal points still remains hard to model. The empirical fact, supported by his stimulating examples, that in one-time settings people will come together and solve coordination problems is not easy to capture analytically. Schelling connects with Michael Bacharach along this dimension (see [1] for recent developments). In order to develop the thematic relation we consider the ‘pure coordination game’ or what Bacharach called the Schelling game:
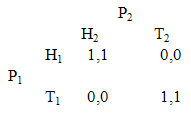 In this ‘Heads’ and ‘Tails’ game, if both players P1 and P2 concatenate their calls on the same face of a coin they earn a billion dollars each. Otherwise, they earn nothing. How does a reader with a knowledge of elementary game theory approach this problem? Surely, in Nash terms. That is, she will work out the optimal choice of row for P1 for all possible choices of columns of P2, and symmetrically the optimal choice of column for P2 for all possible choices of rows of P1. In the present case, both the diagonal terms are equilibria. Claude Berge, the mathematician, invited the profession to look at the problem in ‘complementary’ terms. Imagine P1 optimizing over columns, given the choices of rows, and P2 optimizing over rows, given the choices of columns. Berge was at the right time at the right place, Princeton in the earlier heyday of game theory. Yet, his ideas were met with less than enthusiasm. Language was partly to blame (not all his French writings are translated) and partly his terse mathematical exposition was not appreciated by economists. It is only in recent years that scholars have evinced interest in his work. On the one hand, mathematicians have refined and extended his results [2]. The agenda was, to some extent, given. For instance, the assumptions of quasi-concavity and upper semicontinuity had to be directed to the product strategy space of the other players j from the strategy set of player i. Greater expectations have been laid on his results by social scientists because a Berge Equilibrium (BE) provides the cooperative outcome in the standard illustrations in which the Nash Equilibrium (NE) does not [3], [4]. The population of social scientists referred to does not include economists and the reason is not far to seek. Why should agent i maximize over the choices of others? Edna Ullman-Margalit offers a minimal requirement in “considerateness” defined as actions designed to decrease the discomfort of others at trivial costs to oneself [5]. The ‘others’ could be anonymous as well as familiar. Gratitude may or may not result but reciprocity is expected. Considerateness can be distinguished from other well-known notions. Thus, ‘altruism’ is the case when the costs and benefits to others are significant. Considerateness is the minimal acknowledgement of the existence of the other qua respect for others as human beings and falls short of ‘kindness’. The expectation is that others are considerate but, at the same time, the considerate act of the agent contributes towards fostering such an environment. In the literature, players are free to play Nash or Berge. The state of the art is one in which both outcomes are possible and a set of theorems connects the two concepts. For instance, the two-player Prisoner’s Dilemma is a special case of the n-person Prisoner’s Dilemma. In both cases, defection is the unique NE and cooperation is the unique BE. The NE represents the individualistic idea within interdependence theory while the BE stands for the social value orientation within that theory. According to what has been called self-construal, individuals are both independent selves and interdependent selves [6]. Prosocial behavior is typically associated with the interdependent self. People imbued with characteristics like benevolence usually expect others to be similarly disposed. Situational triggers will activate one self or the other. In the study referred to, experiments were conducted to show that the selves could be manipulated. In this regard, scholars distinguish between moral sentiments and other-regarding preferences [4]. According to the latter, individual utility functions have two arguments, one concerned with self-welfare, the second with the welfare of others. Both Nash and Berge behavior rules can be rationalized according to this extended definition. The reference to moral sentiments leads to Adam Smith’s Theory of Moral Sentiments from which the evolution from BE to NE and back in historical time can be traced [7]. Till the eighteenth century, the understanding was that individuals recognized their fellow-beings as extensions of themselves. With the onset of the theory of social Darwinism, empathy was substituted by models emphasizing individual fitness which, more often than not, led to suboptimal competitive interactions between people. The end of the last century and the beginning of the present have witnessed a renewed interest in social interactions on foundations other than self-interest. Current thinking in all strains of Darwinist reasoning is cast in terms of the information content of specific instructions in guiding evolution [8-10]. For instance, the influence of the philosopher Herbert Spencer, who coined the term ‘the survival of the fittest’, lingers. However, similar to the case made by the economist-sociologist Thorstein Veblen, he argued that the survival of the fittest required policy interventions. Spencer’s model was moral. His biology was adaptationist, requiring both inheritance as well as acquired characteristics. It is this perspective, rather than social Darwinism, that has stood the test of time. Through sympathy, an agent places herself in the skin of other agents and experiences what she would feel if she was actually in their situations. The movement is instantaneous and triggered by specific circumstances. If the feelings coincide in the particular game, agent i will cooperate with agents j. However, if they do not, agent i will ‘defect’. Sympathy is the basis of moral judgments. Both Nash and Berge norms are internalized.In the NE the rational agent attempts to achieve the best-act profile by choosing only one component of the profile. The BE makes the substitution that it is the best-act profile of the others that the individual deliberates over. What is parametric in NE is choice-theoretic in BE and vice versa. Michael Bacharach and Thomas Schelling worked with the idea that agents choose whole profiles. In terms of our example, it is unnecessary, then, to dwell on P1 and P2. We need to ‘think inside the box’. Between themselves, agents implement their profile choices. If all play their part in the solution vector it will be unique. Bacharach and Schelling pioneered reasoning in one-shot engagements. Attempts to understand Bacharach’s ‘team reasoning’ have run the gamut from philosophy to neuroscience [11]. Players might obey Kant’s categorical imperative: Do unto others as you would have others do unto you [12], [13]. The effectiveness of a strategy depends upon the others who adopt it. Thus, deviation in a prisoner’s dilemma is inconsistent. Players deviate to gain, not to lose. If deviation is universalized, all lose. In other words, the equilibrium does not satisfy Al-Suwalem’s criterion of universalizability. Other criteria offered to distinguish ecological or social rationality from individual rationality include ‘reversibility’. Accordingly, in two-player games actions are chosen which are optimal if each player put herself in the other’s shoes. The axiom is extended to groups by iterating the rule. The ‘reversible rule’ thus becomes universalizable. Neuroscience contributes ‘empathy’. ‘Mirror neurons’ enable a player to identify with others. Feelings and emotions connect spontaneously. It is more costly for the neural system to isolate feelings than to relate to interacting parties. Our brains are hardwired with cooperative mechanisms. A final precept is the axiom of ‘symmetry or invariance under the permutation of individuals’. Players displaying groupthink search for a profile of strategies that maximizes the collective payoffs of the group. That profile need not be a Nash equilibrium. If one payoff Pareto-dominates the others, that payoff clearly maximizes the collective payoff. If the optimizing payoff is unique, members of the team play their component strategies in the profile. If not, the theory is indeterminate.Returning to our motivating example, Bacharach and Schelling were inspired, above all, by the fact of life that people, in general, solve cooperation problems. Complexity is introduced in the ‘Heads’ and ‘Tails’ game by the assumption that ‘Heads’ and ‘Tails’ might resonate differently for P1 and P2. They do not flip an unbiased coin to decide. Yet, Bacharach reports that people, in an overwhelming number of instances, call ‘Heads’. ‘Heads’, he suggests, possesses a different ‘salience’ from ‘Tails’. The experiments and tests could be replicated across cultures and time and space and, it is possible, ‘Tails’ is called out in a majority of those instances. The point remains. The problem is, in general, solved. In sum, the intuition connecting the three scientists in the title of the paper is the cooperative solution in one-shot coordination games. How might we get the northwest solution in the box above? Schelling would have suggestive numbers in that corner. Bacharach would argue that while both players might have different mental frames, one favoring ‘Heads’, the other ‘Tails’, the orientations are flexible. As an illustration of we-thinking they would modify their impulses to arrive at the solution ‘Heads’. Recently, Oded Stark [14] has proposed that in an economics of others, players change off-diagonal elements in the one-shot Prisoner’s Dilemma so as to coordinate on the best outcome. We develop the idea that a mediator is sufficient to lead the way to ‘Heads’. Schelling suggests the possibility of a leader, [15, p.91], Bacharach a director (albeit from outside the game) [16, p.123]. Bacharach offers the notion of myopia by means of which leaders/directors collapse the variable frames of all the players to a point [16, p.86]. The current development of the idea runs independent of the concepts surrounding reward and punishment [17]. Dictators in the famous game that bears that name turn out to be “generous” in reality. Their concern, primarily, is to preserve the pie and maximize social welfare. Mathematically, different ways of seeing a matrix game translates into different metrics players might impose between pairs of strategies. We revisit the Helly metric that underpins the NE. That metric does not enable the players to distinguish between Heads and Tales in the Thomas Schelling game. We propose a metric according to which only one player will regard the two strategies as identical. We call that player the leader. All (in an n-player example) the other players are free to impose different distance functions on pairs of strategies. So, in our canonical illustration suppose P2 is oriented towards ‘Tails’. P1 will be the leader as she will be indifferent between the two strategies. Since she is indifferent between the two outcomes she may (or may not) flip a coin and decide. Her call would be a coordinating device. P2, the follower, knows that she is not worse off following her lead and changing her orientation if ‘Heads’ is called. The coordination problem is solved.
In this ‘Heads’ and ‘Tails’ game, if both players P1 and P2 concatenate their calls on the same face of a coin they earn a billion dollars each. Otherwise, they earn nothing. How does a reader with a knowledge of elementary game theory approach this problem? Surely, in Nash terms. That is, she will work out the optimal choice of row for P1 for all possible choices of columns of P2, and symmetrically the optimal choice of column for P2 for all possible choices of rows of P1. In the present case, both the diagonal terms are equilibria. Claude Berge, the mathematician, invited the profession to look at the problem in ‘complementary’ terms. Imagine P1 optimizing over columns, given the choices of rows, and P2 optimizing over rows, given the choices of columns. Berge was at the right time at the right place, Princeton in the earlier heyday of game theory. Yet, his ideas were met with less than enthusiasm. Language was partly to blame (not all his French writings are translated) and partly his terse mathematical exposition was not appreciated by economists. It is only in recent years that scholars have evinced interest in his work. On the one hand, mathematicians have refined and extended his results [2]. The agenda was, to some extent, given. For instance, the assumptions of quasi-concavity and upper semicontinuity had to be directed to the product strategy space of the other players j from the strategy set of player i. Greater expectations have been laid on his results by social scientists because a Berge Equilibrium (BE) provides the cooperative outcome in the standard illustrations in which the Nash Equilibrium (NE) does not [3], [4]. The population of social scientists referred to does not include economists and the reason is not far to seek. Why should agent i maximize over the choices of others? Edna Ullman-Margalit offers a minimal requirement in “considerateness” defined as actions designed to decrease the discomfort of others at trivial costs to oneself [5]. The ‘others’ could be anonymous as well as familiar. Gratitude may or may not result but reciprocity is expected. Considerateness can be distinguished from other well-known notions. Thus, ‘altruism’ is the case when the costs and benefits to others are significant. Considerateness is the minimal acknowledgement of the existence of the other qua respect for others as human beings and falls short of ‘kindness’. The expectation is that others are considerate but, at the same time, the considerate act of the agent contributes towards fostering such an environment. In the literature, players are free to play Nash or Berge. The state of the art is one in which both outcomes are possible and a set of theorems connects the two concepts. For instance, the two-player Prisoner’s Dilemma is a special case of the n-person Prisoner’s Dilemma. In both cases, defection is the unique NE and cooperation is the unique BE. The NE represents the individualistic idea within interdependence theory while the BE stands for the social value orientation within that theory. According to what has been called self-construal, individuals are both independent selves and interdependent selves [6]. Prosocial behavior is typically associated with the interdependent self. People imbued with characteristics like benevolence usually expect others to be similarly disposed. Situational triggers will activate one self or the other. In the study referred to, experiments were conducted to show that the selves could be manipulated. In this regard, scholars distinguish between moral sentiments and other-regarding preferences [4]. According to the latter, individual utility functions have two arguments, one concerned with self-welfare, the second with the welfare of others. Both Nash and Berge behavior rules can be rationalized according to this extended definition. The reference to moral sentiments leads to Adam Smith’s Theory of Moral Sentiments from which the evolution from BE to NE and back in historical time can be traced [7]. Till the eighteenth century, the understanding was that individuals recognized their fellow-beings as extensions of themselves. With the onset of the theory of social Darwinism, empathy was substituted by models emphasizing individual fitness which, more often than not, led to suboptimal competitive interactions between people. The end of the last century and the beginning of the present have witnessed a renewed interest in social interactions on foundations other than self-interest. Current thinking in all strains of Darwinist reasoning is cast in terms of the information content of specific instructions in guiding evolution [8-10]. For instance, the influence of the philosopher Herbert Spencer, who coined the term ‘the survival of the fittest’, lingers. However, similar to the case made by the economist-sociologist Thorstein Veblen, he argued that the survival of the fittest required policy interventions. Spencer’s model was moral. His biology was adaptationist, requiring both inheritance as well as acquired characteristics. It is this perspective, rather than social Darwinism, that has stood the test of time. Through sympathy, an agent places herself in the skin of other agents and experiences what she would feel if she was actually in their situations. The movement is instantaneous and triggered by specific circumstances. If the feelings coincide in the particular game, agent i will cooperate with agents j. However, if they do not, agent i will ‘defect’. Sympathy is the basis of moral judgments. Both Nash and Berge norms are internalized.In the NE the rational agent attempts to achieve the best-act profile by choosing only one component of the profile. The BE makes the substitution that it is the best-act profile of the others that the individual deliberates over. What is parametric in NE is choice-theoretic in BE and vice versa. Michael Bacharach and Thomas Schelling worked with the idea that agents choose whole profiles. In terms of our example, it is unnecessary, then, to dwell on P1 and P2. We need to ‘think inside the box’. Between themselves, agents implement their profile choices. If all play their part in the solution vector it will be unique. Bacharach and Schelling pioneered reasoning in one-shot engagements. Attempts to understand Bacharach’s ‘team reasoning’ have run the gamut from philosophy to neuroscience [11]. Players might obey Kant’s categorical imperative: Do unto others as you would have others do unto you [12], [13]. The effectiveness of a strategy depends upon the others who adopt it. Thus, deviation in a prisoner’s dilemma is inconsistent. Players deviate to gain, not to lose. If deviation is universalized, all lose. In other words, the equilibrium does not satisfy Al-Suwalem’s criterion of universalizability. Other criteria offered to distinguish ecological or social rationality from individual rationality include ‘reversibility’. Accordingly, in two-player games actions are chosen which are optimal if each player put herself in the other’s shoes. The axiom is extended to groups by iterating the rule. The ‘reversible rule’ thus becomes universalizable. Neuroscience contributes ‘empathy’. ‘Mirror neurons’ enable a player to identify with others. Feelings and emotions connect spontaneously. It is more costly for the neural system to isolate feelings than to relate to interacting parties. Our brains are hardwired with cooperative mechanisms. A final precept is the axiom of ‘symmetry or invariance under the permutation of individuals’. Players displaying groupthink search for a profile of strategies that maximizes the collective payoffs of the group. That profile need not be a Nash equilibrium. If one payoff Pareto-dominates the others, that payoff clearly maximizes the collective payoff. If the optimizing payoff is unique, members of the team play their component strategies in the profile. If not, the theory is indeterminate.Returning to our motivating example, Bacharach and Schelling were inspired, above all, by the fact of life that people, in general, solve cooperation problems. Complexity is introduced in the ‘Heads’ and ‘Tails’ game by the assumption that ‘Heads’ and ‘Tails’ might resonate differently for P1 and P2. They do not flip an unbiased coin to decide. Yet, Bacharach reports that people, in an overwhelming number of instances, call ‘Heads’. ‘Heads’, he suggests, possesses a different ‘salience’ from ‘Tails’. The experiments and tests could be replicated across cultures and time and space and, it is possible, ‘Tails’ is called out in a majority of those instances. The point remains. The problem is, in general, solved. In sum, the intuition connecting the three scientists in the title of the paper is the cooperative solution in one-shot coordination games. How might we get the northwest solution in the box above? Schelling would have suggestive numbers in that corner. Bacharach would argue that while both players might have different mental frames, one favoring ‘Heads’, the other ‘Tails’, the orientations are flexible. As an illustration of we-thinking they would modify their impulses to arrive at the solution ‘Heads’. Recently, Oded Stark [14] has proposed that in an economics of others, players change off-diagonal elements in the one-shot Prisoner’s Dilemma so as to coordinate on the best outcome. We develop the idea that a mediator is sufficient to lead the way to ‘Heads’. Schelling suggests the possibility of a leader, [15, p.91], Bacharach a director (albeit from outside the game) [16, p.123]. Bacharach offers the notion of myopia by means of which leaders/directors collapse the variable frames of all the players to a point [16, p.86]. The current development of the idea runs independent of the concepts surrounding reward and punishment [17]. Dictators in the famous game that bears that name turn out to be “generous” in reality. Their concern, primarily, is to preserve the pie and maximize social welfare. Mathematically, different ways of seeing a matrix game translates into different metrics players might impose between pairs of strategies. We revisit the Helly metric that underpins the NE. That metric does not enable the players to distinguish between Heads and Tales in the Thomas Schelling game. We propose a metric according to which only one player will regard the two strategies as identical. We call that player the leader. All (in an n-player example) the other players are free to impose different distance functions on pairs of strategies. So, in our canonical illustration suppose P2 is oriented towards ‘Tails’. P1 will be the leader as she will be indifferent between the two strategies. Since she is indifferent between the two outcomes she may (or may not) flip a coin and decide. Her call would be a coordinating device. P2, the follower, knows that she is not worse off following her lead and changing her orientation if ‘Heads’ is called. The coordination problem is solved. 2. On Leadership
- Many others have advised that a leader must emerge from among players in coordination games to bring about a determinate solution. For instance, in an experiment on a one-stage Prisoner’s Dilemma game with a finite strategy space the unique cooperative outcome emerges when players alternate in exerting power to end the game [18]. Again, giving by a pair is higher and more stable when one of the two is a leader [19]. Yet again, in the first natural field experiment on the dictator game where subjects are unaware that they are participating in an experiment, the outcomes turn out counter to the standard results [20]. Dictators display a large measure of pro-social behavior. A step towards that end is the notion of a mediator who operates from a contractarian perspective [21]. A mediator shows individuals how they can dovetail their actions to mutual benefit. The proposition runs as follows: It is in the interest of each separately to agree to perform the act together. The plan is not a set of mutually consistent instructions sent to each player separately but is a unique recommendation addressed to the collection of individuals. A key facet of contractarian reasoning is that it favors general rules rather than particular solutions. For instance, the notion of leadership recommended below does not deliver the same leader in all situations. Each player will not benefit identically from every application of the rule considered independently. Rather, each will benefit overall from the general application of the rule. No incentives are called for. Leaders must be able to do no more than convey unambiguous signals [22]. As an example, using material from standard psychology tests, Laurence M Ball argues that groupthink is at work at the Federal Open Markets Committee (FOMC) [23]. There is a regular tendency for members to accept a perceived majority view rather than express their personal preferences. The reason is that they value group harmony. One route to this end is the existence of a “directive leader”. Professor Ball observes that it is not obvious that Ben Bernanke played that role, paradoxically, even when he became Governor of the Federal Reserve. Team reasoning is absent in the deliberations of the Bank of England’s Monetary Policy Committee. Each member of the committee is legally enjoined to vote based on an individual preference function. There is no directive leader nor a desire to seek consensus. Five-four votes on policy decisions are not uncommon and the Governor is as likely to be on the side of the minority as the other.
3. A Suitable Metric
- We have noted that there are at least three different ways to view a game, the familiar Nash, the unfamiliar Berge, and the quasi-unfamiliar Bacharach-Schelling. Formally, disparate ways of seeing translates into different metrics that could be imposed on the game. We proceed to excavate the Helly metric that underpins the Nash and Berge definition of equilibrium. To that end, consider the following game G in normal form,
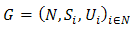 where N is the set of players, Si the set of strategies of player i,
where N is the set of players, Si the set of strategies of player i, 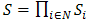 is the set of situations of the game G,
is the set of situations of the game G, 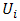 :
: 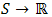 is the payoff function of player i. The individual strategy spaces are assumed to be compact and, consequently, the product space is compact. In the usual way,
is the payoff function of player i. The individual strategy spaces are assumed to be compact and, consequently, the product space is compact. In the usual way, 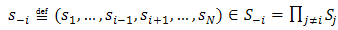 . We have the NE given byDefinition 1.
. We have the NE given byDefinition 1. 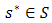 is said to be a NE if
is said to be a NE if 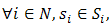
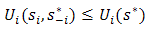 The NE is immune to unilateral deviations. Given that all players j play their Nash strategy, player i has no incentive to deviate from her Nash strategy. Less familiar is the BE: Definition 2.
The NE is immune to unilateral deviations. Given that all players j play their Nash strategy, player i has no incentive to deviate from her Nash strategy. Less familiar is the BE: Definition 2.  is said to be a BE if
is said to be a BE if 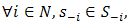
 The maximization of player i’s utility is carried out over the strategy sets of the other players j. Player i maximizes her utility when all the other players j play their Berge strategies. When the other players deviate, player i is worse off and she is not necessarily better off by deviating herself. However, in BE all players j maximize the utility of i and the others. In many games, everyone is better off. This is mutual support.We have pointed out aspects of the mathematical research programme. For the proof of the existence of NE,
The maximization of player i’s utility is carried out over the strategy sets of the other players j. Player i maximizes her utility when all the other players j play their Berge strategies. When the other players deviate, player i is worse off and she is not necessarily better off by deviating herself. However, in BE all players j maximize the utility of i and the others. In many games, everyone is better off. This is mutual support.We have pointed out aspects of the mathematical research programme. For the proof of the existence of NE, 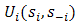 must be quasi-concave in
must be quasi-concave in 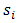 for all
for all 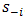 . Along identical lines, for the application of fixed-point theorems to prove the existence of BE,
. Along identical lines, for the application of fixed-point theorems to prove the existence of BE, 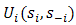 must be quasi-concave in
must be quasi-concave in 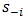 for all
for all 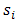 . The assumption of upper semicontinuity in the case of Nash translates in similar fashion to the case of Berge. We move from one component of strategy profiles (NE) to N – 1 vectors (BE) to complete strategy profiles (Bacharach-Schelling). Consequently, we make the following assumption: Assumption: We assume that the payoff functions
. The assumption of upper semicontinuity in the case of Nash translates in similar fashion to the case of Berge. We move from one component of strategy profiles (NE) to N – 1 vectors (BE) to complete strategy profiles (Bacharach-Schelling). Consequently, we make the following assumption: Assumption: We assume that the payoff functions 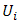 are upper semicontinuous on S. We define the upper semicontinuity of the function
are upper semicontinuous on S. We define the upper semicontinuity of the function 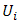 on S as follows with η the radius of neighborhood
on S as follows with η the radius of neighborhood 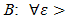
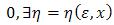 such that
such that 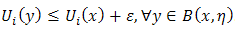 .Underlying the Nash equilibrium is the Helly metric [24], [25]:Definition 3. For any two strategies
.Underlying the Nash equilibrium is the Helly metric [24], [25]:Definition 3. For any two strategies 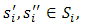
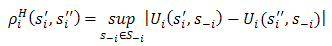 The connection with the NE of Definition 1 can perhaps be more clearly seen if we write the right-hand side of the equation as
The connection with the NE of Definition 1 can perhaps be more clearly seen if we write the right-hand side of the equation as 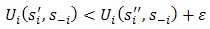 Note that the metric does not satisfy the ‘separation of points’ criterion of a metric and, hence, is often called a pseudometric. When the use of two different strategies by player i leads to the same payoffs, the two strategies are to be regarded as identical. Formally put,
Note that the metric does not satisfy the ‘separation of points’ criterion of a metric and, hence, is often called a pseudometric. When the use of two different strategies by player i leads to the same payoffs, the two strategies are to be regarded as identical. Formally put, 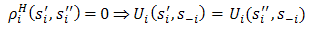 Over all players j, we arrive at the conclusion that for all players j ∈ N,
Over all players j, we arrive at the conclusion that for all players j ∈ N, 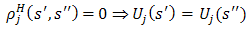 Clearly, the so-called pseudometric also underlies the Berge equilibrium:Definition 3′. For any two strategies
Clearly, the so-called pseudometric also underlies the Berge equilibrium:Definition 3′. For any two strategies 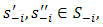
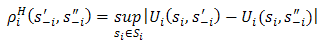 If two N–1 different strategy profiles lead to the same payoffs for player i, they are to be regarded as identical. Extending the metric to the Bacharach-Schelling case where the components of strategies are not of concern, we observe that the metric would be of interest if two strategies are not ‘close’. Let us, in that case, consider two strategies
If two N–1 different strategy profiles lead to the same payoffs for player i, they are to be regarded as identical. Extending the metric to the Bacharach-Schelling case where the components of strategies are not of concern, we observe that the metric would be of interest if two strategies are not ‘close’. Let us, in that case, consider two strategies 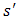 and
and 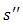 that belong to different neighborhoods as given in our assumption/definition of upper semicontinuity. Denote the epigraph of the function
that belong to different neighborhoods as given in our assumption/definition of upper semicontinuity. Denote the epigraph of the function 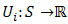 by the subset
by the subset 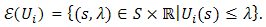 We know that the upper semicontinuity of the function
We know that the upper semicontinuity of the function  on S is equivalent to the property that the epigraph of the function
on S is equivalent to the property that the epigraph of the function 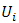 is closed. In the case of strategies that are ‘far enough apart’ we haveProposition 1. The Helly pseudometric is a metric.Proof. Let
is closed. In the case of strategies that are ‘far enough apart’ we haveProposition 1. The Helly pseudometric is a metric.Proof. Let 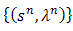 be a sequence of points of
be a sequence of points of 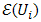 that converge to
that converge to 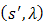 . Now,
. Now, 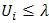 . If
. If 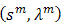 is a sequence of points that converges to
is a sequence of points that converges to 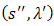 , then
, then 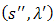
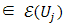 for some
for some 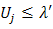 . That is to say, if
. That is to say, if 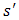 is not close to
is not close to 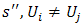 .In other words,
.In other words, 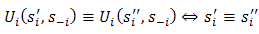 . ‘Heads’ and ‘Tails’ are different. Indeed, they are each closed sets. Thus, we are no closer to solving our problem and rationalizing the choice of ‘Heads’. Under the Helly metric, people regard ‘Heads’ and ‘Tails’ as indistinguishable. They would flip a coin to decide. On the other hand, the proposition reflects our earlier discussion that ‘Heads’ and ‘Tails’ means different things to different people. Thus, if it is reasonable to assume that half of the N players are predisposed to calling ‘Heads’ and half are predisposed to calling ‘Tails’ we do not solve the problem in a single foray.For the purpose we propose the Bacharach-Schelling (BS) metric:Definition 4. For any two strategy profiles
. ‘Heads’ and ‘Tails’ are different. Indeed, they are each closed sets. Thus, we are no closer to solving our problem and rationalizing the choice of ‘Heads’. Under the Helly metric, people regard ‘Heads’ and ‘Tails’ as indistinguishable. They would flip a coin to decide. On the other hand, the proposition reflects our earlier discussion that ‘Heads’ and ‘Tails’ means different things to different people. Thus, if it is reasonable to assume that half of the N players are predisposed to calling ‘Heads’ and half are predisposed to calling ‘Tails’ we do not solve the problem in a single foray.For the purpose we propose the Bacharach-Schelling (BS) metric:Definition 4. For any two strategy profiles 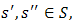
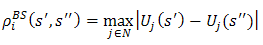 Once more, the right-hand side can be expressed as
Once more, the right-hand side can be expressed as 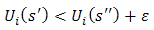 Given the two strategy profiles, the maximization operation is carried out over the metrics of all players j to determine the metric of player i. Naturally, the familiar metric on the real number line will be the outcome although we use the same symbol to denote the different distance functions players may impose on the game. Recall the intuition that the metric is the shortest distance between two points. Going over all strategy pairs we arrive at the outcome that is at most a distance epsilon from the other outcomes. The illustration below and the ones following are drawn from [3].
Given the two strategy profiles, the maximization operation is carried out over the metrics of all players j to determine the metric of player i. Naturally, the familiar metric on the real number line will be the outcome although we use the same symbol to denote the different distance functions players may impose on the game. Recall the intuition that the metric is the shortest distance between two points. Going over all strategy pairs we arrive at the outcome that is at most a distance epsilon from the other outcomes. The illustration below and the ones following are drawn from [3]. Here both the NE and the BE coincide off the main diagonal. The BS metric would work as follows: We conjecture that the metric leads us to (C1,C2). Dropping the absolute value symbol, work out the distance between that payoff and the other payoffs. Thus, (2,2) – (4,3) = (2,1); (2,2) – (1,1) = (1,1). The other candidates give a ‘longer’ distance between points. For instance, (4,3) – (1,1) = (3,2). The solution meets Schelling’s criterion of a focal point. It should be noted that (D1, D2) meets the requirement as well. We can motivate this outcome by the imposition of the minimum operator instead of the maximum operator in our definition. Since there is no player performing the operation, minimization of payoffs is not perverse. Indeed, economists will find Berge more congenial if his axiom is that players minimize the payoffs of others. Only, in that case, the outcomes in the Thomas Schelling game are the null payoffs off the main diagonal. When individuals’ mental frames differ or, indeed, they are prone to self-destructive behavior, a leader can influence outcomes by manipulating frames. For instance, it is possible that players will not settle on anything less than the maximum of their individual payoffs independent of the choices of others. Most games would not have a solution in that case. The ‘choice architect’ does not impose her choices on the others but does no more than enable them to realize their potentials in an agenda called “soft paternalism” [26]. Simply put, the BS metric delivers the vector with the ‘highest’ payoffs, at most a distance epsilon away from the next best solution vector. The separation of
Here both the NE and the BE coincide off the main diagonal. The BS metric would work as follows: We conjecture that the metric leads us to (C1,C2). Dropping the absolute value symbol, work out the distance between that payoff and the other payoffs. Thus, (2,2) – (4,3) = (2,1); (2,2) – (1,1) = (1,1). The other candidates give a ‘longer’ distance between points. For instance, (4,3) – (1,1) = (3,2). The solution meets Schelling’s criterion of a focal point. It should be noted that (D1, D2) meets the requirement as well. We can motivate this outcome by the imposition of the minimum operator instead of the maximum operator in our definition. Since there is no player performing the operation, minimization of payoffs is not perverse. Indeed, economists will find Berge more congenial if his axiom is that players minimize the payoffs of others. Only, in that case, the outcomes in the Thomas Schelling game are the null payoffs off the main diagonal. When individuals’ mental frames differ or, indeed, they are prone to self-destructive behavior, a leader can influence outcomes by manipulating frames. For instance, it is possible that players will not settle on anything less than the maximum of their individual payoffs independent of the choices of others. Most games would not have a solution in that case. The ‘choice architect’ does not impose her choices on the others but does no more than enable them to realize their potentials in an agenda called “soft paternalism” [26]. Simply put, the BS metric delivers the vector with the ‘highest’ payoffs, at most a distance epsilon away from the next best solution vector. The separation of 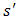 and
and 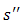 requirement of a metric is met for all players j except player i. Thus, all players other than i will distinguish between strategies
requirement of a metric is met for all players j except player i. Thus, all players other than i will distinguish between strategies 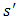 and
and 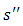 even if they offer the same payoffs. Only i will regard them as identical. She would be indifferent between the two strategies. In symbols,
even if they offer the same payoffs. Only i will regard them as identical. She would be indifferent between the two strategies. In symbols,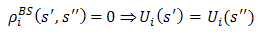 The expression looks similar to the earlier concerning the Helly metric but this property only applies to player i. On the last occasion it applied to all the players. We call i the leader because she is an individual picked by the maximization of utilities operation carried out over all the players. It can easily be seen that the metric
The expression looks similar to the earlier concerning the Helly metric but this property only applies to player i. On the last occasion it applied to all the players. We call i the leader because she is an individual picked by the maximization of utilities operation carried out over all the players. It can easily be seen that the metric 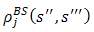 over
over 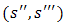 given by another leader j generates a metric
given by another leader j generates a metric 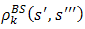 and a leader k over a strategy pair
and a leader k over a strategy pair 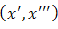 . In other words, the ‘triangle inequality’ is satisfied. The metric applies to all other strategy pairs and potential leaders. In effect, the problem of the multiplicity of equilibria is solved by transforming the problem into individual choice exercises. The notion of leadership, in contrast to other notions like “practical authority”, is concerned with the task on hand and lasts only for the duration of the job [27], [28]. People follow the leader only because everyone is following her and only to the extent that the metric serves the purpose of coordination, not because it is the metric of the leader. Neither formal authority nor personal or contextual traits are necessary. Leaders are able to align and commit actions by participating in the procedure themselves. They are average group members. In game 1a below we have a representation of the “Chicken” or “Hawk-Dove” game. The BE at (C1,C2) meets the requirement of the BS metric and is unique. Its symmetry also meets Schelling’s requirement of the salience and prominence of a focal point. The NE are (D1,C2) and (C1,D2). In game 1b, it is the unique NE at (C1,C2) that meets the requirement of the BS metric (and a focal point). Here, there are multiple BE at (C1,D2) and (D1,C2). In case 1a, we have (3,3) – (2,4) = (1,1); (3,3) – (1,1) = (2,2) whereas both (4,2) and (1,1) are inferior as candidates since (4,2) – (1,1) = (3,1). (2,2) is ‘smaller’ than (3,1).
. In other words, the ‘triangle inequality’ is satisfied. The metric applies to all other strategy pairs and potential leaders. In effect, the problem of the multiplicity of equilibria is solved by transforming the problem into individual choice exercises. The notion of leadership, in contrast to other notions like “practical authority”, is concerned with the task on hand and lasts only for the duration of the job [27], [28]. People follow the leader only because everyone is following her and only to the extent that the metric serves the purpose of coordination, not because it is the metric of the leader. Neither formal authority nor personal or contextual traits are necessary. Leaders are able to align and commit actions by participating in the procedure themselves. They are average group members. In game 1a below we have a representation of the “Chicken” or “Hawk-Dove” game. The BE at (C1,C2) meets the requirement of the BS metric and is unique. Its symmetry also meets Schelling’s requirement of the salience and prominence of a focal point. The NE are (D1,C2) and (C1,D2). In game 1b, it is the unique NE at (C1,C2) that meets the requirement of the BS metric (and a focal point). Here, there are multiple BE at (C1,D2) and (D1,C2). In case 1a, we have (3,3) – (2,4) = (1,1); (3,3) – (1,1) = (2,2) whereas both (4,2) and (1,1) are inferior as candidates since (4,2) – (1,1) = (3,1). (2,2) is ‘smaller’ than (3,1). 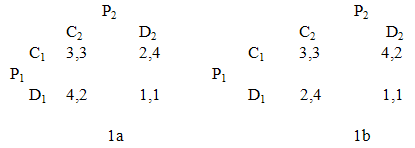 Game 2a below has a unique NE at (C1,C2) and a unique BE at (D1,D2) while the transformation 2b is the Prisoner’s Dilemma with a unique NE at (D1,D2) and a unique BE at (C1,C2). In both cases, the BS metric leads to the outcome (3,3). Here, however, (D1,D2) meets the requirements of the BS metric as well. In the earlier examples, the max operator has not been deployed because the equilibria were unique. In the present instance, maximization leads to (C1,C2).
Game 2a below has a unique NE at (C1,C2) and a unique BE at (D1,D2) while the transformation 2b is the Prisoner’s Dilemma with a unique NE at (D1,D2) and a unique BE at (C1,C2). In both cases, the BS metric leads to the outcome (3,3). Here, however, (D1,D2) meets the requirements of the BS metric as well. In the earlier examples, the max operator has not been deployed because the equilibria were unique. In the present instance, maximization leads to (C1,C2). 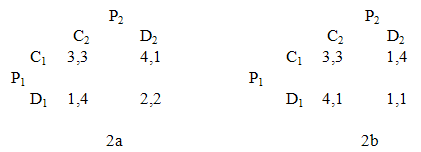 In experiments, the frequency of Pareto-dominant actions increases among leaders in the Prisoner’s Dilemma and the stag-hunt game if the actions block the potential payoffs of followers from decreasing [29]. A significant increase in the coordinating action under both positive and negative externalities illustrates that global welfare-improving action is supported as equilibrium action in the stage game. An attractive property of a metric space is that it fulfill the Cauchy criterion. That is, any given sequence of points converges. We confirm the following: Proposition 2. The Bacharach-Schelling metric space is complete.Proof. We know that ℝ is complete and denote the Euclidean metric by
In experiments, the frequency of Pareto-dominant actions increases among leaders in the Prisoner’s Dilemma and the stag-hunt game if the actions block the potential payoffs of followers from decreasing [29]. A significant increase in the coordinating action under both positive and negative externalities illustrates that global welfare-improving action is supported as equilibrium action in the stage game. An attractive property of a metric space is that it fulfill the Cauchy criterion. That is, any given sequence of points converges. We confirm the following: Proposition 2. The Bacharach-Schelling metric space is complete.Proof. We know that ℝ is complete and denote the Euclidean metric by 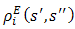 .Let
.Let  be a sequence of elements
be a sequence of elements  If
If 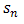 converges to s, then
converges to s, then 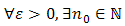 such that
such that 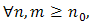
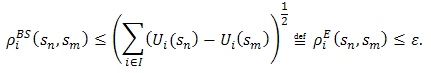
4. Conclusions
- The Nash equilibrium concept has the well-known limitation of being unable to explain cooperation in a large variety of noncooperative contexts. Strangers come together, never to meet again, and cooperate. The contribution of Berge is to direct attention to the ‘others’ without deflecting attention away from the individual who is the subject of analysis. While players maximize their payoff functions, the domain is the product strategy space of all the other players. We highlight the Helly metric underpinning both solution concepts. Rather than distinguishing between the ‘self’ and the ‘others’, Michael Bacharach and Thomas Schelling were concerned with the space of situations. We propose a measure to capture their insights. Coordination games contain multiple equilibria. Yet, people in the ordinary business of life routinely solve them to mutual benefit. Among many avenues, they suggested that a leader is required to pick a solution. Our metric suggests a leader in a large class of well-known games. In the case of a tie, while some players will prefer to call ‘Heads’ and the others ‘Tails’ in the ‘Heads’ and ‘Tails’ game and, thereby, not solve the pure coordination problem, the leader would be indifferent and suggest one arbitrarily. The others would have no reason not to play their part in the plan.
ACKNOWLEDGEMENTS
- The comments and appraisal of an anonymous referee are gratefully acknowledged. I retain, however, complete responsibility for any errors that may remain.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML