Journal of Game Theory

p-ISSN: 2325-0046    e-ISSN: 2325-0054

2015;  4(1): 1-5

doi:10.5923/j.jgt.20150401.01

On the Evolution of Cooperative Behavior in Prisoner’s Dilemma

Essam El Seidy, Ali M. Almuntaser

Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt

Correspondence to: Ali M. Almuntaser, Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt.

Email:

Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.

Abstract

Cooperation is always vulnerable to exploitation by defectors in the prisoner's dilemma game unless a mechanism for the evolution of cooperation is at work. Hence, the evolution of cooperation requires specific mechanisms, which allow natural selection to favor cooperation over defection. There are some mechanisms like kin selection, group selection, direct and indirect reciprocity can evolve the cooperation when it works alone. Here we combine two and three mechanisms together in one population. The transformed matrices for each combination are determined. We show that, when two or three mechanisms works together, a strong cooperation can evolve between players more than when each mechanism works alone. Some properties of cooperation like risk-dominant (RD) and advantageous (AD) are studied. The property of evolutionary stable (ESS) for strategies which used in this paper is discussed.

Keywords: Prisoner’s Dilemma, Evolutionary game dynamics, Evolution of cooperation, Direct and Indirect reciprocity, Group selection, Kin selection

Cite this paper: Essam El Seidy, Ali M. Almuntaser, On the Evolution of Cooperative Behavior in Prisoner’s Dilemma, Journal of Game Theory, Vol. 4 No. 1, 2015, pp. 1-5. doi: 10.5923/j.jgt.20150401.01.

Article Outline

1. Introduction
2. Evolutionary Game Dynamics
    2.1. Kinselection in Prisoner’s Dilemma (PD)
    2.2. Direct Reciprocity with Kin Selection
    2.3. Indirect Reciprocity with Kin Selection
    2.4. Group Selection with Kin Selection in PD Game
    2.5. Direct and Indirect Reciprocity with Kin Selection in PD Game
3. Conclusions

1. Introduction

The behavior of strategies especially for the cooperative behavior become a dilemma. This dilemma arises when two cooperators receive a higher payoff than two defectors (Hauert, Michor, Nowak and Doebeli, 2006; Nowak, 2012). The iterated Prisoner's Dilemma has become the paradigm for the evolution of cooperation among egoists. Since Axelrod's classic computer tournaments and Nowak and Sigmund's extensive simulations of evolution, we know that natural selection can favor cooperative strategies in the Prisoner's Dilemma. The Iterated Prisoner's Dilemma (IPD) is now regarded as an ideal experimental platform for the evolution of cooperative behavior; it is the strongest form of a cooperative dilemma where cooperation requires a mechanism for evolution. A mechanism is an interaction structure that specifies how players in the population interact to receive payoff and how they compete (Nowak, 2006).
In the prisoner’s dilemma (PD) two players have two behavioral options, either to cooperate (C) or to defect (D). After choosing strategies, payoff of each player is decided by the following payoff matrix:
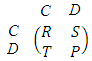In this matrix, the meaning of every capitalized letter is follows; T - Temptation to defect, R - Reward for mutual cooperation, P – Punishment and S - Sucker's payoff. In the prisoner's dilemma game, the condition T > R > P > S is necessary, and for the iterated prisoner's dilemma game, the additional condition 2R>T+S should be satisfied.
In the Prisoner's Dilemma, defectors dominate cooperators unless a mechanism for the evolution of cooperation is at work and cooperation is always vulnerable to exploitation by defectors. Hence, the evolution of cooperation requires specific mechanisms, which allow natural selection to favor cooperation over defection.
In Nowak and Taylor (2007), they studied five mechanisms for evolution of the cooperative behavior, direct and indirect reciprocity, kin selection, group selection, and network reciprocity these mechanisms have been proposed to explain the evolution of cooperative behavior. The kinselection focuses on cooperation among individuals who are closely related genetically (Nowak 2006a), whereas directreciprocity focus on the selfish incentives for cooperation in repeated interactions (Axelrod, 2006). The indirectreciprocity show how cooperation in larger groups can emerge when the cooperators can build a reputation, Networkreciprocity operates in structured populations, where cooperators can prevail over defectors by forming clusters (Nowak and Taylor, 2007). They studied each mechanism separately and they found the transformed matrices for each mechanism. They derived the necessary condition for evolution of cooperation and evolutionary stability property of strategies. Here we complete them work and study the evolution of the cooperative behavior by combine two or three mechanisms together and find the transformed matrices for each situations. We derive the conditions for the evolution of cooperative behavior and study the (ESS) property of the strategies that we will use it in our study. Also we derive the necessary conditions that make the cooperation risk- dominant and advantageous in a population.
All combinations of the mechanisms that we will combine it together lead to different mathematical investigations. In this paper we study this mechanisms in the context of the Prisoner's Dilemma (PD) game.
At first, we introduce simple remarks on evolutionary games dynamics. Then we discuss the evolution of cooperative behavior when we combine two or more mechanisms together.

2. Evolutionary Game Dynamics

Evolutionary game theory differs from classical game theory by focusing more on the dynamics of strategy change as influenced not solely by the quality of the various competing strategies, but by the effect of the frequency with which those various competing strategies are found in the population. Evolutionary game theory has proven itself to be invaluable in helping to explain many complex and challenging aspects of biology. It has become of increasing interest to economists, sociologists, anthropologists, and philosophers (Hofbauer and Sigmund 2003; El Seidy 2003; Nowak and Sigmund 2004; El-Seidy and Arafat 2013).
Now consider a game between two strategies, A and B. If two A players interact, both get payoff a; if A interacts with B, then A gets b and B gets c; if two B players interact, both get d. These interactions are represented by the following payoff matrix:
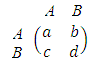Now:
1. If a > c and b > d, then A dominates B. In this case, it is always better to use strategy A. The expected payoff of A players is greater than that of B players for any composition of a well-mixed population. If instead a < c and b < d, then B dominates A, and we have exactly the reverse situation.
2. If a > c and b < d, then both strategies are best replies to themselves, which leads to a “coordination game.” In a population in which most players use A, it is best to use A. In a population in which most players use B, it is best to use B. a coordination game leads to bi-stability: both strategies are stable against invasion by the other strategy (Taylor and Nowak 2007).
3. If a < c and b > d, then both strategies are best replies to each other, which leads to a “Hawk–Dove game” (Maynard Smith 1982). In a population in which most players use A, it is best to use B. In a population where most players use B, it is best to use A. (Nowak, Tarnita and Antal 2010).
4. If a >c then A is a strict Nash equilibrium. Likewise, if b then B is a strict Nash equilibrium. The strategy that is a strict Nash equilibrium is always an evolutionarily stable strategy (ESS) (Taylor and Nowak 2007).
5. If a + b > c + d then A is risk-dominant (RD). If both strategies are ESS, then the risk-dominant strategy has the bigger basin of attraction.
6. If a + 2b > c + 2d then A is advantageous (AD). This concept is important to stochastic game dynamics in finite populations (Antal, Nowak, and Traulsen 2009; Nowak 2006b; Nowak, Tarnita and Antal 2010).

2.1. Kinselection in Prisoner’s Dilemma (PD)

A simple way to study games between relatives was proposed by Maynard Smith for the Hawk-Dove game (Maynard Smith 1982). Consider a population where the average relatedness between individuals is given by r, which is a number between 0 and 1 (see Doebeli, Hauert 2005; Nowak, 2006b). We will assume that the payoff received by a relative is multiplied by r and added to my own payoff. Therefore, using P.D game we obtain the modified matrix:
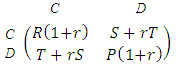From this transformed matrix, we get the following outcomes:
1. The strategy of cooperation will be ESS (evolutionary stable strategy), if E(C,C)>E(D,C) i.e. when .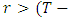
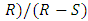2. Cooperators can invade a population of defectors if E(C,D>(D,D), i.e. when .
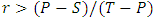3. The cooperation will be risk-dominant (RD) whenever E(C,C)+E(C,D)>E(D,C)+E(D,D), i.e. when .
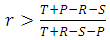4. Also cooperation will be advantageous (AD) if E(C,C)+2E(C,D)>E(D,C)+2E(D,D), i.e. when .
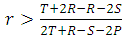Where E(C,C), for example, is the payoff value of first player who plays with strategy C against the second player who plays with strategy C.

2.2. Direct Reciprocity with Kin Selection

Direct reciprocity is considered to be a powerful mechanism for the evolution of cooperation, and it is generally assumed that it can lead to high levels of cooperation. Direct reciprocity has been studied by many authors (Axelrod, 2006; Nowak 2006a). This mechanism can emerge in repeated games and lead to the evolution of cooperative behavior. It is based on the concept that “I help you and you help me”. In each round the two players must choose to cooperate or to defect with probability w there is another round.
Taylor and Nowak (2007) showed that defectors are always ESS. Cooperators are ESS if 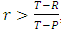, where r is the relatedness degree between players. We will now consider that individuals use direct reciprocity with their relatives. One of the simplest strategies of direct reciprocity is Tit-For-Tat (TFT) where the player cooperates in the first move and then repeats the same opponent’s previous move. We will consider that all the cooperators are using TFT strategy while the defectors are using ALLD. Using the PD game the payoff matrix is given by
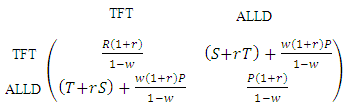From this transformed matrix we can derive the necessary conditions for evolution of cooperative behavior between the strategy TFT and the strategy ALLD. Thus, we get the following conditions:
1. TFT will be stable against defectors if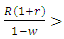 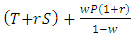, i.e. when .
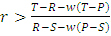2. The population of TFT players invade a population of defectors whenever E(TFT,ALLD)>E(ALLD,ALLD), i.e. when .
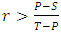3. Cooperation will be risk-dominant if E(TFT,TFT)+E(TFT,ALLD)>E(ALLD,TFT)+E(ALLD,ALLD)i.e. when
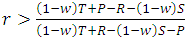4. Cooperation will be advantageous (AD) if E(TFT,TFT)+E(TFT,ALLD)>E(ALLD,TFT)+E(ALLD,ALLD)i.e. when .
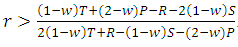From these conditions, we notice that if the two players meet each other again, then the cooperative behavior can evolve even when the relatedness between them is low.

2.3. Indirect Reciprocity with Kin Selection

Indirect reciprocity represents the concept “I help you and somebody will help me.” Indirect reciprocity is a form of reciprocity where cooperators build reputation and trying to cooperate only with the reputed cooperators. This type of reciprocity does not depend upon the probability of meeting the same player again , but it works only if there are players who can distinguishes between the cooperators and defectors (Nowak 2006b ; Leimar and Hammerstein, 2001; Brandt and Sigmund, 2006; Berger, 2011).
To study this situation, we consider that all the cooperators players use distinguish strategy (DIS) and the defectors use ALLD. Let α be the probability that a cooperators players can distinguish between the players who have good or bad reputation, (0 ≤ α ≤ 1). Cooperators will cooperate with the defectors with probability 1- α and the gains and losses of both the individuals will be shared with each other proportional to the average relatedness r between them. Thus, using the PD game, the payoff matrix is given by:
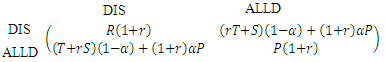Taylor and Nowak showed that, when the indirect reciprocity works alone, then cooperators are (ESS) if α exceed (T-R)/(T-P) and then indirect reciprocity can lead to the evolution of cooperation. If the indirect reciprocity works together with kin selection, then this leads to the following:
1. The cooperators will be stable in the population if E(DIS,DIS)>E(ALLD,DIS), therefore R(1+r)> (T+rS)(1-α)+(1+r)αP, i.e. when 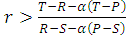. Thus, if the probability of distinguish is more, cooperation can be maintained through indirect reciprocity even when relatedness is low.
2. Cooperators can invade a population of defectors if: E(DIS,ALLD)>E(ALLD,ALLD), thus, (S +r T)(1-α) +(1+r)αP>P(1+r),i.e. when .
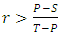3. Cooperation will be risk-dominant (RD) if: E(DIS,DIS)+E(DIS,ALLD)>E(ALLD,DIS)+E(ALLD,ALLD), i.e. when
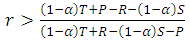4. Cooperation will be advantageous (AD) if: E(DIS,DIS)+2E(DIS,ALLD)>E(ALLD,DIS)+2E(ALLD, ALLD), i.e. when .

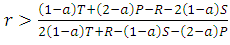2.4. Group Selection with Kin Selection in PD Game

Group selection is based on the idea that competition occurs not only between individuals but also between groups. Group selection has been studied by many authors (see Maynard Smith 1964; Traulsen and Nowak, 2006a). A simple model of group selection works as follows: Consider a population which is subdivided into m groups. The maximum size of a group is n. players in the same group interact with each other through Prisoner’s Dilemma game. Between groups there is no game dynamical interaction, cooperator groups have a constant payoff R, while defector groups have a constant payoff P. in Taylor and Nowak (2007), the necessary condition for evolution of cooperative behavior when group selection works alone is 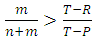, and the defectors are (ESS) if 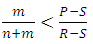We will now consider that there is a relationship between players in the same group, using the PD, and then the payoff matrix is given by
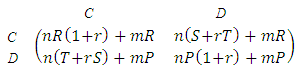From this transformed matrix we get the following conditions:
1. The cooperators will be stable if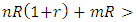 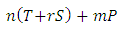, i.e. when 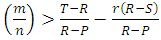. This inequality show that when the relatedness between individuals increases the threshold value of 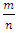will decrease, indicating that kin selection can evolve cooperation within groups when groups are large and the number of groups is small. Thus, group selection works better with kin selection than alone for interacting individuals with any r> 0. The threshold value of relatedness required in the presence of both kin selection and group selection is 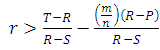, that is mean, kin selection works well in the presence of group selection than alone. Therefore, group and kinselection together can evolve strong cooperation than either of them working alone, especially when average relatedness is low, groups are large and the number of groups is small.
2. The cooperators can be invade a defectors if E(C,D)>E(D,D), if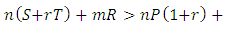 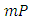, i.e. when .
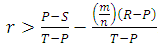3. The cooperation between relatives in the same group will be (RD) if the inequality E(C,C)+E(C,D)>E(D,C)+E(D,D) hold, i.e. when .
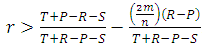4. The cooperation will be (AD) if: E(C,C)+2E(C,D)>E(D,C)+2E(D,D)i.e. when .

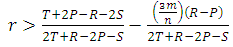2.5. Direct and Indirect Reciprocity with Kin Selection in PD Game

We know that the cooperators who use the strategy TFT will cooperates in the first round, in this situation this strategy can be invasion, here we assume that the TFT’ players can distinguish the players who will be fares against if he has a good or bad reputation. In this case, TFT can avoid the invasion even in the first round, we can thus merge direct and indirect reciprocity and come up with a strategy which will distinguish and cooperate with only cooperators. Thus the payoff matrix of TFT and ALLD strategies using P.D game is given by:
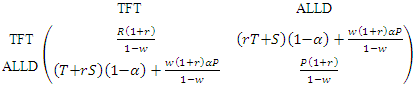where r is the relatedness degree between players and α the probability that a cooperators players can distinguish between the players who have good or bad reputation, and w is the probability that there is another round. When we combine direct and indirect reciprocity with kin selection, we get the following outcomes:
1. The strategy TFT will be ESS if E(TFT,TFT)>E(ALLD,TFT), which leads to 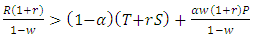, i.e. when 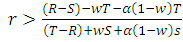. If this inequality holds, then the cooperative behavior can be evolve between players in a population.
2. The cooperators can invade the population of defectors whenever E(TFT,ALLD)>E(ALLD,ALLD), Therefore 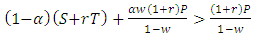, i.e. when .
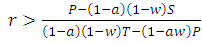3. Cooperation will be risk-dominant (RD) if E(TFT,TFT)+E(TFT,ALLD)>E(ALLD,TFT)+E(ALLD,ALLD),i.e. when
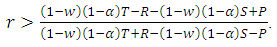4. The Cooperative behavior will be advantageous (AD) whenever E(TFT,TFT)+E(TFT,ALLD)>E(ALLD,TFT) +E(ALLD,ALLD), i.e. whenever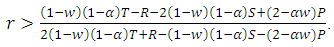

3. Conclusions

In this paper we have studied the evolution of cooperative behavior in context of prisoner’s dilemma P.D game. we have combined more than one mechanism in one population. Each mechanism and any combination of these mechanisms leads to a transformation of the Prisoner’s Dilemma payoff matrix. We determined the transformed matrix for each combination. From transformed matrices, we have derived the necessary conditions for the evolution of cooperative behavior, the conditions which allowed the cooperators to invade the population of defectors, and the conditions that make the cooperation risk- dominant and advantageous. We showed that, in all combinations, when we combine more than one mechanism for evolution of cooperative behavior in one population, then this behavior can evolve more than if each mechanism works alone.
Direct reciprocity can leads to the evolution of cooperative behavior but if it works together with kin selection it can leads to a strong cooperation between players. We found that, the necessary condition for evolution of cooperative behavior is 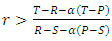, And the population of cooperators can invade a population of defectors if 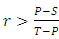. Where r is the average relatedness between individuals, which is a number between 0 and 1, and w is the probability of next round.
Indirect reciprocity also can lead to the evolution of cooperative behavior if it works alone but if we combine it with kin selection , then a strong cooperation in a population can emerge and evolve if the following inequality holds 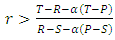, And the population of cooperators can invade a population of defectors if .
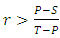When the group selection works with kin selection, then our fundamental conditions, that we derived, showed that cooperation can be maintained in the population even when the average relatedness is low and groups are large. The cooperation can lead to evolution of cooperative behaviour if 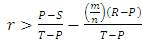. And the population of cooperators can invade a population of defectors whenever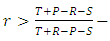 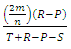. Cooperation will be risk-dominant (RD) whenever 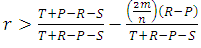. And cooperation will be advantageous (AD) if
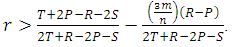Finally, when we combine direct and Indirect reciprocity with kin selection, the strategy Tit-For-Tat (TFT) can avoid the invasion by defectors even in the first round and therefore the cooperative behavior can evolve stronger than if each mechanism works alone. This combination can leads to evolution of cooperative behavior whenever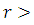 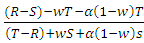. And the population of cooperators can invade a population of defectors if 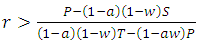. Where r is the relatedness degree between players and α the probability that a cooperators players can distinguish between the players who have good or bad reputation, and w is the probability that there is another round. Also we derived the necessary condition for risk-dominant and advantageous property of cooperation for each combination that we studied.

References

[1]  Antal, T., Nowak, M.A, Traulsen, A. (2009), Strategy abundance in 2 × 2 games for arbitrary mutation rates. J Theor Biol. 2009 March 21; 257(2): 340–344.
[2]  Axelrod, R. (2006), the Evolution of Cooperation, Basic Books, New York.
[3]  Berger, U. (2011), Learning to cooperate via indirect reciprocity. Games and Economic Behavior. 72 (1), 30–37.
[4]  Brandt, H, Sigmund, K. (2006), The good, the bad and the discriminator errors in direct and Indirect reciprocity.J.Theor.Biol.239, 183–194.
[5]  Doebeli M, and Hauert, C. (2005), Models of cooperation based on the prisoner’s dilemma And the snowdrift game. Ecol Lett 8: 748–766.
[6]  Essam El-Seidy and Heba K. Arafat (2013), On dynamics of randomly alternating prisoner's dilemma game (RAPDG). Applied Mathematical Sciences, Vol. 7, 2013, no. 67,3321 – 3333.
[7]  El Seidy, E. (2003), The adaptive dynamics for the randomly alternating prisoner’s dilemma game, Revista De La Uniόn Mathemática Argentinavol.44,1 99-108.
[8]  Hauert, C. Michor, F. Nowak, MA. Doebeli, M. (2006), Synergy and discounting of cooperation insocial dilemmas. Journal of Theoretical Biology 239: 195-202.
[9]  Hofbauer, J., and K. Sigmund. (2003). Evolutionary game dynamics. Bull. Am. Math. Soc40:479–519.
[10]  Leimar, O., Hammerstein, P., (2001), Evolution of cooperation through indirectreciprocation. Proc. R. Soc. London B 268, 745–753.
[11]  Maynard Smith J. (1964), Group selection and kin selection. Nature 201: 1145–1147.
[12]  Maynard Smith J. (1982) Evolution and the theory of games, Cambridge Univ. Press, Cambridge, U.K.
[13]  Nowak, M.A., Tarnita, C. E., Antal, T. (2010) Evolutionary dynamics in structured Populations Phil. Trans. R. Soc. B (2010) 365, 19–30
[14]  Nowak, M. A., and K. Sigmund.)2004(. Evolutionary dynamics of biological games. Science 303:793–799.
[15]  Nowak, M.A., 2006a. Evolutionary dynamics: exploring the equations of life. Belknap Press.
[16]  Nowak, M.A., (2006b(, Five rules for the evolution of cooperation. Science 314, 1560–1563.
[17]  Taylor, C. and Nowak, M.A. (2007), Transforming the dilemma. Oct 2007; 61(10): 2281–2292.
[18]  Traulsen, A., Nowak, M.A. (2006). Evolution of cooperation by multilevelselection. Proc. Natl. Acad. Sci. USA 103:10952–10955.
[19]  Tarnita, C. E., Ohtsuki, H., Antal, T., Fu, F. Nowak, M. A. (2009), Strategy selection in structured populations. J. Theor. Biol. 259, 570–581.