-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2014; 3(3): 35-40
doi:10.5923/j.jgt.20140303.01
Bi-Cooperative Network Games: A Solution Concept
Surajit Borkotokey , Loyimee Gogoi
Department of Mathematics, Dibrugarh University, Dibrugarh, India
Correspondence to: Loyimee Gogoi , Department of Mathematics, Dibrugarh University, Dibrugarh, India.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
We introduce the notion of a Bi-cooperative network game as a graph restricted Bi-cooperative game where interactions among players with bipolar motives are considered only through some exogenously given networks. Once such a network forms, the challenge rests on obtaining a suitable allocation of the payoff accrued by its members. In classical Network games the Position value is an important link based allocation rule. We extend this idea to define the Position value for the class of Bi-cooperative network games. It is then characterized using two axioms: efficiency (EFF) and balanced link contribution (BLC).
Keywords: Bi-cooperative game, Bi-cooperative network game, Position value, LG value
Cite this paper: Surajit Borkotokey , Loyimee Gogoi , Bi-Cooperative Network Games: A Solution Concept, Journal of Game Theory, Vol. 3 No. 3, 2014, pp. 35-40. doi: 10.5923/j.jgt.20140303.01.
Article Outline
1. Introduction
- In this paper we introduce the notion of a Bi-cooperative network game under a general setup that extends the earlier works of Gogoi et al. [3]. Such games engulf features of both Networks and Bi-cooperative games where the players support or oppose an issue through their links (we call them positive and negative links respectively). We also define the Position value as a link based allocation rule for this class. A characterization of the Position value is done with the axioms of efficiency (EFF) and balanced link contribution (BLC) in the line of Slikker [15]. A network describes the interactions among players through their links. Network games due to Jackson and Wolinsky [7] are network restricted Cooperative games. These games have their roots in graph restricted Cooperative games proposed by Myerson [11] where a Cooperative game is defined over only those coalitions where players are connected by some exogenously given network. Graph restricted games do not account for the network structure. In Network games [7], however the value function is defined over the sub-networks of a given network and thus the structure of the network is important. A Bi-cooperative game due to Bilbao [1] can be thought of as an extension of classical Cooperative game where players can support an issue, oppose it or remain indifferent. It assumes that the value accrued by a group of players (coalition) depends on the action of the remaining players with possibly few absentees. Thus the player set is divided into a partition of three groups: the positive contributors who support an issue, the negative contributors who oppose the issue and the absentees who remain indifferent to that issue. The characteristic function representing the game assigns a value to the positive contributors that depend on its opponents i.e., the negative contributors. Combining these two structures (networks and bi-cooperative) in [3], a Bi-cooperative network game is defined on a restricted domain where each group of positive and negative contributors is supposed to form components in the given network. These components resemble with the bi-coalitions of a Bi-cooperative game and therefore the model in [3] is seen to mimic the graph restricted games due to Myerson [11] under a bi-cooperative setup. However based on the different network structures owing to physical conditions, in the following we identify three types of situations that engulf the features of both Bi-cooperative and Network games. It can be easily seen that in [3] the situations pertaining to type (b) are only considered.(a) Players are positive or negative or indifferent as in ordinary Bi-cooperative games and consequently all the links of a positive player are termed as positive while the links of a negative player are negative and finally those of the absentees are considered indifferent. It is likely to have some links that connect a positive contributor to a negative contributor through which information may pass from one to the other.(b) Players and links both are either positive or negative so that we get a positive component or a negative component in the network.(c) Players may have links to the supporting network as well as to the opposing network simultaneously.Note that an essential assumption in the study of Bi-cooperative games is that a player can never be both a positive and negative contributor simultaneously, however in a Bi-cooperative network game that models situations of type (c) can have players who contribute to the network both positively and negatively through her distinct links. Consequently instead of calling her positive or negative we call her links as positive or negative links depending on their nature. This may be the case when players are connected to more than one networks with multiple identities. Examples can be found in [5, 9, 10].A solution in this paradigm will be a rational distribution of the worth (may be in terms of money, power and influence etc.) accrued by the given network. Network games under cooperative framework were introduced by Jackson and Wolinsky [7]. Two distinct solution concepts: the player based allocation rule and the link based allocation rule are found in the literature. However, unlike the classical Network game where it is the prerogative of the decision maker to choose between the player based and link based rules, in a Bi-cooperative network game such rules cannot be applied arbitrarily. For example, a link based allocation rule can be applied to all the three types while a player based rule applies only to type (a) and (b) but not type (c). It is worth noting that in [3] the Myerson value as a player based allocation rule is obtained along with some standard characterizations. Therefore in order to address the issues of all the three types mentioned above, in this paper we focus on a link based allocation rule: the Position value. Its counterpart in the network literature under cooperative framework is seen to be one of the most significant link-based allocation rules. Characterization of the Position value for Network games are found in [14-16].Various solution concepts of Bi-cooperative games have so far been proposed [2, 9]. Labreuche and Grabisch [9] have shown that the Bi-cooperative games proposed by Bilbao [1] inherits many identical characteristics from the multi-choice games defined by Hsiao and Raghavan [5] with three levels of participation. The major difference between the notions of Bi-cooperative and multi-choice games however lies in the fact that Bi-cooperative games are bipolar with the options of positive and negative contributions, while in multi-choice games, cooperations are along the same direction. Thus we find in [9] a new model of a Bi-cooperative game (as opposed to Bilbao et al. [2] that preserves such bipolarity and is not isomorphic to a multi-choice game. Labreuche and Grabisch [9] proposed the LG value as a solution concept that represents the share of the wealth obtained by some players after they decided on their participation to the game. Other values for Bi-cooperative games are also defined in [2] etc., however they mostly represent the net influence of a player in switching from one role to the other and is not specific to a particular coalition. In our present paper, we assume that the network is fixed and remain there for some time so that the players do not change their positions immediately. Therefore, the value given in [9] being specific to a particular partition of positive, negative and absent contributors seems to be more relevant here and thus we follow their approach. The rest of the paper is arranged as follows. Section 2 discusses the existing literature on Cooperative games, Network games and Bi-cooperative games in details. In section 3 we introduce the notion of a Bi-cooperative network game. Section 4 includes the main results of the paper and is followed by the concluding remarks in section 5.
2. Model Formulation
- In this section, we present the definitions and results necessary for development of our model. To a large extent this section is based on Labreuche and Grabisch [9], Jackson and Wolinsky [7] and Jackson [8].
2.1. Bi-cooperative Game
- Let
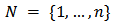 be a finite set of players. Let
be a finite set of players. Let 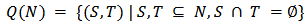 be the set of pairs of disjoint coalitions. We call every member
be the set of pairs of disjoint coalitions. We call every member 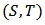 of
of 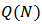 a bi-coalition. The underlying assumption is that players in
a bi-coalition. The underlying assumption is that players in 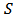 are positive contributors to the game, players in
are positive contributors to the game, players in 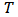 are negative contributors and those in
are negative contributors and those in 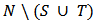 are absentees.Definition 1. A Bi-cooperative game is a function
are absentees.Definition 1. A Bi-cooperative game is a function 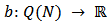 with
with 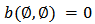 . The real number
. The real number 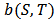 represents the worth of the bi-coalition
represents the worth of the bi-coalition 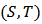 when players in
when players in 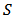 support an issue, players in
support an issue, players in 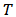 oppose it and the remaining players are indifferent.Let
oppose it and the remaining players are indifferent.Let 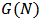 be the set of all Bi-cooperative games on
be the set of all Bi-cooperative games on 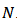 .Definition 2. A one point solution concept or a value for Bi-cooperative games is a function, which assigns to every Bi-cooperative game an
.Definition 2. A one point solution concept or a value for Bi-cooperative games is a function, which assigns to every Bi-cooperative game an 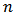 -dimensional real vector that represents a payoff distribution over the players.The LG value proposed by Labreuche and Grabisch [9] for Bi-cooperative games, denoted by
-dimensional real vector that represents a payoff distribution over the players.The LG value proposed by Labreuche and Grabisch [9] for Bi-cooperative games, denoted by 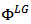 is defined as follows.For any
is defined as follows.For any 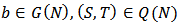 such that for all
such that for all 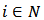

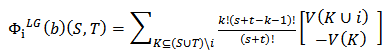 where for
where for 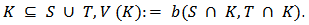 The LG value for a positive (respective negative) contributor depends only on her added-value from being indifferent to become a positive contributor (respectively negative contributor). The information regarding how this player behaves when she switches from positive to negative is not relevant, see [9].In [9], it is argued that a Bi-cooperative game is isomorphic to the multichoice game [5] with three levels of participation under the order relation
The LG value for a positive (respective negative) contributor depends only on her added-value from being indifferent to become a positive contributor (respectively negative contributor). The information regarding how this player behaves when she switches from positive to negative is not relevant, see [9].In [9], it is argued that a Bi-cooperative game is isomorphic to the multichoice game [5] with three levels of participation under the order relation  in
in 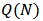 implied by monotonicity viz., for
implied by monotonicity viz., for 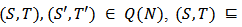
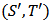 , iff
, iff 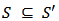 and
and 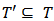 . Therefore alternatively they [8] have adopted the product order viz., for
. Therefore alternatively they [8] have adopted the product order viz., for 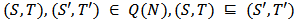 iff
iff 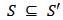 and
and 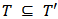 . Under this order
. Under this order 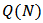 is an inf-semilattice with
is an inf-semilattice with 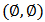 as the bottom element and all
as the bottom element and all 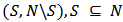 , the maximal elements. The product order relation distances the LG value from its multi-choice counterparts. Moreover it is specific to a particular bi-coalition. Therefore in this paper we follow the order considered in [9].Definition 3. For
, the maximal elements. The product order relation distances the LG value from its multi-choice counterparts. Moreover it is specific to a particular bi-coalition. Therefore in this paper we follow the order considered in [9].Definition 3. For 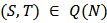 , the superior unanimity games
, the superior unanimity games 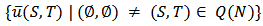 in
in 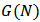 are given by,
are given by,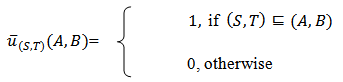 The above collection forms a basis of
The above collection forms a basis of 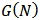 and so every
and so every 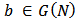 can be expressed as a linear combination of the superior unanimity games as follows,
can be expressed as a linear combination of the superior unanimity games as follows,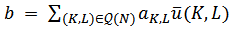 | (7) |
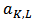 are the real constants.Following [13], we can associate to every
are the real constants.Following [13], we can associate to every 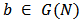 and each
and each 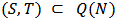 , a Cooperative game
, a Cooperative game 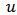 defined on
defined on 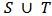 such that
such that 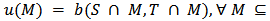
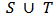 . So
. So 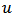 has a corresponding representation in terms of the unanimity Cooperative games
has a corresponding representation in terms of the unanimity Cooperative games 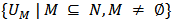 as follows, see [4, 13].
as follows, see [4, 13].
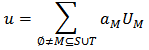 where
where 
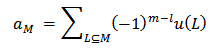 It follows that
It follows that
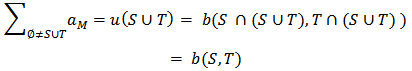 Now after some simple computations, we find the expression of the LG value for
Now after some simple computations, we find the expression of the LG value for 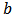 in terms of the Harsany’s dividends [4] for
in terms of the Harsany’s dividends [4] for 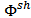 , the Shapley value [13] of the associated Cooperative game
, the Shapley value [13] of the associated Cooperative game 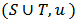 as follows,
as follows,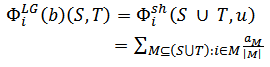 | (9) |
2.2. Network Game
- Let
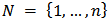 be a finite set of players. Let
be a finite set of players. Let 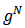 be the set of all subsets of
be the set of all subsets of 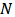 of size 2. We call
of size 2. We call 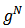 the complete network with
the complete network with 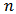 nodes. Let
nodes. Let 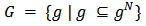 be the set of all possible networks on
be the set of all possible networks on 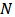 . By
. By 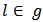 , we mean the link
, we mean the link 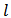 is in the network
is in the network 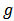 . For
. For 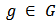 , we denote by
, we denote by 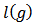 the total number of links in
the total number of links in 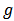 . Let
. Let 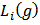 be the set of links that player
be the set of links that player 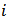 is involved in, so that
is involved in, so that 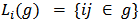 . We denote by
. We denote by 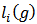 the number of links in player
the number of links in player 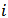 ’s link set. It follows that
’s link set. It follows that 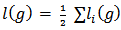 . Let
. Let 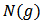 be the set of all players in
be the set of all players in 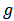 , i.e.,
, i.e., 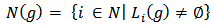 . For any
. For any 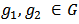 , denote by
, denote by 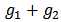 the network obtained through adding networks
the network obtained through adding networks 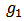 and
and 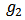 and by
and by 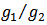 the network obtained from
the network obtained from 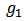 by subtracting its sub-network
by subtracting its sub-network 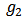 . A value function is a function
. A value function is a function 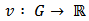 such that
such that 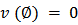 , where
, where 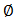 represents the empty network i.e., network without links. The set of all possible value functions is denoted by
represents the empty network i.e., network without links. The set of all possible value functions is denoted by 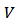 . The value function specifies the total worth that is generated by a given network structure. It may involve both costs and benefits whenever this information is available.Definition 4. A Network game is a pair
. The value function specifies the total worth that is generated by a given network structure. It may involve both costs and benefits whenever this information is available.Definition 4. A Network game is a pair 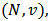 consisting of a set of players
consisting of a set of players 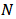 and a value function
and a value function 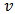 . If
. If 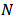 is fixed and no confusion arises about this, we denote the Network game by only
is fixed and no confusion arises about this, we denote the Network game by only 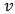 .Definition 5. An allocation rule is a function
.Definition 5. An allocation rule is a function 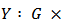
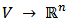 such that
such that 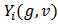 represents the payoff to player
represents the payoff to player 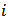 with respect to
with respect to 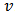 and
and 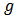 and
and 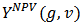 Definition 6. The unanimity value function
Definition 6. The unanimity value function 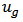 is defined by
is defined by 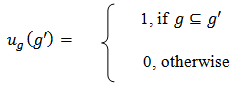 The unanimity value functions form a basis for
The unanimity value functions form a basis for 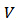 . Thus every
. Thus every 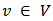 can be written as a unique linear combination of unanimity value functions
can be written as a unique linear combination of unanimity value functions 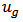 i.e.,
i.e., 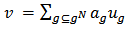 where
where 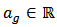 are called unanimity coefficients of
are called unanimity coefficients of 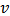 .Definition 7. Let
.Definition 7. Let 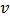 be a value function with unanimity coefficients
be a value function with unanimity coefficients 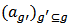 and network
and network 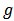 be given. Then the Position value
be given. Then the Position value 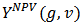 is defined by (see [15]).
is defined by (see [15]).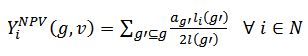 | (10) |
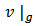 denote the associated Cooperative game with respect to the Network game
denote the associated Cooperative game with respect to the Network game 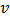 considering the links in
considering the links in 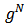 as players. It follows that for every link
as players. It follows that for every link 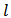 of
of 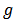 , if
, if 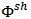 denotes the Shapley value [13] of the restriction
denotes the Shapley value [13] of the restriction 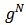 to the subsets of
to the subsets of 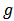 then we have,
then we have,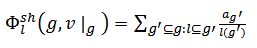 | (11) |
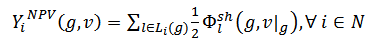 | (12) |
3. Bi-Cooperative Network Game
- In this section we introduce the notion of a Bi-cooperative network game. Let
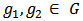 such that
such that 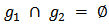 . The the pair
. The the pair 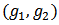 is called a bi-network. We assume that players in
is called a bi-network. We assume that players in 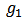 provide positive contributions and those in
provide positive contributions and those in 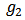 provide negative contributions. The rest are absentees. Let
provide negative contributions. The rest are absentees. Let 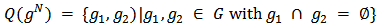 be the set of all bi-networks. For
be the set of all bi-networks. For 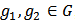 , we denote by
, we denote by 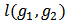 the total number of links in
the total number of links in 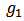 and
and 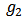 . Let
. Let 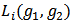 be the set of links that player
be the set of links that player 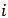 is involved in
is involved in 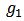 and
and 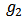 i.e.,
i.e., 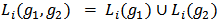 We denote by
We denote by 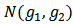 the set of all player in
the set of all player in 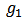 and
and 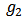 i.e.,
i.e., 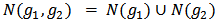 and
and 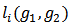 is the number of links of player
is the number of links of player 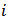 in
in 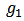 and
and 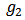 . A value function is a function
. A value function is a function 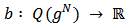 , with
, with 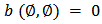 . Thus a value function assigns every member
. Thus a value function assigns every member 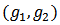 of
of 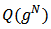 a real number its worth for which the nodes in
a real number its worth for which the nodes in 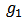 contribute positively to the network, nodes in
contribute positively to the network, nodes in 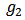 contribute negatively and the other remain indifferent. Note that here a node can have both positive and negative links simultaneously.Definition 8. A Bi-cooperative network game is a pair
contribute negatively and the other remain indifferent. Note that here a node can have both positive and negative links simultaneously.Definition 8. A Bi-cooperative network game is a pair 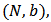 of a set
of a set 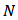 of players and a value function
of players and a value function 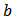 defined on
defined on 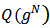 . When there is no ambiguity on the player set
. When there is no ambiguity on the player set 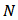 , we simply denote it by
, we simply denote it by 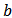 . The set of all Bi-cooperative network games is denoted by
. The set of all Bi-cooperative network games is denoted by 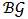 .Definition 9. An allocation rule for
.Definition 9. An allocation rule for 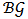 is a function
is a function 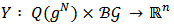 such that
such that
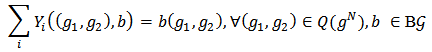 Where
Where 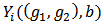 represents the payoff to the
represents the payoff to the 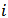 -th player with respect to
-th player with respect to 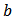 and the bi-network
and the bi-network 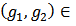
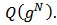 The following remark is important.Remark 1. An allocation rule of a Bi-cooperative network game assigns payoff to each of the players that is dependent on the value added to the game due to switching her roles from being indifferent to a positive contribution (or alternatively from negative contribution to being indifferent).
The following remark is important.Remark 1. An allocation rule of a Bi-cooperative network game assigns payoff to each of the players that is dependent on the value added to the game due to switching her roles from being indifferent to a positive contribution (or alternatively from negative contribution to being indifferent).4. Main Results
- Prior to the main result of the paper, we introduce the associated link game of a Bi-cooperative network game considering the set of links as a player set. Let
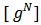 denote the set of hypothetical players representing the links in
denote the set of hypothetical players representing the links in 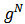 . Given
. Given 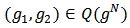 denote by
denote by 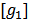 (similarly
(similarly 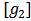 ) the set of all hypothetical players representing the links in
) the set of all hypothetical players representing the links in 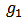 (similarly
(similarly 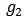 ). Given a Bi-cooperative network game
). Given a Bi-cooperative network game 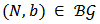 , define the associated link game
, define the associated link game 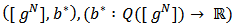 of
of 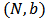 as follows. Given
as follows. Given 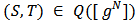 there is a
there is a 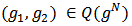 such that
such that 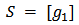 and
and 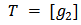 and
and 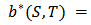
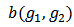 . Given
. Given 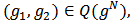 set
set 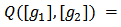
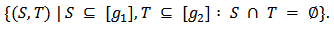 It follows that for
It follows that for 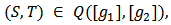 there is a
there is a 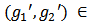
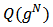 with
with 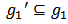 and
and 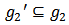 such that
such that 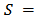
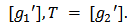 Definition 10. An allocation rule
Definition 10. An allocation rule 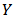 is called a link-based allocation rule on
is called a link-based allocation rule on 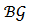 if there is some
if there is some 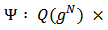
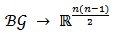 such that for all
such that for all 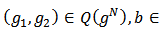
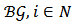

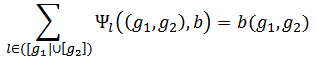 and
and
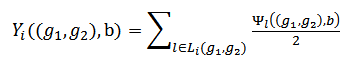 Definition 11. The Position value
Definition 11. The Position value 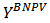 is the allocation rule according to which each player
is the allocation rule according to which each player 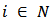 in a Bi-cooperative network game
in a Bi-cooperative network game 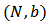 receives half of the LG value from each of her links considered as hypothetical players in the associated link game
receives half of the LG value from each of her links considered as hypothetical players in the associated link game 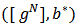 i.e.,
i.e.,
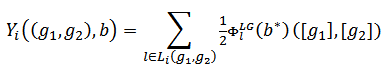
4.1. The Characterization of the Position Value
- Definition 12. An allocation rule
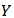 is efficient (EFF) if for any
is efficient (EFF) if for any 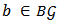 and
and 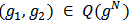 ,
, 
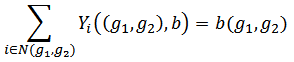 Lemma 1. The Position value satisfies EFF.Proof. The proof follows immediately from the denition of the Position value.For
Lemma 1. The Position value satisfies EFF.Proof. The proof follows immediately from the denition of the Position value.For 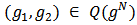 and
and 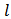 a link in
a link in 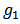 or
or 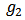 denote by
denote by 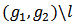 the bi-network
the bi-network 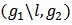 whenever
whenever 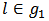 and the bi-network
and the bi-network 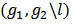 whenever
whenever 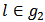 .Definition 13. An allocation rule
.Definition 13. An allocation rule 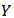 satisfies balanced link contribution (BLC) if for any
satisfies balanced link contribution (BLC) if for any 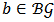 and
and 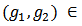 and
and 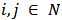 .
.
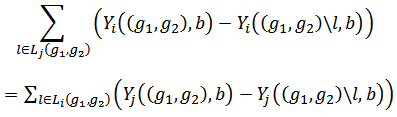 The property of BLC asserts that the net effect of loosing a link that contributes positively (or negatively) is same for its constituent players.1Lemma 2. The Position value satisfies BLC.Proof. Let
The property of BLC asserts that the net effect of loosing a link that contributes positively (or negatively) is same for its constituent players.1Lemma 2. The Position value satisfies BLC.Proof. Let 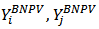 be the
be the 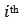 and
and 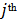 components of the Position value for a given
components of the Position value for a given 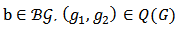 and
and 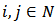 . It follows from (9) that,
. It follows from (9) that,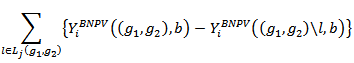
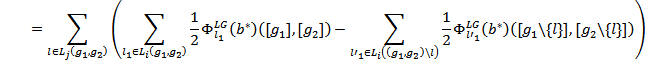
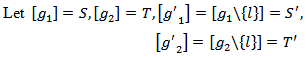
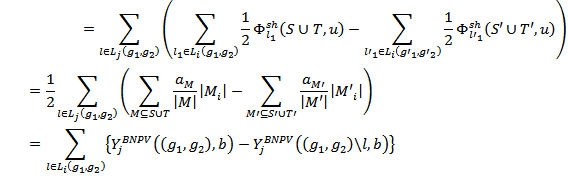 Where for each
Where for each  denotes the number of hypothetical players in
denotes the number of hypothetical players in  representing the links that involve player
representing the links that involve player 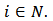 We have shown that the Position value satisfies two properties viz., EFF and BLC. Now we will establish that there is only one allocation rule satisfying these two properties.Theorem 2. The Position value YBNPV is uniquely determined by the axioms of EFF and BLC.Proof. The proof is by induction on
We have shown that the Position value satisfies two properties viz., EFF and BLC. Now we will establish that there is only one allocation rule satisfying these two properties.Theorem 2. The Position value YBNPV is uniquely determined by the axioms of EFF and BLC.Proof. The proof is by induction on 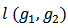 for
for 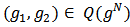 . Let
. Let 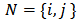 such that
such that 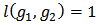 . Then either of the following holds.Case (a) :
. Then either of the following holds.Case (a) : 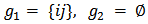 and Case (b) :
and Case (b) : 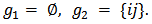 Case (a) : If possible let,
Case (a) : If possible let, 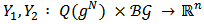 be two different allocation rules satisfying EFF and BLC. It follows trivially from BLC that,
be two different allocation rules satisfying EFF and BLC. It follows trivially from BLC that, 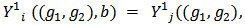 and
and 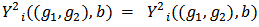 so that
so that 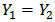 . Case (b) follows immediately from Case (a) and so the proof is omitted. Thus the result holds for a single link of positive or negative contributors.Let
. Case (b) follows immediately from Case (a) and so the proof is omitted. Thus the result holds for a single link of positive or negative contributors.Let 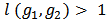 . For
. For 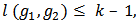 suppose that the allocation rule which satisfies EFF and BLC is unique for b. BLC, we obtaing the following.
suppose that the allocation rule which satisfies EFF and BLC is unique for b. BLC, we obtaing the following.

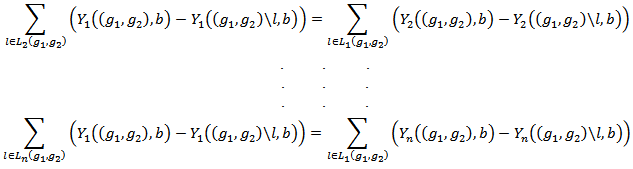 This would further imply that
This would further imply that
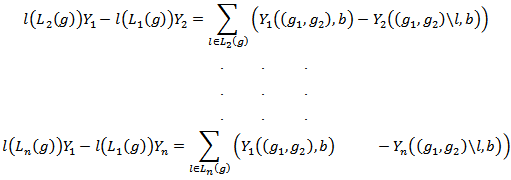 And by EFF, we have,
And by EFF, we have,
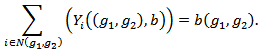 The above system of
The above system of 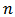 equations has
equations has 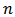 independent variables
independent variables 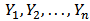 . It is customary to show that the system has a unique solution. Therefore, for
. It is customary to show that the system has a unique solution. Therefore, for 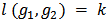 , the allocation rule which satisfies EFF and BLC is the unique allocation rule.
, the allocation rule which satisfies EFF and BLC is the unique allocation rule.5. Conclusions
- In this paper, we have introduced the notion of a Bi-cooperative game. The Position value as a link based solution concept is proposed. It is then characterized by the axioms of EFF and BLC. We have kept the nomenclature from their cooperative counterparts; however the concept and the formulation differ due to the presence of bi-polarity among the players within a network. In a future work we propose to study alternative characterizations in the line of [16].
ACKNOWLEDGEMENTS
- The work done in this paper is under the UGC Major Research Project UGC-India 42-26/2013(SR).
Note
- 1. Note that the BLC in classical Network games is different from that of a Bi-cooperative network game in the sense that the net effects of the links are considered over both positive and negative contributions of the game simultaneously on the basis of their presence in
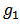 or
or 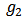 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML