1. Introduction

The interactions of more species that share the same territory influence the dynamics of individual populations and are assessed primarily with size and total number of individuals that compose them. Our attention will be focused on systems populated by two species only: predator and prey. The best known model that describes the predator-prey dynamics is the Lotka-Volterra model (A.N. Kolmogoroff 1936, N.S. Goel 1971, A.A. Keller 2011). This model is represented by a system of non-linear differential equations of first order (G. Sansone, and R. Conti 1964). An important aspect in the analysis of predator-prey model is the study of the behavior of the two populations on the long-time. This study involves the stability evaluation of the system solutions, that represent the conditions of equilibrium of the Lotka-Volterra model. Further advances in this field are given by F. Albrecht 1974, M. R. Cullen 1985, W. G. Wilson 1996, P. Augerm et al. 2002, X. Liu et al. 2003, A. E. Noble et al. 2011, K. Stankova 2013, K. Stankova A. Abate and M. W. Sabelis 2013, Ma Yi-An, and Hong Qian 2014, H. Zhang et al. 2014, A.S. Ackleh 2014.

Since the result of any interaction usually depends on behaviour adopted by the involved units, an appropriate mathematical tool to foresee the behaviour of such individuals is often described by means of game theory (J. Von Neumann in 1928). Therefore, a connection between Lotka-Volterra model and game theory for predator-prey game (N. Wolf and M. Mangel 2007, E. Altman 2014) in this paper is researched.

We have denoted predator and prey with symbols e (eater) and f (food) respectively. The initial conditions for each single interaction are: the two individuals are both located in a sufficiently small habitat, so that each of them is aware of the presence of the other and such that e is able to capture f. Labelling respectively by S_e and S_f the sets of strategies of predator and prey,

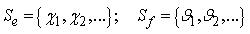(1.1)

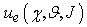we assume that: S_e ≡ S_f ≡ S, i.e. predator and prey have analogous strategies set (for examples: to be run, to be quiet, etc.) and can choose in S both analogous and different strategies. We denote with and 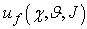the utility functions of predator and prey respectively and with J = {v₁, v₂, v₃, …} the set of parameters, which influence each single predator-prey game, for example: predator hunger, predator liking of the prey, physical efficiency of the predator versus the prey, the environmental conditions, the predator aggressiveness, the prey prudence, etc. (N. Serra 2014).

This paper is organized as follows: in Section 2 a generalization of utility functions of the single predator-prey game is introduced. In Section 3 a possible connection between utility functions and Lotka-Volterra model are proposed. In Section 4 the conclusions of this paper are presented.

2. An Extension the Predator-Prey Game

In this section we investigate on possible generalization of single interactions one on one, between predator and prey. The possibility to extend the single predator-prey game is to consider several interactions between predators and preys (or several games), which can happen simultaneously or not, between only two players at a time. Therefore, if we consider for every predator-prey game the utility functions values, in accordance with the strategies chosen by the players, we can define the utility functions for the predator and prey populations, which depend from all the utility functions of the singles predator-prey interactions. These utilities can be defined as the expected utility functions and indicated with 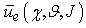and 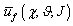such a that:

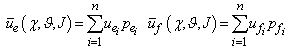(2.1)

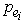in which n is the number of interactions between predators and preys, indeed and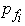are the probabilities of the predators to capture the preys and of the preys to escape the predators attack respectively in each game:

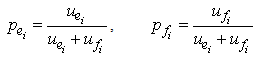(2.2)

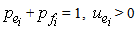with and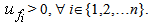

3. Expected Utility Functions and Lotka–Volterra Model

In this section, we have found a possible connection between expected utility functions and Lotka-Volterra model. If we denote by y the predator population and by x the prey population, in the absence of preys, y has an exponential decrease with negative rate -a₂₂, such that dy/dt = -a₂₂ y, while in the absence of predators, x has an exponential increase with a positive rate a₁₁, such that dx/dt = a₁₁x. Eventually, the coexistence of predators and preys results in an increase of growth rate of y, now given by a₂₁ x - a₂₂ and in a diminution of growth rate of x, now given by a_{11 -} a₁₂ y. These variations are proportional to the number xy of possible meetings between preys and predators, so we can introduce the following nonlinear differential equations system:

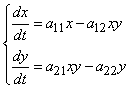(3.1)

The 3.1 are said Lotka-Volterra equations in which a₁₁, a₂₂, a₂₁ and a₁₂ are positive constants. The coefficients a₁₁ and a₂₂ can be interpreted as self interaction coefficients and depend by interactions of individuals belonging to the same population, or by absences of interactions (natural aging and death). They will not be considered in this study. Instead a₁₂ and a₂₁ can be interpreted as coefficients of predator-prey interaction, i.e. they can quantify the results of the interactions of predator-prey population. It is clear that a₂₁ is greater as greater is the ability of the predators to capture the preys, and a₁₂ is as smaller as greater is the ability of the preys to escape the predators.

We will consider only coefficients a₁₂ and a₂₁, since they are connected with the effective interactions between predators and preys. The utility functions can be viewed as measures of the effectiveness of an interaction, if correctly valued and the expected utilities (2.1), can be interpreted as the measure of the mean effectiveness of all the possible interactions. To start from 2.1, 2.2 we can consider three cases, for the expected utilities:

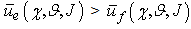(3.2a)

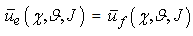(3.2b)

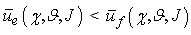(3.2c)

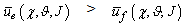• i.e. the predator population utility is greater than prey population utility. In this case there are more interactions between predators and preys in which the predators choose the best strategies in comparison to preys strategies or both predators and preys choose the best strategies but the predators have major probability to capture the preys in more interactions, because the parameters that influence the games are favourable to the predators. Therefore we can interpret the (3.2a) as an increase of the predator population and consequently a decrease of the prey population, in other terms, in this case we have an increase of a₂₁ and consequently an increase of a₁₂.

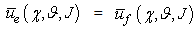•, i.e. the expected utilities of predator and prey populations are equal. In this case the predators number that choose the best strategies is approximately equal to preys number that choose the best strategies and the parameters that influence the games are favourable to predators and preys in the same way; or more predators choose the best strategies in comparison to preys, but in this case the games parameters are favourable to preys or vice versa, thus there are equals probability for the predators to capture the preys and the preys to escape the predators. Therefore we can interpret the (3.2b) as an equilibrium on favourable interactions number both to predators and preys, in other terms we have that a₂₁ and a₁₂ are constants

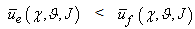•, i.e. the predator population utility is less than prey population utility, we deduce that in more interactions the preys strategies are best in comparison to predators strategies; or both predators and preys choose the best strategies but the preys have major probabilities to escape the predators and to survive, because the parameters that influence the games are favourable to the preys. In this case we can interpret the (3.2c) as an increase of the prey population and consequently a decrease of the predator population. In other terms we have a decrease of a₂₁ and consequently a decrease of a₁₂.

On bases of these considerations we can consider a₁₂ and a₂₁ directly proportional to:

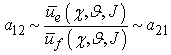(3.3)

By 3.3 we can rewrite 3.1:

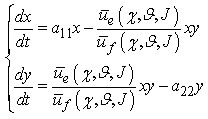(3.4)

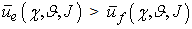For example by 3.4 if , the ratio of 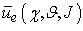and 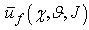is greater than 1, i.e. we have an increase of the predator population and consequently a decrease of the prey population, with an increase both a₁₂ and a₂₁ in equal measure. Finally the system 3.1 can have two solutions:

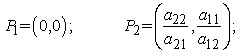(3.5)

These solutions define two equilibrium states in Lotka –Volterra model. By 3.3, we can rewrite 3.5:

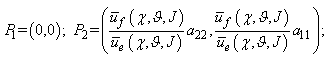(3.6)

The solution P₂ in 3.6 provides a possible connection between the equilibrium state in Lotka –Volterra model and the expected utility functions.

4. Conclusions

It has been observed that a possible generalization of the single predator-prey interaction was possible with the definitions of the expected utility functions of predator and prey population, considering several interactions between predators and preys (or several games), that can happen simultaneously or not, between only two players at a time. In this way we obtained of the indicators that describe if the number mean interactions is favourable to the predator or prey population. Since the payments obtained by player after a profile of strategic choices, both its own and its adversaries, can be interpreted in terms of adaptation, development, diffusion and of resources management, a possible connection between the expected utility functions and Lotka–Volterra model on predator-prey population dynamics, was found in this preliminary study. In fact we have observed that the coefficients a₁₂ and a₂₁ of Lotka-Volterra model can be considered proportionals to expected utility functions 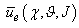and 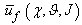respectively. Finally the object of future paper will be develop the present research and describe a possible connection between Nash equilibrium and equilibrium in Lotka-Volterra model.