1. Introduction

Sudoku puzzle, as a widely popular intellectual game in recent years, was invented in Swiss in 18th century. Then, it initially harvested well development in Japan in the pa st decades. The name Sudoku actually derives from Japanese that means “ Number Place”. Sudoku is a popular Japanese game with the objective of filling a 9x9 grid of cells with the numbers 1-9 without entering the same number in a column, row or and 3x3 sub-box of the grid. Some boxes have already been filled in by the setter to serve as clues. The rules are simple, but some puzzles can get very difficult, and it attracts fans from all over the world. Generally, Sudoku game is started with such a situation in grid that some of the cells have already been confirmed by digits known as givens. The task for Sudoku players is to place a digit from 1 to 9 into each cell of the grid, and meanwhile each digits can only be used exactly once in each row, each column and each block. Additionally, all the nine rows, nine columns and nine blocks are respectively ensured to contain all the digits from 1 through 9. These limitations for placing digits in three locations are respectively called row constraint, column constraint and block constraint; as in[2].

Based on the rules that we mentioned above, Sudoku players are commonly inspired to complete the placement of digits into all empty cells using various techniques as soon as possible. Previous research by Felgenhauer and Jarvis (Mathematics of Sudoku I, 2006) puts the total number of possible sudoku grids as66709037520210729 36960. This is approximately 6.671 x 10²¹. This number was calculated using various reduction methods and computer programs; as in[9]. This figure ha s been confirmed independently by numerous others[8]. Later Russell and Jarvis[5] showed that when symmetries were taken into account, there were, of course, many fewer solutions; 5,472,730,538 to be exact.

Another powerful conclusion shows that the minimal amount of givens in an initial Sudoku puzzle that can yield a unique solution is 17 given cells; as in[10]. Recently, researchers engaged in algorithm development issues some breakthroughs in Sudoku solving, grading and generating by Genetic Algorithm, evolutionary method with geometric crossover, belief propagation etc.; as in[11],[12],[13].

The researchers first counted the total number of possibilities for the first three rows, which turned out to be 948109639680. To make enumeration easier, th ey used many reduction methods such as relabeling, putting the first grid into standard form, and lexicographical reduction. Firstly, they reduced 948109639680 by 9! in order to put the first grid in standard form, yielding the answer 2672136. This can be further reduced by lexicographical reduction. This cuts down the number of top 3 rows that we are required to count by a factor of 72, to 36288. This was eventually reduced to 1296, 71 and finally 44; as in[1].

The final 44 classes can represent all the 2612736 different top 3 rows. The significance of the 44 classes is that every possible configuration of the top 3 blocks will have the same number of completions as one of the classes, and each member in every class has the same number of completions to a full grid. Thus, they can simply be placed into the same class for easier calculation. Each of the 44 classes is then enumerated, to find out the number of different completions to a full grid. Following that, the number is multiplied by the number of equivalent configurations to a full grid, totaled up and multiplied by 1881169920 ( 9!x72x72 ) for the total number of valid Sudoku grids; as in[8],[9],[10].

Sudoku most commonly appears in its 9x9 matrix form. The rules are simple: fill in the matrix so that every row, column, and 3x3 sub matrix contains the digits 1 through 9 exactly once. Each puzzle appears with a certain number of “givens.” The number and location of these determines the game’s level of difficulty. Figure 1 is an example of a 9x9 Sudoku puzzle. This puzzle idea can accommodate games of other sizes. Of course, a 4x4 puzzle would be easier and a 16x16 puzzle, harder. In general, any n x n game can be created, where n=m2 and m is any positive integer. In fact, the 25 x 25 puzzle is sometimes called Samurai Sudoku, because it is much more challenging and time -consuming. And there are numerous other variants of the game; as in[15].

2. Problem Analysis

Since Sudoku game is hugely attractive for worldwide players in different intellectual levels, it is significantly necessary for researchers to create puzzles tailored to the difficulty requests of players in a tolerable time. Meanwhile, these created puzzles must yield a unique solution so that players can complete the puzzles based on confirm ed cells using logic-deducing step by step. A puzzle with unique solution also shows sufficient intellectual challenges in the pursuit of terminal answer, and highlights the inherent charm of Sudoku game.

Thus, we develop a program to construct specific Su doku puzzles with the consideration of the following three requirements: as in[2].

2.1. Varying Difficulty

Essentially, the program should be able to create puzzles in different levels of difficulty. It regulates that the program for creating must be designed by means of two jobs as follows:

• Difficulty level: define what the difficulty level is, and evaluate a fixed Sudoku puzzle by a grading program.

• Extensibility: A varying number as a metric of difficulty request from a play can be input by the player. Based on this number, the algorithm for creating must be applicable to generate diverse puzzles satisfying the difficulty request of the player.

2.2. Unique Solution

All generated Sudoku puzzles must be guaranteed to yield a unique solution by a solving algorithm.

2.3. Minimizing Complexity

The programs of all these algorithms must finish their jobs in a short time accepted by users or players.

2.4. Assumptions

• We scale the game environment of a Sudoku puzzle within a 9 -by-9 grid, and take no consideration of the Sudoku puzzle in other size of the grid.

• All the statistic data of the running time in this paper are counted by our computer. These data have reliable statistic values and comparability since they are collected under the same computational condition.

2.5. Computational complexity of the Sudoku Problem

The computational complexity for a Sudoku problem is analytically valuable, in fact, at every step there is always a cell that can be filled only with a number, than the complexity results O(n^2),where n is the number of cells for each row or column,(in our case n=9).

Instead, for a generalized Sudoku problem (a Sudoku problem that has not a uniqu e solution) the computational complexity is not easily valuable analytically but may be evaluated by comparison with the corresponding one of a problem, the mathematical complexity of which has been evaluated and is known; as in[3],[4] .

3. Mathematical Model to Describe Sudoku

3.1. Variables in the Mathematical Models

To describe a mathematical model first of all variables and their kind (for example binary, integer.) should be defined.

In this model a 3D matrix 9x9x9 of variables is defined, with a total amount of 729 elements. Each so defined variable is binary and characterized by three indexes: i , j , k: the index i and j define respectively the row and the column of a generic position in a Sudoku schema; the index k represents integer in the range 1 to 9 which may be present in a generic position. Being the variables binary they can assume only the values 0 or 1: 0 value is assumed if in the position i, j, the k integer is not included and the value 1 if the position i,j is filled with the k integer.

3.2. The Objective Function

In this point an “objective function” to be minimized or maximized should be define d. But one must remark that in our case one need to determine only an admissible solution, because every Sudoku schema has one and only one solution: then the admissible solution is automatically the optimal one.

As a consequence the value of objective function is out from our interest and a generic constant value may be assumed like “objective function”, for instance the unit value.

3.3. Constraints

The constraints, necessary to limit the field of the problem, are linear combinations of variables giving a constant value.

The model contains the following typology of constraints:

1. Having fixed a j column, at the crossing of each row i with the j column, the sum of variables included within correspondent k column shall assume unit value;

2. Within the matrix i,k the sum of variables along i for each k assumes unit values.

3. Having fixed an i row, at the crossing of each column j with the i row, the sum of variables included with i correspondent k column shall assume unit value.

4. Within the matrix j,k the sum of variables along i for each k assumes unit value.

5. For every sub-matrix 3x3 (i,j) the sum of variables for each k shall assume unit value.

Of course all the previous constraints define an empty Sudoku schema ; but if we want to introduce in the schema some predefined values in predefined position, the corresponding values shall be also predefined assuming the unit value; nothing to say that such predefined values shall respect the above defined restraints; as in[3],[4],[6],[7].

4. Mathematical Formulation of the Model for Sudoku Game

The mathematical model of Sudoku game above defined in terms of variables, objective function and restraints is described by the following expressions

Variables: X_i,j,k binary i=1...9, j=1...9, k=1...9

Objective Function: min 1

Constraints:

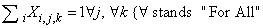
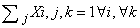
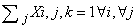
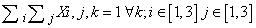
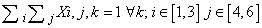
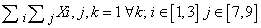
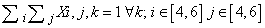
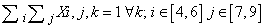
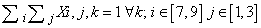
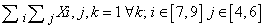
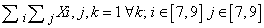
5. Implementation of the Model with Instance Generation Program

To apply practically the Sudoku program, an instance generation program has been written in C++ language; this program is able to generate a Sudoku game having chosen the number of fixed parameters to be introduced, the position of which is def ined by the program by means of a random generator; a second program assigns the predefined integers to the position chosen as above described. In the following pages the instruction of the programs are reproduced.

This program gives in output a generalized Sudoku instance, but we cannot be sure that this instance has a unique solution.

5.1. Comparison with Existing One

To generate an instance with unique solution the following method, developed by Professor Della Croce and professor Ferro of Politecnico di Torino is used.

Suppose that the model presented above has been solved and a feasible solution has been found. Denote by SOL(i,j) the value of the element (i,j) of the schema in the feasible solution. Solve the following model P2:

Variables: Xi,j,k binary i=1...9, j=1...9, k=1...9

Objective Function: min

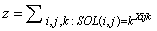Constraints: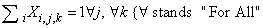

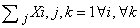
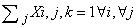
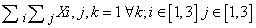
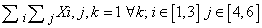
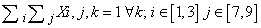
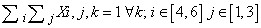
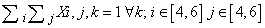
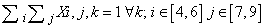
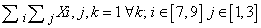
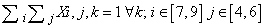
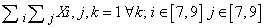The solution of this model provides a feasible solution also to the previous model. The objective function of model P2 minimizes the sum of the elements in the grid having the same value obtained in the solution of the previous model. Hence, as each grid is composed by 81 elements, if the objective function value of model P2 is equal to 81 (Z=81), then the Sudoku problem has unique solution, else it has not.

5.2. Solving Algorithm: Depth-first Search

An effective solving algorithm for searching out all the feasible solutions of a Sudoku puzzle is indispensible for the generating algorithm to judge whether a created puzzle ha s a unique solution. Since a Sudoku puzzle is shown as a 9 -by-9 grid with sufficient information from givens and strict constraints of game rules, it is feasible to search out all the solutions of the puzzle using enumerating search.

For finding out a solution as a terminal pattern or judging whether a created puzzle is unique-solvable, we build a Sudoku solver by the mechanism of Depth -first search. The solver searches empty cells from left to right, top to bottom in the grid. It attempts to fill a potential 1-through-9 digit in each empty cell while satisfies the three constraints of game rules. Once none of digits from 1 through 9 can be filled in an empty cell to meet the constraints, the solver backtracks to the previous empt y cell and substitutes the filled digit there into another untried potential digit. In this way the solver continuously performs the search until all the potential solutions are searched out and recorded.

6. Results

Based on the specification of algorithms above, we create Sudoku puzzles in different levels respectively within tolerable time using our developed solving and generating algorithms while guarantees each of these puzzles has a unique feasible solution.

Our algorithm finds at least one feasible solution, if it exists. Originally, we assumed each Sudoku puzzle has one unique solution since usually an answer is provided with each puzzle. However, after playing a few games, we discovered that uniqueness is not a requirement for puzzle creators. Some puzzles have multiple solutions. In such cases, our solution was correct but distinct from the solution provided by the puzzle creators.

7. Analysis of Algorithm Complexity

For generating Sudoku puzzles we develop an algorithm with negligible space co mplexity. Thus we concern significantly about time complexity of our algorithm, and focus on reducing it in order to achieve the generation of Sudoku puzzle within tolerable time for players.

The entire algorithm for generating Sudoku puzzle is divided into two parts: to create a terminal pattern and then to dig holes on it. The time complexity of creating a terminal pattern proves to be O(1) , which indicates that a terminal pattern can be produced within constant- magnitude time. In the algorithm of generating puzzles, the program does trials of digging a hole at most 81 times in the terminal pattern. For the uniqueness feasible solution derived from the constructed puzzle, a solver built by the Depth-First Search is called to find out all potential solutions of the dug-out puzzle once a trial of digging a hole is done at an unexplored cell. The time complexity of the Depth -First Search proves to be Θ(V + E) as in[14]. The amount of (V + E) in the problem of solving a Sudoku puzzle is estimated to be less than 1500000.

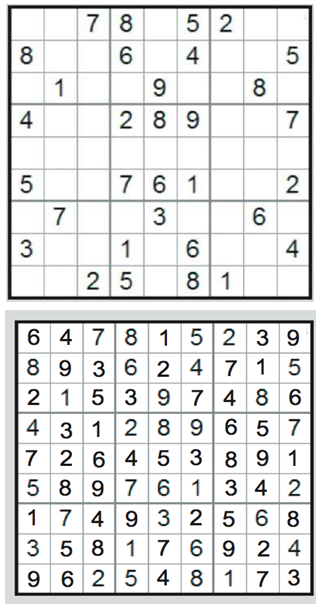
8. Examples

In this paper some examples of Sudoku instance on which our model has been tested will be given.

Example of Sudoku and its solution.

Another example with their solution is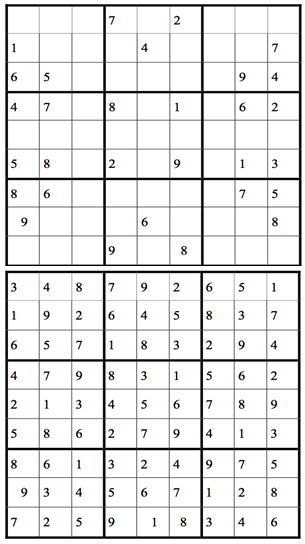

9. Conclusions and Future Developments

The Sudoku mathematical game, born about two centuries ago, but largely spread in World only during the last years, has been studied and analysed in details.

Our model is very efficient, because it is able to solve every Sudoku instance in a very short time; it takes 0.2 seconds to 0.5 seconds for the diabolic ones according to their difficulty levels. This fact shows that the different difficulty between two levels affects the performance of a human solver but not that of the program.

A mathematical model has been formulated. In addition, the mathematical model has been implemented in a computer solver and in parallel a program has been developed able to generate Sudoku games. Some applications of this analytical and numerical work have been presented too.

Further developments in this field should consider the uniqueness of solution in r elation to the minimum number of input data necessary for this condition.

ACKNOWLEDGEMENTS

The authors are thankful to the reviewers for their suggestions to improve the present paper.