1. Introduction

In the literature, there are many solution concepts to the problem of payoff allocation arising from a transferable utility cooperative game (or simply a game) when players are grouped according to a fixed coalition structure; especially core solutions (see[1]) and bargaining set solutions (see[2],[3] or[4]). Given a coalition structure, the core plays a central role and generally is a subset of many other solution concepts. For instance, given a game and any coalition structure, it is well-known that the (standard) bargaining set 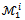as defined in[2] is a superset of the core. Due to its characterization by a unique set of predefined linear inequalities, the core is surely the most tractable solution concept. It is then important to look for ideal situations where the core is equivalent to a given solution concept.

It is shown in[5] that when the core of a game with less than five players is nonempty (the game is balanced), it coincides with the bargaining set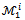. This proves that the bargaining set of a balanced game with less than five players is a polyhedron instead of a union of several possibly non disjoint or empty polyhedra (see[6] for a full description of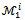). Roughly, the multitude of polyhedra that make up the bargaining set of a balanced game with less than five players collapses in a unique polyhedron, the core.

In this paper we prove that the same result holds when we replace the core by the objection-free core which is the set of all imputations with no bargaining set type objection.

Moreover, the objection-free core for any coalition structure is a superset of the core, is a unique polyhedron when it is nonempty, is a subset of the bargaining set 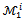and for less than five player games, the objection-free core coincides with 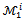whenever it is nonempty.

The remainder of the paper is organized as follows : in the next section devoted to the model, core and bargaining set concepts are presented and the notion of objection-free core is introduced. In section 3, the relationship between the core and the objection-free core is studied as well as the relationship between the objection-free core and the bargaining set. Section 4 concludes the paper.

2. The Model

2.1. The Core and the Bargaining Set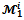

Consider a nonempty finite set N of n players. Denote by 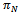the set of all partitions of N and by 2^N the set of all nonempty subsets of N. Hereafter, a partition N is called a coalition structure and elements of a given coalition structure are called blocs. In order to simplify notations, coalitions will sometimes be written without braces; for example the coalition {i,j} will be denoted by ij, N\{i,j} by N\ij, ...

A transferable utility cooperative game is a pair (N,v) where N is the set of players and v is a map, called the coalitional function, from the power set of N into the set 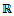of real numbers such that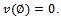For any nonempty subset S of individuals, v(S) is the gain (or the cost if it is negative) obtained by members of S when they are grouped in S.

For a coalition structuretwo players i and j are partners if i and j belong to the same bloc of and a payoff allocation is any vector 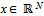such that 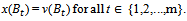Given a payoff allocation x and a coalition S, let x(S) = 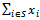with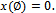 Note that x(S) is the total payoff allocation of the coalition S over the payoff allocation x. The excess of a coalition S over x, is the real number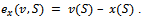The excess 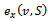measures the dissatisfaction of the coalition S over the payoff allocation x.

For a game (N,v) and a coalition structure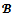, a 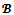-imputation is a payoff allocation 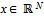such that 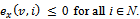The set of all imputations for the coalition structure 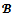is denoted by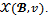Note that :

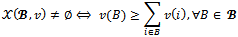Given a coalition structur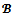e, the 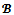-core, denoted by 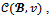is the set of all 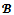-imputations x such that, 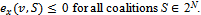A profile of balancing weights is any collection 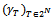of real numbers such that

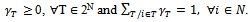A game (N,v) is 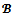-balanced if for any profile of balancing weights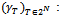

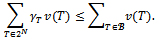When individuals form the grand coalition - that is 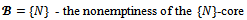(or simply the core) is stated in the following Bondareva-Shapley theorem ([7] and[8]).

Theorem 1 A necessary and sufficient condition that the core of a game (N,v) is not empty is that the game is {N}-balanced.

The Bondareva-Shapley theorem is still valid for any coalition structure 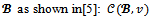is nonempty if and only if the game is 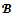-balanced. This clearly shows that core imputations may not exist for some games. Bargaining sets are alternative solutions to overcome the possible emptiness of the core.

Roughly speaking, bargaining sets select imputations that are stable via a certain bargaining possibilities of the players. In the case of the Aumann-Maschler bargaining set, given a coalition structure 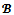and a couple (i,j) of partners, an objection of i against j over a 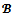-imputation x is any couple (S,y) such that

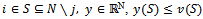and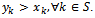

Remark 1 As stated in lemma 2.1 in[6], given two players i and j, an imputation x and a coalition S, there exists an objection of i against j over x using the coalition S if and only if i and j are partners,

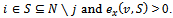A counter-objection of j against the objection (S,y) of i against j over x is any couple (T,z) such that 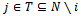and 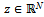satisfies

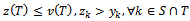and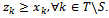

The Aumann-Maschler bargaining set is the set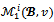of all stable 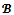-imputations in the sense that a 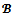-imputation x is stable if any objection over x has at least a counter-objection. The bargaining set is nonempty for almost all coalition structures as stated in the following theorem (see[9]):

Theorem 2 Given any game (N,v) and any coalition structure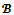, the bargaining set 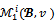is nonempty whenever the set of 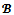-imputations is nonempty.

Theorem 2 provides the main structural difference between the core and the bargaining set: while only the core of a balanced game is nonempty, the bargaining set given any coalition structure is always nonempty whenever the set of imputations is nonempty.

2.2. Objection-Free Core

Although the nonemptiness of the bargaining set is proved, the remaining difficulty is a simple determination or description of all imputations that belong to the bargaining set. According to the definition, a basic way to obtain a subset of the bargaining set consists in considering only imputations with no objection.

Hereafter, given a game (N,v) and a coalition structure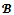, the set of all 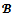-imputations with no objection denoted by 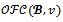is called the objection-free 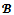-core. Clearly the objection-free 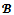-core is contained in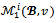for every coalition structure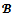. Moreover at core imputations there is no objection. As a consequence the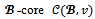is contained in the objection-free 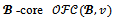for every coalition structure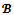. It is then straightforward that:

.

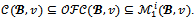By definition of an objection, a coalition S involved in an objection separates at least a couple of partners. That is there exists two partners i and j such that 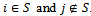We then split 2^N into two subsets: (i) 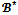collects all blocs and all coalitions that separate at least a couple of partners; and (ii) 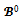consists of all coalitions other than blocs that do not separate partners. More formally, a coalition 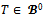if and only if T is not a bloc and for any couple (i,j) of partners with respect to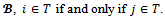It then follows that 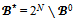with :

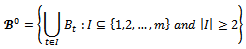With the notation above, it is straightforward from remark 1 that:

Proposition 1 For any game (N,v) and for any coalition structure,

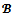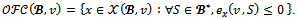Clearly, the objection-free core is defined by a unique set of linear inequations (and equations); therefore is a polyhedron when it is nonempty.

3. Results

3.1. The Core and the Objection-Free Core

As mentioned above, the core is a subset of the objection-free core. The following example shows that the core and the objection-free core may be distinct sets of imputations.

Example 1 Consider the following four-person game (N,v) defined by v(i) = 0 for all 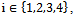v(S) = 2 if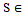 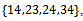v(S) = 3 if 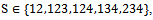, v(13) = 6 and v(1234) = 7. Let 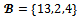be the coalition structure. One can easily check that 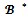= 2^N \ {24,123,134,1234} and that 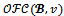= {( 3,0,3,0)}.

Moreover any 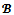-imputation satisfies x₁ + x₃ = 6 and x₂ = x₄ = 0. Thus x(1234) = 6 < v(1234) = 7 and then 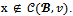Clearly the objection-free core with respect to 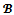is nonempty while the core is empty.

Proposition 2 For any game (N,v) and for any coalition structure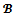, if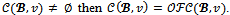

Proof. Suppose that 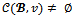and consider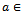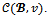To prove that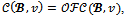it is sufficient to prove that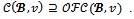Consider any imputatio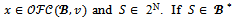n then 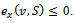Now if 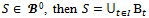for some 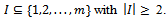Then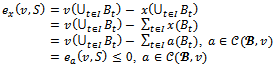

In both cases, 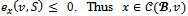and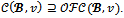

Proposition 3 Consider a game (N,v) and a coalition structure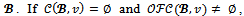then 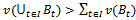for some 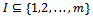with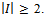

Proof. Suppose that 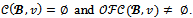Then there exists 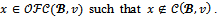Sincesuch that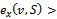 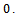By proposition 1, it follows that 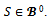Therefore 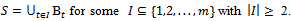Note that x is a 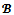-imputation. Thus

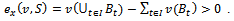Proposition 3 shows that the core and the objection-free core are distinct only for non efficient coalition structures for which some blocs may gain more when their members form a unique bloc.

Given a game (N,v) and a coalition structure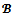, define a new game 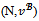as follows:

Remark 2 For any game (N,v) and for any coalition structure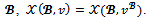In fact by definition, 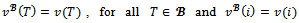for all 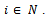The equality between the two sets then immediately follows from the definition of a 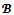-imputation in both games.

Proposition 4 For any game (N,v) and for any coalition structure

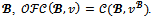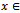
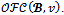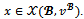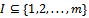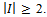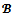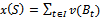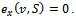Proof. Consider and suppose thatThen by remark 2, First assume thatfor some with Any two distinct blocs are disjoint and x is a -imputation. Thus andNow assume that 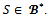By definition of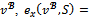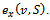Since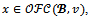 it follows from proposition 1 that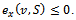. In both cases, 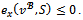Hence 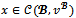and

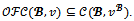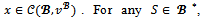
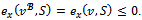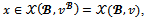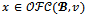Now assume that.Sincethen and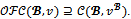

Note that payoffs for coalitions in 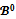are inessential for the objection-free core 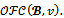This mainly justifies the result in proposition 4 since the game 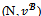does not depend on

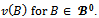To generalize the notion of balancedness, consider any nonempty subset E of 2^N and define a profile of balancing weights over E as any collection 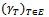of real numbers such that 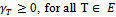and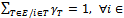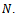In particular, any profile of balancing weights over 2^N is simply a (standard) profile of balanced weights presented in section 2. Moreover, a game (N,v) is almost 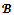-balanced if 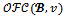is nonempty.

Proposition 5 For any game (N,v) and for any coalition structure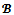, the game is almost 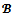-balanced if and only if for any profile of balancing weights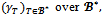

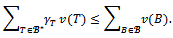Proof. Suppose that the game (N,v) is almost 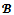-balanced. Let 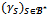be a profile of balanced weights over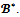Pose 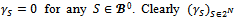is a profile of balanced weights. Since the game is almost 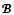-balanced, by proposition 4 the game 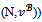is 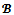-balanced. Therefore, 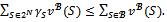Since 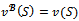for all 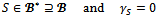for any 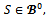then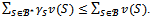

Conversely suppose that for any profile 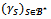of balanced weights over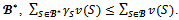If 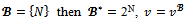and the game (N,v) is balanced. Now suppose that the coalition structure contains at least two blocs. Let 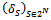be a profile of balanced weights. Observe that

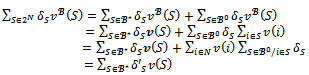where for each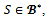

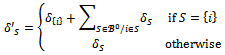
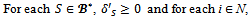
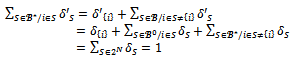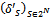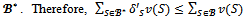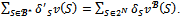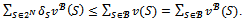This proves that is a profile of balanced weights over. by assumption. ButThusThus the game 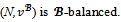By proposition 4, the game is almost 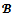-balanced.

3.2. The Bargaining Set and the Objection-Free Core

The game 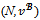has the same core with the game (N,v). The two games also share the same bargaining set as shown below.

Proposition 6 For any game (N,v) and for any coalition structure

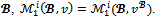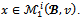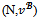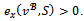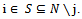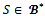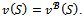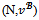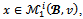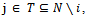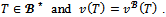Proof. Suppose that.Consider any pair {i,j} of partners and any objection (S,y) in the game of i against j at x. By remark 1, Note that i and j are partners andTherefore and then. The objection (S,y) of i in the game is also an objection in the game (N,v) of i against j at x. Since there exists a counterobjection (T,z) in the game (N,v) of j against (S,y). Since then Therefore (T,z) is also a counterobjection of j against the objection (S,y) of i in the game

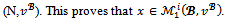In the same way, we prove that any imputatio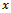n in 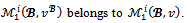This is clearly due to the fact that both games have the same set of objections and counterobjections on

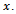It is known from[5] that for games with less than five players, when the core for any coalition structure is nonempty, it coincides with the bargaining set.

Theorem 3 For any game (N,v) with less than five players and for any coalition structure 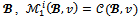whenever

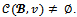The next theorem states that this result can be extended to the objection-free core.

Theorem 4 For any game (N,v) with less than five players and for any coalition structure 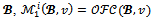whenever

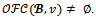Proof. Suppose that 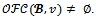for a game with at most four players. Then by proposition 4,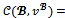 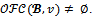Since the game has at most four players, 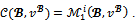By proposition 6,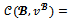 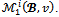That is

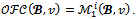As mentioned above, the objection-free core is a subset of the bargaining set. It may be a proper subset of the bargaining set as it is the case with the following example brought to our attention by Solymosi.

Example 2 Let N = {1,2,3,4,5} and consider the game (N,v) defined as follows: v(S) = 5 if 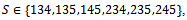v(S) = 6 if | S | = 4, v(S) = 10 if S = N and v(S) = 0 otherwise. For the grand coalition, that is when 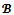= {N}, one can check that x = (2,2,2,2,2) belongs to the core (which then coincides with the objection-free core) and that (5,5,0,0,0) belongs to the bargaining set; but is not a core imputation.

3.3. The Core and the Bargaining Set

Let (N,v) be a game and be a coalition structure. Given a collection 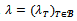of real numbers, define the game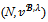as follows: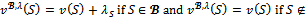

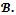Note that the game 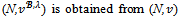by increasing (or decreasing) only the share of some blocs.

We prove that when each 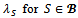is sufficiently large, the core and the bargaining set for the game 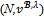coincide. This shows that the coincidence of the core and the bargaining set of a game depends on the adequacy of goods available in blocs to yield any bargaining set imputation without any positive excess.

Proposition 7 Consider a game (N,v), a coalition structure 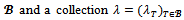of real numbers. Assume that

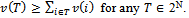If for each 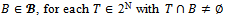and for any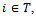

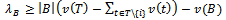(1)

then

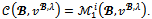Proof. Assume that 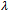satisfies (1). For 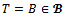in (1), 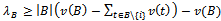for each 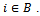Writing this inequality for each 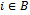and summing together right-hand terms, we deduce that

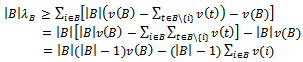By dividing both terms of the latter inequality by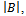we deduce that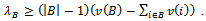Since 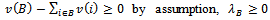for each

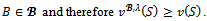Consider any imputation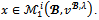Suppose that 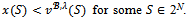Note that 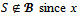is a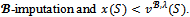Consider any player 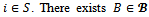such that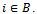Denote by j a player in 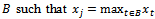.Then for all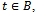 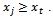Thus 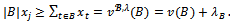Hence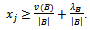

Suppose that

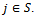Then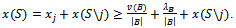Since x is an imputation, for each 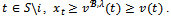Then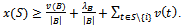By assumption on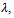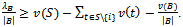Therefore 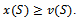A contradiction arises.

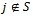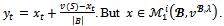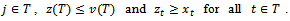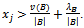Therefore and (S,y) is an objection of i against j over x whereThen there exists a counter-objection (T,z) against the objection (S,y) of i against j over x. By definition of a counter-objection, Then by definition of j, As shown for 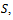one can easily check that 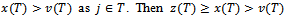and a contradiction arises. Therefore there exists no counter-objection to (S,y).

We have shown that if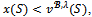, then there exists a justified objection of a player against a patner over x. This is clearly a contradiction since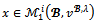. In conclusion, 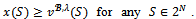Therefore 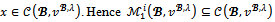and then

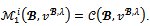Proposition 8 Consider a game (N,v) with at most four players and a coalition structure

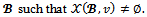If 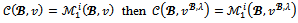for all collection 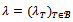of real numbers such that

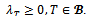Proof. Suppose that (N,v) is a game with at most four players and let 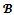be a coalition structure such that 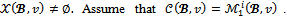Now consider any collection 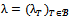of real numbers such that

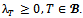Since 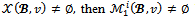by theorem 2. But 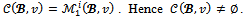Consider any imputation 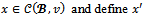as follows:

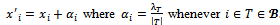Note that 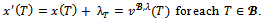Thus 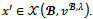Moreover, for any coalition S that is not a bloc, 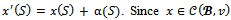and 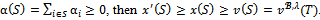This proves that

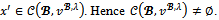Recall that there are at most four players. Since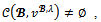we conclude by theorem 3 that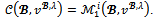

4. Conclusions

Theorem 4 is an improvement of an earlier result due to[5]. It enlarges the family of games with a tractable bargaining set. The core is nonempty only for some efficient coalition structures for which the game is balanced. Our result is still valid for some non efficient coalition structures and it is equivalent to Solymosi's result for efficient coalition. Moreover, we show that the core and the bargaining set coincide as soon as we sufficiently enlarge the gain of blocs.

ACKNOWLEDGEMENTS

We wish to thank Tamás Solymosi for providing us very illustrative examples.