Alessandro Morselli
Lecturer of Institutions of Economics and Economic Policy, Department of Human and Social Sciences, University of Messina, Italy
Correspondence to: Alessandro Morselli, Lecturer of Institutions of Economics and Economic Policy, Department of Human and Social Sciences, University of Messina, Italy.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The following work evidences an economic and political interdependency of the countries in the EMU which push the national governments to adopt, on an international level, strategic actions that are material in defining their policies in function with the policies and initiatives of the others. The relative efficiency of the budget strategies is shown by the two-countries model. The policies of the national budget, adopted in the context of the EMU, risk having a limited efficiency to the difficulty encountered in forming cooperation agreements and to financial rigour imposed by the European Stability Pact. These notable factors may stimulate interest in solutions of a transnational description.
Keywords:
European Monetary Union, European Central Bank,Structural Interdependency, Fiscal Policy, Nash Equilibrium
Cite this paper: Alessandro Morselli, Cooperative or Non-cooperative Solution to an Optimal Fiscal Policy in the European Monetary Union, Journal of Game Theory, Vol. 2 No. 2, 2013, pp. 9-12. doi: 10.5923/j.jgt.20130202.01.
1. Foreword
The national budget policies adopted in the context of the European Monetary Union (EMU), risk having limited effect, especially due to difficulties encountered in the creation of the cooperation agreements and due to the financial rigour imposed by the Stability Pact. These factors may enhance the interest in solutions of a transnational description. Strategic analysis is set in the context of a model based on two countries, as forwarded by J.H Bryson[1]. This considers those responsible for the policies (the governance) of the budget as two players able to make perfect previsions. Their actions may not be cooperative with the measures in which the budget’s policies are decided at the level of individual countries[2]. However the sub-optimal results of the equilibriums resulting from these strategies can push us to examine cooperative solutions.The model therefore defines the objectives of the budgets’ governance in the member countries of the EMU and describes the relationships which set objectives and instruments of taxation.It is hypothesised that the EMU is formed by two countries (Italy and France) which adopt the Euro and both of which maintain relations with the rest of the world. The budget’sgovernance in each of the two countries set themselves the internal objective shown from the value of a global product, respectively Yº and Y* and a goal of balancing the commercial balance Bºc o B*c = 0.Pursuit of the external objective can be justified with the necessity for each country to contribute to the stabilisation of a Euro exchange rate or by the desire to control active foreign stock, the variation of which depends on commercial balance. These objectives are independent of the stability of prices which the European Central Bank (ECB) proposes.From the moment that the budget’s governance set up only one instrument of intervention, they cannot pursue their two objectives contemporaneously. The consequence would be to damage the national community and the governance want to minimize this.It is assumed that the respective damages for the authorities, of Italy and of France, are defined in Bºc o Bc = 0; for which Π and Π*: 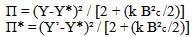 | (1) |
In expression (1) the square of the margins of global products (Y) and (Y’) and of the commercial balances Bc and Bc*, in relation to their desired totals, are measured by the same coefficient (1) and (k). Their relative resultant values relate the importance accorded by the authorities to one or the other objective.
2. Existing Relationships between Objectives and Instruments
The relationship between the objectives and the instruments of the budget’s policies are derived from the reduced form of the model which describes structural interdependency of European countries, that form a type of small monetary union and which are linked to the rest of the world by flexible exchange.This analysis includes the relations of determination of global products on the basis of the respective demands, the equality between the supply and demand of Euro and the specification of the commercial and financial relations between the EMU and the rest of the world. It is hypothesised that the European interest rate defers from the international interest rate, this interprets a greater integration between the European financial markets. In this context, an increase in public spending (G) or (G*), in one of the European countries and its financing through debt would produce:1) An increase in the relative national production and a commercial deficit compared to the rest of the world. In effect, the demand for national goods is boosted by national public expenditure and, on the other hand, reduced by the increase in the European interest rate. The rise in this rate and an increase in the national product respectively bring an influx of capital and a commercial deficit which determines, depending on their relative rises, an appreciation or depreciation of the Euro. It is supposed that an eventual increase in the Euro exchange rate in relation to other currencies acts as a brake on the commercial deficit. 2) A reduction of the productive process in the other country and an improvement of its commercial balance. In effect, the rise in the European interest rate instigates a decline in the demand for production. This effect is enforced, or reduced, by the progression of the Euro exchange rate. It is a lessening of the positive effect exercised by a rise in the country’s production, whose public expenditure rises on the exportation of the other country.These effects are expressed by the following equations with positive parameters (a1) and (b1): 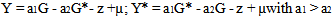 | (2) |
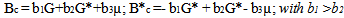 | (3) |
The use of these same parameters a1, a2, b1, b2 in relationships (2) and (3) interprets the hypothesis of symmetry between the two prices. The largest (z) and (µ) respectively represent a symmetric shock to supply that hits the two countries in the same way, and an asymmetric shock in demand that corresponds with a shift in expenditure by the other country.
3. Non co-operative Strategies and Non co-operative Equilibrium with a Shock to Supply
The authorities of the individual countries react to the shocks in supply and on demand with actions on the budget’s policies, which can bring various forms of non co-operative equilibrium of which the first example is Nash Equilibrium[3]. In the case of shocks to supply (z > 0, µ = 0) that hit both Italy and France simultaneously and in the same measure (symmetric shock), the budget’s governance in each country determine the strategy which they consider to be the best, taking into consideration that which the other is putting into action.Therefore, the authorities of the two countries minimise their respective losses defined in (1), taking into account relations (2) and (3) that define their constraints. These constraints derive from the first order conditions of this optimisation (∂Π/∂G = 0, ∂Π*/∂G* = 0) the following functions of the respective reactions to achieve the revenue’s identical objectives (Y* = Yº):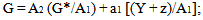 | (4) |
with A1 = a1² + k b1² and with A2 = a1a2 + k b1 b2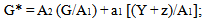 | (5) |
The solution of the system formed by (4) and by (5), allows us to determine the following values of public expenditure that correspond with the Nash Equilibrium.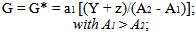 | (6) |
It is possible to represent, in Graphic 1, the functions of reactions (4) and (5) in the line R and R’ for Italy and R* and R*’ for France, in absence (z = 0) or presence (z > 0) of a shock to supply. 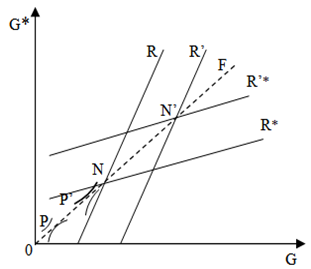 | Graphic 1. Effects of a shock to supply |
The intersection N of the lines R and R* represents the Nash Equilibrium, defined for null shocks and corresponding with the combination of expenditure determined by the relation (6) for z = 0. In N, no governance believes it will be able to obtain better results, taking into account the strategy of the other, considered a given point. A shock to supply (z > 0) is translated in a shift of lines R and R* in R’ and R*’ and in the definition of a new Nash equilibrium (N’), through more significant levels of expenditure defined by (6). In effect, this pressures the budget’s governance to correct the negative effects of the global product. However this correction is only partial. Furthermore, it determines commercial deficit of Italy and France toward the rest of the world. These effects can be measured algebraically on the basis of relationships (2) and (3) in integration of (6).
4. Non-cooperative Equilibrium with a Shock to Demand
The reactions of the budget in Italy and France and asymmetric shocks from the demand side are not prior-determinable. In effect, a shock (µ > 0), which brings about a growth in the global product in Italy and a reduction in France, pushes the Italian budget’s governance to reduce public expenditure and that of France to increase it. But these reactions increase the effects of the shock on these sales and push the authorities to increase the expenditure in Italy and to reduce it in France. On the basis of this relative importance of the model’s parameters, either one of the reactions prevails, as shown in the comparison of following values of expenditure in the presence of a shock (µ > 0), or in absence µ = 0):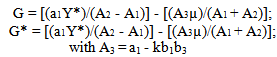 | (7) |
Relationship (7) is deduced from the functions of reactions of the two countries that result from the minimization of the losses defined in (1), under constraints (2) and (3) specified by z = 0 e µ > 0.If the value of A3 is positive, the shock in demand determines, (in graphic 1) the shift of R and of R* towards the top. The new Nash equilibrium, which is shown at a point on the high right, compared with N, shows Italian public expenditure, which is less significant than N and more significant to French public expenditure.The shock induces opposite effects in the case in which the value A3 is negative. However, the reactions of the Italian authorities determine a rise in production and a commercial surplus in Italy and they have opposite effects in France. These effects can be measured on the basis of relationships (2) and (3) in integration as in (7).
5. Coordination of Budget Policies
Coordinating the budget policies presents the possibility of exploiting the relations of interdependency between European countries to maximise the wellbeing of the EMU or to minimise the losses owed to the shocks[4]. Hence, coordination corresponds with the concept of cooperation present in Games theory. The budget’s cooperative strategies are analysed below, in the cases of shocks, and their effects will be compared to those derived from non-cooperative strategies.In the first hypothesis we look at a shock to supply. If Italy and France should find themselves facing a mutual shock to supply and they decide to cooperate, they must coordinate to fix a level of public expenditure that minimises the considered sum of their losses (Π) and (Π*). The latter two are defined by the values z = 0 and µ = 0 through the relations that compare expression (1) and that include constraints (2) and (3). These have the same weight because the two countries are symmetric. From the first order conditions in this minimisation, a system of two relationships can be derived between (G) and (G*). This solution allows us to define public expenditure in line with the cooperative solution: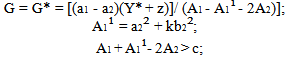 | (8) |
On the basis of (8), a shock to supply happening to a cooperative equilibrium, there is a rise in public expenditure in the two countries. A comparison between relationships (6) and (7) shows evidence that public expenditure in the absence of shock (z = 0) and its increase induced by a shock (z > 0) can be more or less elevated in cooperative equilibrium, compared to Nash equilibrium.This indeterminate outcome derives from two different external factors, linked to the policies of the budget, that are overlooked by the non-cooperative strategies, however accounted for in the cooperative strategies:1) The expansion of the budget, provoked by the shock to supply in any country, increases the losses of the other by reducing the current value of its global product which is assumed inferior;2) The expansion of the budget of any country improves commercial balance; this lessens its negative effect on national budget. Taking into account these reciprocal effects, the cooperative solution suggests a more significant rise in public expenditure compared to when there is an absence of coordination.The first prevails over the second if the value of b2 is weak. In this case, the cooperative equilibrium, represented by graphic 1 from point P, corresponds with less elevated public spending, less elevated to that of the Nash equilibrium.Point P is situated on the bisector (0F) because the two countries are symmetric. Furthermore it is placed on the exchange curve formed by the points of tangency of the two iso-losses curve. The latter forms an ellipse and indicates all the combinations of G and G* that ensure the same level of losses. The effects of the shock to supply on public expenditure results in a shift from N to N’ in the absence of cooperation, and in a less significant shift of P into P’ in the case of a cooperative agreement which allows the internalisation of externalities resulting from the measures’ to the budget’s policies. In fact the deviation of the global product in relation to its desired value is more marked and the commercial deficit less relevant in the presence of coordination compared to when there is an absence of it.In the hypothesis in which the value of b2 is elevated, point P is situated to the right of N in the absence of a shock, and moves, further, under the effect of a supply shock. In every case the cooperative agreement on the budget’s policies brings an optimal pareto characterised by less significant social losses to those resulting in the presence of independent policies.
6. Shock to Demand and Coordination
If the two European countries cooperate in order to resist a rise in the demand for goods in Italy to the negative effect on the demand in France, they fix the following levels of direct public spending to minimise the sum of their losses illustrated by (1), taking into account the constraints of (2) and (3):G = [(a1 - a2 )Y*]/(A1 - A1¹ - 2A2) - [(A3 + A3¹)µ/(A1 - A1¹- 2A2)];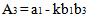 | (9) |
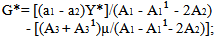 | (10) |
On the basis of (9) and of (10), the sense of variation in public spending derived from the shock to demand, in the two countries, depends on the resulting sign from the sum (A3 + A3¹). Furthermore, comparing (9) and (10) with relationship (7), defined by z = 0, one can ascertain how these variations can be more or less important in the presence of a coordination agreement rather than in the absence of one. This last indeterminate issue, derives, as in the case of a shock to supply, from the importance of the externality which bears heavily on global products and commercial balances. Just as in the case of a weak externality on commercial balances (b2 weak), the contraction of the budget in Italy and the expansion in France are more significant if they derive from a coordinated approach as opposed to isolated and independent decisions.In effect, the cooperative policies internalise the effects of stabilising the variation in public expenditure of any country in the global product of the other; this cannot happen in Nash equilibrium.
7. Conclusions
Ultimately, this policy has a more favourable effect on commercial balances compared to non-cooperative activity. However, the cooperative reactions by the budget’s governance to shocks in demand result anyway in less significant losses as opposed to non coordinated policies. Furthermore, the cooperative equilibrium obtained like this, gives the place optimal pareto.The analysis of the budget strategies in the absence and in the presence of a symmetric shock to supply and a consequential asymmetric shock to demand, shows that:1) In a model of two countries, the cooperative solutions are superior to non-cooperative solutions[5];2) The needs of flexibility in budget policies used in order resist the shocks, depending on the nature of the chosen strategies, from the origin of shock to the relative significance of the externality.
ACKNOWLEDGEMENTS
The author would like to thank the anonymous referee for helpful comments and precious suggestions.
Notes
1. Bryson J. H. (1994), pp. 307-326.2. For a deeper understanding of this concept see: Beetsma R. and Bovenberg A. L. (1998); Cooper R. and Kempf H. (2000); Dixit A. and Lambertini L. (2001). 3. Nash J. (1951), pp. 286-295.4. For a deeper understanding of the coordination models in economics policy see: Bensaid J. and Gravel F. (1993), pp. 50-53; Muet P. A. (1995).5. Even if cooperative solutions result in being superior, these may still encounter difficulties, Frankel J. A. (1987); Frankel J. A. and Rockett K. (1988), pp. 318-340.
References
| [1] | Artus P. (1997), Pacte de stabilité ou control du tax d’endettement public, CDS, pp. 35-58. |
| [2] | Beetsma R. and Bovenberg A. L. (1998), “Monetary union without fiscal coordination may discipline policymakers”, Journal of International Economics, n. 45, pp. 239-258. |
| [3] | Bensaid J. and Gravel F. (1993), “UEM et Coordination des Politiques Budgétaires”, Economie et Prévision, n. 109, pp. 50-53. |
| [4] | Bryson J. H. (1994), “Macroeconomic stabilization through monetary and fiscal policy coordination”, Open Economic Review, vol. 5, n. 4, pp. 307-326. |
| [5] | Cabral A. (2001), “Main aspect of the working of the SGP”, in Brunila A., Buti M. and Franco D. (edited by), The stability and Growth Path, Basingstoke, Palgrave, pp. 139-157. |
| [6] | Cooper R. and Kempf H. (2000), “Designing stabilization policies in a monetary union”, Working Paper, n. 7607, NBER Cambridge. |
| [7] | Dixit A. and Lambertini L. (2001), “Monetary and fiscal policy interactions and commitment versus discretion in a monetary union”, European Economic Review, n. 45, 4-6, pp. 977-987. |
| [8] | Frankel J. A. (1987), “Obstacles to international macroeconomic policy coordination” International Monetary Fund, Working Papers, n. 87. |
| [9] | Frankel J. A. and Rockett K. (1988), “International macroeconomic policy coordination when policy makers do not agree on the true model”, The American Economic Review, vol. 78, n. 3, pp. 318-340. |
| [10] | Muet P. A. (1995), “Adjustment macroeconomiques, stabilization et coordination en Union monétaire”, Revue d’économique politique, n. 105. |
| [11] | Nash J. (1951), “Non-cooperative games”, Annals of Mathematics, 54, pp. 286-295. |

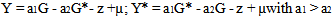
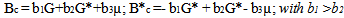
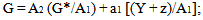
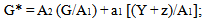
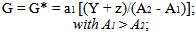

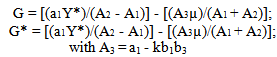
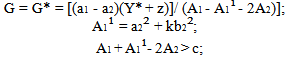
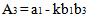
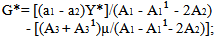
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML