-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
p-ISSN: 2325-0046 e-ISSN: 2325-0054
2012; 1(5): 43-47
doi: 10.5923/j.jgt.20120105.04
Repeated Time Allocation of National and Private Sector by Real Estate Agent
Prakash Chandra1, K. C. Sharma2
1Deptt. of Applied Science & Humanities, Dronacharya College of Engineering, Gurgaon, India
2Deptt. of Mathematics and Computer Science, MSJ Govt. College, Bharatpur, Rajasthan, India
Correspondence to: Prakash Chandra, Deptt. of Applied Science & Humanities, Dronacharya College of Engineering, Gurgaon, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents the time (real estate agent (broker)’s service hours) - allocation of two types of firms’ product (national (leader)-firm and private (follower)-firm) repeatedly. Where the strategy of the national (leader) firm is to decide the product whole sale price and the private developer plays a role of the follower with respect to maximize its payoff. We characterize the resulting Stackelberg equilibrium in terms of time allocation to these developers as well as price with the parameters. A real estate agent controls the service hours which is taken in the normal form. In this game theoretic model, quality of the product is measured by baseline sales, brand substitution degree and price positioning. Future research through simulating this model can show many more application results.
Keywords: Stackelberg Model, Repeated Game Theory, Nash Equilibrium
Cite this paper: Prakash Chandra, K. C. Sharma, "Repeated Time Allocation of National and Private Sector by Real Estate Agent", Journal of Game Theory, Vol. 1 No. 5, 2012, pp. 43-47. doi: 10.5923/j.jgt.20120105.04.
Article Outline
1. Introduction
1.1. Players’ Role
- Real estate agent (Broker) has crucial role in the production of the real estate product and their sale, for that he serves by serving in the allowed time period( Efficient hours of the service) which is limited resource that must be optimally divided among the different categories and their various real estate developer’ product (Shops, Houses). Here, the issue of time-allocation and impact on agent’s performance has attracted the attention of game theorist for preparing the model to solve the problem. National developer of the real estate (Leader-firm) and Private developer of the real estate (follower-firm) are distinct due to having some basic economic ability to produce a wide range of outputs with reasonable profit margin and their size. We can distinct the leader and follower by emerging in industries comprised of some well established firms with sound assets, and other newer, more fragile firm. The follower firms, being less resilient to business shocks, may hence adopt a follower role in the market, awaiting for the more established leader firms to stabilize before making decisions on their own production levels. Undoubtedly, obtained equilibrium solution is a fixed point of the dynamic process in which the leader-and follower-firms readjust output levels according to the strategic market assumptions.
1.2. Equilibrium Literature
- Literature of the model is not wide, the classical Stackelberg game (Stackelberg 1934) models competition in a duopoly market composed of one leader and one follower. Real estate national developer (leader) makes its decision taking into account the reaction of the follower. Literature can be divided in three sections which we have used to place in this game theoretic model. One is Stackelberg model in which one firm works in the model as a leader firm and other firm works as a follower to optimize. Second is the time allocation, which is quite empirical in nature, has indeed a positive impact. Third is equilibrium of this model in repeated interaction of the real estate agent with national developer in a noncooperative game. We have managed the paper in four sections: in the first section of the paper, introduction of the game theoretic model is presented which carries more supportive explanation of the national developer of the real estate (leader-firm) and private developer of the real estate. In second section, Game theoretic model is presented with its assumptions and considering some parameters. In third section some expected results in repeated game move to perfect equilibria. In the last section, we have concluded the agent’s strategy and national developer of the real estate’s strategy.
2. Game Theoretic Model
2.1. Formation of the Game
- Here we have considered a real estate agent
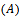 offering two types of product of real estate developers (national (leader) developer and private (follower) developer) within a given product category and its normalize service time in each period of the play. Private developer (follower-firm of real estate)
offering two types of product of real estate developers (national (leader) developer and private (follower) developer) within a given product category and its normalize service time in each period of the play. Private developer (follower-firm of real estate) 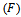 does not play any structural role in this framework. National developer (leader-firm of the real estate)
does not play any structural role in this framework. National developer (leader-firm of the real estate) 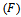 produces and advertises at whole sale price
produces and advertises at whole sale price 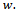 Assumptions: without loss of generality that the agent’s purchasing cost of the private developer’s product is zero. Agent controls the service hours (time) which is taken in normal form. Allocation of time,
Assumptions: without loss of generality that the agent’s purchasing cost of the private developer’s product is zero. Agent controls the service hours (time) which is taken in normal form. Allocation of time, 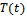 for the national developer’s product and
for the national developer’s product and 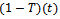 for the private developer’s product to real estate agent, its sum of total distribution of time is unity.Demand for each real estate developer depends on price of each brand and on the exposure each receives, as measured by agent’s service time.Considering factor of the model:1. Agent’s service time allocation, Time
for the private developer’s product to real estate agent, its sum of total distribution of time is unity.Demand for each real estate developer depends on price of each brand and on the exposure each receives, as measured by agent’s service time.Considering factor of the model:1. Agent’s service time allocation, Time 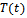 for national developer
for national developer 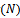 and
and 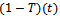 for private developer
for private developer 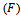 .2. Baseline sales (or brand equity)
.2. Baseline sales (or brand equity) 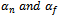 of the national developer and private developer respectively and
of the national developer and private developer respectively and 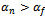 ,
,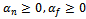 .3. Cross price parameters are at most equal to direct price effects which are
.3. Cross price parameters are at most equal to direct price effects which are 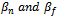 of the national developer and private developer respectively and
of the national developer and private developer respectively and 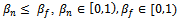 .4. Direct price of the developer
.4. Direct price of the developer 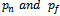 are for the national developer and private developer respectively and
are for the national developer and private developer respectively and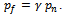 5.
5. 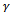 (private developer pricing parameter)
(private developer pricing parameter) 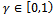 .Demand
.Demand 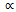 Service Time Allocation by the Real Estate Agent.Each developer’s demand is increasing in competing brand price and decreasing in its own price. These assumptions on effect of pricing are standard. Demand specification indicates that the function is multiplicatively separable into prices and service time allocation to agents of the developer product holder
Service Time Allocation by the Real Estate Agent.Each developer’s demand is increasing in competing brand price and decreasing in its own price. These assumptions on effect of pricing are standard. Demand specification indicates that the function is multiplicatively separable into prices and service time allocation to agents of the developer product holder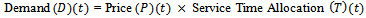
2.2. Inclusion of Parameters in Game
- Service time allocation creates demand which is affected by marginal price. Marginal price effects on demand which depends on the service time allocation to the brand. Demand for each brand depends on the price of each brand and on the time given for exposure.
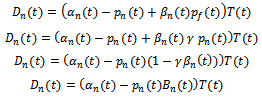 | (1) |
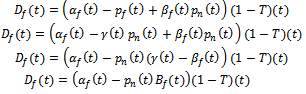 | (2) |
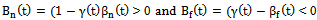 because given empirically established ranges for the cross price effect
because given empirically established ranges for the cross price effect 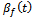 and the private level pricing parameter
and the private level pricing parameter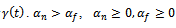 we normalize
we normalize 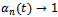 . We further suppose that the agent cannot afford but to national developer, i.e.
. We further suppose that the agent cannot afford but to national developer, i.e. 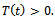 the time constraints
the time constraints 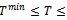
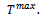 Real estate national developer and real estate agent are profit maximizers, then the payoff function of the national developer
Real estate national developer and real estate agent are profit maximizers, then the payoff function of the national developer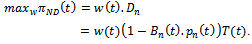 | (3) |
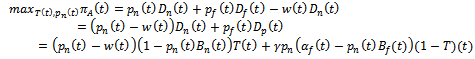 | (4) |
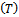 as well as the agent price of the national brand. Then in the next obtained reaction function works for the national developer to decide the optimal whole sale price.
as well as the agent price of the national brand. Then in the next obtained reaction function works for the national developer to decide the optimal whole sale price. 3. Stackelberg Equilibrium
3.1. Reaction Function
- To determine the reaction function of the agent to national developer’s transfer price
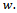
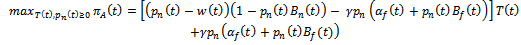 Subject to:
Subject to: 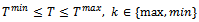 First order optimality conditions are
First order optimality conditions are 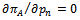
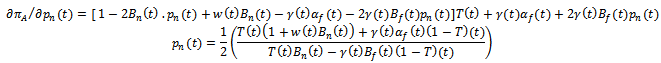 In payoff of function of real estate agent is
In payoff of function of real estate agent is 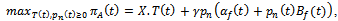 Where
Where 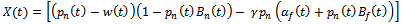 and
and 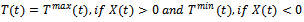 . Then price be max/ min-
. Then price be max/ min-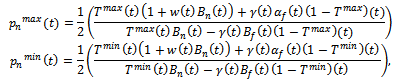
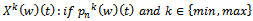 , the reaction function to the national developer’s decision for whole sale price reacts for each period of the game.
, the reaction function to the national developer’s decision for whole sale price reacts for each period of the game.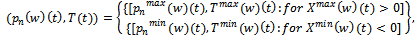 Therefore, we have to consider two cases, depending on whether the time allocation to the national brand of real estate is at its maximal or minimal in repeated game. Now
Therefore, we have to consider two cases, depending on whether the time allocation to the national brand of real estate is at its maximal or minimal in repeated game. Now 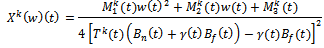 Where
Where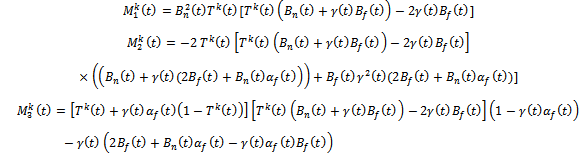
3.2. Equilibrium of the Model
- We get positive
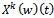 , the time allocation depends on comparative marginal profitability aspect and optimal condition for time allocation can be found with respect to the following results-
, the time allocation depends on comparative marginal profitability aspect and optimal condition for time allocation can be found with respect to the following results-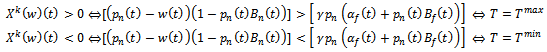 Where
Where 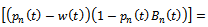 marginal contribution of profit of time allocation to the national developer of real estate and
marginal contribution of profit of time allocation to the national developer of real estate and 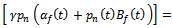 marginal contribution of profit of the time allocation to the private developer of real estate. Hence, we see the time allocation depends on the all the parameters and real estate developers strategy which influence the real estate agent’s time allocation decision.Now for real estate agent’s reaction function, derivate of real estate broker price of national developer brand with respect to the national developer’s whole sale (transfer) price
marginal contribution of profit of the time allocation to the private developer of real estate. Hence, we see the time allocation depends on the all the parameters and real estate developers strategy which influence the real estate agent’s time allocation decision.Now for real estate agent’s reaction function, derivate of real estate broker price of national developer brand with respect to the national developer’s whole sale (transfer) price 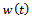
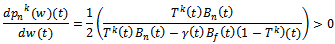 And price relation of the brand is
And price relation of the brand is 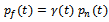 . Then we get
. Then we get 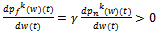 through this we see i) increasing (decreasing) the whole sale price leads to an increasing (decreasing) in the real estate broker price. ii) There is horizontal strategic complement which is a direct consequence of the agent price aspect
through this we see i) increasing (decreasing) the whole sale price leads to an increasing (decreasing) in the real estate broker price. ii) There is horizontal strategic complement which is a direct consequence of the agent price aspect 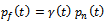 . Real estate National developer’s optimization in each period of the reaped game:
. Real estate National developer’s optimization in each period of the reaped game: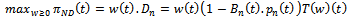 Where
Where 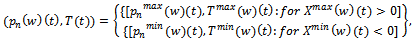 putting for the
putting for the 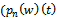 in the national developer’s optimization problem, the first-order condition
in the national developer’s optimization problem, the first-order condition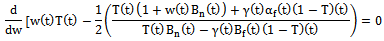 Then
Then 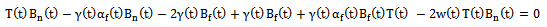 If
If 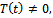 the optimal
the optimal 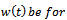 each period of game
each period of game 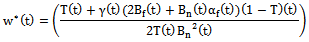 Now substitution above value in the real estate agent’s reaction function, then price strategy of the equilibrium be
Now substitution above value in the real estate agent’s reaction function, then price strategy of the equilibrium be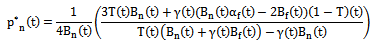 *: for max/min of
*: for max/min of 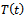 .Equilibrium strategies
.Equilibrium strategies 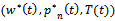 in objective functions of real estate national developer and real estate agent give payoffs
in objective functions of real estate national developer and real estate agent give payoffs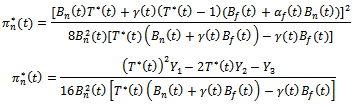 Where
Where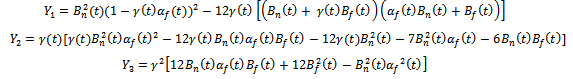 Here we get Stackelberg equilibrium in each period of the game with changes of the different values of the parameters; there is infinite number of the combination to choose the parameters value, for each this combination there is a unique Stackelberg equilibrium.
Here we get Stackelberg equilibrium in each period of the game with changes of the different values of the parameters; there is infinite number of the combination to choose the parameters value, for each this combination there is a unique Stackelberg equilibrium.4. Conclusions
- This paper has a wide scope for further study to get through simulated results that depend on value of the chosen parameters and the future investigation. In this paper, a model is linear to each developer in time allocation and simultaneously tackles pricing strategies and time allocation in the context of private developer and different parameters i.e. brand equity, price-positioning and price substitution in each period of the game. We get parameters result for each combination which tends to Stackelberg equilibrium in repeated game without loss of generality. Further research should compare our finding to those in case of a broker Stackelberg game or Nash game. There may be different study to increase time by moving not to remain as a single agent but a complete broker-firm and more than one real estate developer and private developer with their behavioural study in repeated finitely and infinitely.
ACKNOWLEDGEMENTS
- I would like to thank the editor Mark Green and the anonymous referees for their comments that helped me considerably improve the form and the content of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML