1. Introduction

Hamilton and Slutsky[1] consider the novel issue of endogenous timing in two-player games, with important modeling implications for several models in industrial economics. In a preplay stage, players decide whether to select actions in the basic game at the first opportunity or to wait until they observe their rivals’ first period actions. In one extended game, players first decide when to select actions without committing to actions in the basic game. The equilibrium has a simultaneous play subgame unless payoffs in a sequential play subgame Pareto dominate those payoffs. In another extended game, deciding to select at the first turn requires committing to an action. They show that both sequential play outcomes are the equilibria only in undominated strategies. In addition, Yang et al.[2] compare Bertrand and Cournot equilibria in a differentiated product duopoly under endogenous timing with observable delay, and demonstrate that endogenous timing leads to two sequential play with both leader-follower configurations in Bertrand, but simultaneous play in Cournot. There are many further studies (see, for example,[3-14]). However, these studies are models with profit-maximizing capitalist firms and do not include labor-managed firms.

Therefore, we examine an endogenous timing in labor-managed duopoly competition. The pioneering work on a theoretical model of a labor-managed firm was conducted by[15]. Since then, many economists have studied the behaviors of labor-managed firms (see, for example,[16-31]) (see also[32-35] for excellent surveys).

Lambertini[36] considers a mixed duopoly where a profit-maximizing and a labor-managed firm compete either in prices or in quantities and shows that if firms can choose the timing of moves before competing in the relevant market variable, the Bertrand game yields multiple equilibria, while the Cournot game has a unique subgame perfect equilibrium with the profit-maximizing firm in the leader’s role and the labor-managed firm in the follower’s role. Lambertini[36] considers mixed market competition with profit-maximizing and labor-managed firms, while we investigate pure market competition with labor-managed firms.

We examine a Cournot model in which two labor-managed firms compete against each other. The game is as follows. Each labor-managed firm must choose output either in period one or in period two. If the labor-managed firms decide to choose output in the same period, a simultaneously move game occurs, whereas if the labor-managed firms decide to choose output in different periods, a sequential move game arises.

The purpose of this study is to present the equilibrium of endogenous timing Cournot competition where two labor-managed firms compete against each other.

The remainder of this paper is organized as follows. In Section 2, we describe the model. In Section 3, we discuss the equilibrium of the model. Finally, Section 4 concludes the paper.

2. The Model

Let us consider a market with two labor-managed firms, firm A and firm B. In the remainder of this paper, subscripts A and B denote firm A and firm B, respectively. In addition, when i and j are used to refer to firms in an expression, they should be understand to refer to A and B with 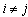. The market price is determined by the inverse demand function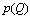, where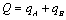. We assume that 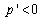and 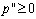. This assumption includes linear and constant elasticity demand functions such as 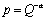, 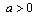.¹

Firm i’s income per worker is given by

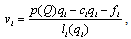(1)

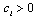where denotes firm i’s capital cost for each unit of output, 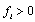is firm i’s fixed cost, and 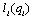is the number of workers in firm i. We assume that 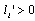and 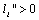. Each firm chooses 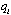in order to maximize (1).

The timing of the game is as follows. In period 0, each firm simultaneously and independently chooses 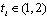, where 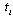indicates when to decide the non-negative output 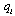. That is, 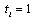implies that firm i decides in period 1, and 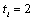implies that it decides in period 2. At the end of period 0, each firm observes 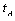and 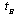. In period 1, firm i choosing 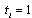selects its output 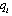in this period. In period 2, firm i choosing 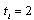selects its output 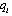in this period. At the end of the game, the market opens and each firm sells its output .

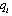3. Equilibrium

In this section, we discuss the equilibrium of the model described in the previous section. We use subgame perfection as the equilibrium concept. We restrict our attention to pure strategy equilibria.

First, we derive the reaction functions in quantities. The equilibrium occurs where each firm maximizes its objective with respect to its own output level, given the output level of its rival. Firm i’s reaction function is defined by

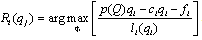(2)

We now present the following lemma.

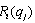Lemma 1. Under Cournot competition, is upward sloping.

Proof. Firm i aims to maximize its income per worker with respect to its own output level, given the output level of firm j. The equilibrium must satisfy the following conditions: The first-order condition for firm i is

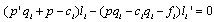(3)

and the second-order condition for firm i is

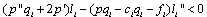(4)

Furthermore, we have

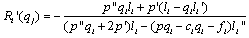(5)

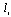Since is a function of 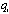and 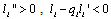, so that 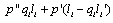is positive. Q.E.D.

Both firms’ reaction curves are drawn in Figure 1, where 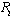is firm i’s reaction curve. Both firms’ reaction curves are upward sloping. This means that both firms treat quantities as strategic complements². The reaction curves cross twice; that is, there are two Cournot equilibria. Only point C is a stable Cournot equilibrium, since in point D firm B’s reaction curve crosses firm A’s from above³. It is clear that each firm’s income per worker is higher at C than at D. In the remainder of this paper, we will not consider the unstable Cournot equilibrium D.

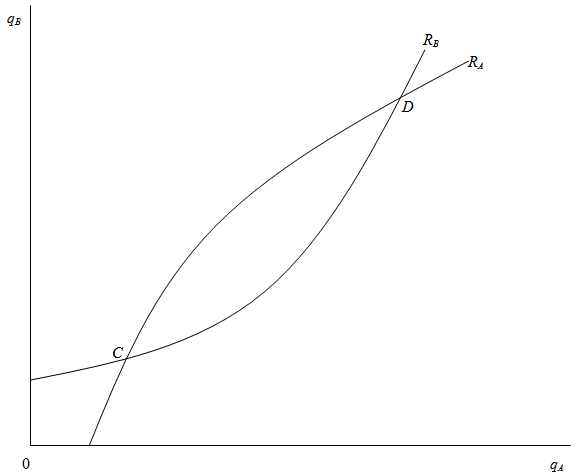Figure 1. Reaction curves in quantity space

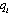Next, we consider Stackelberg games. If firm i is the Stackelberg leader, then firm i selects , and firm j selects 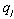after observing 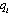. Firm i maximizes 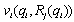with respect to 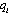We present the following two lemmas, where the superscripts L, F, and C denote the Stackelberg leader outcome, the Stackelberg follower outcome, and the Cournot-Nash outcome, respectively.

Lemma 2. (i) 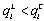and (ii) .

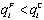Proof. (i) If firm i is the Stackelberg leader, then it maximizes 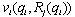with respect to 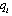. Therefore, firm i’s Stackelberg leader output satisfies the first-order condition:

Lemma 1 states that 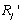is positive. Since 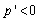and 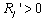, 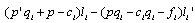must be positive to satisfy (6).

(ii) Lemma 1 shows that 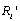is strictly positive. Lemma 2 (i) means that firm j’s Stackelberg leader output is smaller than its Cournot output. Thus Lemma 2 (ii) follows. Q.E.D.

Lemma 3. (i) 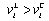and (ii) .

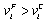Proof. (i) Since the Stackelberg leader maximizes its income per worker and can choose 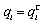, we obtain 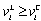. Lemma 2 (i) states 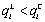. Thus Lemma 3 (i) is derived.

(ii) Since 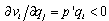, decreasing 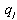increases 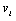given 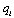, and thus Lemma 3 (ii) follows. Q.E.D.

These lemmas indicate that each firm has an incentive to decrease its output.

We now present the equilibrium of the observable delay game formulated in Section 2.

Proposition 1. The game has two pure-strategy Nash equilibria: (1, 2) with payoffs 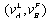and (2, 1) with payoffs .

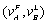Proof. In period 0, each firm simultaneously and independently chooses 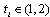. At the end of period 0, each firm observes t_A and t_B. In period 1, firm i choosing 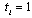selects its output in this period. In period 2, firm i choosing 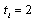selects its output in this period. At the end of the game, the market opens and each firm’s income per worker is decided. Our equilibrium concept is subgame perfection, and all information in the model is common knowledge. Hence, we can consider the following payoff matrix:

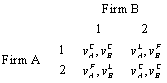Thus, the proposition follows from Lemma 3. Q.E.D.

Proposition 1 means that each firm is either a leader or a follower.

4. Conclusions

We have examined endogenous timing in a Cournot duopoly where two labor-managed firms compete against each other. There are two production periods, and the labor-managed firms simultaneously and independently announce in which period they will choose their outputs. If the labor-managed firms decide to choose output in the same period, a simultaneously move game occurs, whereas if the labor-managed firms decide to choose output in different periods, a sequential move game arises. We have shown that there is no equilibrium where the labor-managed firms choose output in the same period. As a result, we have found that each firm may play the role of Stackelberg leader.

Notes

1. See, for example,[37].

2. The concept of strategic complements is introduced by[38].

3. For this point, see[26].