-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Game Theory
2012; 1(3): 10-14
doi: 10.5923/j.jgt.20120103.02
The Shape of Payoff Functions in N-person Games
Miklos N. Szilagyi, Iren Somogyi
Department of Electrical & Computer Engineering University of Arizona, AZ 85721, Tucson
Correspondence to: Miklos N. Szilagyi, Department of Electrical & Computer Engineering University of Arizona, AZ 85721, Tucson.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We report computer simulation experiments based on our agent-based simulation tool to model an N-person game for the case when the agents are greedy simpletons who imitate the action of that of their neighbors who received the highest payoff for its previous action. The individual agents may cooperate with each other for the collective interest or may defect, i.e., pursue their selfish interests only. After a certain number of iterations the proportion of cooperators stabilizes to either a constant value or oscillates around such a value. The payoff (reward/penalty) functions are usually given as two straight lines: one for the cooperators and another for the defectors. The payoff curves are functions of the ratio of cooperators to the total number of agents. Even for linear payoff functions we have four free parameters that determine the payoff functions. In real-life situations, however, the payoff functions are seldom linear. In this short note we will show the influence of their shape on the results of the simulations. The defectors’ payoff function will still be linear but parabolas will represent that of the cooperators.We investigated the influence of the shape of the cooperation payoff function by running a large number of simulations. The results show that the solutions of N-person games with quadratic cooperation functions have some predictable tendencies but they are non-trivial and quite irregular with sharp fluctuations in certain regions. The solutions show drastic changes in some very narrow parameter ranges. The shapes of the payoff functions have a profound influence on the outcome of the games.
Keywords: Agent-based Simulation, Cooperation, N-person Games
1. Introduction
- N-person games have been investigated by computer simulation under the assumption that the payoff functions are linear [1-4]. In real-life situations, however, the payoff functions are seldom linear [5]. For example, we have simulated a new game with parabolic payoff functions [6]. In this short note we will show the influence of their shape on the results of the simulations. The defectors’ payoff function will still be linear but parabolas will represent that of the cooperators. New papers about N-person games (for example, [7]) do not consider this problem at all. Agent-based simulation will be presented for the case when the agents are greedy simpletons who imitate the action of that of their neighbors who received the highest payoff for its previous action.
2. The Model
- The individual agents may cooperate with each other for the collective interest or may defect, i. e., pursue their selfishinterests. Their decisions to cooperate or defect will accumulate over time to produce a result that will determine the success or failure of the given artificial society.As usual, the payoff functions will be presented as functions of the number of cooperators related to the total number of agents (x). The payoff to each agent depends on its choice and on the distribution of other players among cooperators and defectors. We will assume that the payoff functions D(x) for the defectors are linear functions of this ratio x, but those for cooperators C(x) are quadratic. The two functions cross each other at a certain value of xcross. The payoff function C(x) is the same for all cooperators and D(x) is the same for all defectors (uniform game). We will use our agent-based model developed for simulated social and economic experiments with a large number of decision-makers operating in a stochastic environment [8]. The simulation environment is a two-dimensional array of the participating agents. Its size is limited only by the computer’s virtual memory. The behavior of a few million interacting agents can easily be observed on the computer’s screen. There are two actions available to each agent, and each agent must choose between them (cooperation or defection). The cooperators and the defectors are initially distributed randomly over the array. In the iterative game the aggregate cooperation proportion changes in time, i.e., over subsequent iterations. At each iteration, every agent chooses an action according to the rewards to its neighbors. The software tool draws the array of agents in a window on the computer’s screen, with each agent in the array colored according to its most recent action. The updating occurs simultaneously for all agents.After a certain number of iterations the proportion of cooperators stabilizes to either a constant value or oscillates around such a value. The experimenter can view and record the evolution of the society of agents as it changes in time. The outcome of the game strongly depends on the “personalities” of the agents, i.e. e. on the type of their responses to their environment. The software tool allows for a number of different personalities and their arbitrary combinations. In this work we assume that all agents are greedy simpletons.
3. Simulation
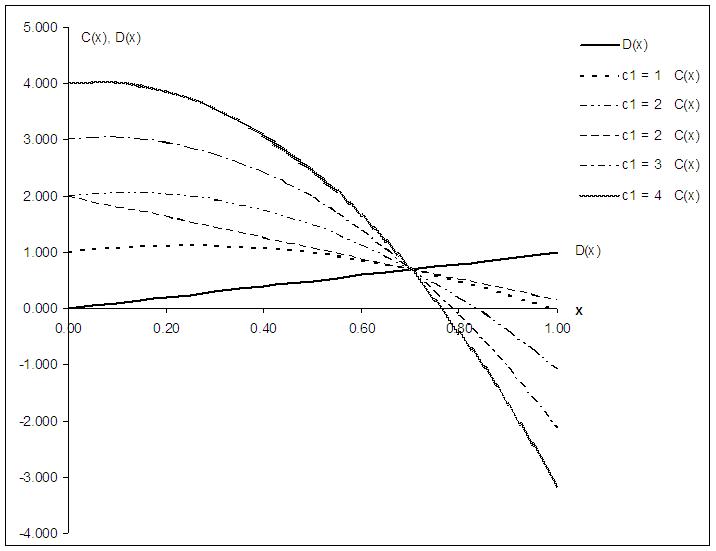
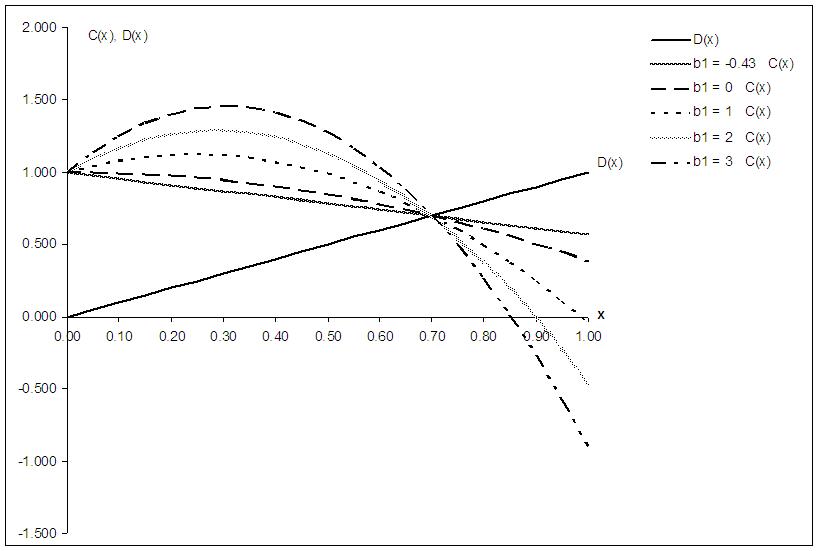
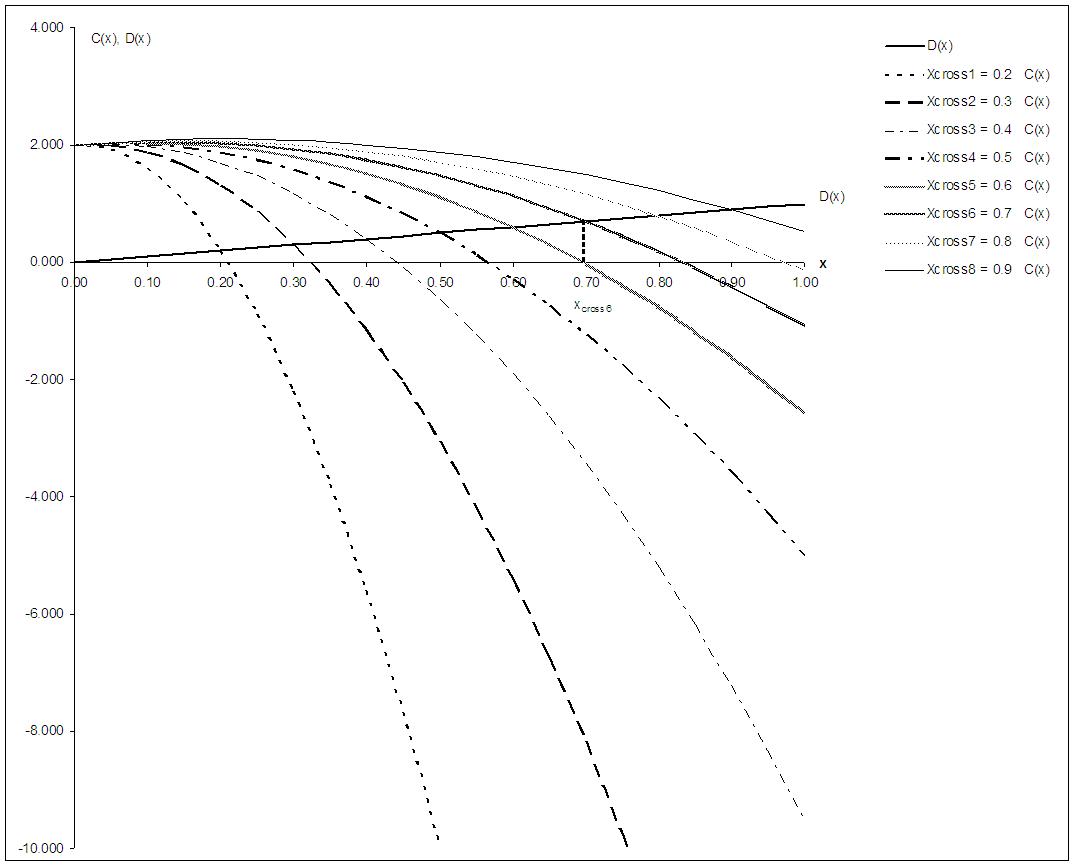
- Throughout this work the total number of agents is 500x500=250,000, the initial ratio of cooperators is 50% and the neighborhood of each agent is one layer deep, i.e., each agent has exactly eight neighbors except those that are situated at the borders of the array.We represent the payoff functions as
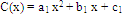 | (1) |
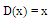 | (2) |
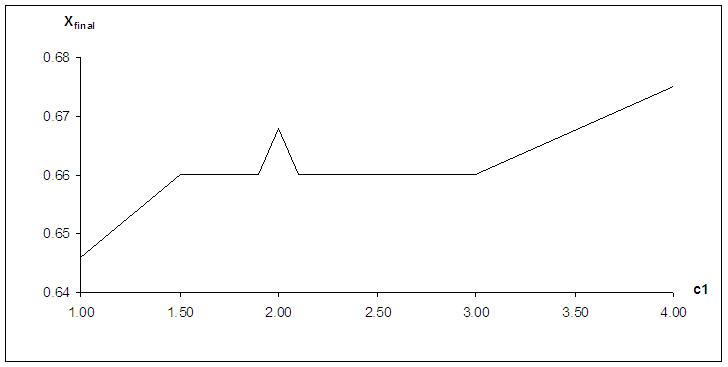 | Figure 2. The solution of the game Xfinal as a function of c1 |
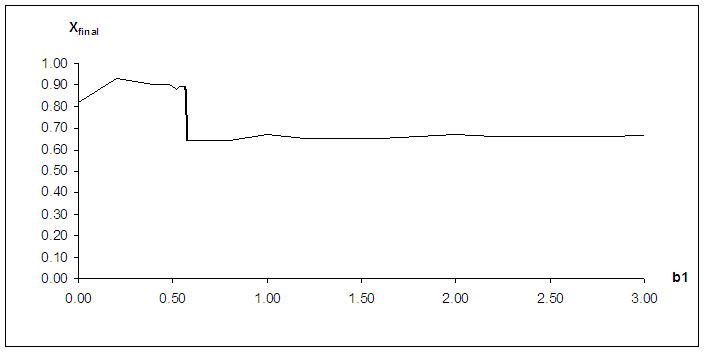 | Figure 4. The solution of the game Xfinal as a function of b1 |
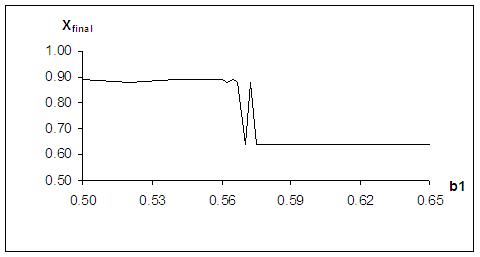 | Figure 5. Refined solution: Xfinal around b1 = 0.57 |
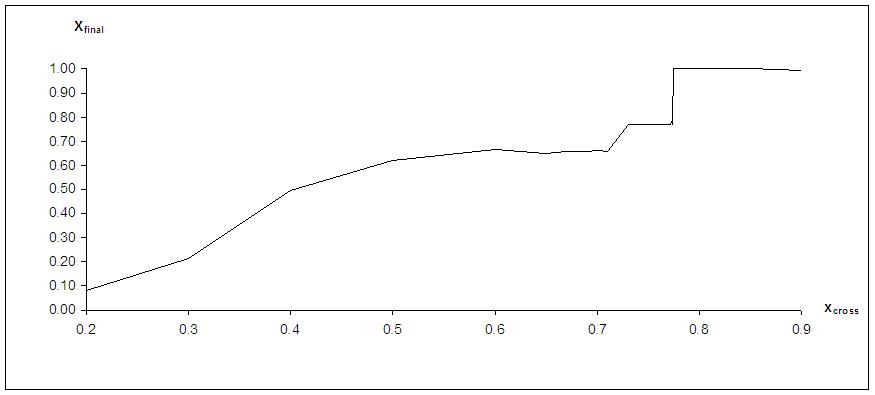 | Figure 7. The solution of the game Xfinal as a function of xcross |
4. Conclusions
- Our simulations show that the shapes of the payoff functions have a profound influence on the outcome of the games in most cases. The solutions of N-person games with quadratic cooperation functions show drastic changes in some very narrow parameter ranges. The explanation of this phenomenon would require a thorough mathematical analysis of N-person games, which is not yet available in the literature. Further simulations of N-person games may also lead to their better understanding.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML