-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2023; 13(1): 24-32
doi:10.5923/j.jce.20231301.03
Received: Jun. 2, 2023; Accepted: Jun. 23, 2023; Published: Jun. 26, 2023

Theoretical Prediction of the Ultimate Shear Resistance of Thin-Walled Stainless Steel Plates
Ian T. Otwani
Department of Civil, Construction and Environmental Engineering, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya
Correspondence to: Ian T. Otwani, Department of Civil, Construction and Environmental Engineering, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The study investigated the theoretical prediction of the ultimate shear resistance of thin-walled stainless steel plates. Available experimental data from various literature, 34 in number, were gathered and examined in terms of structural performance when subjected to shear loads. Comparisons were conducted between theoretical and experimental ultimate shear resistance predictions. Evaluation of present design methods such as Eurocode 3: Part 1-4, Eurocode 3: Part 1- 5 and recent proposals was conducted, and disparities were identified. From the evaluation, it was deduced that there were some overestimations and failures to meet specific provisions provided in Eurocode 3: Part 1-4 and Eurocode 3: Part 1- 5. Thus a proposed method sufficed in drawing a correlation between the theoretical predictions and the experimental data using a multiple linear regression model. The proposed method's ultimate shear resistance predictions were compared with the theoretical predictions and experimental data using statistical analysis. Through a reliability analysis, the proposed method better predicted the ultimate shear resistance of the stainless steel thin-walled plate girders by closely examining the coefficient of determination, R2 and the relative closeness of the predicted values to the experimental values.
Keywords: Dependent variable, Experimental results, Independent Variable, Multiple Regression, Plate Girders, Reliability Analysis, Shear resistance, Stainless steel
Cite this paper: Ian T. Otwani, Theoretical Prediction of the Ultimate Shear Resistance of Thin-Walled Stainless Steel Plates, Journal of Civil Engineering Research, Vol. 13 No. 1, 2023, pp. 24-32. doi: 10.5923/j.jce.20231301.03.
Article Outline
1. Introduction
- Thin-walled steel plate girders are frequently utilised in various ways in structural engineering due to their underlying strength-to-weight ratio that is considerably high, as well as the stiffness and strength post-buckling reserve [1]. For an applied bending moment, the axial forces in the girders’ flanges decrease with an increase in the web depth (h); therefore, it is imperative to have a web with sufficient depth [2]. Induced shearing stresses on a plater girder’s practical length are relatively lower than the flexural stresses on the flanges. Thus, web panels can buckle at relatively low shear loading. Consequently, the web panels are typically stiffened vertically to increase buckling strength. The design should be economical in terms of costs and fabrication regarding the selection of web plate thickness and the spacing of stiffeners [3]. The girder's ultimate shear capacity is derived from the following contributions: 1) the flanges' plastic moment capacity, 2) the elastic critical load, and 3) the post-critical membrane tension obtained from formularised tension [4].Various proposals have sufficed over the last century in an attempt to predict the post-buckling shear resistance of thin-walled webs in plate girders based on the action of the tension field [5], which postulates that the post-buckling shear strength source is the tensile stresses developed in a well-defined diagonal field caused after elastic shear buckling [6].The research aims to research the response of stainless steel plate girders to shear, gather and examine the available data on structural performance, review present design methods, develop a multiple regression expression, and verify the expression statistically for suitability for inclusion in the relevant design codes.
2. Literature Review
2.1. Introduction
- The following section outlines the available laboratory examinations on stainless steel plate girders. Also, a review of the present design methods and proposals utilised in examining the shear buckling resistance of plate girders is briefly done. The design methods under consideration are the rotated stress field method and the tension field method.
2.2. Review of Previous Experimental Research
- The first investigations of stainless steel plate girders were the premise of the codified provisions in ENV 1993-1-4 (1996) [7] used to determine the ultimate shear resistance of stainless steel beams. After the promulgation of ENV 1993-1-4 (1996) [7], researchers such as Olsson [8], Estrada et al. [9] and Real et al. [10] conducted experiments highlighting the scarcities of the existing design methodologies. The main aim of each research was to formulate equations capable of predicting concisely the shear resistance of stainless steel plate girders subjected to shear loading. Recently, extensive experiments have been conducted on stainless steel plate girders; Saliba & Gardner [11] conducted a detailed numerical investigation of lean duplex stainless steel plate girders, while Yuan et al. [12] showed the shear behaviour of diagonally stiffened stainless steel plate girders, thus bringing the laboratory data pool to 38.
2.3. Review of Theoretical Models for Shear Buckling Resistance Prediction
- A shear-loaded flat web plate theoretically has principal stresses at 45 degrees angle before elastic buckling occurs [13]. Basler’s Model [14] depends on various assumptions regarding the load path in the web that has buckled after the development of the tension field. Upon provision of out-of-plane flexural stiffness, the emergence of a tension field in the diagonal direction suffices after buckling due to the defined panelization by intermediate stiffeners [13]. Through the assumption that compressive resistance in the orthogonal direction to the tension is lost in the buckled web, Basler deduced that "the stiffener must take the vertical component of the diagonal stresses out of the web at one end and transfer them to its other end" acting as a compression strut amid the chords [14]. Consequently, the flanges are inclined to truss action to solve the loads as chords anchoring the vertical stiffeners [15]. Basler assumed that flange plates were deficient in weak axis flexural stiffness required to provide anchorage between web forces and diagonals. Studies by Lee & Yoo [3,16] demonstrated that direct anchorage of the tension field to the flange is not necessitous in post-buckling tension field action mobilisation. From previous research, White & Barker [5] formulated repetitions of post-buckling models for ultimate shear strength prediction in slender webs. Findings demonstrated that models composed on the premise of the Cardiff approach were more accurate but needed significantly more computation for the prediction of tension field and flanges interaction. Cardiff's models postulate that the tension field is tied up to both the flange and the stiffener. The plastic hinges development at the flange-to-stiffener interface, and the flange at the tension field width edge influences the ultimate post-buckling capacity [13]. Models formulated using Basler's method demonstrated a perfect combination of accuracy and simplicity due to the neglect of flange anchorage.Research by Scandella, Neunschwander, Mosalam, Knoboch, & Fontana [17] on web shear buckling tests on thin-walled plate girders demonstrate similarities with models based on Balser's approach for post-buckling shear capacity. Test results of the researchers deduced that plastic mechanism formation per the present Eurocode/Höglund model mobilised more resistance and shear deformation ductility on the onset of the yielding of the buckled web. More information on the slender web plate girders' shear response is demonstrated in [17].Web shear post-buckling phenomenon in Eurocode 3 Section 5, parts 1-5 [19] is based on Höglund's rotated stress theory. Höglund [18] posited a model on the premise of “rotated stress field theory” in that, the instance shear buckling takes place in an unstiffened plate girder, the resultant web membrane stresses required to be anchored to rigid end post for shear resistance development. The influence of the flanges on the behaviour during post-buckling was initially neglected during the formulation of this model; however, subsequent repetitions would be done to include stiffened girders with tensioned fields spanning flange-to-flange. Thus, a plastic mechanism is developed [13].
3. Present and Proposed Design Methods
- The following section looks at the design methods used for shear buckling resistance assessment of plate girders in Eurocode 3 and the development from the ENV prestandard to the current standard. Stainless steel provisions are the primary focus of the section.
3.1. Stainless Steel Design Requirements of ENV 1993-1-4 (1996) & ENV 1993-1-4 (2006)
- ENV 1993-1-4 (1996) [7] design provisions were based on the requirements posited in ENV 1993-1-1 (1992) [20], with changes to reflect stainless steel nonlinearity. However, various research studies [8,9] indicated that provisions in ENV 1993-1-4 (1996) [7] were rather conservative. Also, the test data quality raised concerns and emphasised the need for flange contribution consideration in shear buckling capacity determination. Olsson [8] conducted experimental and analytical research to advance the developed equations for stainless steel plate girders. The set expressions were based on the rotated stress field method and took up the essential rigour of EN 1993-1-5 (2006) [19] given by the equations (1), (2), and (4) shown below. In EN 1993-1-5 (2006) [19], the ultimate shear resistance is denoted as Vb, Rd and expressed as shown in equation (1) which is the sum of the flange contribution, Vbf, Rd (Equation 2) and the web buckling shearing resistance, Vbw, Rd (Equation 4);
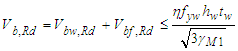 | (1) |
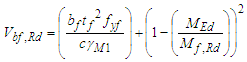 | (2) |
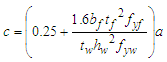 | (3) |
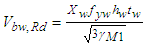 | (4) |
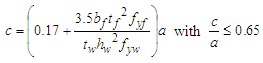 | (5) |
3.2. Proposal by Estrada, Real, & Mirambell (2007)
- Olsson's equations were beneficial compared to the expressions in ENV 1993-1-4 (1996) [7]. Still, the equations did not clearly outline the difference between non-rigid and rigid posts. As a result, Estrada, Real, & Mirambell [9,25] conducted extensive research to identify the efficacy of end post rigidity over a wide range of wen panel slenderness and aspect ratios. Through their findings, proposals were made to revise the design expressions. The proposed expressions retained the rigour of the rotated stress field method, and the shear buckling resistance constituted a flange and web contribution, as shown in equations (1), (2) and (4). The contribution by the flange was similar to the expressions proposed by Olsson [8]; however, the web contribution was revised.Estrada, Real, & Mirambell (2007) [25] proposed varying design equations for web panel aspect ratios greater and less than unity. The latter's consideration was meted on end post rigidity, providing concise test behaviour prediction.
4. Experimental Results
- A summary of the test results from various experiments is tabulated in Table 1 to conduct a comparative analysis of theoretical predictions and test results of the ultimate shear resistance of slender plate girders exposed to shear loads. Table 1 demonstrates the quality of the material, the geometrical dimensions and the ultimate shear resistance results. The geometrical labels and terminology of various parts of the girders tabulated in Table 1 are demonstrated in Figure 1.
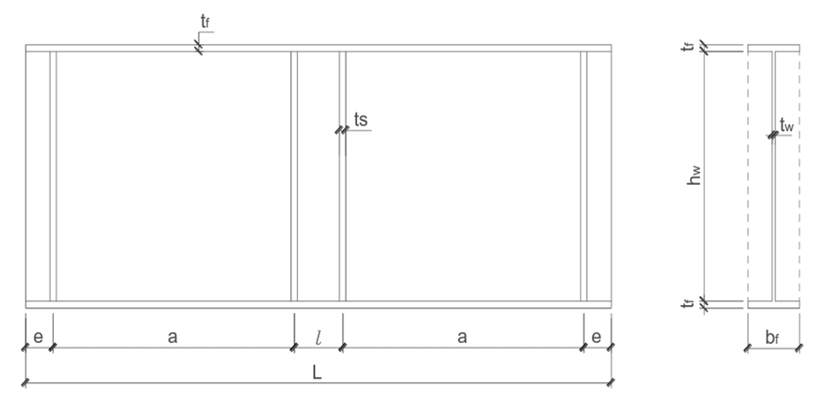 | Figure 1. Geometrical labelling of the plate girder. Source: [26] |
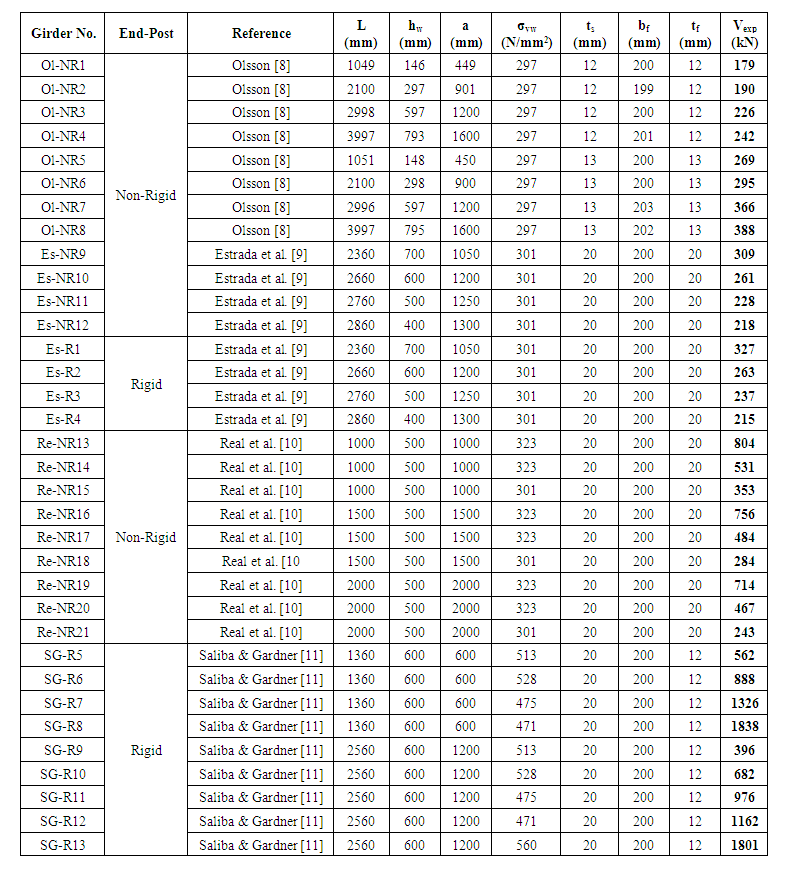 | Table 1. Girders used in various experimental studies |
5. Comparison of Experimental and Theoretical Results
5.1. Introduction
- The following section analyses the results obtained from previous experimental research on stainless steel plate girders to evaluate the provisions stated in section 3. Comparisons are made between the theoretical predictions of Estrada, Real, & Mirambell (2007) [25], EN 1993-1-4 (2006) [24] and EN 1993-1-5 (2006) [19].
5.2. Result Analysis
- The experimental results are first analysed with the design requirements of EN 1993-1-4 (2006) [24]. The design shear resistance, Vc, Rd determination are as set out in the code clause 5.6. An assumption was made that the flange resistance is not fully used to withstand the bending moment. Thus the shear buckling resistance, Xf, was included in the overall shear resistance determination. The predictions were on the premise of measured material characteristics. Parameters such as γm and η were taken as 1.0 and 1.2, respectively; the same applies to the theoretical predictions per EN 1993-1-5 (2006). The expressions provided in EN 1993-1-5 (2006) are similar to the provisions in EN 1993-1-4 (2006), with differences within the coefficients reflecting material response differences. EN 1993-1-5 provides a clear differentiation between non-rigid and rigid plate girders for values of web slenderness greater than or equal to 1.08. Estrada, Real, & Mirambell (2007) [25] proposal adopts the rigour of both EN 1993-1-4 (2006) and EN 1993-1-5 (2006). However, the expressions proposed by Estrada, Real, & Mirambell (2007) [25] differentiate rigid and non-rigid end post plate girders taking into consideration the web panel aspect ratios. Table 2 compares theoretical predictions and test results of the ultimate shear resistance of slender plate girders. The table shows that most of the experimental shear resistance values ratios to the theoretical predictions are less than unity, while some are greater than unity. Ratios with values greater than unity demonstrate failure in design check as provided for in EN 1993-1-5 (2006). A comparison of test results of ultimate shear resistance of slender plate girders and predictions using Estrada, Real, & Mirambell (2007) [25] proposal indicates the low values less than unity as seen in Table 2 hence a demonstration of overestimation. Therefore a new proposal draws a correlation between the theoretical predictions and the test results of the ultimate shear resistance to strike a balance and provide more reliable results about the code provisions.
|
6. Proposed Method
6.1. Introduction
- The following section constitutes the formulation of the proposed methodology that adopts the rigour of the theoretical predictions in section 3. Statistical analysis and a multi-regression expression are proposed to draw a correlation between the predictions and, thus, formulations of an expression following the set provisions that are less conservative.
6.2. Design Proposal
- Statistical analysis is conducted where multiple linear regression analysis is utilised. The regression analysis model statistically analyses the relationship between several independent variables and a dependent variable. The statistical methodology elaborates how a dependent variable adjusts when any one of the independent variables is changed while others are held constant. Based on Estrada, Real, & Mirambell (2007) [25], EN 1993-1-4 (2006) [24] and EN 1993-1-5 (2006) [19], a correlation is made between the theoretical predictions and the experimental results of shear resistance of thin-walled stainless steel plate girders. Table 3 shows the results of the multi-regression analysis, where the experimental shear resistance results are the dependent variables. At the same time, the theoretical predictions are the independent variables, given that any of the variables in the expressions can be varied while others are held constant. As seen in Table 3, the standard error (112.87) is less than the coefficient; thus, the coefficient deduced is statistically significant. The p-value (2.69E-18) of the F-test is lower than 0.05 (95% confidence level); therefore, the null hypothesis is rejected. In an instance where the p-value exceeds 0.05, the regression model is deemed insignificant; that is, the null hypothesis that X variables fail to assist in the prediction of Y is accepted. The model is deemed significant if the p-value does not exceed 0.05 [27].
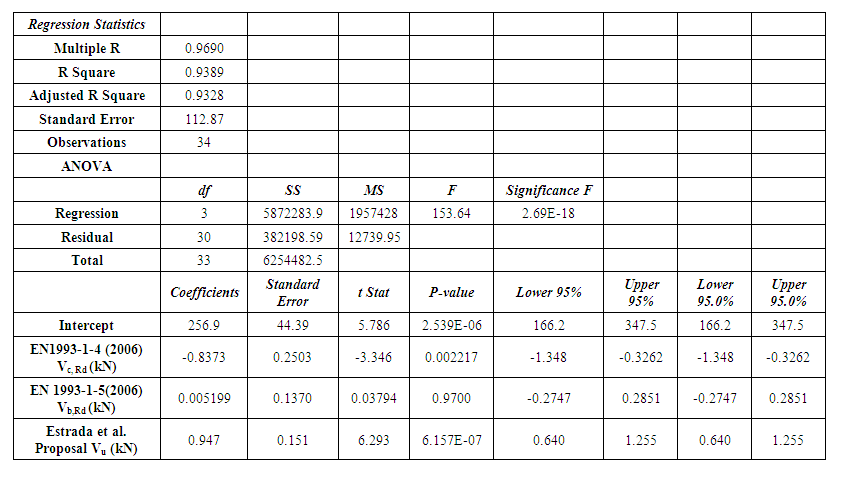 | Table 3. Multiple Linear Regression Analysis of the theoretical predictions and experimental results of shear resistance of thin-walled stainless steel plate girders |
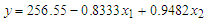 | (6) |
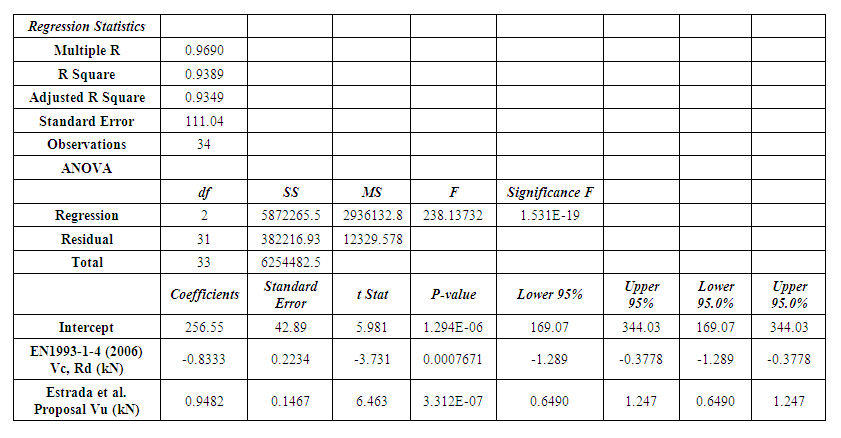 | Table 4. Multiple Linear Regression Analysis of the theoretical predictions and experimental results of shear resistance of thin-walled stainless steel plate girders |
6.3. Reliability Analysis
- The coefficient of determination indicates the data percentage close to the line of best fit. The graph showing R2 is demonstrated in Figure 2. From the analysis in Table 4, it is evident that 93.89% of the data used can be explained through the linear relationship of the proposed method of shear resistance predictions and the independent variables derived from the theoretical predictions of EN 1993-1-4 (2006) and Estrada, Real, & Mirambell (2007) [25] proposal (equation 6). The proposed method thus provides predictions closest to the experimental results of shear resistance (R2= 0.9389) compared to other theoretical predictions (figure 2). Thus the predictive model provides a better tendency of predictability.
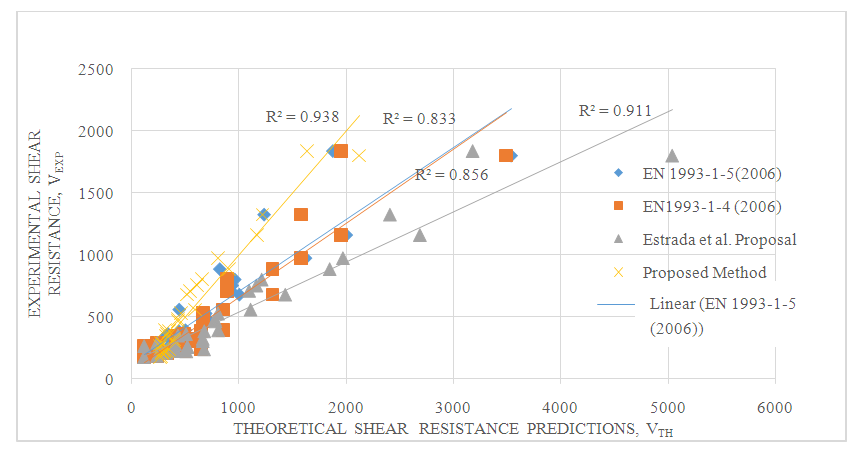 | Figure 2. Comparison of the proposed method to the theoretical predictions for shear resistance |
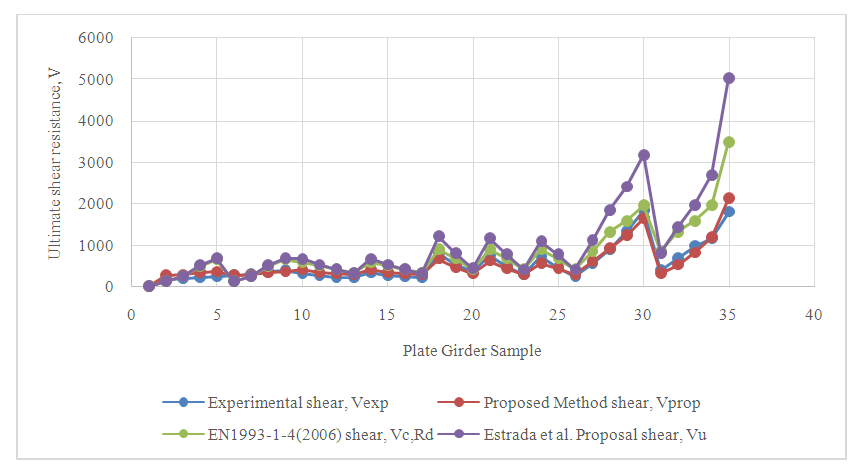 | Figure 3. Comparison of the proposed theoretical and experimental ultimate shear resistance values for various plate girders |
7. Conclusions and Recommendations
- The study sought to investigate the response of stainless steel plate girders to shear, gather and examine available experimental data, and review current design methods. Also, a multi-regression equation model was to be developed, and statistical verification was to assess the suitability of the methods for inclusion in the relevant design codes. Through the literature review, the background of several theoretical predictions was deduced. A total of 34 experimental results were utilised from previous research studies on stainless steel thin-walled plate girders to conduct a comparative analysis with theoretical predictions of Estrada, Real, & Mirambell (2007) [25], EN 1993-1-4 (2006) [24] and EN 1993-1-5 (2006) [19]. It was deduced that some results were unreliable and unsatisfactory to meet the set provisions. Thus, a proposed method that utilises the rigour of the theoretical predictions sufficed. The proposed method was centred on the premise of a multiple regression expression with the independent variables as the EN 1993-1-4 (2006) ultimate shear resistance prediction and Estrada, Real, & Mirambell (2007) [25] proposal prediction. Through reliability analysis, the proposed method was deemed to provide a better predictive tendency of the shear resistance due to the high value of the coefficient of determination R2 and the relative closeness of the predicted values to the experimental values.The study was, however, limited to old data as few studies have been conducted on stainless steel thin-walled plate girders subjected to shear loading; thus, more experimental studies need to be undertaken to test the efficiency of the proposed predictive model. Also, most of the theoretical predictions failed to consider the influence of bending stresses when girders were subjected to shear, thus influencing the predictive model due to their correlation; therefore, further enhancement needs to be carried out in the future with emphasis meted on the influence of bending stresses.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML