1. Introduction

The formation of irregular bed geometry and 3D bedforms is inevitable in natural channels and rivers due to flow regime changes and channel dynamics. The pool–riffle sequences are known as bedforms, which commonly occur in gravel-bed rivers, defined as deeper and shallower parts of the bed, respectively. Generally, riffles are identified as being wider, shallower and coarser than pools [1].

Vegetation is one of the suitable tools for river management, but in the past it was removed from rivers only to consider its effect on flow resistance and to increase flow capacity. Vegetation is a key factor in reducing flow velocity and its presence in floodplains changes flow resistance as well as sediment transport and may affect bedforms. Changes in the wall vegetation characteristics can affect the width and migration rate of the channel as an independent factor and increase the potential capacity to change the river plan [2,3].

Numerous studies have been conducted for evaluating the impact of pool-riffle on low characteristics, sediment transport, and turbulence intensity, including experimental studies, numerical studies, and field investigation [4-12]. Caamano et al. (2006) observed flow jets in different discharges and reported that flow discharge changes affected jet locations [13]. Tokyay and Sinha (2020) showed that the maximum velocity region occurred at the riffle section and decreased towards the pool section. Also, the bed shear stress revealed its maximum and minimum values in the riffle and pool, respectively [8]. Most of the studies on the pool-riffle sequences focused on 2D bed forms. However, morphologically, pools and riffles are inherently three-dimensional and this characteristic needs to be considered in detail in river engineering projects.

Vegetation has a controlling effect on river flow, erosion, and geomorphology. To investigate the effect of vegetation on the flow structure in the laboratory, some researchers used cylindrical objects to simulate the shape of vegetation, and others used natural vegetation [14]. White and Nepf (2007) applied the wooden cylinders as vegetation in the channel floodplain and found that the difference in velocity and the generation of a shear layer between the floodplain and the main channel caused a turning point in the velocity profile [15]. Having used artificial grass and wooden cylinders in a floodplain, McBride et al. (2007) showed that the flow velocity decreased in the presence of cylinders. They claimed that at the border between the main channel and the floodplain, a highly turbulent shear layer formed which intensified in the presence of wooden cylinders [16]. Sun and Shiono (2009) found considerable differences in velocity, shear stress, and discharge in the presence cylinders, compared to experiments without cylinders [17]. Also, vegetation on the walls generated secondary currents causing considerable deviation in the velocity and shear stress distributions [18]. Fazlollahi et al. (2015) found that the presence of wall vegetation intensified the occurrence of maximal velocity under the water surface which was called the dip phenomenon [4].

From the above literature, it is not clear how the interaction of 3D bed forms and wall vegetation may change the flow characteristics, including velocity and shear stress distributions and the validity of log law. These factors significantly influence the estimation of fluvial hydraulic parameters in river restoration projects. The objective of this study is to investigate the effect of 3D bed forms and wall vegetation on the distributions of velocity, shear stress, and shear velocity in a laboratory flume with natural reeds.

2. Experimental Set up

All experiments were conducted in the hydraulics laboratory of the Water Research Institute of the Ministry of Energy. Experiments were carried out in a 13 m long, 0.45 m wide and 0.6 m deep flume with Plexiglas sidewalls (Fig. 1).

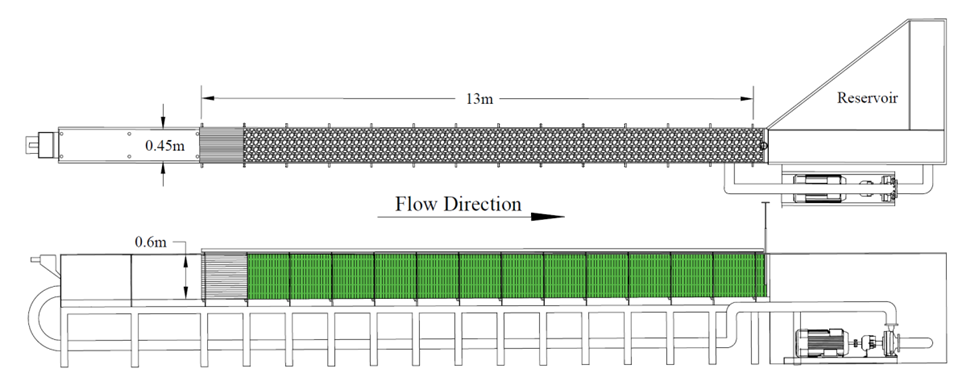Figure 1. Laboratory setup

Due to considerable turbulence in the entrance of the flume, a set of metal panels was used as a filter to help the with energy dissipation of the flow (Fig. 2).

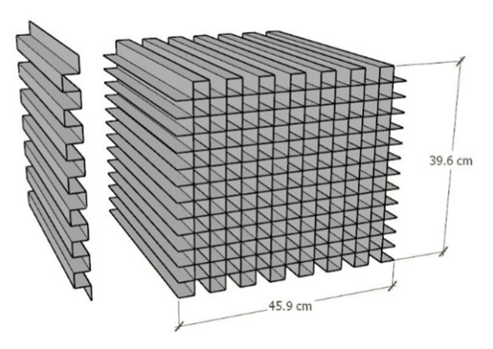Figure 2. Schematic of flow filter

Using field measurements in some reaches in Tireh and Gelroud Rivers in Lorestan Province, in central Iran, and the geometry of bedforms measured by Slotani (2016) and Fazel Najafabadi (2016) in gravel-bed rivers, the characteristics of pool-riffle sequence and the grain size distribution were determined [19,20]. Accordingly, the bedforms were constructed at a distance of 7 m from the flume entrance in order to prevent the effect of the end gate on the upstream flow. The pool-riffle sequence had a length of 5 m and the bed elevation changes were asymmetric in the flume width. The entrance and exit slopes of the pool section were the same indicating an angle of 7.3 degrees and the deepest depth of the pool was 10 cm under the bed form crest. After leveling the bed, a layer of gravel was added randomly across the flume to prevent any change in the bed topography. Changes in 3D bedform elevations and the longitudinal profile of pool section are shown in Figs. 3 and 4, respectively.

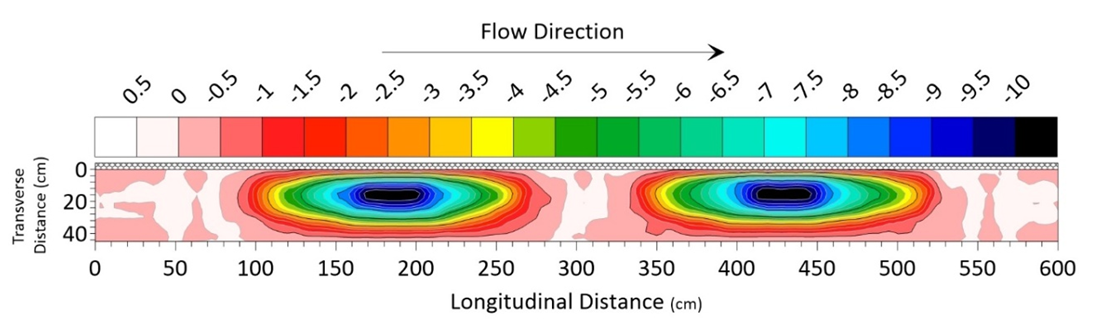Figure 3. Changes in three-dimensional bedform elevations in laboratory

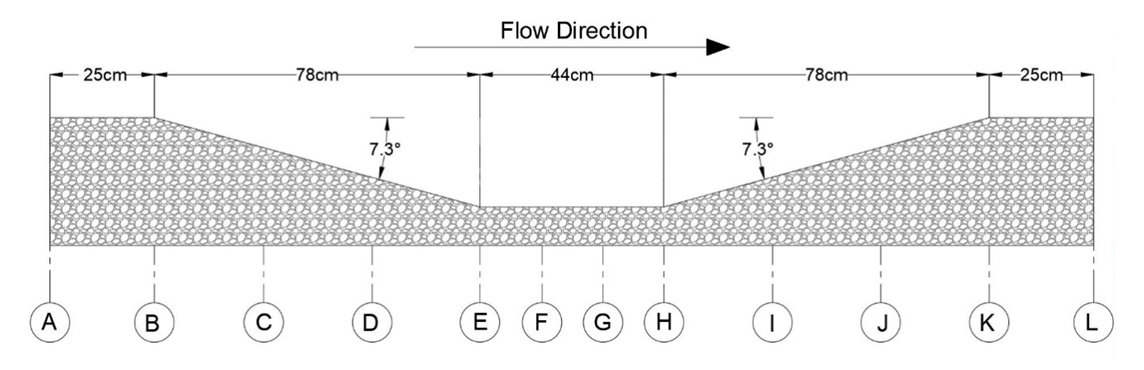Figure 4. Longitudinal profile of pool section

A row of reeds with 10 m length was used as natural vegetation only on one side of the flume wall. The average diameter of the stems was 12.8 mm and on average 80 stems were placed per meter of length of the flume wall. Note that the vegetation on wall was put on the left side, by moving in the direction of flow. The flume inside is illustrated in Fig. 5.

Figure 5. Interior view of laboratory flume

In the present study, the flow velocity was measured by using a micro-current meter instrument with high density. For this aim, a network was set for data organization, which is indicated in Fig. 6 and velocity measurements were done at the given points. In this network, the upper wall with vegetation, shown with green color, is the basis for calculating the horizontal distances (base axis) and the horizontal distance of axes 1, 2, 3, and 4 from the vegetation wall were 5, 15, 30, and 40 cm, respectively.

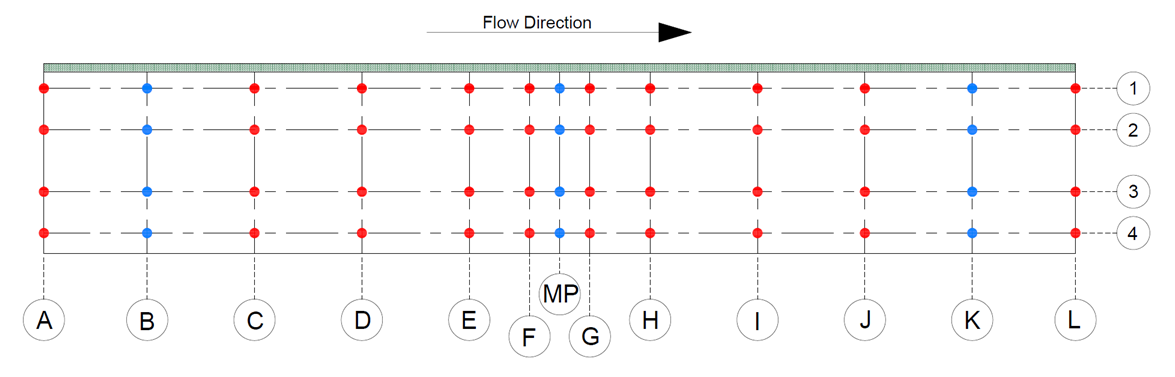Figure 6. A network setup in plan of flume

To construct the bed forms, two different types of gravel particles with diameters of 11.7 mm and 7.81 mm were used. The grain size distribution is presented in Fig. 7. The parameter of geometric standard deviation for these distributions was achieved as 1.2 and 1.3, respectively, which indicated the uniformity of the particle size distribution of the bed material.

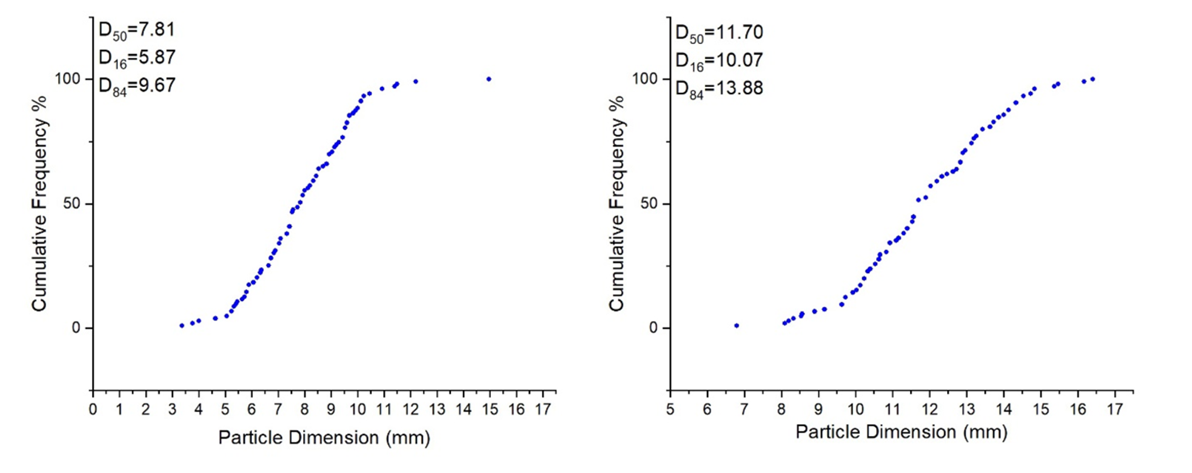Figure 7. Grain size distribution for bed materials

The flow discharges and other parameters related to the flow characteristics are presented in Table 1.

Table 1. Flow parameters in the experiments

The experiments were classified into four separate categories. In total more than 10,000 data were recorded. The characteristics of experiments are presented in Table 2.

Table 2. Characteristics and symbols of different categories of experiments

3. Results and Discussion

3.1. The Logarithmic Law Validation

Using 104 velocity profiles measured in near the bed zone and the inner layer, the validation of the logarithmic law was investigated for the interaction of 3D and wall vegetation. Kironoto and Graf (1995), Graf and Altinakar (1998), and Afzalimehr and Anctil (2000) considered the relative depth (y/h) up to 0.2 as the inner layer for 2D and without bed form in laboratory flumes [21-23]. However, Maddahi et al. (2016) reported the relative depth of 0.4, 0.8, and 0.33 for the validity of logarithmic law in gravel-bed rivers in the absence of bed forms. In the current research, the curve of depth of the logarithmic law for the first and fourth categories are demonstrated in Figs. 8 and 9, respectively [10]. For visual understanding, the relative depths of the validity of logarithmic law were classified into five separate categories, as shown in Fig. 10.

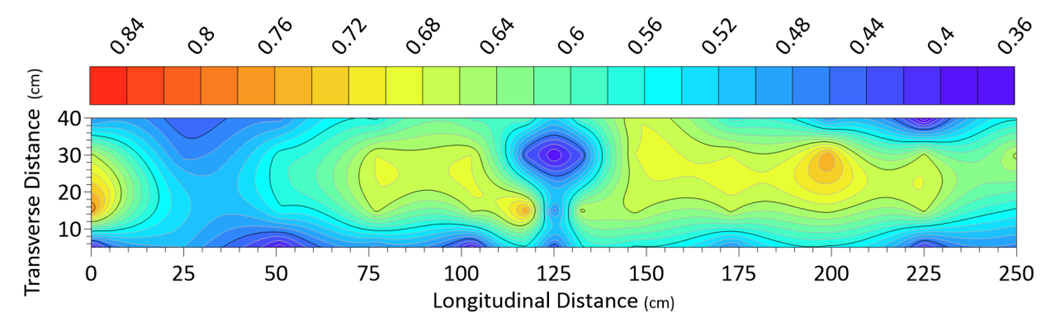Figure 8. The curve of elevation of logarithmic law validity in S1-V class

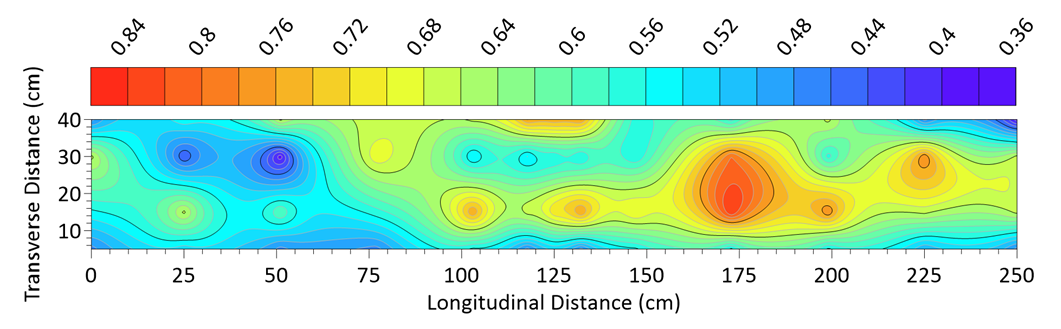Figure 9. The curve of elevation of logarithmic law validity in S4-NV class

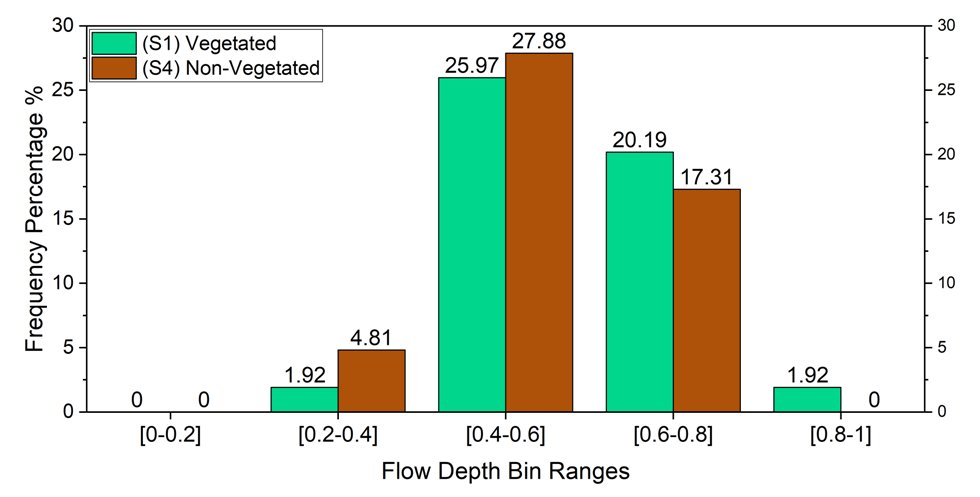Figure 10. Frequency percentage of relative depths of logarithmic law validity in the first and fourth classes of experiments

Figs. 8 and 9 show that the logarithmic law was valid in the presence and absence of vegetation for 3D bed forms, and the lower and upper relative depths of the logarithmic law validity were 0.36 and 0.84, respectively. Considering the frequency of categories in Fig. 10, it can be stated that the relative depth of validity was located in 53.8% of the profiles in the range of 0.4 to 0.6 and in 37.5% of the profiles in the range of 0.6 to 0.8.

This means that in more than 91% of the 104 profiles measured in this study, the depth of validity of the logarithmic law located in the range of 0.4 to 0.8, which was more than the relative depth of 0.2 reported for the case without wall vegetation and bed forms. The value of correlation coefficient for all measured profiles was more than 0.9, indicating a reasonable fit of the velocity data to the inner layer data in the presence of 3D bed form and wall vegetation.. Due to the large amount of data in this study, the correlation coefficients for logarithmic law and distance from vegetation were investigated, but no clear relationship was found between these two parameters.

3.2. Transverse Velocity Curves

For each category of experiments, 12 transverse velocity curves were presented. Since sections B, MP and K represent the pool, flat and riffle sections, respectively, the assessment and comparison of curves were done for all 4 categories of experiments in these three sections. The transverse velocity curves are shown in Figure 11, in which vegetation was located on the left vertical axis.

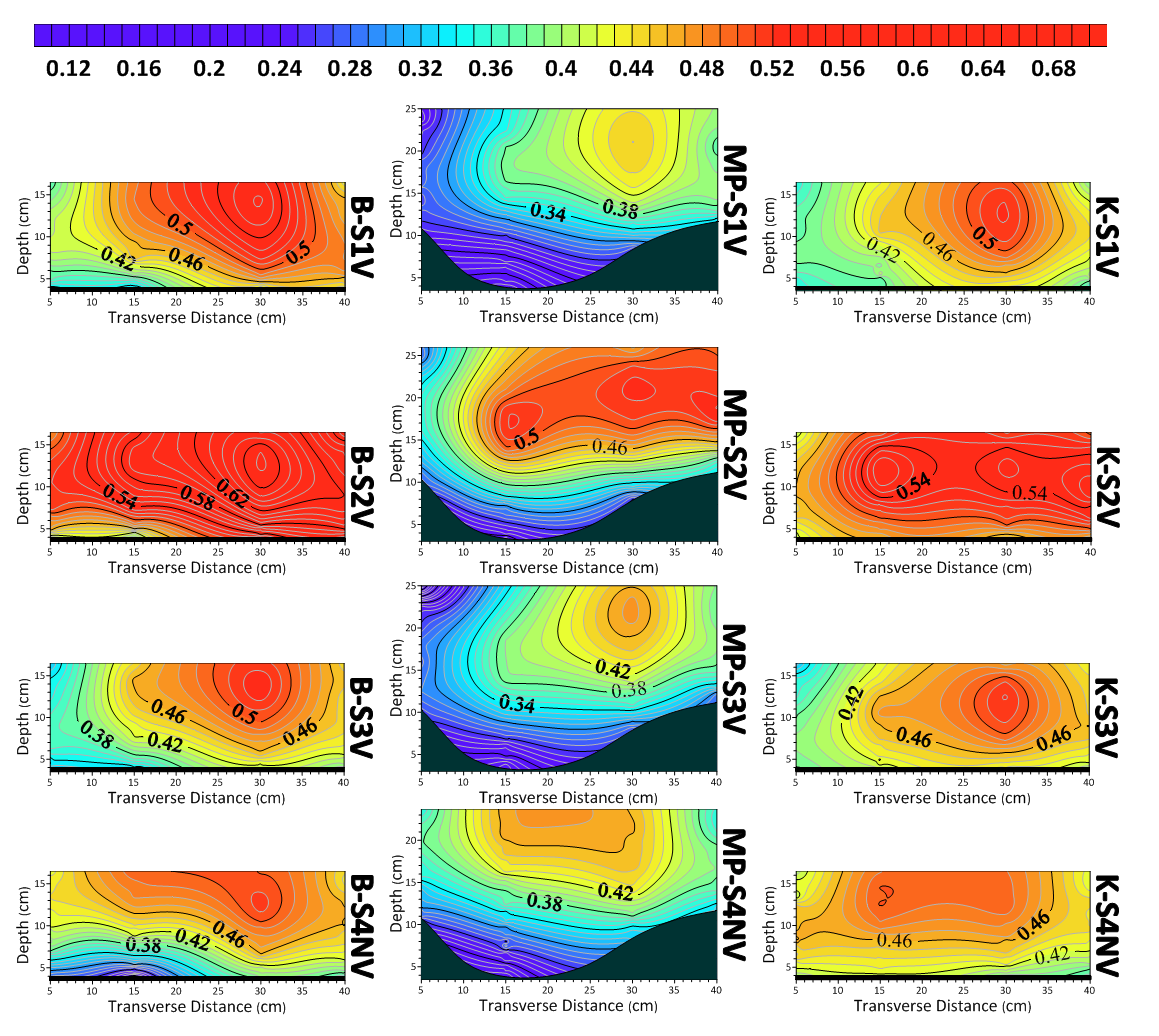Figure 11. Transverse velocity curves in sections of B, MP, and K

In the presence of vegetation in the riffle section due to the contraction of bed topography, large velocities occurred near the bed, while they occurred near the water surface at the bed in the pool section. This is consistent with the observations of Whiting and Dietrich (1991) and Kironoto and Graf (1995) for without vegetation and no bed form cases [21,24]. As can be seen, the highest velocity gradient occurred in the middle of the bed in all experiments. Due to the asymmetric three-dimensional bedforms, a transverse pressure gradient occurred in the channel, which inclined the maximum velocity zone towards the riffle section. Camaano et al. (2009) reported that at flows under dominant discharge, the transverse pressure gradient pushed the maximum velocity toward the inner bank of the river (shallower part) and in the flood phase, due to the dominance of the longitudinal momentum over the transverse pressure gradient, the maximum velocity was inclined towards the deeper part (pool section) [13]. This event was clearly observed in the present study owing to the fact that with the increase of flow, the maximum velocity zone expanded and inclined towards the pool section, and sometimes two separate maximum velocity zones formed. In addition, with increasing flow discharge, the velocity gradient increased in the middle zone and happened closer to the bed. Nezu and Rodi (1986) stated that due to the effect of walls in narrow channels, a strong transverse velocity component moved from the wall to the center of the channel near the water surface, creating a vertical velocity component from the water surface to the bed [25]. Between the vertical velocity and the lateral velocity, eddy currents perpendicular to the flow direction were created that drove the maximum velocity below the water surface. According to the results of a study conducted by Afzalimehr et al. (2010), even in a wide channel and presence of wall vegetation, the secondary flows were active due to the effect of vegetation and their intensity decreased by moving away from vegetation [14]. In experiments with the presence of vegetation, the maximum velocity zone formed below the water surface, and therefore the phenomenon of velocity dip was clearly seen, showing an active role of vegetation on wall in the secondary current generation. After removing the vegetation, the maximum velocity phenomenon approached the flow surface, which was due to weakened secondary currents. Also, the horizontal deviation of the maximum velocity zone towards the riffle section reduced, but the distribution of maximum velocity zone across the channel was still not symmetrical. Under the present conditions, vegetation played a more significant role in the deviation of the maximum velocity zone compared to 3D bed form role.

3.3. Role of 3D Bed form and Wall Vegetation on the Velocity Distribution

In this part, the dimensionless velocity profiles of B, MP and K sections in the first and fourth category experiments are presented, so that the effect of vegetation on velocity distribution can be investigated (Fig. 12 to 14). The blue dots are related to the presence of vegetation and the red dots are representative of the absence of vegetation.

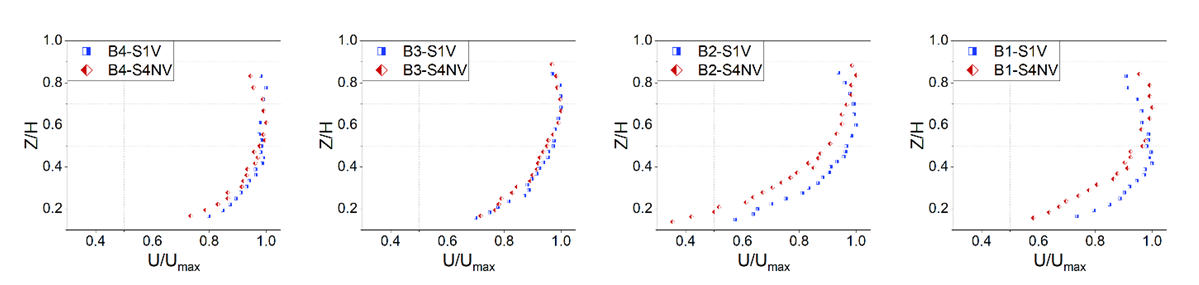Figure 12. Dimensionless velocity distribution of B section in S1V and S4NV experiments

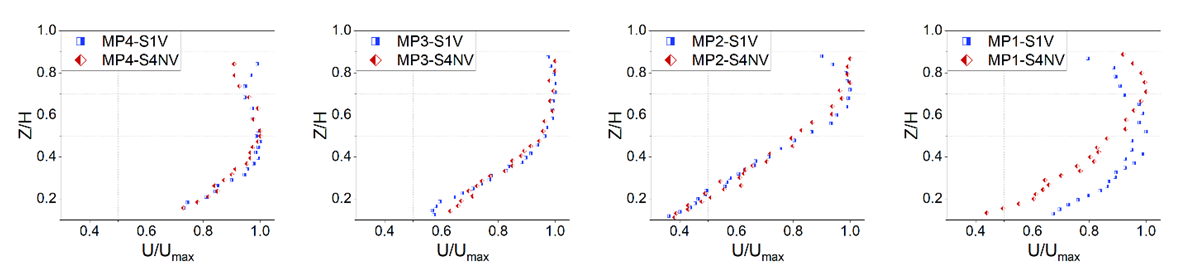Figure 13. Dimensionless velocity distribution of MP section in S1V and S4NV experiments

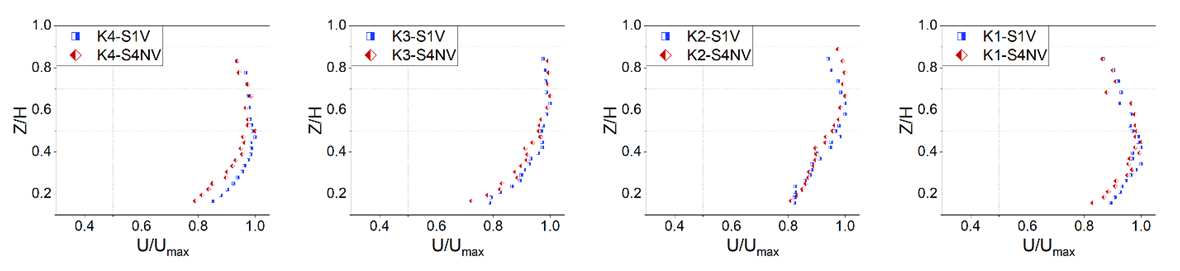Figure 14. Dimensionless velocity distribution of K section in S1V and S4NV experiments

In Fig. 12, adjacent to vegetation (point B1), the maximum velocity occurred at a relative depth of 0.48, while with the removal of vegetation, this value increased to 0.73. At a distance of 15 cm from the vegetation (point B2), the relative depth of occurrence of the maximum velocity was 0.6 and it had increased to 0.88 with the removal of the vegetation. This was due to the elimination of secondary currents generated by vegetation, which resulted in the attenuation of the velocity dip.

By moving away from the wall vegetation, the differences between velocity distributions declined, therefore, the effect of vegetation on the flow decreased. This observation is consistent with the results of Afzalimehr (2009) [26]. The smoother slope in point B2 profiles indicated that the velocity gradient in axis 2 was larger than in other axes. As indicated in the study of transverse velocity curves, the maximum velocity occurred below the water surface at all distances in the presence of vegetation.

Referring to Fig. 13, in the mid-section and adjacent to vegetation, there was a great deal of turbulence in the distribution of point velocities. At a distance of 15 cm from vegetation, there was no significant difference between the relative depths where the maximum velocity occur compared to the condition without vegetation. The velocity gradient was also similar in two cases. Also, because the two points of MP2 and B2 were both located on axis 2, the near-bed velocities of flat section indicated less discrepancies in two cases, compared to the pool section.

The range of velocity changes in the K section significantly decreased, compared to the mid-section (Fig. 14). This means that there was a large velocity gradient in the pool section rather than in the flat and riffle regions, which is in agreement with the observations of MacVicar and Roy (2007) [2]. At this section, the maximum velocity formed closer to the bed in both cases of with and without vegetation, compared to the pool section (Kironoto and Graf 1995) [21]. By moving away from vegetation to the axis 3 (at a distance of 30 cm from the vegetation), the agreement of profiles increased and in the axis 4 (at a distance of 40 cm from the vegetation) it has decreased again, which can be attributed to the effect of bare wall on the flow, because axis 4 was located 5 cm from the right wall.

The largest and lowest differences between the relative depths of maximum velocity were related to the pool and riffle sections, respectively. In all three selected sections, most changes in velocity profiles were related to the nearest axis to the vegetation (axis 1).

3.4. Shear Velocity Estimation

Shear velocity plays a significant role in river engineering parameters, therefore, an accurate calculation and selection of appropriate method for estimating shear velocity is of particular importance. In the present study, three methods of logarithmic law, parabolic law, and boundary layer characteristics method were used to estimate the shear velocity. For 24 selected points located on the B, MP and K sections, Fig. 15 presents a comparison of shear velocity estimation by the selected methods in this study.

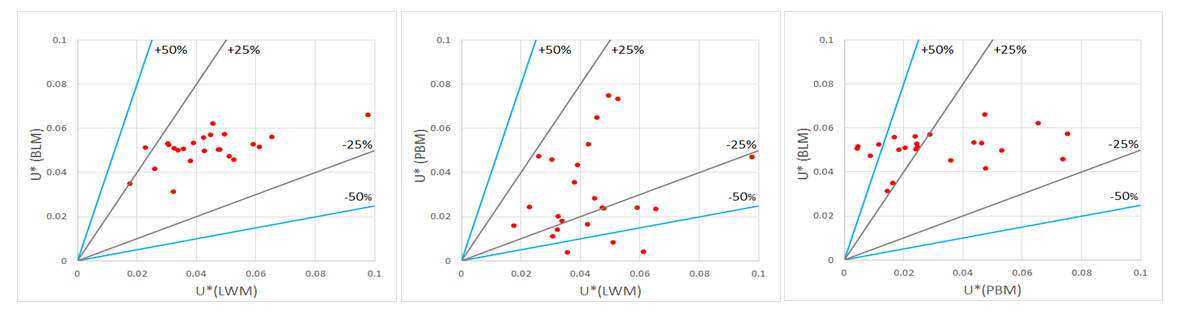Figure 15. Comparison of estimated shear velocity values, based on logarithmic law (LWM), parabolic law (PBM), and boundary layer characteristics (BLM) methods

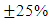The points located on the bisector line means a perfect agreement by two methods. Examination of the scatter of points indicates that the least difference in predicting shear velocity values was related to the boundary layer method and the logarithmic law in which data density was high around the bisector and more than 95% of the data were in the relative error range. This value decreased to 53% for the values obtained when comparing the parabolic law and the logarithmic law. Afzalimehr and Rennie (2009) used the boundary layer characteristics method to calculate the shear velocity in several rivers in Iran and Canada and found the log law to be valid in gravel-bed rivers [27]. Also, Fazlollahi et al. (2015) found over 2D riffle with wall vegetation and Shahmohammadi et al. (2018) for flow over vegetation patch reported the validation of the logarithmic law in shear velocity estimation in laboratory studies [4,28]. In the present study, the shear velocity values for all points in the network were calculated based on the boundary layer characteristics method, which not only used all data points in each velocity profile but also considered the velocity distribution over 3D bedforms. This method had a good agreement with the logarithmic law (Fig. 16), however, when the velocity distribution indicated some change in form, it was better to use the boundary layer characteristics method to estimate shear velocity.

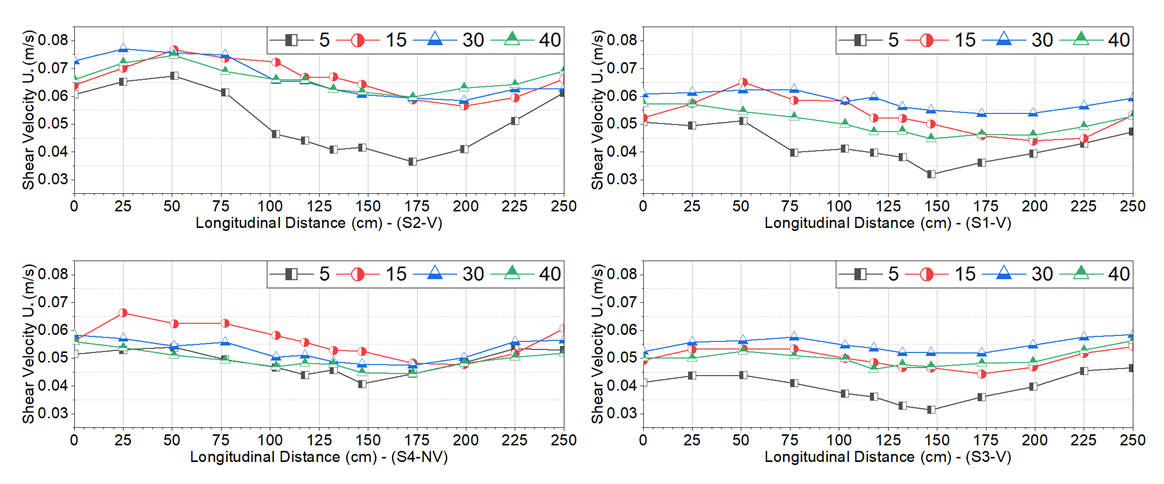Figure 16. Shear velocity values for different distances from wall for different experiments runs

Fig. 16 shows the trend of changes in the shear velocity values obtained by the boundary layer characteristics method at all distances from the wall for all experimental runs. Changes in the shear velocity values along the channel had the same-phase and sinusoidal variation. With a relatively good approximation, it can be claimed that the maximum shear velocity values were at the beginning of the pool section and mostly, the shear velocity in the axes adjacent to the center of the channel was higher than the values adjacent to the walls. In the study of Fazel Najafabadi et al. (2017), the shear velocities calculated using the logarithmic law method for two-dimensional pool-riffle sequence and the Reynolds shear stress method for three-dimensional sequence showed a parallel phase between changes in shear velocity and bed elevation [20]. However, in the present study for 3D bed forms a fuzzy difference was observed between shear velocities and bed elevation. With increasing discharge, the difference between the shear velocity values in the vicinity of vegetation and other axes as well as the range of changes in the shear velocity values increased. By reducing the median diameter of bed particles in the third run of experiments, the shear velocity values revealed less fluctuations, resulting in a more balanced distribution. In the presence of wall vegetation, the amount of shear velocity along the 3D bedform adjacent to the wall was less than along other longitudinal axes. This trend changed by removing vegetation from the wall in the fourth run showing the significant effect of vegetation on the shear velocity estimation. By removing the vegetation, the maximum values of shear velocity occurred along axis 2 (at a distance of 15 cm from the base wall), which corresponded to the pool section.

3.5. Shear Stress Variation

Many studies use shear stress rather than shear velocity to evaluate the key parameters of river engineering, including the Shields parameter which is a dimensionless shear stress. To investigate the shear stress, the values can be plotted on a simple diagram considering the location of each profile. In the present study, considering that the total number of profiles collected in all experiments was over 200, the same-stress curves in the bed were plotted so that the changes in this parameter can be easily observed. The direct estimation of shear stress is a difficult task, encouraging the researchers to calculate it indirectly by using the determination of shear velocity. In this section, using the shear velocity obtained by the boundary layer characteristics method for each velocity profile, the bed shear stress was calculated by 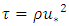, and for each experiment run, the bed stress curves are presented separately in Fig. 17. Note that in all plans the left wall is the bare wall.

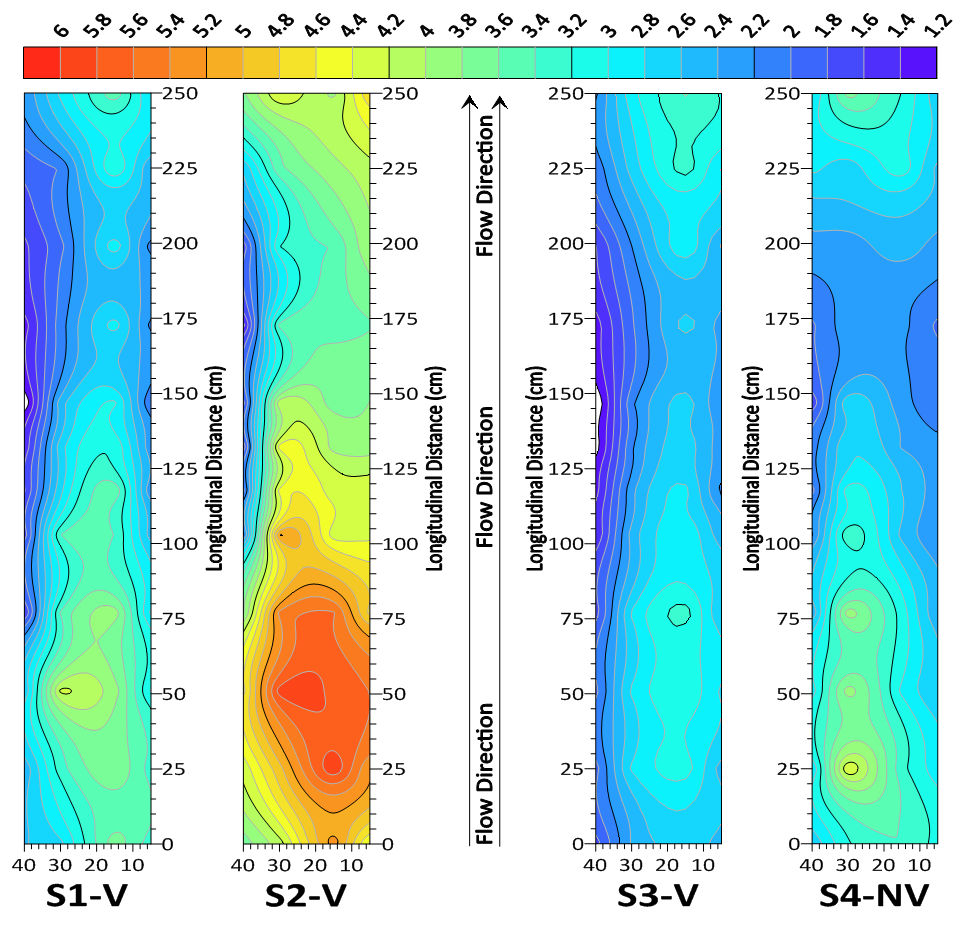Figure 17. Bed shear stress curves for all experiment runs

Results of simulations performed by Tokyay and Sinha (2020) in the pool-riffle sequences for four channel widths of 20, 30, 60 and 90 cm showed that the maximum and minimum bed shear stresses occurred in riffle and pool sections, respectively. In all experiments and in the connection slope of these two pool and riffle sections, the shear stress decreased by moving towards the pool section [8]. Macvicar and Rennie (2012) found that the highest shear velocity value estimated using near-bed velocities was related to the riffle section, while the lowest value occurred in the pool section indicating a range between 0.005 to 0.05 m/s [29].

In the current research, in the first to third runs with vegetation, the minimum stresses occurred in the vicinity of wall vegetation. By moving in the direction of flow, the occurrence of the lowest shear stress for all experiments was in the riffle region located on the exit slope of the pool section, and on reaching the riffle region, the stresses increased again. With increasing flow discharge, no noticeable changes happened in the location of the minimum and maximum shear stresses, however, the stress values increased significantly compared to the lower flow. By reducing the median diameter of the bed particles, the shear stress changes decreased. This means that the finer grains led to less changes in the shear stress values than did the coarse ones. On the other hand, the area of maximum shear stresses was inclined to the pool cross section in the absence of vegetation and the location of the minimum shear stresses was inclined to the center of the channel.

4. Conclusions

Environmental challenges for better restoration of water resources and river training demands a better understanding of the flow characteristics in the presence of vegetation and 3D bed forms. The present research focused on the presentation and estimation of flow velocity, shear velocity, and shear stress distribution through a 3D pool-riffle sequence, by considering the vegetation effect on one wall by using an experimental study. The following results can be drawn herein:

Fitting the velocity data to the near bed data (the inner layer) showed that in the presence of asymmetric three-dimensional pool-riffle bed form with and without wall vegetation, the logarithmic law is valid in more than 90% of velocity profiles, for more than 40% of the flow depth near the bed which is different from decelerating and accelerating flows in gravel-bed channels reported in the literature (e.g., Graf and Altinakar 1998). In fact, the wall vegetation influences the location of low depth where the logarithmic law is valid.

The location of maximum velocity (u_max) is a function of flow discharge, so that with increasing discharge, u_max tends to incline towards the pool section. The transverse pressure gradient due to the transverse asymmetry of the bedforms reduces the velocity values in the near bed region. The greatest velocity gradient was observed along the channel in the middle of the bedforms and the lowest value was observed at the end of the riffle region toward the crest. The velocity value near the water surface region (the outer layer) in the pool section was greater than in the riffle section. High velocity values also occurred near the water surface and near the bed in pool and riffle sections of 3D bedforms, respectively.

Investigation of velocity profiles indicated that maximum velocity occurred close to vegetation near the bed. By moving away from the vegetation wall, the difference between the maximum velocity and the surface velocity decreased to the vicinity of the bare wall and increased again at the closest axis to the bare wall.

The use of the boundary layer characteristics method to estimate shear velocity not only shows a good agreement with the estimated values by logarithmic law, but also it takes into account the velocity profile variations over 3D bedforms in the presence of wall vegetation.

The minimum shear stress occurred in the riffle section located on the exit slope of the pool section, and the maximum shear stress located at the entry slope of the 3D pool section and started decreasing toward the following riffle crest. In the presence of vegetation, the lowest shear stress occurred in the vicinity of vegetation. Increasing the flow discharge caused increased shear stress values, but did not cause a significant change in the location of the minimum and maximum stresses. Reducing the median diameter of the bed particles led to less change in the shear stress values.

There are some limitations in this study, including the artificial pool and riffle which may make different the results from the existing bed forms in coarse-bed Rivers. The sediment size variations may be significant in some sections in rivers which may not be easily found in in a laboratory scale. The current-meter cannot be used very near the bed to determine the velocity distribution and turbulence fluctuations, demanding more advanced tools to measure the flow velocity and turbulence in this region for future studies.