-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2021; 11(1): 1-9
doi:10.5923/j.jce.20211101.01
Received: Mar. 7, 2021; Accepted: Mar. 24, 2021; Published: Apr. 15, 2021

Centrifuge Investigation of Tunnel Face Displacement in Two-layer Soils
Tuan Anh Nguyen1, Minh Anh Trong Nguyen2
1Transportation Engineering Faculty, Ho Chi Minh City University of Transport, Binh Thanh Dist., Ho Chi Minh City, Viet Nam
2Airports Corporation of Vietnam, Tan Binh District, Ho Chi Minh City, Viet Nam
Correspondence to: Tuan Anh Nguyen, Transportation Engineering Faculty, Ho Chi Minh City University of Transport, Binh Thanh Dist., Ho Chi Minh City, Viet Nam.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the author performed two centrifuge model tests at the University of Science and Technology of Hong Kong for two cases where the tunnel was located at cover over diameter (C/D) of 1.5 and 3.3 to investigate the passive failure and deformation mechanism due to tunneling in two-layer soils, sand and clay. The tests were carried out on a 1/100 scale miniature model. The experimental process simulated the progress of the tunnel face with a speed of 0.2mm/s (equivalent to 15m per day in practice), and displaced to 40mm then stopped. Linear variable differential transformers (LVDTs) are used to measure the ground transitions during the testing process. The particle image velocimetry (PIV) technology measures the movement of soil in front of the tunnel face. The loadcells attached to one end of the tunnel face in order to obtain the passive pressure exerted on the tunnel face. As the tunnel face displacement, the ground in front of the tunnel face is shifted forward, while the ground which is far from the surface of the tunnel is pushed outward, effected on the ground and thus causes the ground to emerge so form a breakout. The partial failure mechanism in front of the tunnel face is similar to localised cutting mechanism. When the observation failure mechanisms are idealized by continuous lines, the failure mechanism of ground in front of the tunnel face is shaped like a funnel.
Keywords: Two-layer soils, Centrifuge test, Displacement, Mechanism, Tunnel face
Cite this paper: Tuan Anh Nguyen, Minh Anh Trong Nguyen, Centrifuge Investigation of Tunnel Face Displacement in Two-layer Soils, Journal of Civil Engineering Research, Vol. 11 No. 1, 2021, pp. 1-9. doi: 10.5923/j.jce.20211101.01.
Article Outline
1. Introduction
- Tunneling construction has become an indispensable trend for traffic systems by exploring underground space in modern cities. It is the case, however, that each project has different conditions of geology, hydrography, tunnel structure, etc [1]. So profound research is constantly needed to assess the influences of tunneling on adjacent buildings.Broms & Bennermark, Davis et al., Kovári & Anagnostou, Mair et al., Mollon et al., etc. have conducted such studies to investigate and evaluate the stability of tunnel faces, as well as determining ground displacement in front of the tunnel faces [2-6]. These studies, however, are only applicable to particular cases within the scale of research, mainly for failure of active earth pressure.Attwell, Mair et al., O’Relly & New, Sang-Hwan Kim et al., A. Sirivachiraporn & N. Phienwej, J. N. Shirlaw, Schmidt, Wei-I. Chou & Antonio Bobet, etc. used experimental methods based on measured field data to evaluate the stability of soil in front of tunnel faces [7-15]. These methods only consider a 2D plane condition and do not take 3D effects into account during the tunnelling process. Additionally, field experiments are somewhat limited by expensive monitoring instruments and some other safety issues related to failures at tunnel entrances. It will be very costly and not viably repeatedly executed for large-scale models.Atkinson and Potts, Chambon and Corte, Gregor Idinger et al., Kamata and Mashimo, and P. Oblozinsky and J. Kuwano performed centrifugal tests to study active failure mechanisms and pressures at the inhomogeneous layer (sand or clay) of the tunnel face, or only investigated passive pressure at the tunnel face, but have not provided an equation to determine this passive pressure [16-21].Numerical analyses have been allowed in studies of 3D failure mechanisms of the ground in front of the tunnel face as influenced by a construction sequence. Yet, Finite Element Method (FEM) models are always controlled by boundary conditions, so these would not be able to precisely model the tunneling process in the soil environment [22-25]. Therefore, a systematic investigation of the passive failure mechanisms of the soil in front of the tunnel face is needed. Similarly, the influences of tunnel construction sequences must also be considered to determine the passive failure pressure while the tunnel is progressing forwards.This paper presents details of a centrifuge model setup and test procedures and the induced ground surface displacement resulting from the tunnel face displacement obtained from the centrifuge tests.
2. Materials and Methods
2.1. Centrifuge Modeling
2.1.1. Kinematics of Centrifuge Modeling
- Figure 1 shows the plan view of a soil model in a spinning centrifuge. Consider a soil element located at an arbitrary point A. At a given time, the location of the arbitrary soil element A in the model container can be expressed as a vector summation [26]:
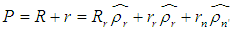 | (1) |
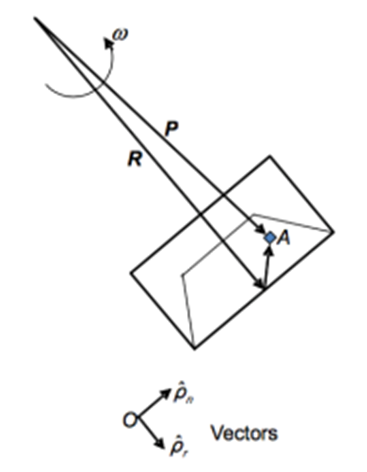 | Figure 1. Plan view of a soil model in a spinning centrifuge [27] |
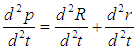 | (2) |
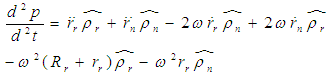 | (3) |
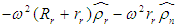 denotes centripetal acceleration (due to the spinning of the centrifuge);
denotes centripetal acceleration (due to the spinning of the centrifuge); 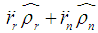 describes the acceleration of a particle, P, relative to the centrifuge platform; and
describes the acceleration of a particle, P, relative to the centrifuge platform; and 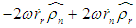 refers to Coriolis acceleration.
refers to Coriolis acceleration.2.1.2. Fundamental Principles of Centrifuge Modeling
- The fundamental principle of centrifuge modeling is to recreate stress conditions that would exist in a prototype by increasing n times the “gravitational” acceleration in a 1/n scaled model in the centrifuge [28]. Stress replication in the 1/n scaled model is approximately achieved by subjecting model components to an elevated “gravitational” acceleration, a:
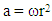 | (4) |
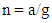 | (5) |
2.1.3. Scaling Laws in Centrifuge Modeling
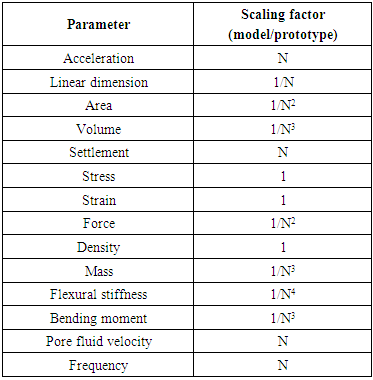
- For centrifuge model tests, scaling laws are generally derived through dimensional analysis, from the governing equations for a phenomenon or from the principles of mechanical similarity between a model and a prototype [29,30].Soil behavior depends on and is governed by effective stress created initially from the unit weight itself. A fundamental principle of centrifuge modeling is to simulate correctly the real stress level of a prototype in a scaled-down model [28].
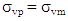 | (6) |
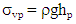 | (7) |
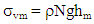 | (8) |
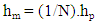 | (9) |
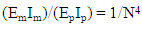 | (10) |
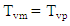 | (11) |
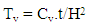 | (12) |
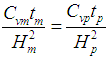 | (13) |
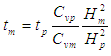 | (14) |
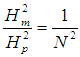 | (15) |
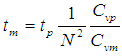 | (16) |
|
2.2. Experimental Program
- Two cases of tunnel excavation with different C/D ratios were done in two-layer soils, with an upper layer of medium sand and a lower soil of stiff clay. Tests T1 & T2 corresponding to C/D values of 1.5 and 3.3 were to investigate passive pressure at the tunnel face. Details on the centrifugal tests are presented in Figures 3 and 4.
 | Figure 2. Sand layer pouring [25] |
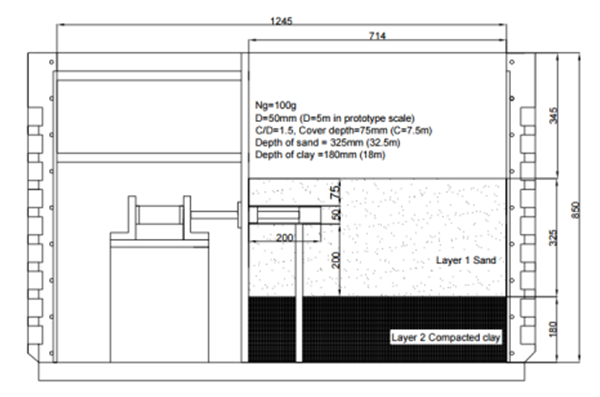 | Figure 3. Cetrifuge test T1 for tunnel at C/D = 1.5 [25] |
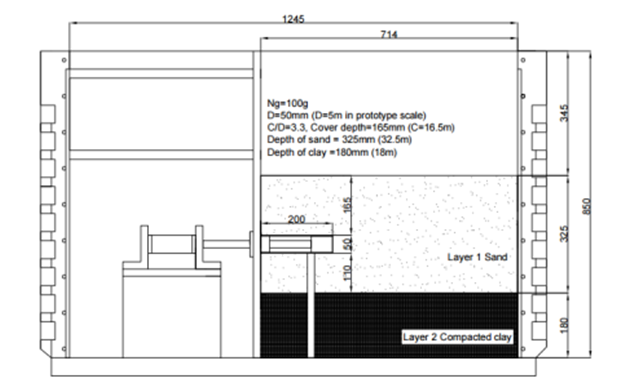 | Figure 4. Cetrifuge test T2 for tunnel at C/D = 3.3 [25] |
2.2.1. Soil Preparation
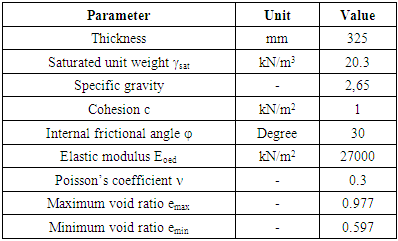
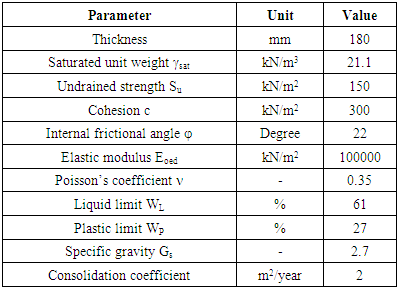
- The soil model consists of two layers, the 180 mm clay layer was overlaid by a 325 mm thick sand layer. Firstly, the compacted clay layer was laid and then sand was poured into the test container through a funnel with a drop height of 500 mm.In order to saturate the sand, an aluminum plate with an O-ring was placed above the hard box. A vacuum was maintained for two hours, and then carbon dioxide was pumped through the drainage system to replace the remaining air. The vacuum was subsequently maintained for three more hours while water from the tank was supplied through the drainage systems to the soil. When the water level reached the required level at the sand surface, the saturation process terminated. The entire saturation process took about 40 minutes [31]. The soil parameters of sand and clay are shown in Tables 2 and 3.
|
|
2.2.2. Installation of the Model Test
- The rectangular box model was applied to the centrifuge model. The inside profile of the model container was 1245 mm long, 850 mm high and 350 mm wide. An observation window was installed in the front of the container. The panels were fastened to the front with a glass plate, 12.7 mm thick and with dimensions of 850 mm x 715 mm, in contact with the sand. The glass was used for the purpose of easily controlling the choice of tool while reducing the friction between the tunnel face and the sand. A 25.4 mm thick aluminum plate was used to separate the soil from the loading system. The aluminum plate was joined by six aluminum struts attached to a side wall of the container.Figure 5 shows the original model tunnel used in the T1 and T2 tests. The tight tunnel end was 50 mm long, made of semicircular aluminum tube with a diameter of 44.6 mm. A cylindrical shell made from an empty aluminum tube, with an outer diameter of 50 mm, a length of 200 mm and a wall thickness of 2.7 mm, was separated along the central plane. An empty piston 20 mm in diameter and 150 mm in length was screwed to the beginning of the tunnel, and a 25 mm long end block was placed at the end of the loading piston. A cylinder surrounded a block at one end of the tunnel and was tightly tied to the other end block. The loading piston and tunnel face block also served as load cells with full Wheatstone bridge strain gauges bonded to its external surface and protected by epoxy coating [30]. The performance and reliability of the strain gauges decreased over time, due to the seepage. In order to reduce the friction between the block at the beginning of the tunnel and the sand and glass layers to transfer to the load cell and to ensure the performance and reliability of the underwater load cell, a new load piston and block at the beginning of the tunnel were established based on the improved design.
 | Figure 5. Rectangle box model [25] |
 | Figure 6. Loading system affecting the tunnel [25] |
2.2.3. Instrumentation
- A. Measurement of Surface Soil DisplacementSurface soil displacement due to tunneling was measured by LVDTs of the Macro Sensor’s PR 750 series. LVDTs have different amplitudes of ± 20 mm and ± 80 mm, with an output source of ± 10 V under the normal DC 10 V power supply used. Horizontal and vertical surface displacements were monitored by eight LVDTs, as shown in Fig. 7 (a, b, c).
 | Figure 7. LVDTs before (a) and after installation (b), (c) [33] |
 | Figure 8. Camera tracking ground displacements [33] |
 | Figure 9. Device measuring the tunnel face pressure [33] |
 | Figure 10. The model after the completion of installation [33] |
2.2.4. Experimental Procedure
- The experimental model was transferred to and installed on a spinning centrifuge table after the model preparation and final inspection were completed. The LVDTs were calibrated and installed, as in Figure 7.
 | Figure 11. Tunnel advancement in centrifuge test with C/D = 3.3 [33] |
3. Results and Discussion
- The surface displacement due to the tunnel construction can be described by the Gaussian curve proposed by Peck and Schmidt [33]. It is assumed that the settlement on the excavated surface can be approximately relative with respect to the curves calculated by equation (17),
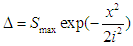 | (17) |
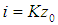 | (18) |
|
|
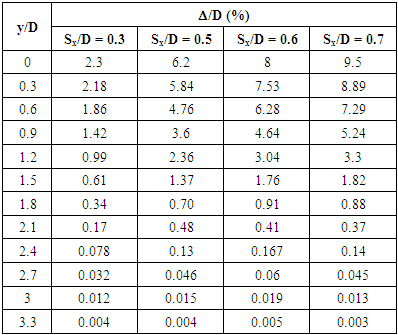
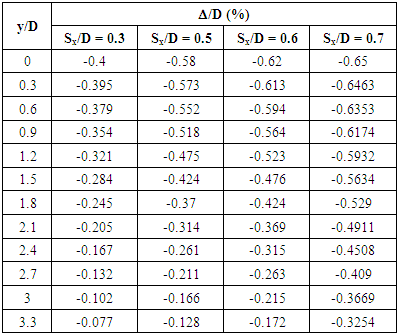
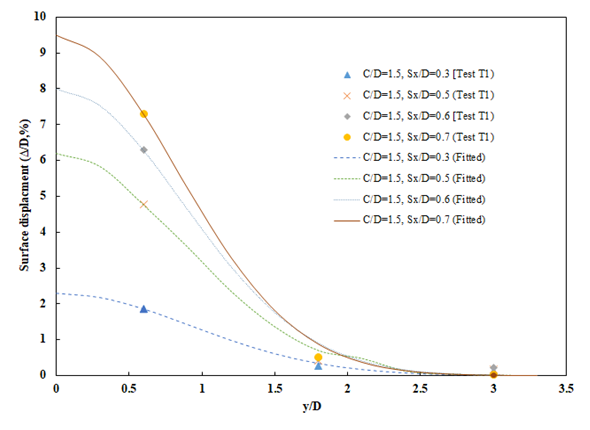 | Figure 12. The surface displacement in front of the tunnel face in test T1 [25] |
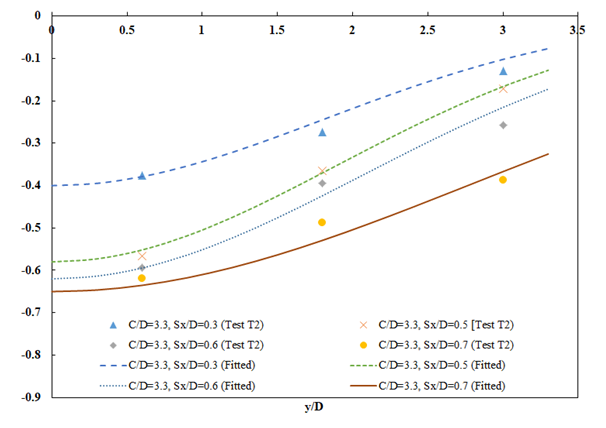 | Figure 13. The surface displacement in front of the tunnel face in test T2 [25] |
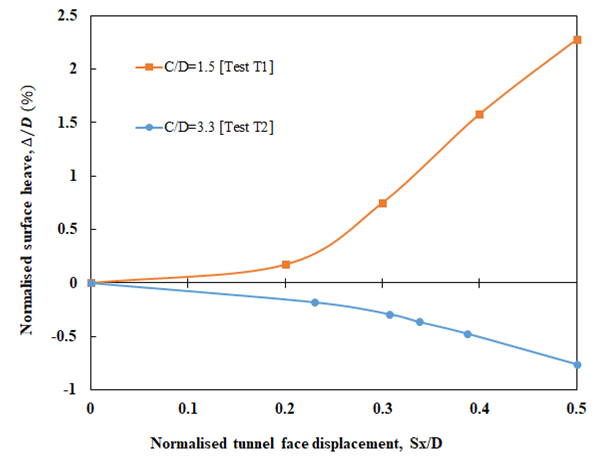 | Figure 14. The surface displacement in the vertical of tunnel in experiments T1 and T2 [25] |
4. Conclusions
- Deformation mechanism: with tunnels located at a shallower depth with a C/D ratio of 1.5, as the tunnel moved forward, the soil around the tunnel face bulged outward. The displacement value increased significantly with the increase in Sx/D ratio. For tunnels at a C/D ratio of 3.3, unlike with tunnels located at a shallower depth, the surface subsidence shows a more concave settlement curve as the thickness of the cover increases from 1.5D to 3.3D. In addition, the settlement curve has a wider deformation area than the settlement curve when the tunnel is located at 1.5D from the ground face.Most ground deformations occur within a distance of 3 times the diameter across the tunnel. Both observed longitudinal and transverse heaves are well described by Gaussian distributions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML