Imran S. M. , Raghunandan Kumar R. , Arun Kumar
CHRIST (Deemed to be University), Bangalore
Correspondence to: Raghunandan Kumar R. , CHRIST (Deemed to be University), Bangalore.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this research, optimum design of reinforced cement concrete (RCC) ribbed slab, also known as waffle slab according to the Indian RCC code (IS 456:2000) is presented. The objective function is the combined cost of the reinforcement, concrete and formwork which sums up the cost of the ribbed slab. The structure is analyzed using the direct design method. The objective function is developed after studying the ribbed slab in detail. The optimization process is carried out for different grades of concrete. The comparative results for different grades of concrete are enumerated and laid out in the tabulated form. Optimization for reinforced cement concrete (RCC) ribbed slab is illustrated and the results of the optimum design and conventional design are compared. Optimization problem is a constrained nonlinear programming problem (NLPP). The mathematical model is analyzed by using MATHEMATICA software. From the analysis, it was found that savings up to 25 percent can be obtained by optimizing the reinforced concrete ribbed slab.
Keywords:
Ribbed slab, Reinforced concrete, Structural optimization, Effective depth
Cite this paper: Imran S. M. , Raghunandan Kumar R. , Arun Kumar , Optimum Design of a Reinforced Concrete Ribbed Slab, Journal of Civil Engineering Research, Vol. 10 No. 1, 2020, pp. 10-19. doi: 10.5923/j.jce.20201001.02.
1. Introduction
A ribbed slab also called as waffle slab is a two-way joist or coffered slab, essentially consisting of a thin top slab acting compositely with a closely spaced orthogonal grid of beam ribs. In flat ribbed slabs, solid heads are formed around the columns to resist the high bending and shear stresses in these critical areas. In contrast to a joist which carries loads in a one-way action, a waffle or ribbed system carries the loads simultaneously in two directions. The system is more suitable for square bays than rectangular bays. [9]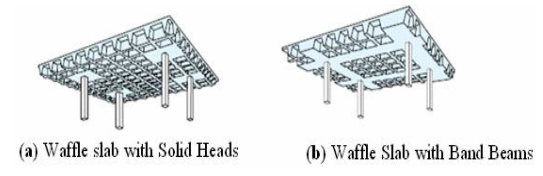 | Figure 1. Waffle (Ribbed) Slab Types [1] Source: IJCSE |
Optimum design of reinforced concrete elements plays a vital role in economical design of reinforced concrete structures. Thus, a designer has to perform a number of design-analyze cycles before converging on the best solution. In Ribbed Slab construction, as it involves, the slab, beams (ribs) running in both the directions beneath the slab (concrete, steel and formwork) in addition to safety, economic aspects also need to be considered as it is going to make a major impact on the overall cost of the structure. Hence, there is a need for an optimum design of ribbed slabs.Research, on optimization of ribbed slabs is exceptionally scarce as there is little to none work done on the subject. The material consumption and economical aspects of ribbed slabs are often neglected by the designers. It is important to think about the importance and efficacy of optimization of such structural elements.
2. Objectives
2.1. To analyze and design three ribbed slabs manually of 10m square module, 12.6 m square module and 21 m square module with 1.4 m grid spacing.2.2. To study the optimization of effective depth of the beams using MATHEMATICA and consequently the overall cost of the system.2.3. To compare the cost with respect to the standard design principles.
3. Review of Related Literature
Research on optimization of ribbed slabs is very limited, as there is hardly any work done on the subject. Among the papers reviewed, one of the most important ones is the work done by Kiran Patil et al [2013] [2] who have investigated the optimum design of reinforced concrete flat slab with drop panel. The objective function considered is the total cost of the structure including the cost of slab and column. The cost of each structural element included, the material and labor for reinforcement, concrete and formwork. Comparative study was carried out for various grades of concrete and steel. The optimum and conventional design results are compared. The cost of the slab was found increasing rapidly with increase in grades of concrete and steel. The percentage reduction in optimum cost of the slab was found to be directly proportional to the number of spans.Another important work was done by Alaa C Galeb, and Zainab F. Atiyah [2014] [1] who investigated the optimum design of reinforced concrete waffle slabs (two way ribbed) by using genetic algorithms. Two cases were studied, the first was waffle slabs with solid heads and the other, waffle slabs with band beams along column centrelines. Direct design method was used for the structural analysis and design of slabs. The objective function represented cost of concrete, formwork and reinforcement for the slab. The design variables were effective depth of slab, rid width, spacing between ribs and top slab thickness. Constraints included the dimensions of rib, top slab thickness and area of steel reinforcement, to satisfy flexural and minimum area requirements. Algorithm was developed using MATLAB to perform structural analysis and the optimization process was carried out using the built-in genetic algorithm toolbox.
4. Analytical Work
Formulations are done by following IS 456:2000 guidelines and results of ribbed slab for different depths and spans are calculated by using MATHEMATICA software.Case 1: Ribbed slab of size 10000mm x 10000 mm square panelCase 2: Ribbed slab of size 12600 mm x 12600 mm square panelCase 3: Ribbed slab 21000 mm x 21000 mm square panel  | Figure 2. Modelling of 1000 0mm x 10000 mm span |
The structural analysis of ribbed slab system is carried out using direct design method as per Bureau of Indian Standards, IS 456:2000. In this method, a ribbed slab having a square column layout is divided into a series of longitudinal and transverse planes. Each frame consists of ribs and strips of slabs. In each direction, equivalent frames are structurally analyzed to obtain the total bending moments and shear forces at different sections of the slab. It is assumed that the width of the beams is divided into two strips namely column and middle strips. Negative and positive bending moments are determined in column and middle strips. The punching shear is checked in the solid head portion and the shear stress at the ribs is calculated. Then, the depth is checked to resist the bending moment. The bending moments and areas of steel at each section are calculated according to the design bending moment obtained in each section of column and middle strips.This current analysis is constricted to rectangular form of slabs.
4.1. Objective Function (Cost Function)
The objective Function was developed after studying the ribbed slab in detail. It was formulated with respect to the design variable, effective depth.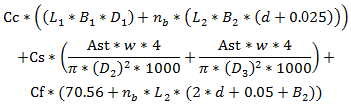 Where,Cc is the cost of the concreteCs is the cost of the steelCf is the cost of the formworkL1 is the length of the SlabL2 is the length of the beamB1 is the breadth of the slabB2 is the breadth of the beamD1 is the depth of the topping slabD2 and D3 are the diameters of the reinforcement barsNb is the number of ribsAst is the area of steel25mm is the cover for beamsw is the unit weight of the reinforcement bard is the effective depth of the beam
Where,Cc is the cost of the concreteCs is the cost of the steelCf is the cost of the formworkL1 is the length of the SlabL2 is the length of the beamB1 is the breadth of the slabB2 is the breadth of the beamD1 is the depth of the topping slabD2 and D3 are the diameters of the reinforcement barsNb is the number of ribsAst is the area of steel25mm is the cover for beamsw is the unit weight of the reinforcement bard is the effective depth of the beam
4.2. Design Variables and Constraints
4.2.1. Design Variables
This optimization problem of a ribbed slab includes the following design variable which is an independent design variabled = Effective depth of the beam.Effective Depth: Effective depth is the depth of a beam as measured from the top of the member to the centroid of its tensile reinforcement.The other independent variables are 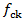 = characteristic compressive strength of concrete.Cost of the slab.
= characteristic compressive strength of concrete.Cost of the slab.
4.2.2. Constraint Equations
1. Shear Constraint: 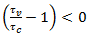
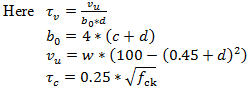 2. Minimum depth constraint:
2. Minimum depth constraint: 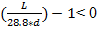 Where,
Where,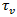 is the nominal shear stress
is the nominal shear stress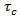 is the permissible shear stress
is the permissible shear stress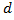 is the design variable, effective depth
is the design variable, effective depth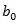 is the width of solid head of the slab
is the width of solid head of the slab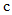 is the width of solid portion of the slab
is the width of solid portion of the slab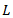 is the span of slab in both directions
is the span of slab in both directions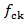 is the characteristic compressive strength of concrete.w is the factored load acting on the slab
is the characteristic compressive strength of concrete.w is the factored load acting on the slab
4.3. Design Optimization Procedure
The process of finding the conditions that give the maximum or minimum value of the function.The optimum cost design of ribbed slab is formulated in which the objective (cost) function and the constraint functions are nonlinear functions of the design variable. This nonlinear programming problem is solved by using fixed step size method. In fixed step size method, problem is checked for different values with constant step length. In this particular case, the step length considered is 25 mm. It is so considered, because the effective depth of the beam, which is the design variable in this problem is varied inch by 25 mm in practice. The effective depth is varied with the codal provisions and the optimization of the effective depth and the percentage of steel reinforcement is made to obtain the overall optimization of the ribbed slab. Different Conditions and Parameters for Analysis and Design:For comparative study consideration, the following parameters are considered for different results 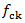 = Characteristic Compressive Strength of concrete = M25, M30fy = Characteristic Strength of steel = Fe 415Cost of Concrete: M25 = Rs.9000 per CumM30 = Rs.10000 per CumM35 = Rs.10500 per CumCost of Steel:Fe415 = Rs.60000 per Metric TonneCost of Formwork = Rs.400 per SqmSlab of sizes of 10000 mm x 10000 mm, 12600 mm x 12600 mm and 21000 mm x 21000 mm are considered in the research.
= Characteristic Compressive Strength of concrete = M25, M30fy = Characteristic Strength of steel = Fe 415Cost of Concrete: M25 = Rs.9000 per CumM30 = Rs.10000 per CumM35 = Rs.10500 per CumCost of Steel:Fe415 = Rs.60000 per Metric TonneCost of Formwork = Rs.400 per SqmSlab of sizes of 10000 mm x 10000 mm, 12600 mm x 12600 mm and 21000 mm x 21000 mm are considered in the research.
5. Results
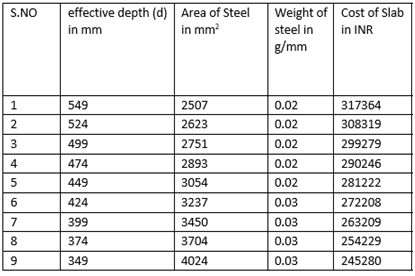
Case 1: i) Span of size 10000 mm x 10000 mmGrade of concrete=M25Cost of concrete = Rs.9000 per Cum.Cost of steel = Rs.60000 per MTCost of formwork= Rs.400 per SqmTable 1. Parameters of the Ribbed Slab for M25 Grade Concrete – 10000 mm x 10000 mm
 |
| |
|
From the above Table 1: for M25 grade of concrete, it is observed that area of steel is increasing by 60 percent with decrease in effective depth.Also from Figure 3(a), it is observed that, the weight of steel is increasing by 50 percent with decrease in effective depth.The cost of the slab is increasing by 29 percent with increase in effective depth as observed from Figure 3(b):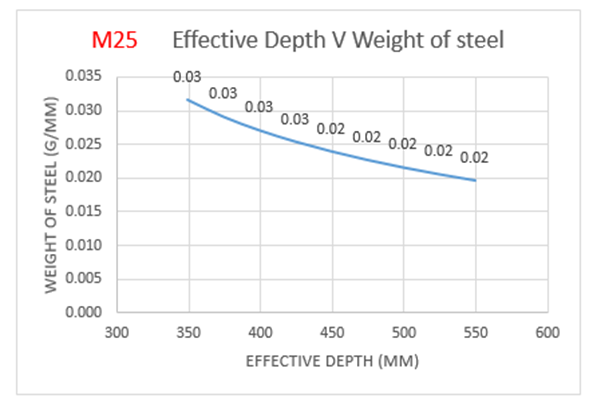 | Figure 3(a). Variation of effective depth to weight of steel for M25 Grade Concrete |
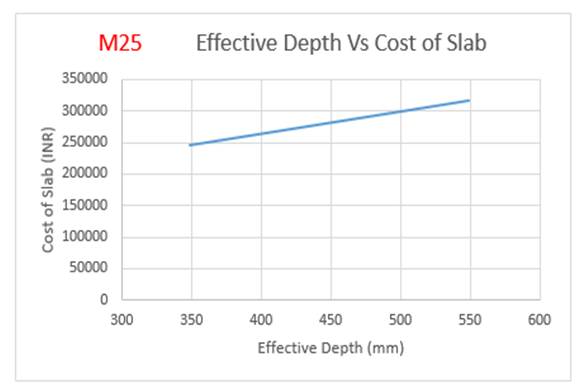 | Figure 3(b). Variation of effective depth to cost of slab for M25 Grade Concrete |
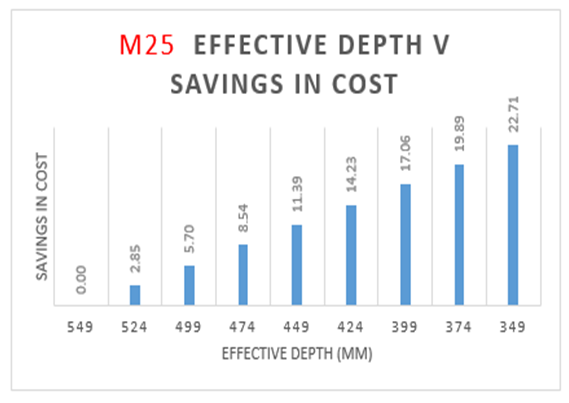 | Figure 3(c). Variation of effective depth to savings in cost for M25 Grade Concrete |
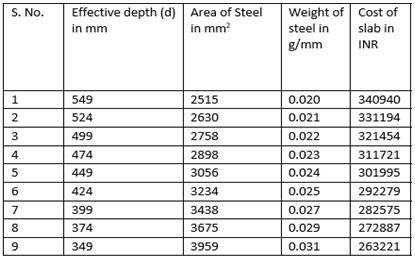
Case 1: ii) Span of size 10000 mm x10000 mmGrade of concrete=M30Cost of concrete = Rs.10000.00 per cumCost of steel = Rs.60000.00 per MTCost of formwork= Rs.400.00 per SqmTable 2. Parameters of the Ribbed Slab for M30 Grade Concrete- 10000 mm x 10000 mm
 |
| |
|
From the above Table 2: for M30 grade of concrete, it is observed that area of steel is increasing by 57 percent with decrease in effective depth.Also from Figure 4(a), the weight of steel is increasing by 50 percent with decrease in effective depth.The cost of the slab is increasing by 29.5 percent with increase in effective depth as observed from Figure 4(b):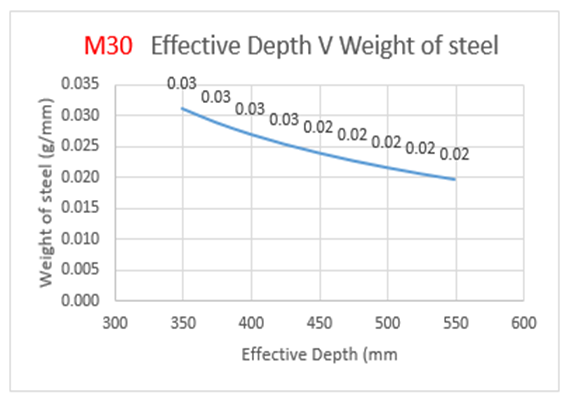 | Figure 4(a). Variation of effective depth to weight of steel for M30 Grade concrete |
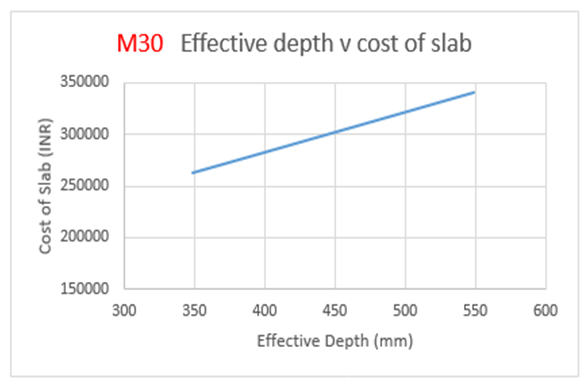 | Figure 4(b). Variation of effective depth to cost of slab for M30 Grade Concrete |
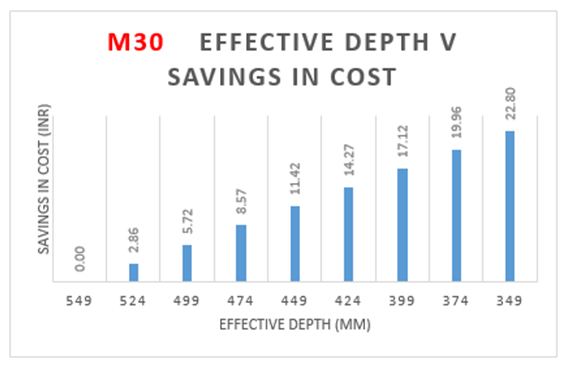 | Figure 4(c). Variation of effective depth to savings in cost for M30 Grade Concrete |
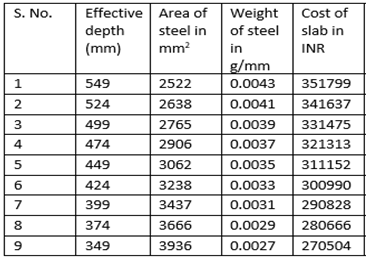
Case 1 iii) Span of size 10000 mm x 10000 mmGrade of concrete=M35Cost of concrete = Rs.10500.00 per CumCost of steel = Rs.60000.00 per MTCost of formwork= Rs.400.00 per SqmTable 3. Parameters of the Ribbed Slab for M35 Grade Concrete -10000 mm x 10000 mm
 |
| |
|
From the above Table 3:, for M35 grade of concrete, it is observed that area of steel is increasing by 56 percent with decrease in effective depth.Also from Figure 5(a):, the weight of steel is increasing by 56 percent with decrease in effective depth.The cost of the slab is increasing by 30 percent with increase in effective depth as observed from Figure 5(b):The optimum point here is observed to be 349 mm (effective depth) as it results in savings of 23.11 % over normal design.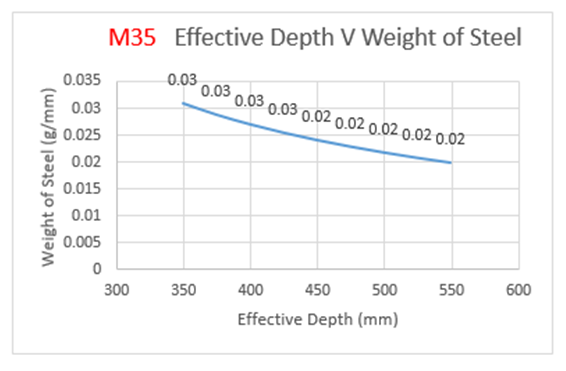 | Figure 5(a). Variation of effective depth to weight of steel for M35 Grade Concrete |
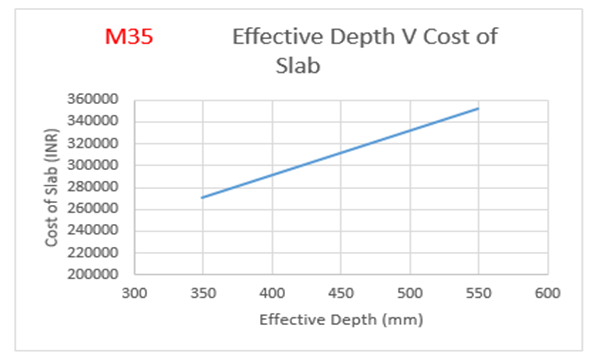 | Figure 5(b). Variation of effective depth to cost of slab for M35 Grade Concrete |
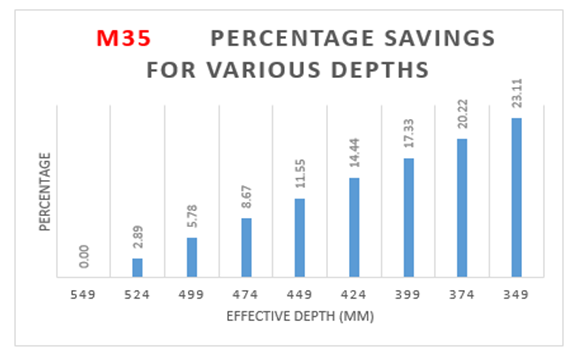 | Figure 5(c). Variation of percentage savings for M35 Grade Concrete |
Case 2: i) Span of size 12600 mm x12600 mmGrade of concrete=M25Cost of concrete = Rs.9000 per CumCost of steel = Rs.60000 per MTCost of formwork= Rs.400 per SqmTable 4. Parameters of the Ribbed Slab for M25 Grade Concrete – 12600 mm x 12600 mm
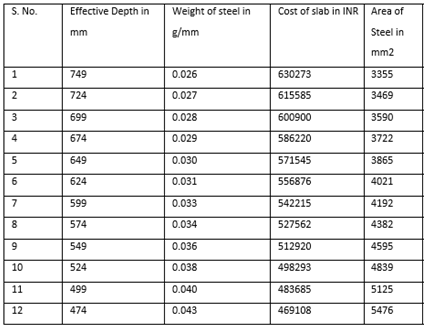 |
| |
|
From the above Table 4:, for M25 grade of concrete, it is observed that area of steel is increasing by 63 percent with decrease in effective depth.Also from Figure 6(a):, the weight of steel is increasing by 65 percent with decrease in effective depth.The cost of the slab is increasing by 34 percent with increase in effective depth as observed from Figure 6(b):.The optimum point here is observed to be 474 mm (effective depth) as it results in savings of 25.76% over normal design.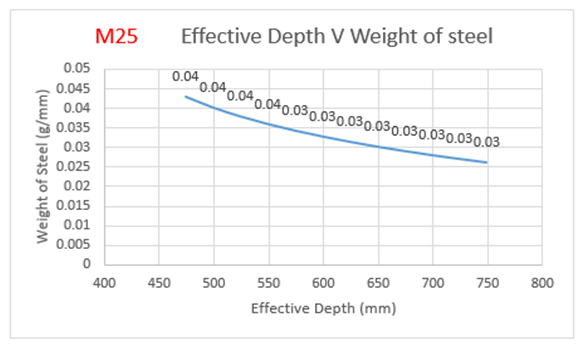 | Figure 6(a). Variation of effective depth to weight of steel for M25 Concrete Grade |
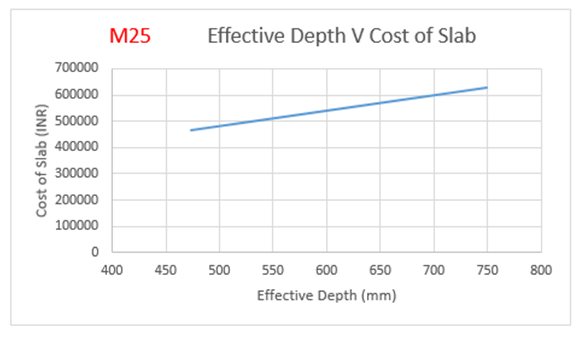 | Figure 6(b). Variation of effective depth to cost of slab for M25 Concrete Grade |
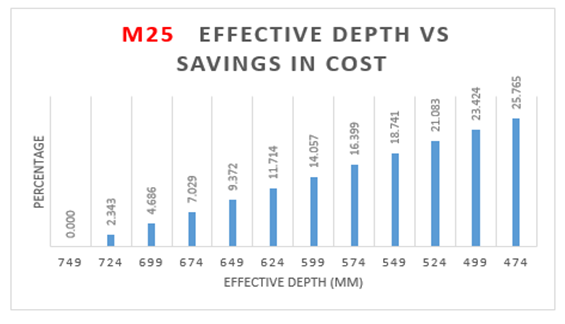 | Figure 6(c). Variation of effective depth to savings in cost for M25 Concrete Grade |
Case 2: ii) Span of size 12600 mm x 12600 mmGrade of concrete=M30Cost of concrete = Rs.10000 per CumCost of steel = Rs.60000 per MTCost of formwork= Rs.400 per SqmTable 5. Parameters of the Ribbed Slab for M30 Grade Concrete – 12600 mm x 12600 mm
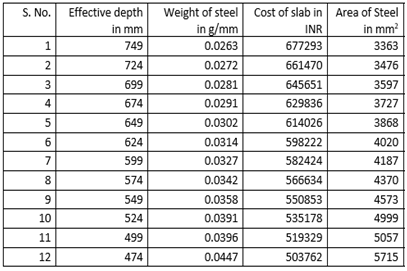 |
| |
|
From Table 5:, for M30 grade of concrete, it is observed that area of steel is increasing by 69 percent with decrease in effective depth. Also from Figure 7(a):, the weight of steel is increasing by 70 percent with decrease in effective depth. The cost of the slab is increasing by 34 percent with increase in effective depth as observed from Figure 7(b):.The optimum point here is observed to be 474 mm (effective depth) as it results in savings of 25.82% over normal design.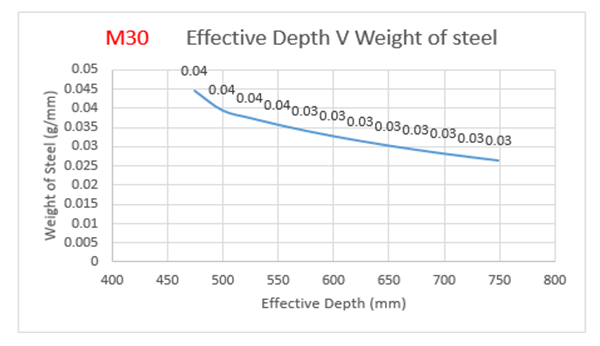 | Figure 7(a). Variation of effective depth to weight of steel for M30 Concrete Grade |
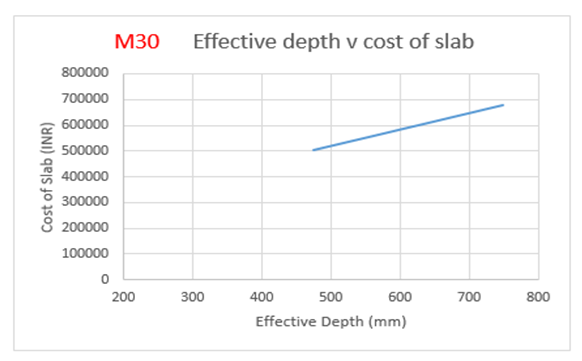 | Figure 7(b). Variation of effective depth to cost of slab for M30 Concrete Grade |
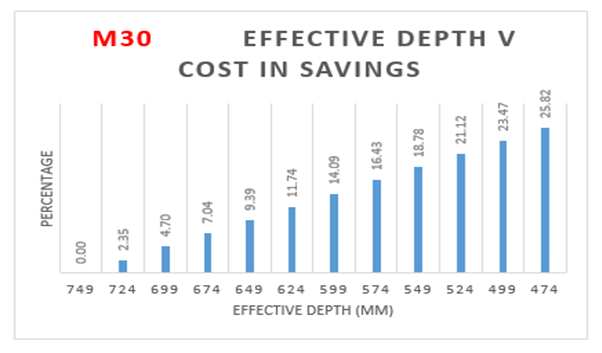 | Figure 7(c). Variation of effective depth to cost savings for M30 Concrete Grade |
Case 2: iii) Span of size 21000 mm x 21000 mmGrade of concrete=M35Cost of concrete = Rs.10500 per CumCost of steel = Rs.60000 per MTCost of formwork= Rs.400 per SqmTable 6. Parameters of the Ribbed Slab for M35 Grade Concrete – 12600 mm x 12600 mm
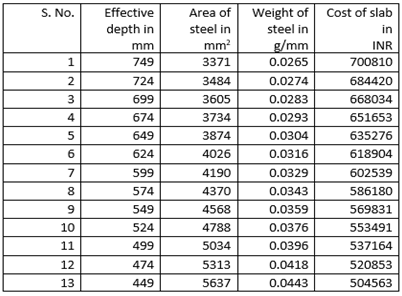 |
| |
|
From Table 6:, for M35 grade of concrete, it is observed that area of steel is increasing by 67 percent with decrease in effective depth. Also from Figure 8(a), the weight of steel is increasing by 67 percent with decrease in effective depth. 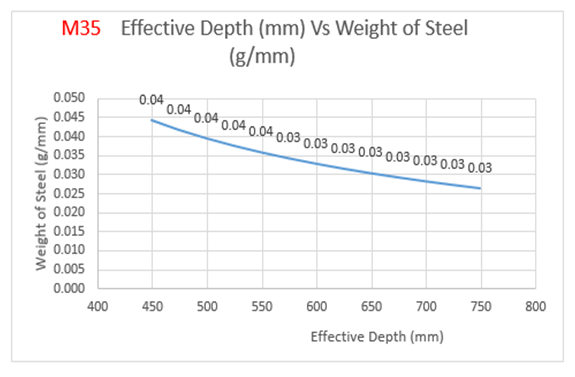 | Figure 8(a). Variation of effective depth to weight of steel for M35 Concrete Grade |
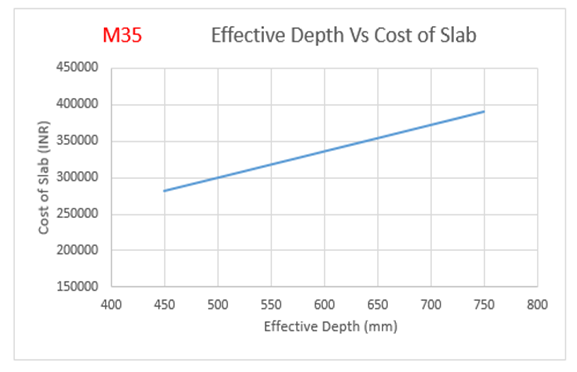 | Figure 8(b). Variation of effective depth to cost of slab for M35 Concrete Grade |
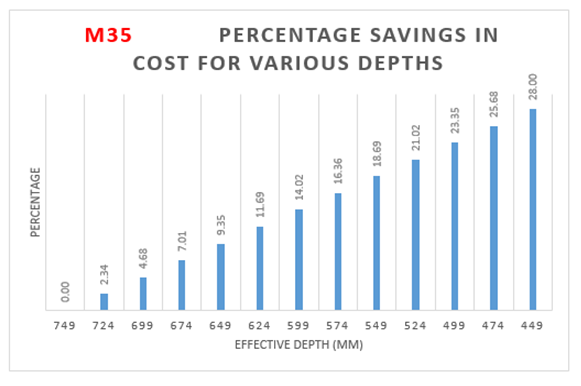 | Figure 8(c). Variation of percentage of savings to cost of varying depths |
The cost of the slab is increasing by 38 percent with increase in effective depth as observed from Figure 8(b):The optimum point here is observed to be 449 mm (effective depth) as it results in savings over normal design.Case 3: i) Span of size 21000 mm x 21000 mmGrade of concrete=M30Cost of concrete = Rs.10500 per CumCost of steel = Rs.60000 per MTCost of formwork= Rs.400 per SqmTable 7. Parameters of the Ribbed Slab for M30 Grade Concrete – 21000 mm x 21000 mm
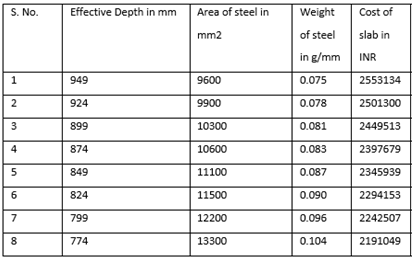 |
| |
|
From the above Table 7:, for M30 grade of concrete, it is observed that area of steel is increasing by 39 percent with decrease in effective depth. Also from Figure 9(a):, the weight of steel is increasing by 39 percent with decrease in effective depth. The cost of the slab is increasing by 17 percent with increase in effective depth as observed from Figure 9(b):The optimum point here is observed to be 774 mm (effective depth) as it results in savings of 14.18% over normal design.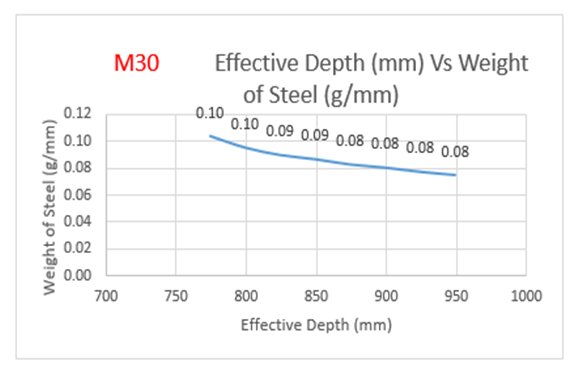 | Figure 9(a). Variation of effective depth to weight of steel for M30 Concrete Grade |
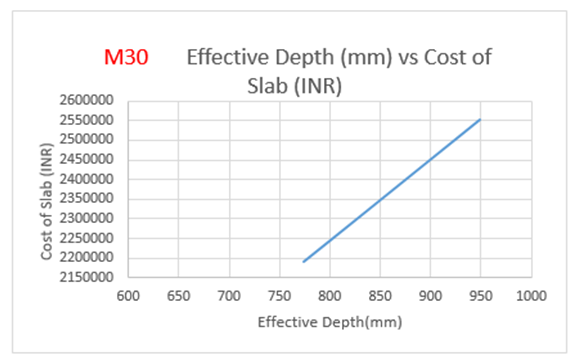 | Figure 9(b). Variation of effective depth to cost of slab for M30 Concrete Grade |
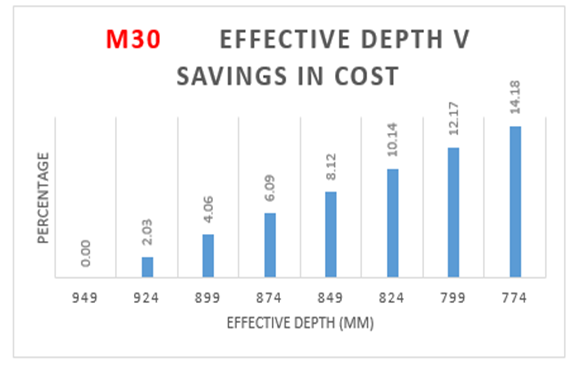 | Figure 9(c). Variation of effective depth to savings in cost for M30 Concrete Grade |
Case 3: ii) Span of size 21000 mm x 21000 mm Grade of concrete=M35Cost of concrete = Rs.10500 per CumCost of steel = Rs.60000/MTCost of formwork= Rs.400 per Sqm.Table 8. Parameters of the Ribbed Slab for M25 Grade Concrete – 21000 mm x 21000 mm
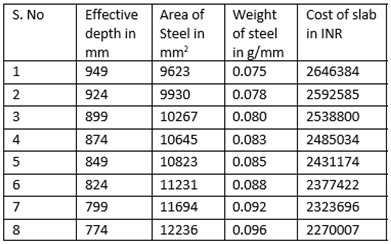 |
| |
|
From the above Table 8:, for M35 grade of concrete, it is observed that area of steel is increasing by 27 percent with decrease in effective depth. Also from Figure 10(a):, the weight of steel is increasing by 28 percent with decrease in effective depth. The cost of the slab is increasing by 16.5 percent with increase in effective depth as observed from Figure10 (b):The optimum point here is observed to be 774 mm (effective depth) as it results in savings of 14.25 % over normal design.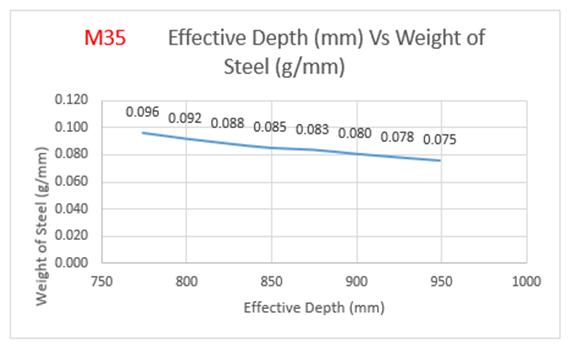 | Figure 10(a). Variation of effective depth to weight of steel for M35 Concrete Grade |
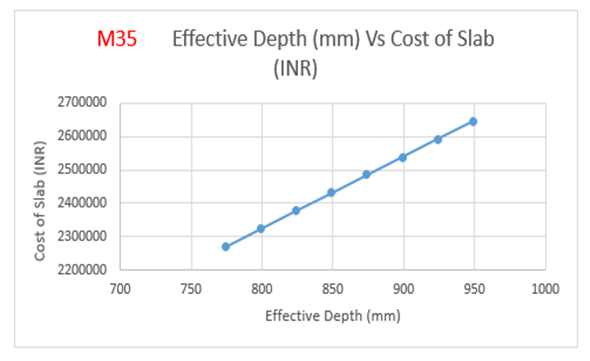 | Figure 10(b). Variation of effective depth to cost of slab for M35 Concrete Grade |
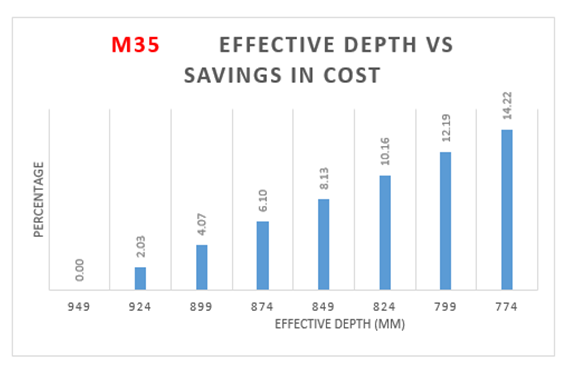 | Figure 10(c). Variation of effective depth to savings in cost for M35 Concrete Grade |
ComparisonCase 1: Slab of size 10000 mm x 10000 mm 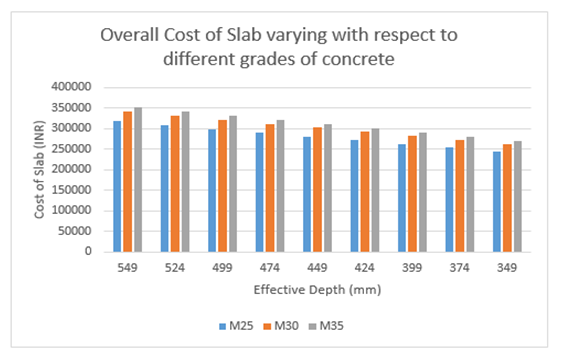 | Figure 11. Cost of slab Vs different grades of concrete |
Figure 11, shows the graphical representation cost values for ribbed slab for different grades of concrete.M30 grade of concrete shows 7 percent increase in overall cost over M25 whereas M35 shows 11 percent increase.Case 2: Slab of size 12600 mm x 12600 mm 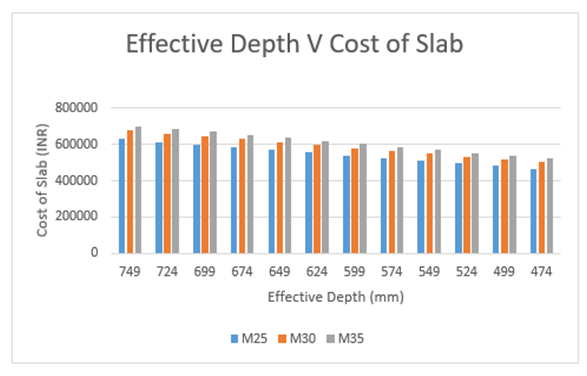 | Figure 12. Effective depth Vs cost of slab for various grades of concrete |
The overall cost of the slab increases as the grade of concrete increases.Case 3: Span of size 21000 mm x 21000 mm 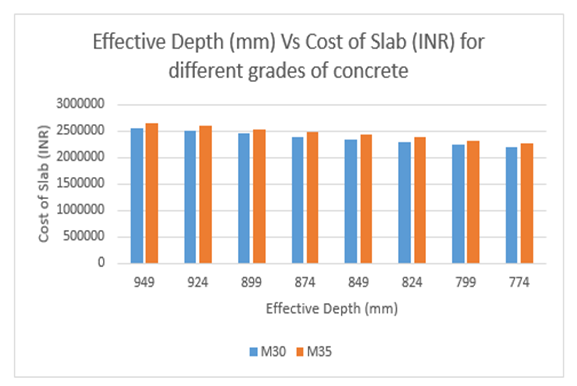 | Figure 13. Effective depth Vs cost of slab for various grades of concrete |
M35 grade of concrete shows 4 percent increase in overall cost over M30.Depths for different spans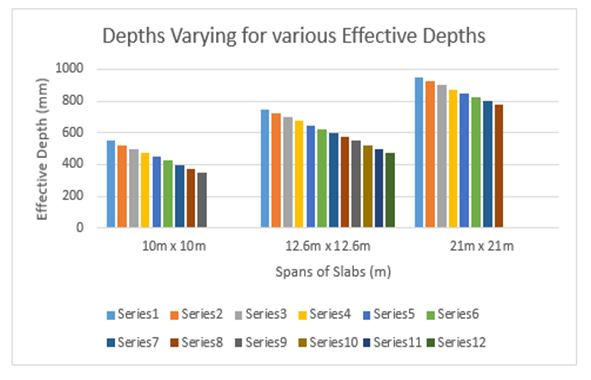 | Figure 14. Variation of effective depths with spans |
Figure 14: shows that the effective depth increases with increase in span for 12600 mm x 12600 mm span. Further, it is observed that 36 percent increase in depth over 10000 mm x 10000 mm span and 21000 mm x 21000 mm span shows 26 percent increase in depth over 12600 mm x 12600 mm span.
6. Conclusions
1. It is possible to formulate and obtain the optimum design of a ribbed slab by optimizing the effective depth and the percentage of reinforcement within the codal provisions, complying to the minimum depth and the minimum percentage of steel. 2. Maximum cost savings of 22.71%, 22.80% and 23.11% can be obtained over the normal design in case of ribbed slab with 10000 mm x 10000 mm span for M25, M30 and M35 grades of concrete respectively.3. Cost savings of 25.57%, 25.62% and 25.71% are obtained in case of ribbed slab with 12600 mm x 12600 mm span for M25, M30 and M35 grades of concrete respectively. 4. The overall cost of the ribbed slab increases by as much as 39 percent as the depth of slab increases. 5. The overall cost of the ribbed slab is directly proportional to depth of the slab and inversely proportional to the area and the weight of the steel.6. As the panel size of the ribbed slab increases, the depth of the slab increases, consequently the cost of the ribbed slab also increases. 7. Ribbed slab of span 10000 mm x 10000 mm shows 26 percent increase in depth over 12600 mm x 12600 mm span whereas 12600 m x 12600 mm span shows 36 percent increase in depth over 21000 mm x 21000 mm span.
ACKNOWLEDGEMENTS
The authors’ wishes to thank CHRIST (Deemed to be University) for the facility and the resources provided for conducting the research.
References
| [1] | Galeb. A. C and Atiyah Z. F, “Optimum design of reinforced concrete waffle slabs”, International Journal of civil and structural Engineering, Volume 1, No 4, 2014. |
| [2] | Patil K, Salunke. P. J, “Optimum design of reinforced concrete flat slab with drop panel”, International Journal of Recent Technology and Engineering, ISSN: 2277-3878 Volume-2, Issue-4, September 2013. |
| [3] | Sathawane. A. A and Deotale R. S, “Analysis and design of flat slab and grid slab and their cost comparison,” International Journal of Engineering Research and Applications, ISSN: 2248-9622 Volume-1, Issue-3, pp: 837-848, September 2012. |
| [4] | Kaveh. A and Zakian. P, "Performance based optimal seismic design of RC shear wall incorporating soil structural interaction using CSS algorithm” Iran university of science and technology, ISSN: 383-405 Volume-2, Issue-3, July 2012. |
| [5] | Kushwaha. B. K, N.G. Kishore. N. G and Salunke. P. J “Optimization of PSC slab bridges," International Journal of Recent Technology and Engineering (IJRTE), ISSN:: 2277-3878, Volume-3, Issue-2, 2014. |
| [6] | Atabay. S "Cost optimization of three-dimensional beamless reinforced concrete shear wall systems via genetic algorithm" Expert Systems with Applications, Volume-36, Issue-2, pp: 3555-3561, March 2009. |
| [7] | Jinjie. M and Qingxuan. S, “Optimal design of tall residential building with R.C. Shear wall and with rectangular layout “International journal of high rise buildings”, Volume-3, Issue-4, pp:285-296, December 2014. |
| [8] | Kaveh. A and Behnam.A. F, “Optimum cost design of reinforced concrete one way ribbed slabs using CBO, PSO and democratic PSO algorithms" Asian Journal Of Civil Engineering, Volume-15, Issue-6, pp:788-802, 2014. |
| [9] | Subramanian, N, “Design of Reinforced Concrete Structures” Oxford University Press, New Delhi, 2013. |
| [10] | IS 456:2000: Plain Reinforced Concrete Structures. Bureau of Indian Standards, New Delhi, 2000. |
| [11] | http://www.wolfram.com/mathematic/. |





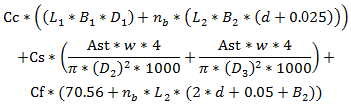 Where,Cc is the cost of the concreteCs is the cost of the steelCf is the cost of the formworkL1 is the length of the SlabL2 is the length of the beamB1 is the breadth of the slabB2 is the breadth of the beamD1 is the depth of the topping slabD2 and D3 are the diameters of the reinforcement barsNb is the number of ribsAst is the area of steel25mm is the cover for beamsw is the unit weight of the reinforcement bard is the effective depth of the beam
Where,Cc is the cost of the concreteCs is the cost of the steelCf is the cost of the formworkL1 is the length of the SlabL2 is the length of the beamB1 is the breadth of the slabB2 is the breadth of the beamD1 is the depth of the topping slabD2 and D3 are the diameters of the reinforcement barsNb is the number of ribsAst is the area of steel25mm is the cover for beamsw is the unit weight of the reinforcement bard is the effective depth of the beam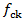 = characteristic compressive strength of concrete.Cost of the slab.
= characteristic compressive strength of concrete.Cost of the slab.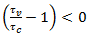
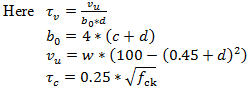 2. Minimum depth constraint:
2. Minimum depth constraint: 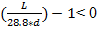 Where,
Where,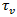 is the nominal shear stress
is the nominal shear stress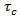 is the permissible shear stress
is the permissible shear stress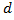 is the design variable, effective depth
is the design variable, effective depth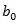 is the width of solid head of the slab
is the width of solid head of the slab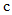 is the width of solid portion of the slab
is the width of solid portion of the slab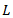 is the span of slab in both directions
is the span of slab in both directions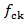 is the characteristic compressive strength of concrete.w is the factored load acting on the slab
is the characteristic compressive strength of concrete.w is the factored load acting on the slab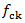 = Characteristic Compressive Strength of concrete = M25, M30fy = Characteristic Strength of steel = Fe 415Cost of Concrete: M25 = Rs.9000 per CumM30 = Rs.10000 per CumM35 = Rs.10500 per CumCost of Steel:Fe415 = Rs.60000 per Metric TonneCost of Formwork = Rs.400 per SqmSlab of sizes of 10000 mm x 10000 mm, 12600 mm x 12600 mm and 21000 mm x 21000 mm are considered in the research.
= Characteristic Compressive Strength of concrete = M25, M30fy = Characteristic Strength of steel = Fe 415Cost of Concrete: M25 = Rs.9000 per CumM30 = Rs.10000 per CumM35 = Rs.10500 per CumCost of Steel:Fe415 = Rs.60000 per Metric TonneCost of Formwork = Rs.400 per SqmSlab of sizes of 10000 mm x 10000 mm, 12600 mm x 12600 mm and 21000 mm x 21000 mm are considered in the research.



























 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML






