-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2019; 9(2): 43-50
doi:10.5923/j.jce.20190902.01

A Stochastic Multicriteria Algorithm for Generating Waste Management Facility Expansion Alternatives
Julian Scott Yeomans
OMIS Area, Schulich School of Business, York University, Toronto, Canada
Correspondence to: Julian Scott Yeomans, OMIS Area, Schulich School of Business, York University, Toronto, Canada.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

While solving waste management (WM) planning problems, it may often be preferable to generate several quantifiably good options that provide multiple, contrasting perspectives. This is because WM planning generally contains complex problems that are riddled with inconsistent performance objectives and contain design requirements that are very difficult to quantify and capture when supporting decision models must be constructed. The generated alternatives should satisfy all of the stated system conditions, but be maximally different from each other in the requisite decision space. The process for creating maximally different sets of solutions is referred to as modelling-to-generate-alternatives (MGA). Simulation-optimization approaches have frequently been used to solve computationally difficult, stochastic WM problems. This paper outlines a stochastic multicriteria MGA approach for WM planning that can generate sets of maximally different alternatives for any simulation-optimization method that employs a population-based solution algorithm. This algorithmic approach is computationally efficient because it simultaneously produces the prescribed number of maximally different solution alternatives in a single computational run of the procedure. The efficacy of this stochastic MGA method is demonstrated on a “real world” waste management facility expansion case.
Keywords: Modelling-to-generate-alternatives, Simulation-optimization, Waste management planning, Population-based algorithms
Cite this paper: Julian Scott Yeomans, A Stochastic Multicriteria Algorithm for Generating Waste Management Facility Expansion Alternatives, Journal of Civil Engineering Research, Vol. 9 No. 2, 2019, pp. 43-50. doi: 10.5923/j.jce.20190902.01.
Article Outline
1. Introduction
- Implementing effective management of waste management (WM) systems has often proven to be contentious and conflict-laden ([1-3]). Since WM systems generally contain all of the characteristics associated with complex planning situations, waste management problems have provided an ideal backdrop for the testing of an extensive assortment of decision support techniques used for decision-making ([3-6]). Stochastic decision-making typically contains complex design aspects that can be problematic to integrate into mathematical formulations and can be inundated by unquantifiable specifications ([4-6]). WM decision-making frequently possess inconsistent and incompatible design specifications that can be difficult to formulate into supporting mathematical decision-models ([6]). This situation commonly occurs when final decisions must be constructed based not only upon clearly articulated specifications, but also upon environmental, political and socio-economic objectives that are either fundamentally subjective or not clearly articulated ([7-10]). Although “optimal” solutions to the modelled constructions can be determined, these do not usually deliver the best solution to the “real” problem as there are generally unmodeled components not apparent when the mathematical models are created ([1,2,9]). Moreover, it may not be possible to explicitly convey many of the subjective components because there are numerous competing, adversarial stakeholder groups holding diametrically opposed perspectives. Therefore, many of the subjective aspects remain unknown, unquantified and unmodelled in the construction of the corresponding decision models. WM policy formulation can prove even more complicated when the various system components also contain stochastic uncertainties ([11]). Consequently, waste management determination proves to be an extremely challenging and complicated endeavour ([11,12]).Within WM decision-making, there are routinely many stakeholder groups possessing incongruent standpoints, essentially dictating that the waste managers need to build decision frameworks that simultaneously reflect numerous irreconcilable points of view ([4]). As a result, it is more desirable to construct a small number of dissimilar alternatives that permit opposing perspectives to the stated problem ([4,10]). These options should be close-to-optimal with respect to all identified objective(s), but be maximally different from each other in the decision region. The formal process for creating such maximally different solution sets is usually referred to as modelling-to-generate-alternatives (MGA) ([8-10]). MGA techniques prescribe a systematic examination of the solution space in order to create a set of alternatives that are considered good when measured by the objective space but as different as possible from each other in the modelled decision space. The resultant solution set should provide alternative viewpoints that perform similarly with respect to the modelled objectives, yet very differently with respect to any potentially unmodelled features ([6]). Subsequently, the decision-makers must perform a comparison of the alternatives to determine which option(s) most closely achieve(s) their specific requirements. In comparison to the more straightforward solution determination approaches inherent in most “traditional” optimization methods, MGA approaches fall necessarily into the decision support category.Early MGA algorithms employed direct, incremental approaches for constructing their alternatives by iteratively re-running their procedures whenever new solutions needed to be generated ([7-11]). These iterative approaches replicated the seminal MGA work of [8] where, once the initial mathematical formulation has been optimized, all supplementary alternatives are produced one-at-a-time. These approaches all required n+1 iterations of their algorithms – to optimize the original problem in the first step, followed by the subsequent sequential construction of each of the n alternatives ([10,12-14]).In this paper, it is shown how the set of maximally different options can be created by extending several earlier deterministic MGA approaches to stochastic optimization ([13-19]). The stochastic algorithm provides an MGA process that can be performed by any population-based solution mechanism. This algorithm advances earlier procedures ([14-18]) to permit the generation of n distinct alternatives simultaneously in a single computational run. Namely, in order to generate n maximally different alternatives, the algorithm runs exactly the same number of times that a function optimization procedure needs to run (i.e. once) irrespective of the value of n ([20-24]). Furthermore, a multicriteria objective is employed that combines a novel data structure into the simultaneous solution approach to create an effective MGA approach. This data structure facilitates the above-mentioned solution generalization to population-based methods. Consequently, this stochastic multicriteria MGA algorithmic approach proves to be very computationally efficient ([25]). The procedure is demonstrated on a WM facilities expansion case that had previously been considered in ([26-28]).
2. Modelling to Generate Alternatives
- Mathematical optimization has fixated almost entirely on determining single optimal solutions to single-objective problems or constructing sets of noninferior solutions for multi-objective formulations ([2,6,8]). While these approaches may provide solutions to the formal mathematical models, whether these outputs are truly the best solutions to the “real” problems remains can be debatable ([1,2,8,9]). Within most “real world” decision-making environments, there are countless system requirements and objectives that will never be explicitly apparent or included in the model formulation stage ([1,6]). Furthermore, most subjective aspects remain unavoidably unmodelled and unquantified in the constructed decision models. This regularly occurs where final decisions are constructed based not only on modelled objectives, but also on more subjective stakeholder goals and socio-political-economic preferences ([10]). Several incongruent modelling dualities are discussed in ([7-9,11]).When unmodelled objectives and unquantified issues exist, non-traditional methods are required for searching the decision region not only for noninferior sets of solutions, but also for alternatives that are evidently sub-optimal to the modelled problem. Namely, any search for alternatives to problems known or suspected to contain unmodelled components must concentrate not only on a non-inferior set of solutions, but also necessarily on an explicit exploration of the problem’s inferior solution space.To demonstrate the consequences of an unmodelled objective in a decision search, assume that the quantifiably optimal solution for a single-objective, maximization problem is X* with a corresponding objective value Z1*. Now suppose that a second, unmodelled, maximization objective Z2 exists that subjectively incorporates some unquantifiable “politically acceptable” component. Now assume that some solution, Xa, belonging to the 2-objective noninferior set, exists that represents a potentially best compromise solution for the decision-maker if both objectives had somehow been simultaneously evaluated. While Xa could reasonably be considered as the best compromise solution for the real problem, in the quantified mathematical model it would appear inferior to solution X*, since it must be the case that Z1a≤Z1*. Therefore, when unmodelled components are incorporated into a decision-making process, mathematically inferior options to the modelled problem could actually be optimal for the real underlying problem. By creating these good-but-different solutions, the decision-makers can then examine potentially desirable qualities within the options that may be able to address potentially unmodelled objectives to varying degrees of stakeholder tolerability.To motivate the MGA process, it is necessary to more formally characterize the mathematical definition of its goals ([9], [10]). Assume that the optimal solution to an original mathematical model is X* with corresponding objective value Z* = F(X*). The resultant difference model can then be solved to produce an alternative solution, X, that is maximally different from X*:
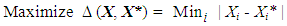 | (1) |
 | (2) |
 | (3) |
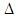 represents an appropriate difference function (shown in (1) as an absolute difference) and T is a tolerance target relative to the original optimal objective value Z*. T is a user-specified limit that determines what proportion of the inferior region needs to be explored for acceptable alternatives. This difference function concept can be extended into a difference measure between any set of alternatives by replacing X* in the objective of the maximal difference model and calculating the overall minimum absolute difference (or some other function) of the pairwise comparisons between corresponding variables in each pair of alternatives – subject to the condition that each alternative is feasible and falls within the specified tolerance constraint.The population-based MGA procedure to be introduced is designed to generate a pre-determined small number of close-to-optimal, but maximally different alternatives, by adjusting the value of T and solving the corresponding maximal difference problem instance by exploiting the population structure of the metaheuristic. The survival of solutions depends upon how well the solutions perform with respect to the problem’s originally modelled objective(s) and simultaneously by how far away they are from all of the other alternatives generated in the decision space.
represents an appropriate difference function (shown in (1) as an absolute difference) and T is a tolerance target relative to the original optimal objective value Z*. T is a user-specified limit that determines what proportion of the inferior region needs to be explored for acceptable alternatives. This difference function concept can be extended into a difference measure between any set of alternatives by replacing X* in the objective of the maximal difference model and calculating the overall minimum absolute difference (or some other function) of the pairwise comparisons between corresponding variables in each pair of alternatives – subject to the condition that each alternative is feasible and falls within the specified tolerance constraint.The population-based MGA procedure to be introduced is designed to generate a pre-determined small number of close-to-optimal, but maximally different alternatives, by adjusting the value of T and solving the corresponding maximal difference problem instance by exploiting the population structure of the metaheuristic. The survival of solutions depends upon how well the solutions perform with respect to the problem’s originally modelled objective(s) and simultaneously by how far away they are from all of the other alternatives generated in the decision space. 3. Simulation-Optimization for Stochastic Optimization
- Finding optimal solutions to large stochastic problems proves complicated when numerous system uncertainties must be directly incorporated into the solution procedures ([29-32]). Simulation-Optimization (SO) refers to a family of stochastic solution approaches that combines simulation with an underlying optimization component for optimization ([29]). In SO, all unknown objective functions, constraints, and parameters are replaced by simulation models in which the decision variables provide the settings under which simulation is performed.The general steps of SO can be summarized in the following fashion ([31,33]). Suppose the mathematical model of the optimization problem contains n decision variables,
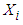 , represented in the vector
, represented in the vector 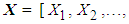
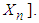 If the objective function is expressed by F and the feasible region is designated by D, then the mathematical programming problem is to optimize F(X) subject to
If the objective function is expressed by F and the feasible region is designated by D, then the mathematical programming problem is to optimize F(X) subject to 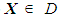 . When stochastic conditions exist, values for the objective and constraints can be determined by simulation. Any solution comparison between two different solutions X1 and X2 requires the evaluation of some statistic of F modelled with X1 compared to the same statistic modelled with X2 ([29,34]). These statistics are calculated by simulation, in which each X provides the decision variable settings employed in the simulation. While simulation provides a means for comparing results, it does not provide the mechanism for determining optimal solutions to problems. Hence, simulation cannot be used independently for stochastic optimization.Since all measures of system performance in SO are stochastic, every potential solution, X, must be calculated through simulation. Because simulation is computationally intensive, an optimization algorithm is employed to guide the search for solutions through the problem’s feasible domain in as few simulation runs as possible ([32,34]). As stochastic system problems frequently contain numerous potential solutions, the quality of the final solution could be highly variable unless an extensive search has been performed throughout the entire feasible region. A stochastic SO approach contains two alternating computational phases; (i) an “evolutionary” module directed by some optimization (frequently a metaheuristic) method and (ii) a simulation module ([35]). Because of the stochastic components, all performance measures are necessarily statistics calculated from the responses generated in the simulation module. The quality of each solution is found by having its performance criterion, F, evaluated in the simulation module. After simulating each candidate solution, their respective objective values are returned to the evolutionary module to be utilized in the creation of ensuing candidate solutions. Thus, the evolutionary module aims to advance the system toward improved solutions in subsequent generations and ensures that the solution search does not become trapped in some local optima. After generating new candidate solutions in the evolutionary module, the new solution set is returned to the simulation module for comparative evaluation. This alternating, two-phase search process terminates when an appropriately stable system state (i.e. an optimal solution) has been attained. The optimal solution produced by the procedure is the single best solution found throughout the course of the entire search process ([35]).Population-based algorithms are conducive to SO searches because the complete set of candidate solutions maintained in their populations permit searches to be undertaken throughout multiple sections of the feasible region, concurrently. For population-based optimization methods, the evolutionary phase evaluates the entire current population of solutions during each generation of the search and evolves from a current population to a subsequent one. A primary characteristic of population-based procedures is that better solutions in a current population possess a greater likelihood for survival and progression into the subsequent population.It has been shown that SO can be used as a very computationally intensive, stochastic MGA technique ([34,36]). However, because of the very long computational runs, several approaches to accelerate the search times and solution quality of SO have been examined subsequently ([33]). The next section provides an MGA algorithm that incorporates stochastic uncertainty using SO to much more efficiently generate sets of maximally different solution alternatives.
. When stochastic conditions exist, values for the objective and constraints can be determined by simulation. Any solution comparison between two different solutions X1 and X2 requires the evaluation of some statistic of F modelled with X1 compared to the same statistic modelled with X2 ([29,34]). These statistics are calculated by simulation, in which each X provides the decision variable settings employed in the simulation. While simulation provides a means for comparing results, it does not provide the mechanism for determining optimal solutions to problems. Hence, simulation cannot be used independently for stochastic optimization.Since all measures of system performance in SO are stochastic, every potential solution, X, must be calculated through simulation. Because simulation is computationally intensive, an optimization algorithm is employed to guide the search for solutions through the problem’s feasible domain in as few simulation runs as possible ([32,34]). As stochastic system problems frequently contain numerous potential solutions, the quality of the final solution could be highly variable unless an extensive search has been performed throughout the entire feasible region. A stochastic SO approach contains two alternating computational phases; (i) an “evolutionary” module directed by some optimization (frequently a metaheuristic) method and (ii) a simulation module ([35]). Because of the stochastic components, all performance measures are necessarily statistics calculated from the responses generated in the simulation module. The quality of each solution is found by having its performance criterion, F, evaluated in the simulation module. After simulating each candidate solution, their respective objective values are returned to the evolutionary module to be utilized in the creation of ensuing candidate solutions. Thus, the evolutionary module aims to advance the system toward improved solutions in subsequent generations and ensures that the solution search does not become trapped in some local optima. After generating new candidate solutions in the evolutionary module, the new solution set is returned to the simulation module for comparative evaluation. This alternating, two-phase search process terminates when an appropriately stable system state (i.e. an optimal solution) has been attained. The optimal solution produced by the procedure is the single best solution found throughout the course of the entire search process ([35]).Population-based algorithms are conducive to SO searches because the complete set of candidate solutions maintained in their populations permit searches to be undertaken throughout multiple sections of the feasible region, concurrently. For population-based optimization methods, the evolutionary phase evaluates the entire current population of solutions during each generation of the search and evolves from a current population to a subsequent one. A primary characteristic of population-based procedures is that better solutions in a current population possess a greater likelihood for survival and progression into the subsequent population.It has been shown that SO can be used as a very computationally intensive, stochastic MGA technique ([34,36]). However, because of the very long computational runs, several approaches to accelerate the search times and solution quality of SO have been examined subsequently ([33]). The next section provides an MGA algorithm that incorporates stochastic uncertainty using SO to much more efficiently generate sets of maximally different solution alternatives.4. Multicriteria Population-based Simultaneous MGA Computational Algorithm
- In this section, a novel data structure is employed that enables a multicriteria MGA solution approach via any population-based algorithm ([25,37,38]). Suppose that it is desired to be able to produce P alternatives that each possess n decision variables and that the population algorithm is to possess K solutions in total. That is, each solution is to contain one possible set of P maximally different alternatives. In this representation, let Yk, k = 1,…, K, represent the kth solution which is made up of one complete set of P different alternatives. Namely, if Xkp is the pth alternative, p = 1,…, P, of solution k, k = 1,…, K, then Yk can be represented as
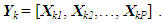 | (4) |
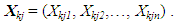 | (5) |
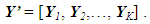 | (6) |
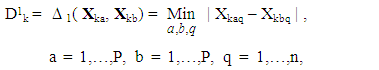 | (7) |
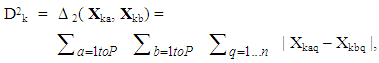 | (8) |
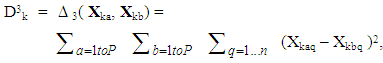 | (9) |
5. Waste Facility Expansion Case Study
- As mentioned earlier, “real world” decision-makers often prefer to choose from a set of “close-to-optimal” options that differ significantly from each other in terms of the structures represented in their decision variables. The capacity of the stochastic multicriteria MGA procedure to produce a set of maximally different alternatives concurrently will be demonstrated using the MSW expansion planning case previously considered in ([26,27,28]).The region in this facility expansion problem contains three separate municipalities whose MSW disposal needs are collectively met by a landfill and two waste-to-energy (WTE) incinerators. The planning horizon consists of three separate time periods with each of the periods covering an interval of five years. The landfill capacity can only be expanded once throughout the 15-year planning horizon. Each WTE facility can be expanded by any one of four possible options in each of the three time periods. The expansion costs escalate over time to reflect anticipated future conditions and have been discounted to present values for use in the objective function. The MSW waste generation rates and the costs for waste transportation and treatment vary both spatially and temporally. The case requires the construction of the preferred facility expansion alternatives during the different time periods and the effective allocation of the relevant waste flows in order to minimize the total system costs over the planning horizon.A single best solution to the expansion problem costing $600.2 million was determined in Yeomans (2012a). However, as discussed, planners generally prefer to be able to select from a set of close-to-optimal alternatives that differ significantly from each other in terms of the system structures characterized by their decision variables. In order to create three alternative planning options, it would be possible to place extra target constraints into the maximal difference model which would force the generation of solutions that were different from this newly determined, optimal solution by target values of, for example, 2.5%, 5%, and 7.5%, respectively. By adding these specific target constraints to the original model, the problem would need to be resolved an additional three times. However, to improve upon the process of running four separate instances of the SO algorithm to determine these solutions, the stochastic population-based multicriteria MGA procedure described in the previous section was run once to produce the objectives for the 4 alternatives shown in Table 1. To illustrate the solution variety created by the MGA procedure, Table 2 displays the system expansion costs of the sets of 4 alternatives for each of the top 15 solutions remaining in the final population.
|
|
6. Conclusions
- Waste management problems contain multifaceted performance specifications which inevitably possess incongruent performance objectives and unquantifiable modelling features. These decision environments frequently contain incompatible design provisions that are problematic – if not impossible – to incorporate when ancillary decision support models are constructed. Invariably, there are unmodelled elements, not apparent during model formulation, that can significantly affect the adequacy of its solutions. These competing and ambiguous components force WM decision-makers to incorporate many conflicting requirements into their decision process prior to the final solution determination. Consequently, waste management decision-makers generally prefer to select from a set of distinct planning perspectives.This paper has employed a computationally efficient multicriteria approach for waste facility expansion planning using any population-based solution algorithm. This computationally efficient approach establishes how population-based algorithms can simultaneously construct entire sets of close-to-optimal, maximally different alternatives by exploiting the evolutionary characteristics of any population-based solution method. This MGA algorithm establishes how population-based methods can simultaneously construct entire sets of near-optimal, maximally different alternatives by exploiting the evolving solution characteristics in population-based solution approaches. In an MGA role, a multicriteria objective can efficiently generate the requisite set of dissimilar alternatives, with each generated solution suggesting an entirely different perspective to the problem. The practicality of this stochastic multicriteria MGA approach can be readily extended into numerous disparate applications and can be clearly modified to suit many “real world” planning situations. Such extensions will be explored in future research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML