Zhirong Xiao, Zhengwei Zhang, Anthony Quansah
School of Civil Engineering, Zhejiang University of Science and Technology, Zhejiang Province, China
Correspondence to: Zhirong Xiao, School of Civil Engineering, Zhejiang University of Science and Technology, Zhejiang Province, China.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Under the condition of unknown real value of the mechanical model, effective and accurate identification of the mechanical parameters of the magnetorheological damper model has been an urgent problem in the field of civil engineering vibration control. In this paper, the ant colony optimization algorithm(ACO) and the unscented Kalman filter algorithm(UKF) are used to identify the parameters in Bingham model and Bouc-Wen model of MR damper. Experiments show that the ACO algorithm based on meshing can provide better initial values for the UKF algorithm, and the accuracy of the model identified by this numerical value is high, and the matching of the characteristic curve is also satisfied.
Keywords:
The ant colony optimization algorithm, The unscented Kalman filter algorithm, Combined identification, Magnetorheological damper
Cite this paper: Zhirong Xiao, Zhengwei Zhang, Anthony Quansah, Combined Identification of Parameters in the Mechanical Model of Magnetorheological Damper, Journal of Civil Engineering Research, Vol. 9 No. 1, 2019, pp. 16-24. doi: 10.5923/j.jce.20190901.02.
1. Introduction
Magnetorheological damper (MRD) is a semi-active control device with high cost performance and engineering application prospect. However, due to the shear thinning of MRF in MR dampers, it has strong non-linearity, which limits the application of MR dampers. How to effectively identify the parameters in the mechanical model of MR damper has become a research hotspot. Zhou Xiaohong et al. [1] studied the optimization of parameters in modified Bouc-Wen model by genetic algorithm. The results show that the relative error between the identified parameters and the actual values is large. Priya et al. [2] proposed using the non-linear least squares method to identify unknown parameters in Bouc-Wen model, and obtained the specific relationship between parameters and functions. However, this method needs some experience, and the recognition accuracy is not high. Ant Colony Optimization (ACO) algorithm has low accuracy and UKF algorithm has high accuracy, but it depends on the initial conditions. In this paper, ant colony optimization (ACO) algorithm is used to provide the initial value for unscented Kalman filter (UKF), and two methods are combined to solve the problem of parameter identification of MR damper mechanical model.
2. Mechanical Model
(1) Bingham ModelBingham’s model is the most widely studied model in the mechanical model of MR damper. It was first used by Phillips [3] and others to reflect the stress-strain relationship of magnetorheological fluids under stable shear field. After improvement by Stanway [4], it has become the Bingham model of MR damper. Its empirical expression is: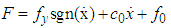 | (1) |
In the expressson, 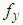 is Coulomb damping force, whose magnitude is related to the yield strength of MRF and the strength of external magnetic field;
is Coulomb damping force, whose magnitude is related to the yield strength of MRF and the strength of external magnetic field; 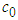 is the damping coefficient of magnetorheological fluids; it is the compensating force produced by the existence of accumulator.(2) Bouc-Wen ModelBouc-Wen’s model was first proposed by Bouc [5], which simulates hysteretic nonlinear systems through first-order differential equations. Then Wen modified the classical Bouc-Wen model on this basis [6]. This equations for Bouc-Wen’s model;
is the damping coefficient of magnetorheological fluids; it is the compensating force produced by the existence of accumulator.(2) Bouc-Wen ModelBouc-Wen’s model was first proposed by Bouc [5], which simulates hysteretic nonlinear systems through first-order differential equations. Then Wen modified the classical Bouc-Wen model on this basis [6]. This equations for Bouc-Wen’s model;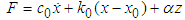 | (2) |
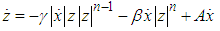 | (3) |
In the equation, 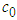 - viscous damping coefficient;
- viscous damping coefficient; 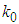 - stiffness coefficient; parameter
- stiffness coefficient; parameter 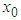 is the initial displacement; parameter
is the initial displacement; parameter 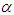 represents the ratio of pre-yielding to post-yeilding; parameter
represents the ratio of pre-yielding to post-yeilding; parameter 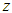 is a hysteretic displacement variable; parameters
is a hysteretic displacement variable; parameters 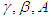 controls the linearity of unloading; parameter n is the coefficient of curve smoothness.
controls the linearity of unloading; parameter n is the coefficient of curve smoothness.
3. ACO and UKF Algorithms
(1) ACO Algorithm [7]The precedures of ACO algorithm are shown asŸ Estimate the scope of variables: 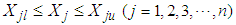 , in which
, in which 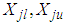 are the minmum and maxmun of
are the minmum and maxmun of 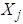 .Ÿ The scope of varibles is divided into N incremets, the dividing points with the value as
.Ÿ The scope of varibles is divided into N incremets, the dividing points with the value as 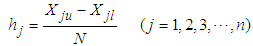 | (4) |
Ÿ The algorithm stops when 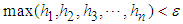 happens. The optimal solution is
happens. The optimal solution is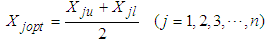 | (5) |
Ÿ The initial pheromones 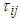 are same for every points when the iteration number
are same for every points when the iteration number 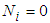 , and the amount of ants m, total pheromones Q, volatility coefficient
, and the amount of ants m, total pheromones Q, volatility coefficient 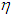 , maximum iteration Nmax are set. Ÿ Every ant selects next point according to the state transfer equation
, maximum iteration Nmax are set. Ÿ Every ant selects next point according to the state transfer equation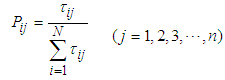 | (6) |
Ÿ The pheromone is modified in every loop based on the update equation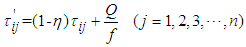 | (7) |
In which f is objective function value.Ÿ The iteration number is changed into Ni+1. If 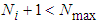 , go back to step 5; otherwise the the row
, go back to step 5; otherwise the the row 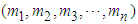 corresponding to the maxmum element in the column of
corresponding to the maxmum element in the column of 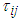 is searched in every interation and the scope of variables is decreased. The minmum and maxmun of the variales are
is searched in every interation and the scope of variables is decreased. The minmum and maxmun of the variales are 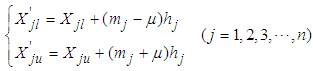 | (8) |
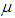 is in the range of [1,6]. Return to step 2.(2) UKF Algorithm [8]The discrete nonlinear system is described in the form:
is in the range of [1,6]. Return to step 2.(2) UKF Algorithm [8]The discrete nonlinear system is described in the form: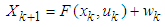 | (9) |
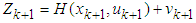 | (10) |
In which, 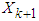 is the state vector at
is the state vector at 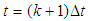 ,
, 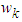 is the process noise vector of zero mean white noise Gaussian processes with covariance matrix
is the process noise vector of zero mean white noise Gaussian processes with covariance matrix 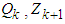 is the measurement vector at
is the measurement vector at 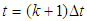 ,
, 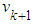 is the measurement noise vector of zero mean white noise Gaussian processes with covariance matrix
is the measurement noise vector of zero mean white noise Gaussian processes with covariance matrix 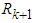 .At time step k, the (2n+1) sigma points are computed by
.At time step k, the (2n+1) sigma points are computed by 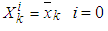 | (11-1) |
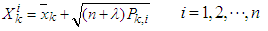 | (11-2) |
 | (11-3) |
In which: 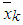 is the mean,
is the mean, 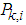 is the covariance while
is the covariance while 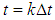 .the weights are
.the weights are 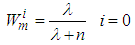 | (12-1) |
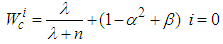 | (12-2) |
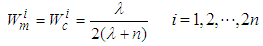 | (12-3) |
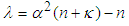 | (12-4) |
In which: n is the dimension of the state vector, 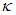 is a secondary scaling parameter which is usually set to 0 or (3-n),
is a secondary scaling parameter which is usually set to 0 or (3-n), 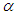 should be small positive number
should be small positive number 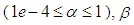 is a parameter,
is a parameter, 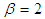 is the optimal for Gaussian distributions.The predicted state vector
is the optimal for Gaussian distributions.The predicted state vector 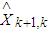 and its predicted covariance
and its predicted covariance 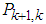 are computed as
are computed as 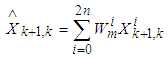 | (13) |
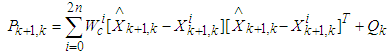 | (14) |
Similarly, the predicted measurement vector 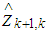 and predicted
and predicted 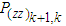 are calculated as
are calculated as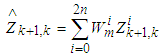 | (15) |
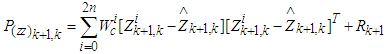 | (16) |
then the update step is as follows: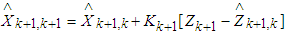 | (17) |
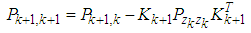 | (18) |
Where 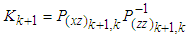 | (19) |
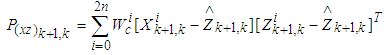 | (20) |
ACO algorithm is similar to most other intelligent algorithms. It has the potential to identify parameters in a wide range of their initial values, but the accuracy of the identified parametrs is not very high. The reason is that the algorithm mainly divides the range of parameter values into meshes and allow for ant colony selection by pheromones on the mesh points, so as to construct the shortest path, that is, the minimum value of the objective function. When the problem is complex, there may be multiple extreme points in the objective function. In addition, once the ant colony of grid partitioning falls into the local optimum stage, the grid will continue to partition in this part of the grid, so there is no way out of this dilemma. At the same time, the influence of parameters on the damping force is superimposed. When a large error occurs between one parameter and the true value, it will inevitably affect the other one or more parameters. At last, the characteristic curve of the model may coincide with the actual situation, but in the aspect of model parameters, there will be a large error [10].The accuracy of UKF algorithm is very high, but it depends very much on the accuracy of the initial value. The reason is that the untraceable change in UKF algorithm determines the sampling points around the original state. When the initial value is different from the real value, the sigma points collected are far away from the real value, which may easily lead to the divergence of UKF algorithm. Therefore, this paper combines the advantages of the two methods to identify the parameters of the Bingham model and the Bouc-Wen model of MR damper [11].
4. Parameter Identification of Bouc-Wen Model and Bingham Model
The identification is operated in the SIMULINK of MATLAB.The parameters of Bouc-Wen model and Bingham model in this paper are taken from reference [9]. The Bouc-Wen model is taken as an example for analysis and explanation. Firstly, the parameters are identified by ant colony optimization algorithm. For setting the initial range, the parameters are assumed to be in a larger range, such as formula (21) and (22).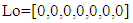 | (21) |
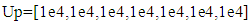 | (22) |
The “Lo” and “Up” sets define the lower and upper limits of the initial range respectively. The Bouc-Wen model in this range is identified several times, and the minimum values of each parameter identified in this round are taken as the minimum values in the next cycle, and the maximum values are taken as the maximum values in the next cycle. In the early stage of parameter identification, in order to shorten the optimization time, the number of ants was set to 50; whiles in the later stage, in order to improve the identification effect of parameters, the number of ants was gradually increased from 50 to 110. After 10 cycles, the idenfication range of Bouc-Wen model is limited to the range given in set (23) and set (24). At this time, the order of magnitude of the objective function value is reduced from the original 1E3 to 1E-4, which shows that the parameter range of the reduced range is closer to the real value.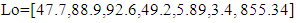 | (23) |
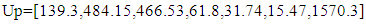 | (24) |
In order to reduce the errors caused by the randomness of parameter identification, this paper then identifies the parameters in this range, and draws the conclusion that the final result of parameter identification in this stage is as follows: 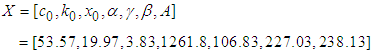 | (25) |
In the phase of UKF algorithm, the parameters of equation (25) are taken as initial values, and the Bouc-Wen model is identified for the second time. The process noise covariance is set to be 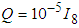 ; the observation covariance of the system is set to be
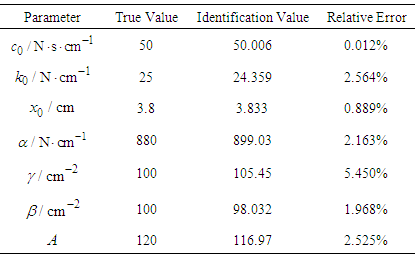
; the observation covariance of the system is set to be  ; the initial covariance is shown in set (26), The recognition process is shown in Figure 1, the relative error table is shown in Table 1, and the simulation results and experimental results of the characteristic curve are shown in Figure 2.
; the initial covariance is shown in set (26), The recognition process is shown in Figure 1, the relative error table is shown in Table 1, and the simulation results and experimental results of the characteristic curve are shown in Figure 2. 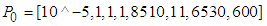 | (26) |
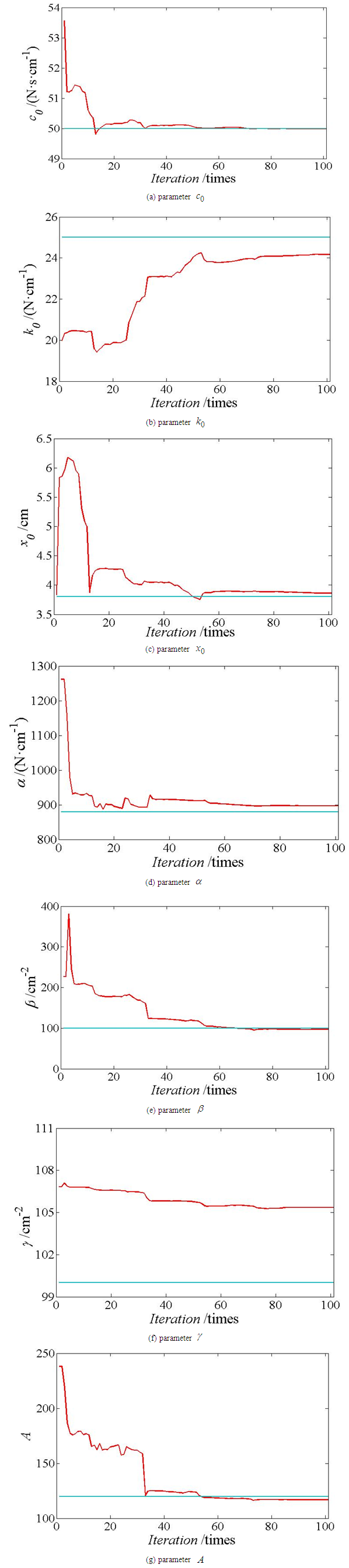 | Figure 1. Identification Process of Bouc-Wen |
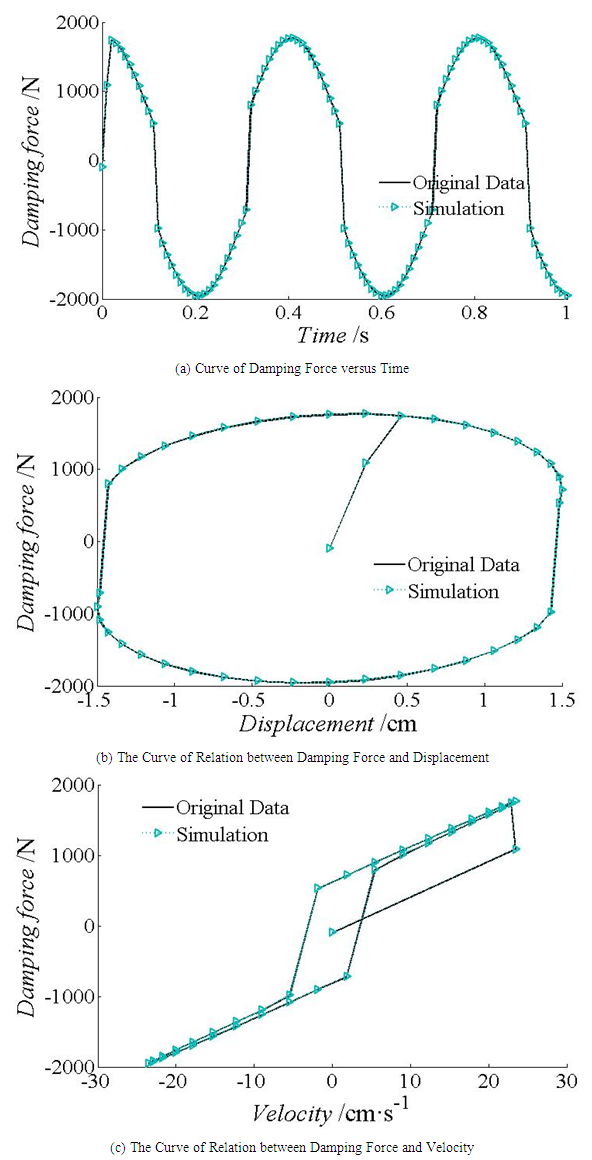 | Figure 2. Comparison of simulation results and experiments of Bouc-Wen model |
Following Figure 1, parameters 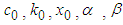 and A all reach convergence state and tend to true value after early identification fluctuation. And parameter
and A all reach convergence state and tend to true value after early identification fluctuation. And parameter 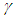 although it’s balanced in the later stage, the recognition value is far from the true value. Table 1 shows that the relative error of 5.45% of parameter
although it’s balanced in the later stage, the recognition value is far from the true value. Table 1 shows that the relative error of 5.45% of parameter 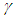 is the largest among other parameter. It can be considered that the identification process of the parameters in Fig. 1 (f) is acceptable. From Figure 2, the simulation results are in good agreement with the actual data. So the identification effect of this method is ideal.
is the largest among other parameter. It can be considered that the identification process of the parameters in Fig. 1 (f) is acceptable. From Figure 2, the simulation results are in good agreement with the actual data. So the identification effect of this method is ideal. Table 1. Relative Errors between Real Value and Idenfication Value of Bouc-Wen Model Parameters
 |
| |
|
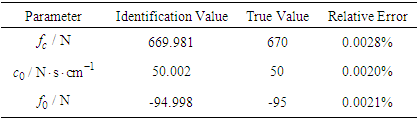
Similarly, the relative error of Bingham model identification is shown in Table 2, and the characteristic curve of the damper is shown in Figure 3. The solid line represents the behavior of MR with the known parameters which are obtained from reference [9], the dashed line represents the behavior of MR with the parameters identified by the combined method.It can be seen from Table 2 that the relative errors of the three parameters identified are very small, and their values are about 0.002%. In addition, Figure 3 shows that the simulation curve is in good agreement with the test curve. Therefore, the identification effect of the algorithm is very good in terms of parameter accuracy and coincidence.Table 2. Bingham’s Relative Errors between Model Recognition Value and Real Value
 |
| |
|
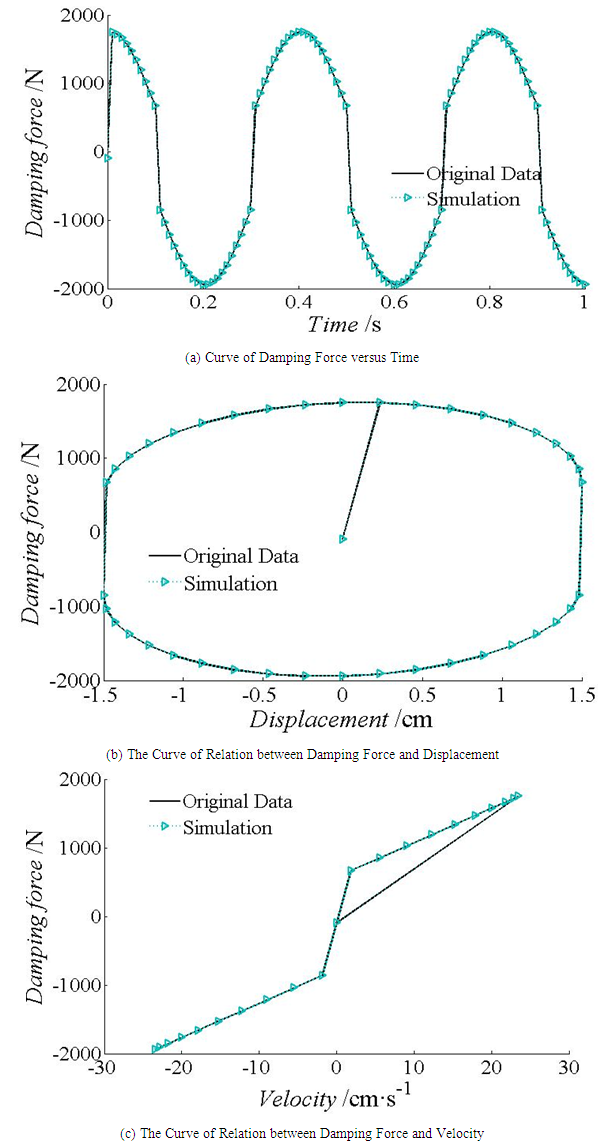 | Figure 3. Comparisons between simulation results and experimental results of Bingham model |
5. Conclusions
In this paper, an ACO algorithm is proposed to reduce the range of parameters to determine the initial value for UKF algorithm. Then, the unknown parameters in the model can be identified by utilizing the strong optimization ability of UKF algorithm. Through the analysis of two examples, it is found that this method is effective in identifying Bouc-Wen model and Bingham model parameters. It provides a reference for the identification of model parameters in practical application.
References
| [1] | Zhou Xiaohong, Liu Hongjun, Liu Peng. Magnetorheology Based on Genetic Algorithms Damper Model Parameter Identification [J]. Functional Materials, 2006, 6(37): 1016-1017. |
| [2] | Priya C.B, Gopalakrishnan N. Parameter identification of long stroke and short stroke MR damper for its use in semi-active vibration control[J]. Journal of the Institution of Engineering, 2016, 97(4): 405-414. |
| [3] | Phillips R W. Engineering applications of fluids with a variable yield stress [D]. California: University of California, Berkeley. |
| [4] | Stanway R, Sproston. Non-linear modeling of an electrorheological vibration damper[J]. Electrostatics, 1987, 20. |
| [5] | R Bouc. Forced vibration of mechanical systems with hysteresis[C]. Processing of the 4th International conference on nonlinear oscillation, Prague, Czechoslovakia, 1967. |
| [6] | Wen Y K. Method of random vibration of hysteretic system[J]. Journal of Engineering Mechanics Division, ASCE, 102, 1976. |
| [7] | Duan Haibin. Principle and Application of Ant Colony Algorithms [M]. Beijing: Science Press. 2005. |
| [8] | Julier S J, Uhlman J K, Durrant-Whyte H F. New approach for filtering nonlinear system[J]. Proceedings of the American Control Conference, 1995, 3:1628-1632. |
| [9] | Spencer B F, Dyke S J. Phenomenological model for magnetorheological dampers[J]. J for Eng Mech, 1997, 123(3): 230-238. |
| [10] | Xiao Zhirong, Zhang Zhengwei. Parameter identification of MR damper model based on ant colony optimization algorithm [J]. Journal of Zhejiang University of Science and Technology, 2018, 30 (1): 51-57. |
| [11] | Zhang Zhengwei. Study on parameter identification of MR damper mechanical model [D]. Zhejiang Institute of Science and Technology, 2018. |



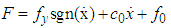
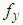 is Coulomb damping force, whose magnitude is related to the yield strength of MRF and the strength of external magnetic field;
is Coulomb damping force, whose magnitude is related to the yield strength of MRF and the strength of external magnetic field; 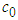 is the damping coefficient of magnetorheological fluids; it is the compensating force produced by the existence of accumulator.(2) Bouc-Wen ModelBouc-Wen’s model was first proposed by Bouc [5], which simulates hysteretic nonlinear systems through first-order differential equations. Then Wen modified the classical Bouc-Wen model on this basis [6]. This equations for Bouc-Wen’s model;
is the damping coefficient of magnetorheological fluids; it is the compensating force produced by the existence of accumulator.(2) Bouc-Wen ModelBouc-Wen’s model was first proposed by Bouc [5], which simulates hysteretic nonlinear systems through first-order differential equations. Then Wen modified the classical Bouc-Wen model on this basis [6]. This equations for Bouc-Wen’s model;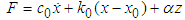
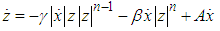
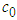 - viscous damping coefficient;
- viscous damping coefficient; 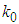 - stiffness coefficient; parameter
- stiffness coefficient; parameter 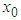 is the initial displacement; parameter
is the initial displacement; parameter 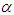 represents the ratio of pre-yielding to post-yeilding; parameter
represents the ratio of pre-yielding to post-yeilding; parameter 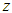 is a hysteretic displacement variable; parameters
is a hysteretic displacement variable; parameters 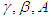 controls the linearity of unloading; parameter n is the coefficient of curve smoothness.
controls the linearity of unloading; parameter n is the coefficient of curve smoothness.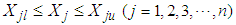 , in which
, in which 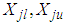 are the minmum and maxmun of
are the minmum and maxmun of 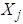 .Ÿ The scope of varibles is divided into N incremets, the dividing points with the value as
.Ÿ The scope of varibles is divided into N incremets, the dividing points with the value as 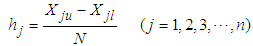
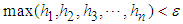 happens. The optimal solution is
happens. The optimal solution is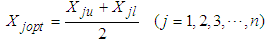
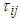 are same for every points when the iteration number
are same for every points when the iteration number 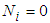 , and the amount of ants m, total pheromones Q, volatility coefficient
, and the amount of ants m, total pheromones Q, volatility coefficient 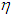 , maximum iteration Nmax are set. Ÿ Every ant selects next point according to the state transfer equation
, maximum iteration Nmax are set. Ÿ Every ant selects next point according to the state transfer equation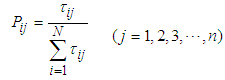
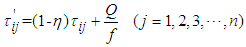
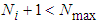 , go back to step 5; otherwise the the row
, go back to step 5; otherwise the the row 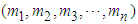 corresponding to the maxmum element in the column of
corresponding to the maxmum element in the column of 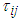 is searched in every interation and the scope of variables is decreased. The minmum and maxmun of the variales are
is searched in every interation and the scope of variables is decreased. The minmum and maxmun of the variales are 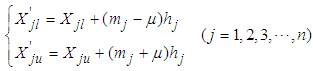
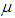 is in the range of [1,6]. Return to step 2.(2) UKF Algorithm [8]The discrete nonlinear system is described in the form:
is in the range of [1,6]. Return to step 2.(2) UKF Algorithm [8]The discrete nonlinear system is described in the form: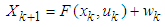
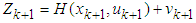
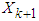 is the state vector at
is the state vector at 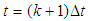 ,
, 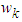 is the process noise vector of zero mean white noise Gaussian processes with covariance matrix
is the process noise vector of zero mean white noise Gaussian processes with covariance matrix 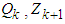 is the measurement vector at
is the measurement vector at 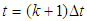 ,
, 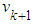 is the measurement noise vector of zero mean white noise Gaussian processes with covariance matrix
is the measurement noise vector of zero mean white noise Gaussian processes with covariance matrix 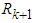 .At time step k, the (2n+1) sigma points are computed by
.At time step k, the (2n+1) sigma points are computed by 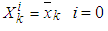
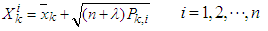

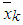 is the mean,
is the mean, 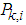 is the covariance while
is the covariance while 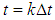 .the weights are
.the weights are 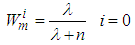
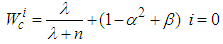
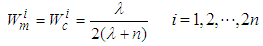
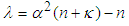
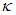 is a secondary scaling parameter which is usually set to 0 or (3-n),
is a secondary scaling parameter which is usually set to 0 or (3-n), 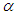 should be small positive number
should be small positive number 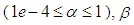 is a parameter,
is a parameter, 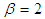 is the optimal for Gaussian distributions.The predicted state vector
is the optimal for Gaussian distributions.The predicted state vector 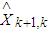 and its predicted covariance
and its predicted covariance 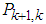 are computed as
are computed as 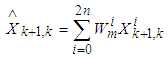
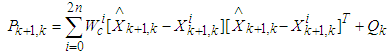
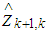 and predicted
and predicted 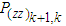 are calculated as
are calculated as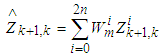
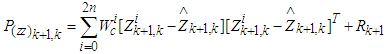
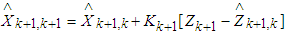
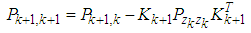
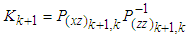
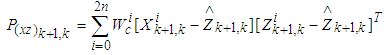
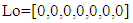
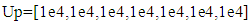
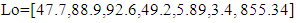
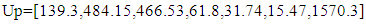
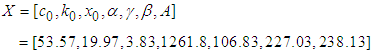
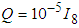 ; the observation covariance of the system is set to be
; the observation covariance of the system is set to be 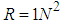 ; the initial covariance is shown in set (26), The recognition process is shown in Figure 1, the relative error table is shown in Table 1, and the simulation results and experimental results of the characteristic curve are shown in Figure 2.
; the initial covariance is shown in set (26), The recognition process is shown in Figure 1, the relative error table is shown in Table 1, and the simulation results and experimental results of the characteristic curve are shown in Figure 2. 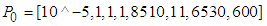


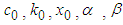 and A all reach convergence state and tend to true value after early identification fluctuation. And parameter
and A all reach convergence state and tend to true value after early identification fluctuation. And parameter 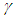 although it’s balanced in the later stage, the recognition value is far from the true value. Table 1 shows that the relative error of 5.45% of parameter
although it’s balanced in the later stage, the recognition value is far from the true value. Table 1 shows that the relative error of 5.45% of parameter 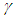 is the largest among other parameter. It can be considered that the identification process of the parameters in Fig. 1 (f) is acceptable. From Figure 2, the simulation results are in good agreement with the actual data. So the identification effect of this method is ideal.
is the largest among other parameter. It can be considered that the identification process of the parameters in Fig. 1 (f) is acceptable. From Figure 2, the simulation results are in good agreement with the actual data. So the identification effect of this method is ideal. 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
