-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2017; 7(4): 120-123
doi:10.5923/j.jce.20170704.02

Theoretical Discussion of a Model of Permeability Based on Soil Particle Diameters
Iván A. Patiño-Ramírez, Omar Chávez-Alegría
Autonomous University of Queretaro, Queretaro, Mexico
Correspondence to: Iván A. Patiño-Ramírez, Autonomous University of Queretaro, Queretaro, Mexico.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The permeability is a parameter widely studied by many researchers in area of soil mechanics. Its application to land routes is very important around the world, due to the interaction between the geomechanical behaviour and the change in the soil moisture, because of time variability in dry or wet conditions. The hydraulic conductivity or permeability of a soil is the speed at which a fluid is able to pass through the solid particles under a unit hydraulic gradient and once known, this property is an important parameter for the design of filter layers or for the development and implementation of drainage in the civil infrastructure. The hydraulic conductivity is generally measured by laboratory tests using soil samples with standardized methods or in field with specialized devices. Several authors have attempted to obtain mathematical models that are able to determine soil permeability. In order to obtain this permeability parameter, particle size distribution is include in the analysis. This paper compares a mathematical model published recently in literature, with results associated with these parameters obtained by many researchers around the world on basis of independent lab testing, of the model in question. Relations are established between particle size of the material and permeability coefficient. The analysis presented herein indicates that is necessary incorporation of other variables that affect permeability coefficient of soils, such as energy of compaction or void ratio, both are necessary to get a more accurate model and applicable to the solution of problems in soil mechanics.
Keywords: Hydraulic conductivity, Mathematical model, Permeability, Permeability coefficient, Particle diameter, Particle size distribution
Cite this paper: Iván A. Patiño-Ramírez, Omar Chávez-Alegría, Theoretical Discussion of a Model of Permeability Based on Soil Particle Diameters, Journal of Civil Engineering Research, Vol. 7 No. 4, 2017, pp. 120-123. doi: 10.5923/j.jce.20170704.02.
Article Outline
1. Introduction
- The roads are stratified materials with many characteristics and qualities, in general [1] mentions that, materials with better quality are at the top of the pavement structure, this is due to the fact that layers are built to absorb dynamic loads that generates stress primarily on pavement surface. Additionally, it is essential to know that hydraulic properties of those, as the permeability, susceptibility to moisture change and suction that present. As these will determine their correct behaviour as a material for the layers of the pavement to provide a safe and stable structure for expected useful life.It is well known that, change in water content in the soil matrix has an important effect on the mechanical properties of the layers of the pavement [2]. This variation is produced by excess water in the layers, which must be conducted outside of the structure, since this fluid can cause reduction in rigidity of the embankment and this loss is considered an important factor in pavement design; these is supported by authors such as [3-5] and more recently by [6], if water is not removed quickly, the layers will get saturated [7-9]. In addition to foregoing [10] said that, in practice, the effect of water content is implicitly considered through the elastic modulus.According to that some authors [11] have two strategies for the design of layers concerning to humidity control. The first one is to prevent water infiltration, and the second is rapid removal of water that infiltrates in pavement structure. The above is supported by [12], however with three controls [11], approaches to control or reduce problems caused by the change in water content. The first one is, to prevent moisture from within the pavement, the second is to use materials that are insensitive to effects when moisture changes, and the third is rapid removal of water infiltration into pavement.The pavements must have layers of granular material with adequate drainage for water removal, authors such as [13, 14] mentioned importance in mechanical understanding of materials used on roads, in order to provide an efficient drainage to eject water out of the structure as soon as possible, which is essential for proper long-term performance of the pavement. The layers that should be designed to provide drainage for both rigid and flexible pavements is the hydraulic base and sub-base, so that mechanical behaviour of this is preserved as uniform and high as possible [8, 15, 16] mentioned that to give an adequate water flow from pavement base by the use of a graduation open is effective; however [17] mention that the use of this type of graduation could lead to reduced stability and rigidity.As described above, it is important to generate adequate drainage to avoid problems in the pavement structure during its useful life. Water flow in a soil is attributed to the permeability coefficient and authors [13, 14, 18-20], have attempted to obtain mathematical models for determination of this coefficient to have a better understanding of soil mechanics used in the roads construction. So in this document, a model developed by [21] is evaluated according to a data base achieved from three investigations. On the other hand, stability and security of hydraulic structures are important qualities for hydraulic bases and filter layers designers in general; porous medium being the one that offers water removal at the beginning of its service life, performance can be significantly reduced through the incorporation of material, affecting in this way the structure and the life span [20].
2. Saturated Permeability Coefficient, Ks
- After years of failing attempting to seal the layers of the pavement structure, professionals of the area cannot prevent water infiltration to layers of the pavement. So, water removal is going to be fundamental for pavement, to have a better behaviour according to [11, 12]. Water infiltration can enter by multiple zones on the pavement structure, in Figure 1 shows ways of water movement in the structure of the embankment.
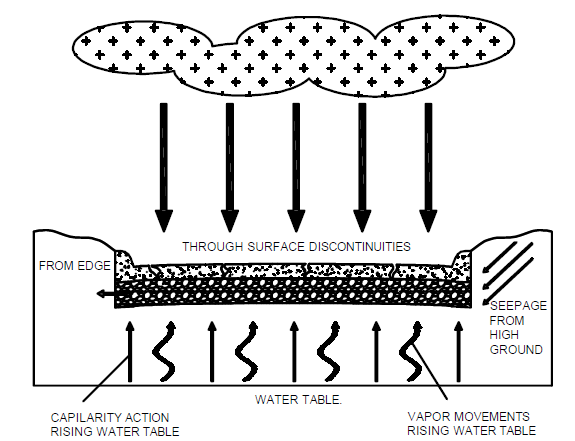 | Figure 1. How pavement gets saturated |
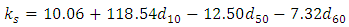 | (1) |
3. Samples to Compare
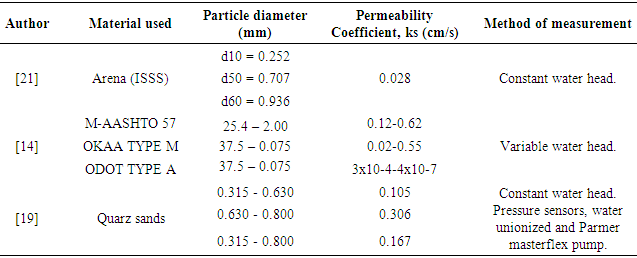
- As a result of investigations in geotechnics, authors such as [13, 14, 18-20], have joined in the description of mathematical models for the determination of a soil permeability coefficient. Product of the above mentioned, countless assay of conductivity has been made to many types of soils with different methods, but all with the same purpose, to predict hydraulic flow through a mass of soil. Table 1 shows some authors that have been reviewed, for seeking and obtaining the values of permeability coefficients, as well as characteristics of the soil tested by them and those of [21].
|
4. Results
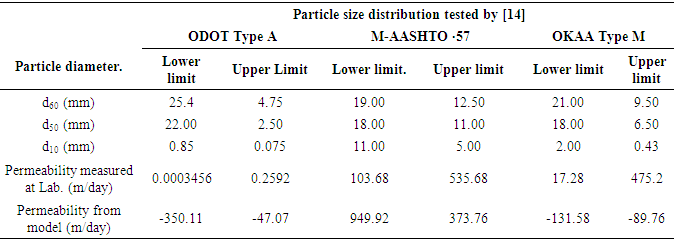
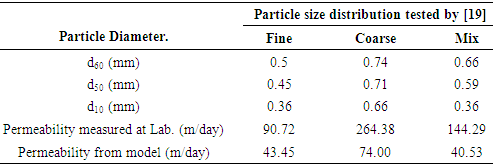
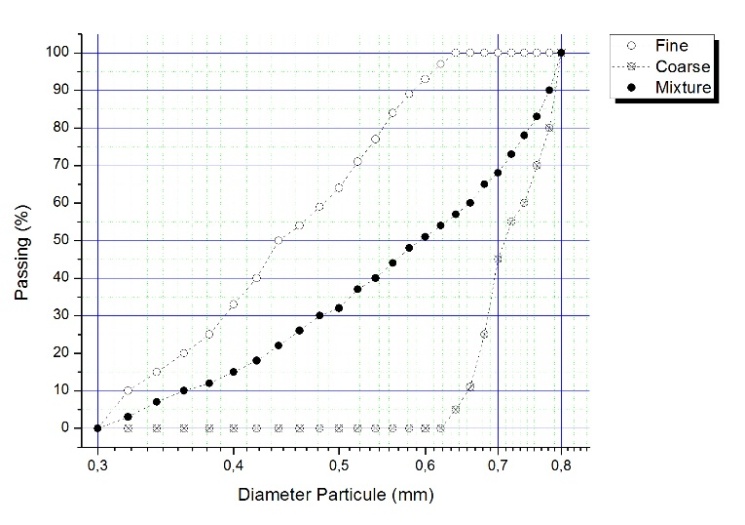
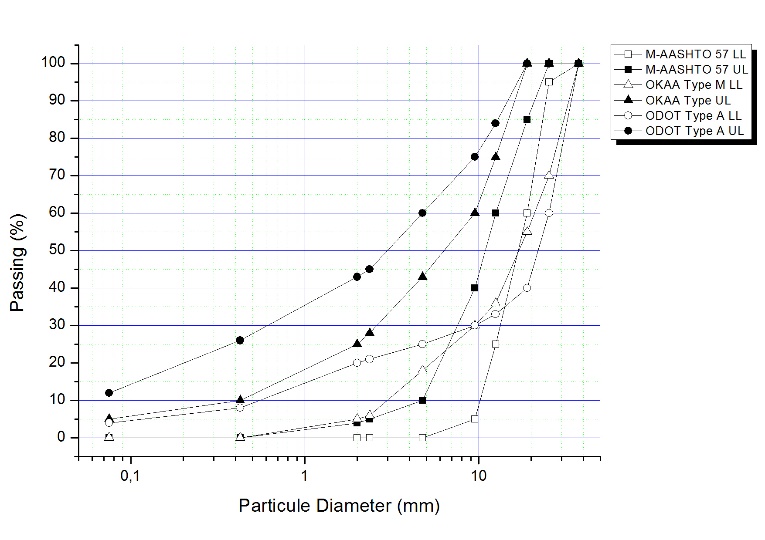
- The application of equation 1 was made according to parameters provided by the authors [14] and [19]. For its part [14], provided in their research article grain size distribution from soil classifications ODOT Type A, M-AASHTO number 57 and OKAA Type M; the three grain sizes were evaluated in the lower and the upper limits, which are presented in Figure 2. On the other hand, [19] provide only minimum and maximum parameters in terms of sizes of aggregates together with coefficients of uniformity (Cu) for the three proposals that studies which referred to as fine, coarse and a mixture of both, with which they can propose grain sizes that are conform to the same which are presented in Figure 3.
 | Figure 2. Particle size distribution [14] |
 | Figure 3. Particle size distribution [19] |
|
|
5. Conclusions
- As can be seen there are no correlation between values obtained with the model presented by [21] and its grain size distribution itself. For this reason, it is concluded that more research is needed to find a correct mathematical model, which could be incorporated into the analysis of other variables for prediction of ‘ks’ such as energy of compaction or void ratio. The model proposed by [21] had a great approximation in the determination of permeability coefficient for materials used in its research; however, as shown in tables 2 and 3, when applied to other materials this is not consistent.More research is required to needed cover materials from different backgrounds, as well as various tests are necessary, in addition to incorporation of more variables, in order to develop a model that is applicable to soils with heterogeneous characteristics or failing to establish boundary conditions for the implementation of multiple models.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML