Hongyan Shi, Aobo Zhang
School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou, China
Correspondence to: Hongyan Shi, School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou, China.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Based on the condition of equal vertical strain, a general solution for the degree of consolidation of soils by vertical drains under both arbitrary surcharge and vacuum preloading, including instantaneous preloading, is proposed, which can take into account the well resistance and the smear effect, radial and vertical direction permeability. Furthermore, an analytical solution for the degree of consolidation under linear time-dependent loading is also presented. The feasibility of the solution is proved by 3-D finite element method. The solution shows that Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain.
Keywords:
Soils by vertical drains, Arbitrary surcharge and vacuum preloading, Degree of consolidation, Analytical solution
Cite this paper: Hongyan Shi, Aobo Zhang, Degree of Consolidation of Soils by Vertical Drains under Arbitrary Surcharge and Vacuum Preloading, Journal of Civil Engineering Research, Vol. 7 No. 2, 2017, pp. 72-80. doi: 10.5923/j.jce.20170702.07.
1. Introduction
The vertical drains, in combination with surcharge or/and vacuum preloading, is a good method to improve saturated soft soils. It is necessary to evaluate the consolidation degree of soil for selecting the proper loading rate and estimating its strength change as well as avoiding its shear failure during loading. There are two types of consolidation theory for soils by vertical drains. One is called the equal vertical strain [1, 2], another is called the free strain [3, 4]. The former is perfect in theory but very complicated because of its implicit form. The latter is not perfect in theory but has a simple form. The research results prove that there is only the slight difference for consolidation degree between the equal vertical strain and the free strain [4]. Therefore, the latter is widely applied to analyze the consolidation of soils by vertical drains. The different solutions for consolidation degree of the soils are given according to the different conditions of preloading (surcharge or/and vacuum preloading, instantaneous or/and time–dependent loading), smear effect (whether considering smear effect or not) and permeability (whether considering vertical flow of soils or not) [4-7]. So far, there is not a general solution including the above-mentioned different conditions yet.Based on the condition of the equal vertical strain, a solution for the degree of consolidation of soils by vertical drains under arbitrary surcharge and vacuum preloading (including instantaneous preloading) is proposed taking into account the well resistance and the smear effect, radial and vertical direction permeability, and an analytical solution for consolidation degree under linear time-dependent loading is also presented. The feasibility of the solutions are proved by 3-D finite element method.
2. Analysis Model and Its Basic Assumptions
The analysis model, a soil cylinder having a vertical drain, is schematically pictured in Fig.1. In the figure, H is the length of drain, Rw, Rs and Re are the radii of drain, smeared zone and influence zone of drain respectively, kw is the coefficient of permeability of drain, ks and kh are the radial coefficients of permeability of smeared zone and undisturbed zone respectively, kv is the vertical coefficient of permeability of smeared zone and undisturbed zone, r and z are the radial and vertical coordinates respectively.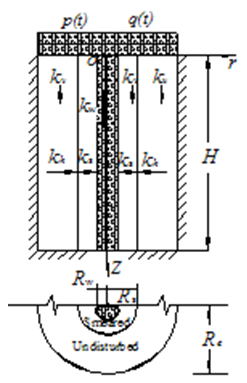 | Figure 1. Schematic picture of soil cylinder with vertical drain |
2.1. Basic Assumptions
The basic assumptions in this study are listed as follows:(1) Barron’s hypothesis of the equal vertical strain is valid. Lateral deformation of soil is ignored, and vertical strain is same at the same depth.(2) Radial flow in drain is neglected, and the total inflow of the pore water through the boundary of the vertical drain is equal to the vertical flow of the pore water within the vertical drain.(3) Darcy’s law is valid.(4) The bottom of soil is impervious.(5) The vacuum and surcharge preloadings are schematically pictured in Fig.2. In the figure, p(t) and q(t) denote for vacuum and surcharge preloading respectively, p(0) and q(0) are vacuum and surcharge preloadings at time t=0 respectively, pu and qu are ultimate vacuum and surcharge preloadings respectively.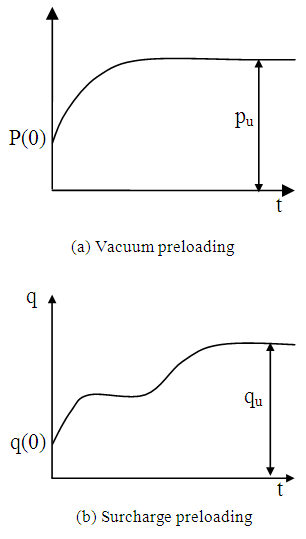 | Figure 2. Schematic picture of vacuum and surcharge preloading |
2.2. Basic Partial Differential Equations of Analysis Model and Their Solutions
Let 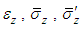 and
and 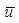 denote for the average strain, average total stress, average effective stress and average excess pore water pressure at the depth z, respectively, and mv is the coefficient of volume compressibility of soil. According to the above assumptions, the following equations can be got,
denote for the average strain, average total stress, average effective stress and average excess pore water pressure at the depth z, respectively, and mv is the coefficient of volume compressibility of soil. According to the above assumptions, the following equations can be got,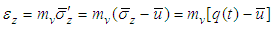 | (1) |
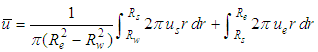 | (2) |
where 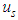 and
and 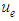 are the excess pore water pressure within the smeared zone and the undisturbed zone respectively. Taking Derivative of Eq.(1) with respect to t, the following equation is obtained,
are the excess pore water pressure within the smeared zone and the undisturbed zone respectively. Taking Derivative of Eq.(1) with respect to t, the following equation is obtained,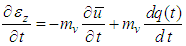 | (3) |
In addition, 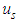 and
and 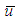 should satisfy the following equations:
should satisfy the following equations: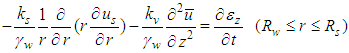 | (4) |
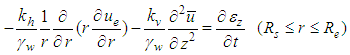 | (5) |
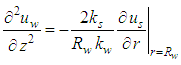 | (6) |
where 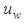 is the pore pressure in the drain,
is the pore pressure in the drain, 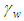 is the unit weight of water. The solution conditions for the above Eqs. (1)~(6) are expressed asBoundary conditions:(1)
is the unit weight of water. The solution conditions for the above Eqs. (1)~(6) are expressed asBoundary conditions:(1) 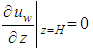 (The bottom of drain is impervious)(2)
(The bottom of drain is impervious)(2) 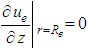 (The cylindrical surface of soil is impermeable)(3)
(The cylindrical surface of soil is impermeable)(3) 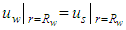 (Continuity of pore water pressure at
(Continuity of pore water pressure at 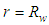 )(4)
)(4) 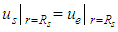 (Continuity of pore water pressure at
(Continuity of pore water pressure at 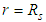 )(5)
)(5) 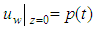 (Pore water pressure at the top of drain is equal to the vacuum preloading)Initial conditions:(1)
(Pore water pressure at the top of drain is equal to the vacuum preloading)Initial conditions:(1) 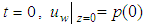 (2)
(2) 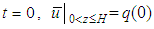 Integrating of Eqs.(4) and (5) with the boundary conditions (2), (3) and (4),
Integrating of Eqs.(4) and (5) with the boundary conditions (2), (3) and (4),  and
and  can be obtained as follows.
can be obtained as follows.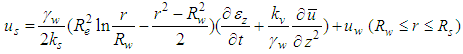 | (7) |
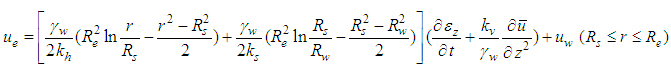 | (8) |
Substituting Eqs. (7) and (8) into Eq.(2), the average pore water pressure 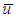 is presented,
is presented,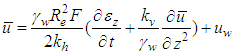 | (9) |
here, 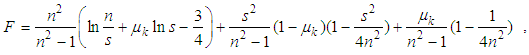
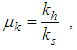
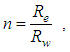
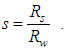 Substituting Eq. (7) into Eq.(6), the following expression can be obtained,
Substituting Eq. (7) into Eq.(6), the following expression can be obtained,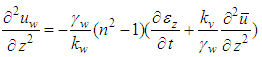 | (10) |
Combining with Eq.(9) and Eq.(3), and eliminating 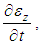 the following equation is got,
the following equation is got,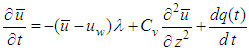 | (11) |
where  and
and 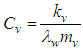 are the radial and coefficients of permeability of soil respectively. Combining with Eq.(9) and Eq.(10), and eliminating
are the radial and coefficients of permeability of soil respectively. Combining with Eq.(9) and Eq.(10), and eliminating 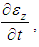 the following equation is obtained,
the following equation is obtained,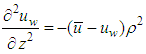 | (12) |
where 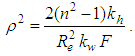 Combining with Eq.(11) and Eq.(12), and eliminating
Combining with Eq.(11) and Eq.(12), and eliminating 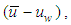 the following equation is got,
the following equation is got,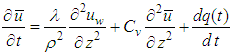 | (13) |
Combining with Eq.(12) and Eq.(13),and eliminating 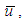 the equation about
the equation about 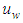 can be expressed as
can be expressed as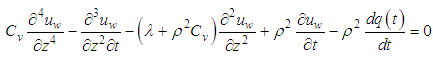 | (14) |
In order to solve inhomogeneous Eq.(14), the following transformation is applied: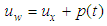 | (15) |
where 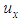 is called the transformed variable,
is called the transformed variable, 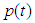 is vacuum preloading. Substituting Eq.(15) into Eq.(14), it can be rewritten as
is vacuum preloading. Substituting Eq.(15) into Eq.(14), it can be rewritten as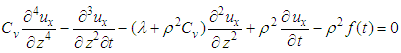 | (16) |
in which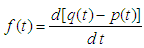 | (17) |
At the same time, the boundary conditions (1) and (5) can be rewritten as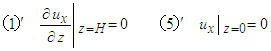 Using the separation of variables, and using the boundary conditions
Using the separation of variables, and using the boundary conditions 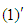 and
and 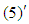 , the solution for Eq.(16) is
, the solution for Eq.(16) is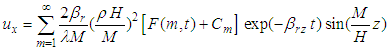 | (18) |
where 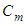 is an undetermined coefficient,
is an undetermined coefficient, 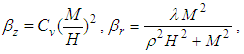
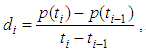
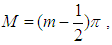
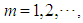 and
and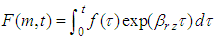 | (19) |
Here, 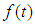 is expressed as Eq.(17). Substituting Eq. (18) into Eq.(15), the solution for
is expressed as Eq.(17). Substituting Eq. (18) into Eq.(15), the solution for 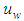 is
is 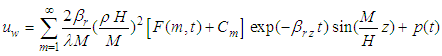 | (20) |
Substituting Eq. (20) into Eq.(12) and using the initial condition (1) and (2), the solution for 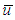 is
is 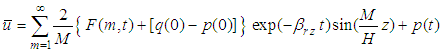 | (21) |
The vertical displacement at the top of soil, 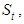 can be determined as follows.
can be determined as follows.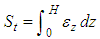 | (22) |
Using Eqs.(1), (21) and (22), 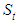 is expressed as
is expressed as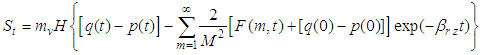 | (23) |
When 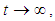 the ultimate vertical displacement at the top of soil,
the ultimate vertical displacement at the top of soil, 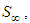 can be got from Eq.(23) as
can be got from Eq.(23) as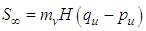 | (24) |
where pu and qu are the ultimate vacuum and surcharge preloadings respectively (see Fig.2). The overall average degree of consolidation for the whole soil, 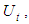 is defined as follows.
is defined as follows.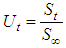 | (25) |
Substituting Eqs. (23) and (24) into Eq.(25), 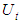 can be expressed as
can be expressed as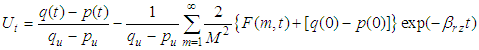 | (26) |
where 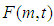 is expressed as Eq.(19).
is expressed as Eq.(19).
3. The Degree of Consolidation for Soil under Linear Multi-Loading
In practice, preloading is exerted step-by-step, and the loading per step can be seen approximately linear (as shown in Fig.3). Let n denote for the total step numbers of loading, for the i-th step 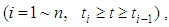 the vacuum preloading p(t) and surcharge preloading q(t) can be expressed as
the vacuum preloading p(t) and surcharge preloading q(t) can be expressed as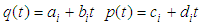 | (27) |
where 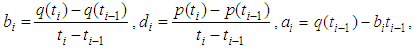
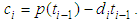 If
If 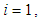 then
then 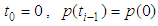 ,
,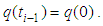 Note that when
Note that when 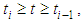 Eq.(19) can be expressed as
Eq.(19) can be expressed as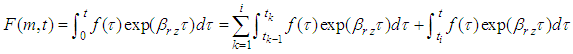 Substituting Eq.(27) into the above equation,
Substituting Eq.(27) into the above equation, 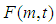 can be rewritten as
can be rewritten as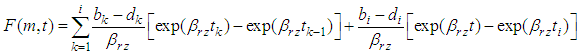 Substituting the above equation into Eq.(26), the average degree of consolidation
Substituting the above equation into Eq.(26), the average degree of consolidation  for linear multi-loading can be expressed as
for linear multi-loading can be expressed as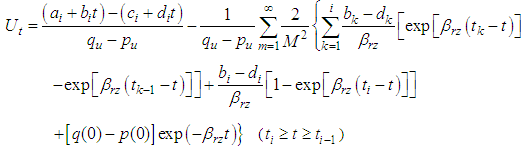 | (28) |
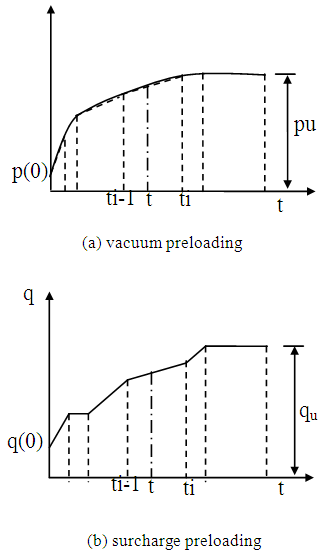 | Figure 3. Schematic picture for linearized vacuum and surcharge preloadings |
4. Discussion
4.1. Relation between Preloading with Degree of Consolidation
From Eq.(28), it is easily seen that the degree of consolidation for soil is dependent on the totality of surcharge and vacuum loading rather than their respective proportion. Especially, if surcharge loading is equal to vacuum loading, that is q(t)=-p(t), they have the same degree consolidation. Obviously, It is right that to convert the vacuum loading into the equivalent amount of surcharge when calculating the degree of consolidation.Under instantaneous loading, 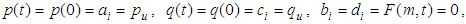 Eq.(28) becomes
Eq.(28) becomes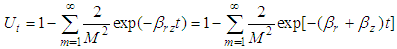 | (29) |
The above equation shows that the degree of consolidation under instantaneous loading is independent of the type of preloading.Additionally, if the vertical flow is ignored, that is 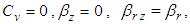 Eq.(29) is identical to Dong Zhi-liang’s formulation [5].If the radial flow is ignored, that is
Eq.(29) is identical to Dong Zhi-liang’s formulation [5].If the radial flow is ignored, that is 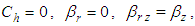 Eq.(29) degenerates into
Eq.(29) degenerates into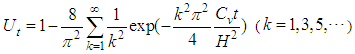 | (30) |
which is identical to Terzaghi’s formulation for one-dimensional consolidation.
4.2. The Degree of Consolidation under Vacuum Preloading
If vacuum loading is only considered, that is 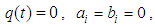 Eq.(28) degenerates into
Eq.(28) degenerates into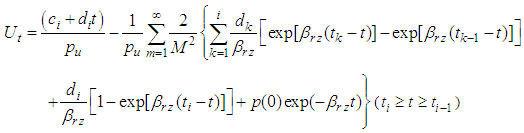 | (31) |
Further, if vertical flow is neglected, Eq.(31) is identical to Yin Jing’s formulation [6].
4.3. The Degree of Consolidation under Surcharge Preloading
If surcharge loading is only considered, that is 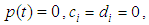 Eq.(28) degenerates into
Eq.(28) degenerates into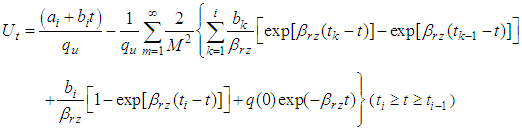 | (32) |
which is identical to Xiao-Wu Tang’s formulation [7].Especially, if loading is instantaneous, that is 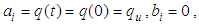 Eq.(32) is same as to Eq.(29). Besides, if vertical flow is ignored, that is
Eq.(32) is same as to Eq.(29). Besides, if vertical flow is ignored, that is 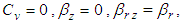 Eq.(32) becomes
Eq.(32) becomes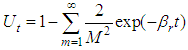 | (33) |
which is identical to Xie Kang-he’s formula [4].
4.4. The Feasibility of Carrilo’s Method Used to Calculate the Degree of Consolidation
When both radial and vertical flow are considered, the overall average degree of consolidation of soils, 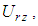 can be determined according to Carrilo’s method.
can be determined according to Carrilo’s method.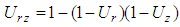 Where
Where 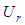 and
and 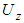 are the overall degree of consolidation for radial and vertical flow respectively. It is usually considered that Carrilo’s method is valid under time-independent loading (i.e., instantaneous loading). Under this condition, let
are the overall degree of consolidation for radial and vertical flow respectively. It is usually considered that Carrilo’s method is valid under time-independent loading (i.e., instantaneous loading). Under this condition, let 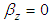 and
and 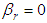 in Eq.(29) respectively,
in Eq.(29) respectively, 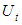 in the equation denotes for the degree of consolidation without vertical and without vertical flow
in the equation denotes for the degree of consolidation without vertical and without vertical flow 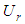 and
and 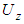 respectively. Obviously
respectively. Obviously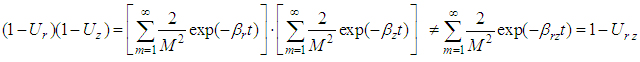 It is concluded that Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain because the average pore pressure
It is concluded that Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain because the average pore pressure 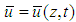 is adopted in Eqs.(4) and (5) according to the assumption of equal vertical strain.
is adopted in Eqs.(4) and (5) according to the assumption of equal vertical strain.
5. Validation of the Solution Used 3-D Finite Element Method
Here the 3-D FEM is applied to verify Eq.(26). The FEM equations for consolidation take the form of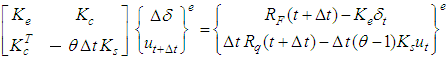 | (34) |
Here, 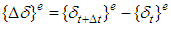 is the increments of nodal displacements in a element,
is the increments of nodal displacements in a element, 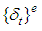 and
and 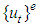 are the nodal displacements and nodal pore pressures at respectively,
are the nodal displacements and nodal pore pressures at respectively, 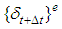 and
and 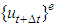 are the nodal displacements and pore pressures at
are the nodal displacements and pore pressures at 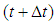 respectively,
respectively, 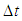 is time interval,
is time interval, 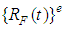 is nodal forces at t,
is nodal forces at t, 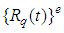 is nodal discharge matrix at t, and usually is zero [8].
is nodal discharge matrix at t, and usually is zero [8]. 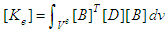 ,
, 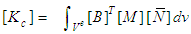 and
and 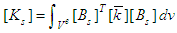 are the element stiffness matrix, element coupled matrix and element seepage matrix respectively,
are the element stiffness matrix, element coupled matrix and element seepage matrix respectively, 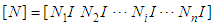 and
and  are the shape function matrixes for displacement and pore pressure respectively, I is a
are the shape function matrixes for displacement and pore pressure respectively, I is a 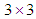 unit matrix,
unit matrix, 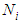 and
and 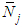 are the shape functions for displacement and pore pressure respectively, n and m are the total nodal numbers of displacement and pore pressure in a element respectively, {M}={1 1 1 0 0 0}T,
are the shape functions for displacement and pore pressure respectively, n and m are the total nodal numbers of displacement and pore pressure in a element respectively, {M}={1 1 1 0 0 0}T, 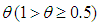 is an integral constant, and usually 0.5 or 2/3,
is an integral constant, and usually 0.5 or 2/3,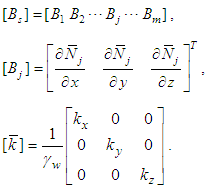 The assumed data for the verification are: Rw=5cm, Rs=2Rw, Re=20Rw, kw=2
The assumed data for the verification are: Rw=5cm, Rs=2Rw, Re=20Rw, kw=2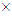 10-2cm/s, ks= 6
10-2cm/s, ks= 6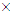 10-8cm/s, kh=kv=ks; mv=5
10-8cm/s, kh=kv=ks; mv=5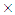 10-4kPa-1, elastic modulus E=1246.15kPa and Poisson’s ratio μ=0.35.The one-eighth of soil is considered because of its symmetry. The soil is vertically divided into some layers, and the elements in a layer are shown in Fig.4. The length of the drain, H=10m, is considered, and three cases: (1) vacuum loading only, (2) surcharge loading only and (3) combined vacuum and surcharge loading, are analyzed. Pentahedron element with 15 displacement nodes and 6 pore pressure nodes for the drain, and hexahedron element with 20 displacement nodes and 8 pore pressure nodes for the smeared zone and undisturbed zone, are used for the analysis.
10-4kPa-1, elastic modulus E=1246.15kPa and Poisson’s ratio μ=0.35.The one-eighth of soil is considered because of its symmetry. The soil is vertically divided into some layers, and the elements in a layer are shown in Fig.4. The length of the drain, H=10m, is considered, and three cases: (1) vacuum loading only, (2) surcharge loading only and (3) combined vacuum and surcharge loading, are analyzed. Pentahedron element with 15 displacement nodes and 6 pore pressure nodes for the drain, and hexahedron element with 20 displacement nodes and 8 pore pressure nodes for the smeared zone and undisturbed zone, are used for the analysis.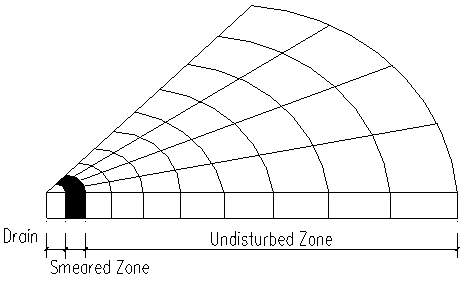 | Figure 4. Schematic picture of a layer element mesh of soil |
The degree of consolidation for soil is calculated according to Eq.(25). It is notable that St in Eq.(25) is the average vertical displacement at the top of soil,which is got by FEM.
5.1. For Instantaneous Loading
For the exerted loadings 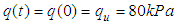 and
and 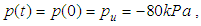 the comparisons between the calculated degree of consolidation by the FEM and got one from Eq.(26) are shown in Fig.5. It is clearly evident that both are in good agreement.
the comparisons between the calculated degree of consolidation by the FEM and got one from Eq.(26) are shown in Fig.5. It is clearly evident that both are in good agreement.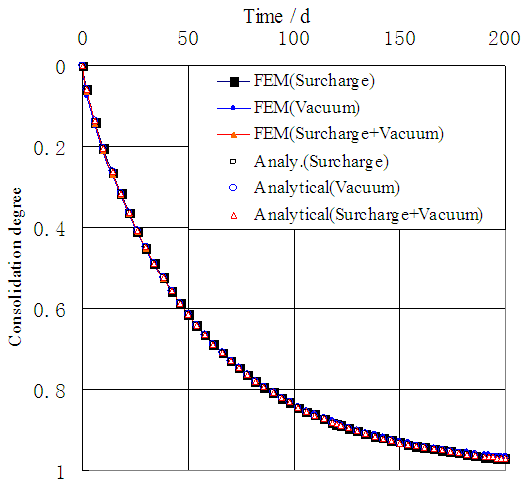 | Figure 5. Comparison between the calculated consolidation degree by FEM and got one by analytical solution |
5.2. For Multi-Loading
The assumed vacuum and surcharge loadings are shown in Fig.6. The comparisons between the calculated degree of consolidation by FEM and got one from Eq.(26) is shown in Fig.7. It is obvious that both are also good consistent.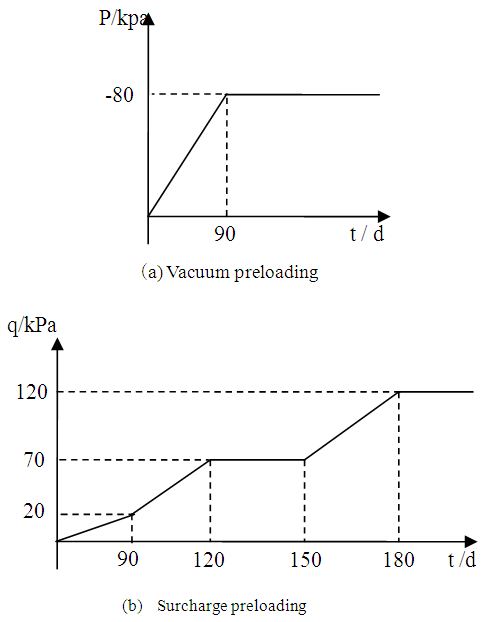 | Figure 6. Assumed vacuum and surcharge preloading |
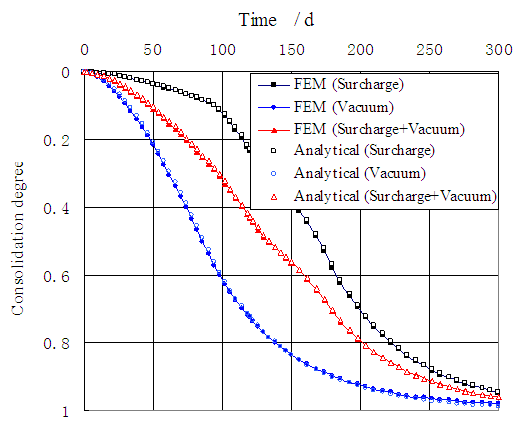 | Figure 7. Comparison between the calculated consolidation degree by FEM and got one by analytical solution |
6. Conclusions
(1) The solution for the degree of consolidation of soils by vertical drains under both arbitrary surcharge and vacuum preloading, including instantaneous preloading, is proposed taking into account the well resistance and the smear effect, radial and vertical direction flow, and an analytical solution for the degree of consolidation under linear time-dependent loading is also presented.(2) The degree of consolidation for soil is dependent on the totality of surcharge and vacuum loading rather than their respective proportion. It is right that to convert the vacuum loading into the equivalent amount of surcharge when calculating the degree of consolidation.(3) Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain.
References
| [1] | Barron R.A., Consolidation of Fine Grained soils by drained wells[J], Trans., ASCE, 1948, 113: 718-733. |
| [2] | Yoshikumi, H, Nakanodo, H,, Consolidation of Soils by Vertical Drain Wells with Finite Permeability[J], Soils and Foundations, 1974, 34(2): 35-46. |
| [3] | Hansbo, S., Consolidation of Fine-grained soils by Refabricated Drains[J], Prec. 10th, (3), 1981, 677-682, Stockbolm. |
| [4] | Xie Kanghe, Zeng Guoxi, Consolidation Theories for Drain Wells under Equal Strain Condition[J], Chinese Joural of Geotechnical Engineering, 1989, 11(2): 3-17. (in Chinese) |
| [5] | Dong Zhiliang, Analytical Theory of Consolidation of Sand Drain’s Ground under Combined Vacuum and Surcharge Preloading[J], Port &Waterway Engineering, 1992, (9): 1-7. (in Chinese) |
| [6] | YIN Jing, LIU Shuguang, DONG Zhiliang, Three-dimensional Consolidation Analysis of Sand Drain’s Ground under Combined Vacuum and Surcharge Preloading Considering Loading Process[J], Joural of Tongji University (Natural Science), 2009, 37(9):1174-1225. (in Chinese) |
| [7] | Xiao-Wu Tang, Katsutada Onitsuka, Consolidation by Vertical Drains under time-dependent loading[J], Int. J. Numer. And Mech. Geomech.., 2000, 24:739-751. |
| [8] | Gong Xiaonan, Geotechnical Engineering of Computer Analysis [M], Beijing, China Architecture & Building Press, 2000. (in Chinese) |




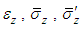 and
and 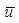 denote for the average strain, average total stress, average effective stress and average excess pore water pressure at the depth z, respectively, and mv is the coefficient of volume compressibility of soil. According to the above assumptions, the following equations can be got,
denote for the average strain, average total stress, average effective stress and average excess pore water pressure at the depth z, respectively, and mv is the coefficient of volume compressibility of soil. According to the above assumptions, the following equations can be got,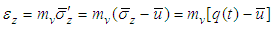
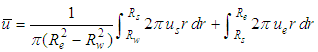
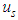 and
and 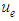 are the excess pore water pressure within the smeared zone and the undisturbed zone respectively. Taking Derivative of Eq.(1) with respect to t, the following equation is obtained,
are the excess pore water pressure within the smeared zone and the undisturbed zone respectively. Taking Derivative of Eq.(1) with respect to t, the following equation is obtained,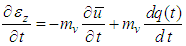
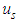 and
and 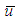 should satisfy the following equations:
should satisfy the following equations: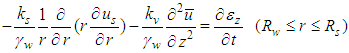
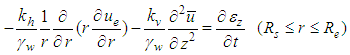
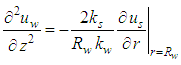
 is the pore pressure in the drain,
is the pore pressure in the drain,  is the unit weight of water. The solution conditions for the above Eqs. (1)~(6) are expressed asBoundary conditions:(1)
is the unit weight of water. The solution conditions for the above Eqs. (1)~(6) are expressed asBoundary conditions:(1) 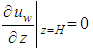 (The bottom of drain is impervious)(2)
(The bottom of drain is impervious)(2) 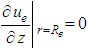 (The cylindrical surface of soil is impermeable)(3)
(The cylindrical surface of soil is impermeable)(3) 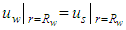 (Continuity of pore water pressure at
(Continuity of pore water pressure at 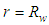 )(4)
)(4) 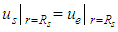 (Continuity of pore water pressure at
(Continuity of pore water pressure at 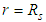 )(5)
)(5) 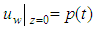 (Pore water pressure at the top of drain is equal to the vacuum preloading)Initial conditions:(1)
(Pore water pressure at the top of drain is equal to the vacuum preloading)Initial conditions:(1) 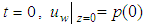 (2)
(2) 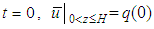 Integrating of Eqs.(4) and (5) with the boundary conditions (2), (3) and (4),
Integrating of Eqs.(4) and (5) with the boundary conditions (2), (3) and (4), 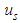 and
and 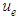 can be obtained as follows.
can be obtained as follows.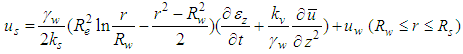
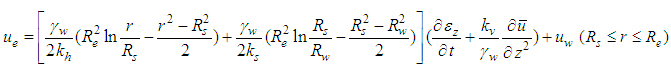
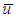 is presented,
is presented,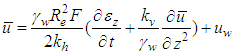
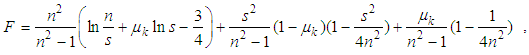
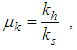
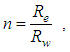
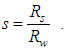 Substituting Eq. (7) into Eq.(6), the following expression can be obtained,
Substituting Eq. (7) into Eq.(6), the following expression can be obtained,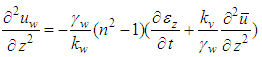
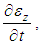 the following equation is got,
the following equation is got,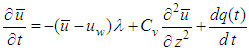
 and
and 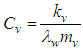 are the radial and coefficients of permeability of soil respectively. Combining with Eq.(9) and Eq.(10), and eliminating
are the radial and coefficients of permeability of soil respectively. Combining with Eq.(9) and Eq.(10), and eliminating 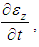 the following equation is obtained,
the following equation is obtained,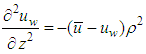
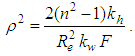 Combining with Eq.(11) and Eq.(12), and eliminating
Combining with Eq.(11) and Eq.(12), and eliminating 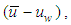 the following equation is got,
the following equation is got,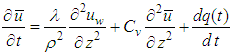
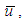 the equation about
the equation about 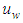 can be expressed as
can be expressed as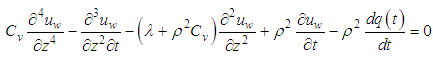
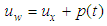
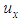 is called the transformed variable,
is called the transformed variable, 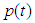 is vacuum preloading. Substituting Eq.(15) into Eq.(14), it can be rewritten as
is vacuum preloading. Substituting Eq.(15) into Eq.(14), it can be rewritten as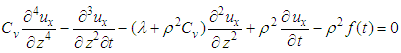
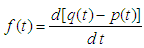
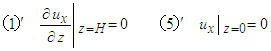 Using the separation of variables, and using the boundary conditions
Using the separation of variables, and using the boundary conditions 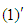 and
and 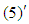 , the solution for Eq.(16) is
, the solution for Eq.(16) is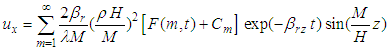
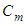 is an undetermined coefficient,
is an undetermined coefficient, 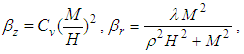
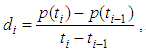
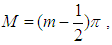
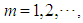 and
and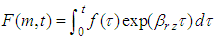
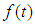 is expressed as Eq.(17). Substituting Eq. (18) into Eq.(15), the solution for
is expressed as Eq.(17). Substituting Eq. (18) into Eq.(15), the solution for 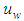 is
is 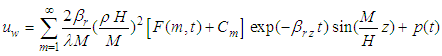
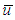 is
is 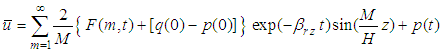
 can be determined as follows.
can be determined as follows.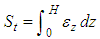
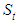 is expressed as
is expressed as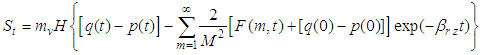
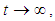 the ultimate vertical displacement at the top of soil,
the ultimate vertical displacement at the top of soil, 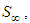 can be got from Eq.(23) as
can be got from Eq.(23) as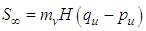
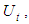 is defined as follows.
is defined as follows.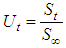
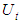 can be expressed as
can be expressed as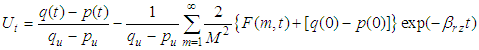
 is expressed as Eq.(19).
is expressed as Eq.(19). the vacuum preloading p(t) and surcharge preloading q(t) can be expressed as
the vacuum preloading p(t) and surcharge preloading q(t) can be expressed as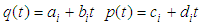
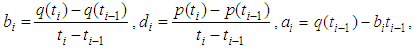
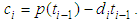 If
If 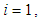 then
then 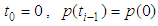 ,
,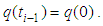 Note that when
Note that when 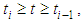 Eq.(19) can be expressed as
Eq.(19) can be expressed as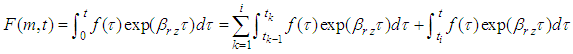 Substituting Eq.(27) into the above equation,
Substituting Eq.(27) into the above equation, 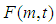 can be rewritten as
can be rewritten as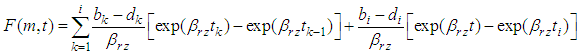 Substituting the above equation into Eq.(26), the average degree of consolidation
Substituting the above equation into Eq.(26), the average degree of consolidation 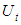 for linear multi-loading can be expressed as
for linear multi-loading can be expressed as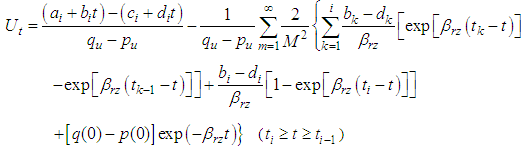

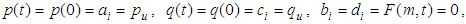 Eq.(28) becomes
Eq.(28) becomes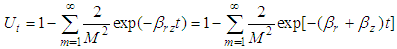
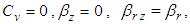 Eq.(29) is identical to Dong Zhi-liang’s formulation [5].If the radial flow is ignored, that is
Eq.(29) is identical to Dong Zhi-liang’s formulation [5].If the radial flow is ignored, that is 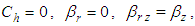 Eq.(29) degenerates into
Eq.(29) degenerates into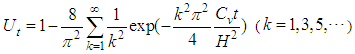
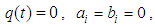 Eq.(28) degenerates into
Eq.(28) degenerates into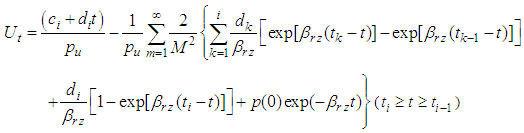
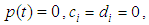 Eq.(28) degenerates into
Eq.(28) degenerates into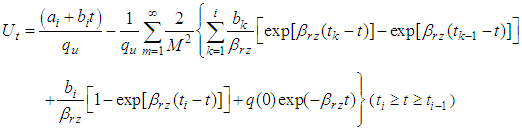
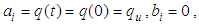 Eq.(32) is same as to Eq.(29). Besides, if vertical flow is ignored, that is
Eq.(32) is same as to Eq.(29). Besides, if vertical flow is ignored, that is 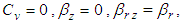 Eq.(32) becomes
Eq.(32) becomes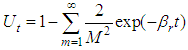
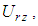 can be determined according to Carrilo’s method.
can be determined according to Carrilo’s method.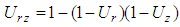 Where
Where 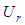 and
and 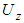 are the overall degree of consolidation for radial and vertical flow respectively. It is usually considered that Carrilo’s method is valid under time-independent loading (i.e., instantaneous loading). Under this condition, let
are the overall degree of consolidation for radial and vertical flow respectively. It is usually considered that Carrilo’s method is valid under time-independent loading (i.e., instantaneous loading). Under this condition, let 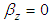 and
and 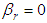 in Eq.(29) respectively,
in Eq.(29) respectively, 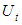 in the equation denotes for the degree of consolidation without vertical and without vertical flow
in the equation denotes for the degree of consolidation without vertical and without vertical flow 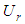 and
and 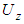 respectively. Obviously
respectively. Obviously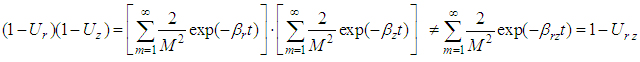 It is concluded that Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain because the average pore pressure
It is concluded that Carrillo’s method is not directly used to calculate the degree of consolidation for soils by vertical drains under the condition of equal vertical strain because the average pore pressure 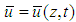 is adopted in Eqs.(4) and (5) according to the assumption of equal vertical strain.
is adopted in Eqs.(4) and (5) according to the assumption of equal vertical strain.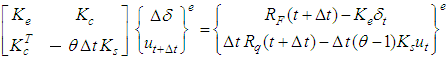
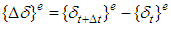 is the increments of nodal displacements in a element,
is the increments of nodal displacements in a element, 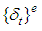 and
and 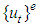 are the nodal displacements and nodal pore pressures at respectively,
are the nodal displacements and nodal pore pressures at respectively, 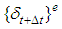 and
and 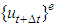 are the nodal displacements and pore pressures at
are the nodal displacements and pore pressures at 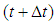 respectively,
respectively, 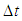 is time interval,
is time interval, 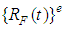 is nodal forces at t,
is nodal forces at t, 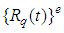 is nodal discharge matrix at t, and usually is zero [8].
is nodal discharge matrix at t, and usually is zero [8]. 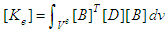 ,
, 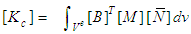 and
and 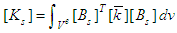 are the element stiffness matrix, element coupled matrix and element seepage matrix respectively,
are the element stiffness matrix, element coupled matrix and element seepage matrix respectively, 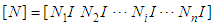 and
and  are the shape function matrixes for displacement and pore pressure respectively, I is a
are the shape function matrixes for displacement and pore pressure respectively, I is a 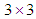 unit matrix,
unit matrix, 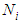 and
and 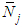 are the shape functions for displacement and pore pressure respectively, n and m are the total nodal numbers of displacement and pore pressure in a element respectively, {M}={1 1 1 0 0 0}T,
are the shape functions for displacement and pore pressure respectively, n and m are the total nodal numbers of displacement and pore pressure in a element respectively, {M}={1 1 1 0 0 0}T,  is an integral constant, and usually 0.5 or 2/3,
is an integral constant, and usually 0.5 or 2/3,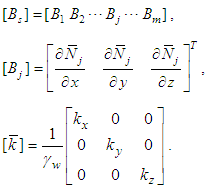 The assumed data for the verification are: Rw=5cm, Rs=2Rw, Re=20Rw, kw=2
The assumed data for the verification are: Rw=5cm, Rs=2Rw, Re=20Rw, kw=2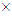 10-2cm/s, ks= 6
10-2cm/s, ks= 6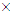 10-8cm/s, kh=kv=ks; mv=5
10-8cm/s, kh=kv=ks; mv=5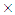 10-4kPa-1, elastic modulus E=1246.15kPa and Poisson’s ratio μ=0.35.The one-eighth of soil is considered because of its symmetry. The soil is vertically divided into some layers, and the elements in a layer are shown in Fig.4. The length of the drain, H=10m, is considered, and three cases: (1) vacuum loading only, (2) surcharge loading only and (3) combined vacuum and surcharge loading, are analyzed. Pentahedron element with 15 displacement nodes and 6 pore pressure nodes for the drain, and hexahedron element with 20 displacement nodes and 8 pore pressure nodes for the smeared zone and undisturbed zone, are used for the analysis.
10-4kPa-1, elastic modulus E=1246.15kPa and Poisson’s ratio μ=0.35.The one-eighth of soil is considered because of its symmetry. The soil is vertically divided into some layers, and the elements in a layer are shown in Fig.4. The length of the drain, H=10m, is considered, and three cases: (1) vacuum loading only, (2) surcharge loading only and (3) combined vacuum and surcharge loading, are analyzed. Pentahedron element with 15 displacement nodes and 6 pore pressure nodes for the drain, and hexahedron element with 20 displacement nodes and 8 pore pressure nodes for the smeared zone and undisturbed zone, are used for the analysis.
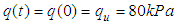 and
and 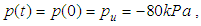 the comparisons between the calculated degree of consolidation by the FEM and got one from Eq.(26) are shown in Fig.5. It is clearly evident that both are in good agreement.
the comparisons between the calculated degree of consolidation by the FEM and got one from Eq.(26) are shown in Fig.5. It is clearly evident that both are in good agreement.


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML