-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2016; 6(2): 23-31
doi:10.5923/j.jce.20160602.01

Reliability Analysis of Bearing Capacity of Inclined Prestressed Concrete Pipe Pile
Li-Yun Tang , Jie Wang , Geng-She Yang , Yan-Jun Shen , Pei-Yong Qiu , Hui Liu
Xi'an University of Science & Technology, School of Architecture and Civil Engineering, Xi’an, China
Correspondence to: Li-Yun Tang , Xi'an University of Science & Technology, School of Architecture and Civil Engineering, Xi’an, China.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The incline of a prestressed concrete pipe pile induced by the incorrect excavation and incorrect heap of soil will change pile behavior and thus present a problem for determining the bearing capacity of the inclined pile. Aiming to solve this problem by analyzing the failure mechanism of inclined piles, the failure modes of inclined prestressed concrete pipe piles are divided into flexure failure and shear failure to establish the limit state equations accordingly. Based on structural reliability theory, by introducing JC-Method, a new method to calculate the reliability index of bearing capacity of inclined pile is proposed by MATLAB programming and the bearing feature of inclined pile is discussed. Combining with practical engineering, it’s concluded that the main factors affecting the reliability index of inclined pile bearing capacity are pile side resistance, pile declination and external diameter. Also, there exists specific thresholds of wall thickness and prestress that allows the reliability index of an inclined pile bearing capacity to change acutely when wall thickness or prestress is less than the specific threshold. In particular, the side resistance and tip resistance most obviously affects the reliability index of inclined pile bearing capacity when the slope of the line is smaller than 0.04. The main factor that affects bearing capacity of an inclined pile is the cracking bending moment when the load is lower than 1300kN.
Keywords: Inclined pile, Concrete pipe pile, Bearing capacity, Reliability index
Cite this paper: Li-Yun Tang , Jie Wang , Geng-She Yang , Yan-Jun Shen , Pei-Yong Qiu , Hui Liu , Reliability Analysis of Bearing Capacity of Inclined Prestressed Concrete Pipe Pile, Journal of Civil Engineering Research, Vol. 6 No. 2, 2016, pp. 23-31. doi: 10.5923/j.jce.20160602.01.
Article Outline
1. Introduction
- In recent years, the prestressed concrete pipe pile has been widely used in the construction of railway, highway, port and other structures. At the same time, the incline of the pile induced by the incorrect excavation and incorrect heap of soil will even exceed the upper limit of 1% stipulated in the specification [1]. Economic losses can be significant when the piles having inclines exceeding 1% are treated as discarded piles. In addition, the stress mechanism of inclined piles is very complicated with influences resulting from the vertical load, horizontal load or inclined load simultaneously. There is no unified method to assess the bearing capacity of piles where inclination exceeds 1%, thus it is important to study the behaviors of pile bearing capacity and contribute to the theoretical research for inclined pile design.The laboratory test and numerical analysis are the most widely used methods to analyze the inclined pile bearing capacity. Meyethof and Sastry [2] analyzed the deformation of piles with the influence of inclined loads and eccentric loads, and established an empirical formula for the relationship between ultimate shear and ultimate moment. Meyethof and Yalcin [3] also conducted tests to analyze the deformation characteristics of inclined piles when considering the influence of inclined load. Characteristic curves reflecting the change of the horizontal displacement of the pile tops with the change of the loads were obtained for when the piles are in different conditions of inclination. By conducting physical model tests. Long-qi Li et al. [4] concluded that the angle of the inclined pile is the main factor to change the pile bearing capacity, meanwhile Chandra Shekhar Goit et al. [5] and Nikos Gerolymos et al. [6] found that the Horizontal impedance functions of inclined single piles are smaller than the vertical pile and the values decrease as the angle of the pile inclination increases by Model tests and numerical analyses. Gang Zheng et al. [7] presented model test results studying the bearing capacity behaviors of inclined piles with different inclinations under vertical load and concluded that the bending failure of piles will occur when the degree of the pile inclination exceeds 8 degrees. Ashraf Nazir et al. [8] proposed that under the same inclination situations observed in modeling tests that the circular pile is more resistant to pullout forces than the square and rectangular pile shapes. The effect of inclination on the dynamic response of pile was analyzed by L. A. Padrón et al. [9, 10] and Cristina Medina et al. [11] and the settlement of a partially inclined pile was analyzed using finite element software by Li Wang et al. [12]. In addition, inclination is the most effective parameter in interaction factors of piles group with inclined piles [13, 14]. In conclusion, these studies have mainly focused on the effect of declination on the capacity of the pile, and few research are found reporting analyses of the influence from other factors, such as soil properties, load effect, pile material and diameter. Moreover, it’s well known that these factors do not function independently, but work synergistically [15]. The probabilistic method is introduced to analyze the effect of these factors on the capacity of inclined pile using reliability theory.At present, many researchers mainly focus on the vertical piles to analyze the reliability index of bearing capacity. Zi-fu Zhang et al. [16] has analyzed the influences of the pile side resistance, load effect on the reliability index, and proposes that the reliability degree meets the needs of the present codes when the coefficient of variation is within 0.2. Garland L et al. [17] and Niandou et al. [18] and ZHANG L M et al. [19, 20] propose that the ratio of test data to design data for bearing capacity have an obvious effect on the capacity reliability of inclined pile. The effect of soil properties on the capacity reliability has been study by Hai jian Fan et al. [21] and Ana Teixeiraa et al. [22], In addition, other researchers (Zhao et al. [23]; Zhao et al. [24]; Xu and Zhang [25]; Xu et al. [26]; Bian et al. [27] and Peter Friis Hansen [28]) have investigated the reliability index of the capacity of vertical piles through different computation methods by considering the failure criterion and load effects. However, there are few investigations about the reliability index of bearing capacity for an inclined pile, mainly because the bearing capacity formula for an inclined pile has not been consistently stipulated, and the limit state equations are difficult to establish when calculating the reliability of inclined pile. Additionally, little information has been found in the literature on estimating the reliability of inclined pile capacity. That is not surprising since the formulas of bearing capacity are not stipulated in the specification and the limit state equation of reliability theory is difficult to establish. This has thus caused the reliability analysis of bearing capacity of inclined pile to be difficult to achieve.Aiming to solve this problem by analyzing the failure mechanism of inclined piles, the failure modes of inclined prestressed concrete pipe pile are divided into flexure failure mode and shear failure mode, and the limit state equations are established accordingly. Based on structural reliability theory, by introducing JC-Method, a new method to calculate the reliability index of bearing capacity of inclined pile is proposed by MATLAB programming. The effect of the main factors on the bearing capacity with different inclinations and different loads is discussed, and this research makes a reference to the safety assessment of the inclined pile.
2. Failure Mode and Influential Factors of Inclined Piles
2.1. Failure Mechanism of Inclined Piles
- The limit state equations of JC-Method are established based on the pile bearing capacity, however, the forced mechanism of inclined piles is so complex that there specific approaches do not exist for defining the formula to calculate the pile bearing capacity in the specification. It’s necessary to analyze the failure modes of inclined piles and confirm the pile failure mode. However, the inclined pile failure mode is different from that of the vertical piles. The vertical load P on the top of the pile is divided into an axial load Py and a lateral load Px. The bearing capacity of inclined pile mainly then depends on two aspects: the shear failure and the flexural failure modes in the inclined pile. The shear failure will be observed due to a load larger than pile capacity which includes the side resistance Qsk and tip resistance Qpk, as shown in figure 1(a). The flexural failure is usually observed in the inclined pile when the cracking bending moment Mcr is lower than the bending moment M, which is produced by the lateral loads Px and the horizontal resisting force Sx due to soil, as shown in figure 1(b).
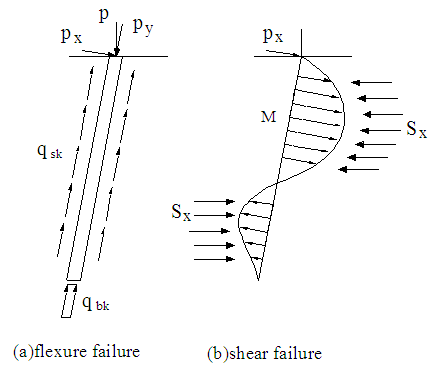 | Figure 1. Two kinds of failure pattern of batter pile |
2.2. Influential Factors of Inclined Piles
- The shear failure of an inclined prestressed concrete pipe pile is mainly due to the axial capacity being lower than the pile’s top axial loads. The axial capacity of single pile includes the side resistance and the tip resistance. The pile diameter affects the side resistance of pile, which is influenced by the surrounding soil properties. The primary factors affecting the pile shear failure include the side resistance, the tip resistance, the pile diameter and the pile’s top axial load.The flexural failure of inclined prestressed concrete pipe pile is mainly due to the cracking bending moment Mcr when it is lower than the bending moment M. The bending moment that is produced by the pile’s top lateral loads and the horizontal resisting force induced by the soil is affected by the declination and the lateral load. The cracking bending moment is determined by concrete strength and prestress conditions. Thus, the primary factors effecting flexural failure of an inclined pile include pile’s top lateral load, inclination, concrete strength and prestress conditions.
3. Reliability Theory of a Single Inclined Pile
3.1. Limit State Equations of Two Failure Modes
- It’s assumed that the performance function is only related to pile’s top load effect S and pile bearing capacity R. The performance function of an inclined pile can be written as
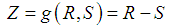 | (1) |
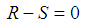 | (2) |
3.1.1. Limit State Equations of Flexure Failure Mode
- Considering that the pile can become inclined after piling, the tips of inclined pile and straight pile are in the same bearing stratum, so the design value of axial capacity of inclined pile can be written as:
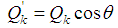 | (3) |
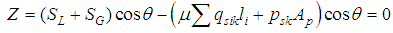 | (4) |
3.1.2. Limit State Equations of Shear Failure Mode
- The maximum bending moment under a vertical load and considering the
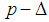 effect has been proposed by Ning [29] as follows :
effect has been proposed by Ning [29] as follows :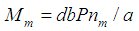 | (5) |
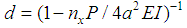 ; nx is the coefficient of the lateral deformation of the pile top, nx = 2.441 (pile length>a/4); P is the working load; a is the coefficient of pile horizontal deformation with
; nx is the coefficient of the lateral deformation of the pile top, nx = 2.441 (pile length>a/4); P is the working load; a is the coefficient of pile horizontal deformation with 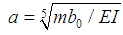 ; m is the proportional coefficient of side resistance and m can be defined as
; m is the proportional coefficient of side resistance and m can be defined as 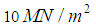 when the soil is a cohesive soil or dense silt; b0 is the calculated width of single pile; E is the elastic modulus of concrete; I is the inertia moment of the pile section; b is the declination; P is the vertical load; nm is the coefficient of the pile’s maximum bending moment and nm = 0.78 (pile length>a/4 ).The cracking bending moment of a steel pipe pile can be expressed as
when the soil is a cohesive soil or dense silt; b0 is the calculated width of single pile; E is the elastic modulus of concrete; I is the inertia moment of the pile section; b is the declination; P is the vertical load; nm is the coefficient of the pile’s maximum bending moment and nm = 0.78 (pile length>a/4 ).The cracking bending moment of a steel pipe pile can be expressed as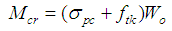 | (6) |
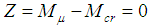 | (7) |
3.2. Random Variables of Two Limit State Equations
- The random variables include the length of pile, the sectional area of piles soil properties etc. which affect the reliability of inclined pile. In this article, the random variables are divided into resistance random variables and load random variables and each of random variables is analyzed.
3.2.1. Resistance Random Variables
- The parameters in the limit state equations, including the standard values of ultimate side resistance qsik , the standard values of ultimate tip resistance psk , the pipe pile prestress σpc, the standard values of the tensile strength of concrete ftk , the i layer of soil li , the area of pile bottom AD, the pile diameter μ and the outside diameter of pile D are all considered as resistance random variables. qsik and psk follow a normal distribution and the variation coefficient is between 0.1 and 0.3 [30]; the variation coefficient of σpc is 0.21; the variation coefficient of ftk is 0.18. μ, li , AD and D are considered as constants because the changes occurring with each of them is considered insignificant.
3.2.2. Load Random Variables
- The parameters in the limit state equations of the two failure modes including live load SL, dead load SG, amplifying coefficient of internal force and horizontal displacement d and declination b are considered as load random variables. Live load follows a normal distribution and dead load follows a logarithmic normal distribution. For convenience, the live and dead load effect is not considered individually, and the distribution characteristics of live load effect is equivalent to the distribution characteristics of pile’s top working load, namely the pile’s top load effect follows an approximate normal distribution and the coefficient of variation is 0.07 [31]. The amplifying coefficient of internal force and horizontal displacement d, the coefficient of the lateral deformation of pile top nx , the proportional coefficient of side resistance m, the calculative width of single pile b0 and the declination b are all considered as constants while the elastic modulus of concrete E and vertical load P are considered as random variables.
3.3. Reliability Calculation of Inclined Piles
- Based on limit state equations of inclined piles and statistics distribution of random variables, the JC method is introduced to analyze the reliability of the pile capacity. The linearization of functions is expanded on the structural failure hyperplane through a Taylor expansion by the JC method. The actual distribution of the random variables can be also considered by JC method.
3.3.1. Reliability Calculation under Flexure Failure Mode
- (1) qsik1, qsik2, qsik3, qsk and S follow a normal distribution. It is assumed that the checking points are known and the first order expansion of the performance function can be expressed as
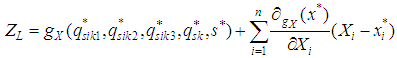 | (8) |
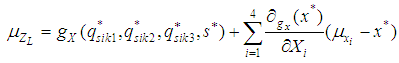 | (9) |
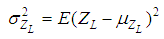 | (10) |
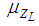 is the mean;
is the mean; 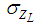 is the standard deviation.The reliability index can be formulated as
is the standard deviation.The reliability index can be formulated as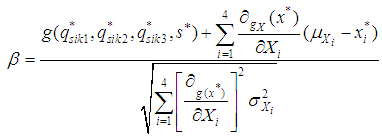 | (11) |
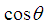 of coordinate vector corresponding to the normal of checking point P* in the limit state surface can be formulated as:
of coordinate vector corresponding to the normal of checking point P* in the limit state surface can be formulated as: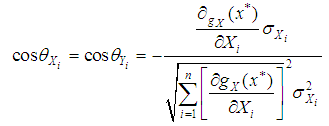 | (12) |
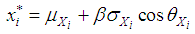 | (13) |
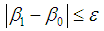 (tolerable error), the iteration is complete and the β1 is the ultimate reliability index; when
(tolerable error), the iteration is complete and the β1 is the ultimate reliability index; when 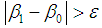 , the iteration continues by returning to step(3).
, the iteration continues by returning to step(3).3.3.2. Reliability Calculation under Bending Failure Mode
- (1) σpc,ftk , S follow a normal distribution. It’s assumed that the checking points are known and the first order expansion of performance function can be expressed as:
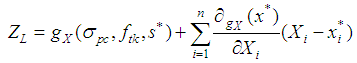 | (14) |
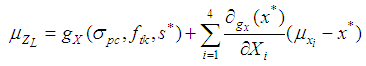 | (15) |
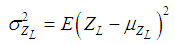 | (16) |
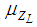 is the mean;
is the mean; 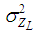 is the standard deviation.The reliability index can be formulated as:
is the standard deviation.The reliability index can be formulated as: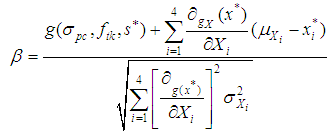 | (17) |
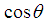 of coordinate vector corresponding to the normal of checking point P* in the limit state surface can be formulated as:
of coordinate vector corresponding to the normal of checking point P* in the limit state surface can be formulated as: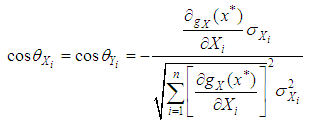 | (18) |
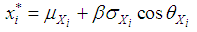 | (19) |
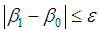 (margin for error), the iteration is complete and the β1 is the ultimate reliability index; when
(margin for error), the iteration is complete and the β1 is the ultimate reliability index; when 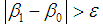 , the iteration continues by returning to step(3).
, the iteration continues by returning to step(3).4. Validation by Practical Engineering
4.1. Engineering Situation
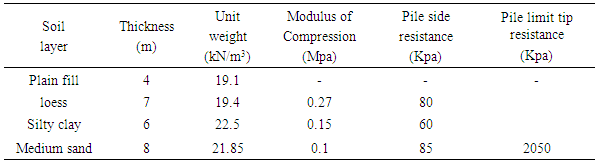
- The above-ground building of 1# building of Xi’an Beibuwan project is a reinforced concrete shear wall structure with a pile-raft foundation used in the infrastructure. High strength pre-stressing concrete piles (PHC) are used in the foundation. The diameter of the pile is 600mm; the pile length is 21m; the wall thickness of the pile is 110mm; the concrete strength grade is C50, and the prestress is 6 MPa. According to the geological data, the physical and mechanical parameters of the soil are shown in table 1.
|
4.2. Random Variables Influence on Reliability Index
- Since changes in the random variables will cause changes in the reliability index during reliability analysis, controlling variables is the method used to analyze the random variables, including the influence that variable coefficient of pile side resistance and tip resistance has on the reliability index, as well as declination, wall thickness, load effect, etc. The influence of the random variables on the reliability index is also analyzed.
4.2.1. Effect of Variable Coefficient of Pile Side Resistance and Tip Resistance on Reliability Index
- In shear failure mode, there is a significant influence of the pile side resistance and tip resistance on the pile axial bearing capacity. In this project the first soil layer is a plain fill so the pile side resistance can be neglected. Keeping other random variables unchanged, when the variable coefficients of pile side resistance and tip resistance in the different soil layers change from 0.05 to 0.25, the pile reliability indexes are calculated and the results are shown in figure 2.
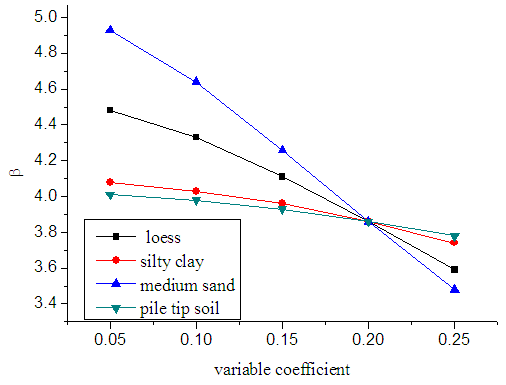 | Figure 2. Effect of variable coefficient of pile side resistance and tip resistance on reliability index |
4.2.2. Effect of Pile Declination on Reliability Index
- Declination has a significant effect on the reliability index of an inclined pile. Keeping all other random variables unchanged, the influence of declinations ranging from 0.01 to 0.08 on the reliability indexes of inclined piles are analyzed and shown in table 2.
|
4.2.3. Effect of Prestress on Reliability Index
- Keeping other random variables unchanged, when the prestress ranges from 1MPa to 10MPa, the reliability indexes for the declination at 0.02 and 0.03 respectively, can be seen in figure 3.
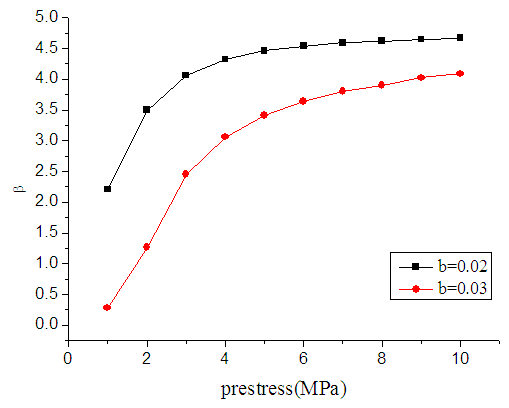 | Figure 3. Effect of prestress on reliability index |
4.2.4. Effect of Concrete Strength on Reliability Index
- Standard values of tensile strength of concrete will affect both the cracking bending moment of pipe pile, and the reliability index of an inclined pile. Usually C50~C80 concrete is used for steel pipe piles. Keeping other random variables unchanged, the influence of concrete strength ranging from C50 to C80 on the reliability indexes of inclined piles are analyzed and shown in table 3.
|
4.2.5. Effect of Wall Thickness on Reliability Index
- The wall thickness of the pipe pile will affect the elastic resistance moment of the tensile edge of conversed section of the pipe pile, and the reliability index as well. The influence of pipe pile wall thickness on the reliability index, is analyzed for piles with the declinations of 0.01, 0.03 and 0.06. Keeping other random variables unchanged, the effect on the reliability indexes is analyzed separately for wall thickness ranging from 70mm to 130mm, and is shown in figure 4.
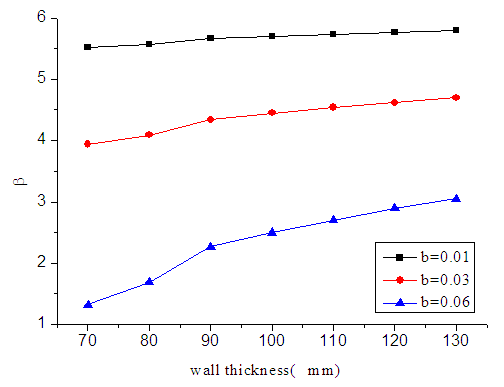 | Figure 4. Effect of wall thickness on reliability index |
4.2.6. Effect of External Diameter on Reliability Index
- Keeping other random variables unchanged, the reliability indexes of the two kinds of failure modes are obtained for when the external diameter ranges from 500 mm to 800 mm, and are shown in figure 5.
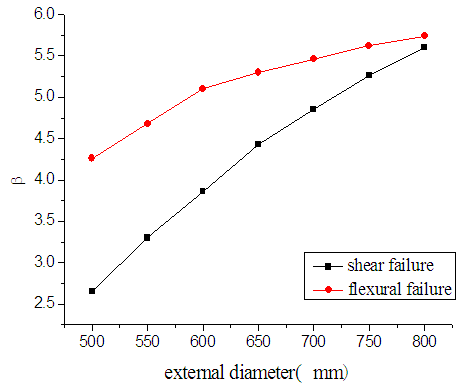 | Figure 5. Effect of external diameter on reliability index |
 | Figure 6. Effect of external diameter on reliability index |
4.2.7. Effect of Load Effect on Reliability Index
- Keeping other random variables unchanged, when external loads range from 1000kN to 3000kN, the reliability index for the shear failure and the reliability indexes of piles for when the declination changes from 0.01 to 0.05 in the flexural failure mode are analyzed and shown in figure 7.
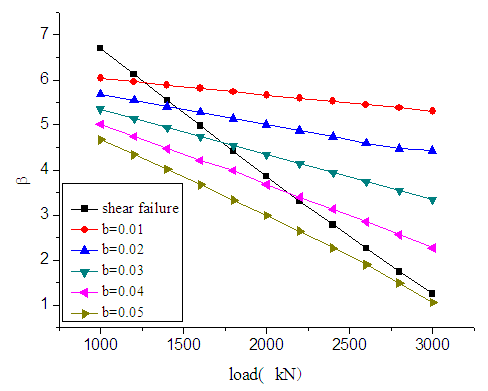 | Figure 7. Effect of load on reliability index |
5. Conclusions
- Based on the JC method and the MATLAB programming approach used, a new method to calculate the reliability index of an inclined pile is proposed, where the results may give a reference for use in following research studies of inclined pile reliability. According to the practical engineering project and analysis, the following conclusions were obtained:The effect of the variable coefficient of pile side resistance, declination and external diameter on the reliability index is more obvious, with the effect of external diameter on the reliability index in the flexural failure mode being more acute than that in shear failure mode.There exist threshold values of wall thickness and prestress. When the wall thickness or prestress is lower than the threshold value, the reliability index increases rapidly with the increase of the wall thickness or prestress respectively. When the wall thickness or prestress is greater than the threshold value, the reliability index slowly increases as the respective increase in wall thickness or prestress.There exists a critical declination which causes the pile side resistance and tip resistance to have a more obvious effect on the reliability index when the declination is lower than the critical declination. When the declination exceeds the critical declination, the effect of the cracking bending moment on the reliability index becomes more obvious.There exists a critical load which makes the cracking bending moment have a more obvious effect on the reliability index when the working load is lower than this critical load. When the working load exceeds the critical load the effect of pile side resistance and tip resistance on the reliability index becomes more obvious.From the conclusion above, some advice which is useful in the actual projects could be got:The effect of the external diameter on the reliability index is more obvious, so the bearing capacity of the inclined pile can be improved by appropriately increasing the external diameter of pile in the actual projects.The researches provide reference for the security of the inclined pile. From the research work above, the security of the inclined pile will not be impacted when the declination is lower than 0.04. On the basis of ensuring the project quality, the project budget can be reduced by using the threshold values of wall thickness and prestress in the actual projects according to the algorithm in this paper.
ACKNOWLEDGEMENTS
- This research was supported by the National Natural Science Foundation of China (No. 41502298), Shaanxi province science and technology innovation team project (No.2014KCT-30) and the Overall Innovation Projects of Science and Technology of Shanxi Province of China (No.2011KTZ03-02-01).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML