-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2015; 5(6): 162-171
doi:10.5923/j.jce.20150506.06

Simplified Nonlinear Analysis of Reinforced Concrete Slabs and Beams
Graham Dean Roberts1, Kuinian Li2
1Dams & Hydro, ARQ Consulting Engineers, Pretoria, South Africa
2School of Civil & Environmental Engineering, University of Witwatersrand, Johannesburg, South Africa
Correspondence to: Graham Dean Roberts, Dams & Hydro, ARQ Consulting Engineers, Pretoria, South Africa.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The use of the finite element method in the design of reinforced concrete slabs and beams has become a generally accepted practice in recent times and when designing structural members, both ultimate and serviceability limit states are required to be considered in the consequent analyses. This paper presents a simplified method to the nonlinear analysis of reinforced concrete slabs and beams for serviceability and ultimate limit states. The method allows for the use of simple design equations familiar to all structural engineers undertaking reinforced concrete designs. Using the finite element method, plate elements and simplified constitutive properties, a nonlinear algorithm is developed which results in the accurate estimation of the displacements during loading as well as a design ultimate loading. The proposed model and nonlinear algorithm is validated and verified against three experimental case studies which show the accuracy and relevance of the given nonlinear solution. The model and algorithm presented can be easily integrated into a commercial finite element package for use in the design of reinforced concrete slabs and beams.
Keywords: Nonlinear, Reinforced Concrete, Simplified, Finite Element Method, Design
Cite this paper: Graham Dean Roberts, Kuinian Li, Simplified Nonlinear Analysis of Reinforced Concrete Slabs and Beams, Journal of Civil Engineering Research, Vol. 5 No. 6, 2015, pp. 162-171. doi: 10.5923/j.jce.20150506.06.
Article Outline
1. Introduction
- The finite element method is widely used in modern day reinforced concrete slab and beam design using either plate or shell elements to represent the structural behaviour. Many commercial finite element software packages have design code checks to allow for the elastic analysis and design to be carried out using one software package. For certain packages a design code based approach to moment redistribution and serviceability deflection checks could be included. It is however not common for the standard finite element packages to carry out a more accurate numerical nonlinear analysis to account for moment redistribution and accurate serviceability deflection checks. The nonlinear behaviour of reinforced concrete is complex in nature and has been under consideration since mid-1960 through till today. The formulation of plate and shell elements began to be established in early 1960 and formulations improved rapidly through till late 1980. The evolution of both topics have taken place over a similar period and with the increase in computing power over the late 1980 early 1990 many researchers have developed separate constitutive numerical relations combined with plate and shell element formulations to mimic the nonlinear behaviour of reinforced concrete slabs.These methods however, such as the layered method given by Hu and Schnobrich (1990) [9], Zhang and Bradford and Gilbert (2007) [26] can be seen as complex to engineers not entirely familiar with the detailed theory of finite elements. Polak (1996) [16], introduced a less complex approach by using an effective Young’s modulus based on the effective moment of inertia equation given by Branson (1968) [5]. The method proposed by Polak allows for serviceability deflection checks only and requires the internal finite element solving procedure to be adjusted by enabling the calculation of an effective moment of inertia using averaged Gauss point moment results at each load step. This paper presents a simplified design approach to the nonlinear analysis and design of reinforced concrete slabs and beams. The approach allows for standard stress-strain relationships to be established using common reinforced concrete design equations. These stress-strain relations can be defined for each direction of reinforcement and used in the nonlinear analysis as would be done for typical orthotropic ductile materials. The method will allow for the easy implementation into most commercial finite element software packages with Application Programming Interface (API) capability.
2. Theoretical Finite Element Model
- To implement, validate and verify the simplified method of analysis, a finite element code is created, by the author, using MatLab R2011b. Elements are established in the form of 8-noded plate elements based on Mindlin-Reissner [19] [14] [20] formulation with three degrees of freedom per node as given in text by Bathe (1996) [4] and shown in Figure 1.
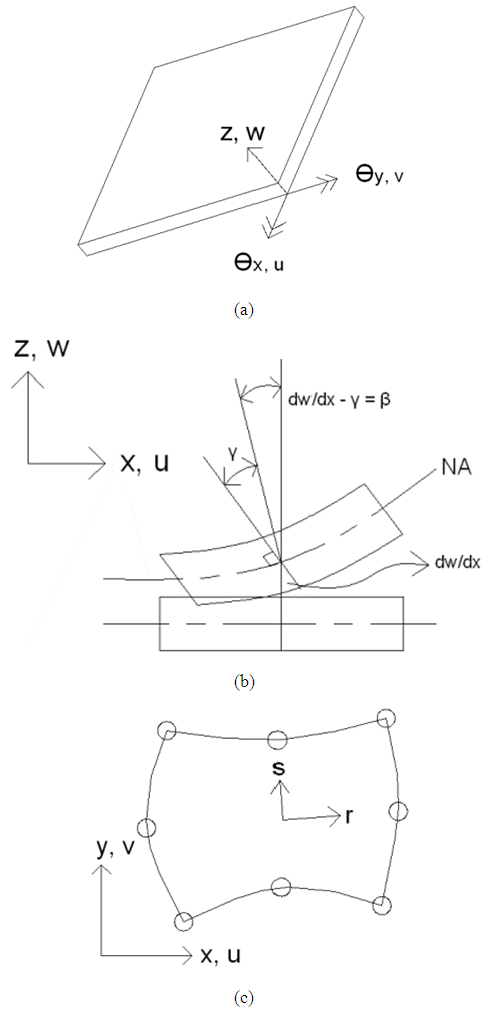 | Figure 1. (a) Nodal degrees of freedom (b) Bending & shear deformation (c) Isoparametric 8-noded plate element axis [19] [14] [20] |
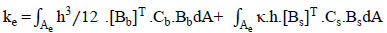 | (1) |
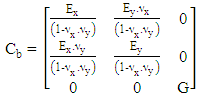 | (2) |
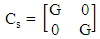 | (3) |
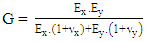 | (4) |
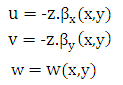 | (5) |
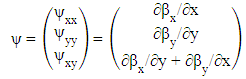 | (6) |
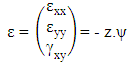 | (7) |
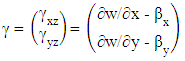 | (8) |
3. Material Properties
- The nonlinear reinforced concrete material constitutive relations are established with two objectives in mind. Firstly the material properties presented must have the required level of accuracy so as to validate its use in design methods and secondly to enable ease of formulation for the design engineer. In the derivation of the nonlinear material properties of the reinforced concrete, with regard to this paper, the following assumptions are made. Simple beam theory: Cross sections normal to the mid-plane of an element that are plane prior to loading and remain plane during the stress development process. This assumption is made for the formulation of thin plates and as thick plate theory is used in the finite element formulation in this paper, this assumption may affect behaviour. But as the theory is established for use in slab members, shear deformations are not expected to contribute significantly to the overall deformation of an element. Tension controlled reinforced concrete: Structural elements considered in the scope of this paper are considered to be tension controlled whereby the tensile reinforcement will reach yield strain prior to the onset of concrete compressive failure. This assumption is valid as slab designs should be carried out so as to ensure ductile failure modes. Tension control should in any case be checked in the design process.Linear strain distribution: Strains throughout the cross sectional depth are assumed to have a linear distribution. This has been shown to be a valid assumption when carrying out the analysis and design of reinforced concrete structures.Compatible strains: the reinforcement is assumed to have a perfect bond with the surrounding concrete. This is a common assumption in the design of reinforced concrete slabs.The nonlinear behaviour of reinforced concrete can be effectively depicted using the standard moment curvature relations and bending stiffness is therefore dependent on the slope of the moment curvature graph,
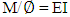 . When the section is loaded and as loading increases, the concrete in tension reaches the cracking strain and with increased loading cracking is initiated and propagation continues upward till the yielding and ultimate moments are reached.As the crack propagates upward, the section I value and therefore bending stiffness continues to change throughout the loading process. Through experimentation Branson (1968) [5] developed an equation to calculate the effective I value of a reinforced concrete beam and would enable the efficient calculation of section deflection and can be used to manually calculate deflections in structural systems. When carrying out the finite element analysis it is not practical to change the h value, as given in equation (1), which directly changes the I value of the section. It is more convenient and common to manipulate the bending stiffness through the changing of the E-modulus.The question then arises as to which stiffness states to consider. The three major states of moment capacity in a reinforced concrete section can be considered as the cracking moment, yielding moment and the ultimate moment.The E-modulus is defined as the tangent of a stress-strain relation. As the variation in bending stiffness will be manipulated using the E-modulus and the E-modulus is dependent on the relation of stress and strain, an equivalent stress-strain graph will be constructed to represent this variation in bending stiffness of the reinforced concrete section as shown in Figure 2.
. When the section is loaded and as loading increases, the concrete in tension reaches the cracking strain and with increased loading cracking is initiated and propagation continues upward till the yielding and ultimate moments are reached.As the crack propagates upward, the section I value and therefore bending stiffness continues to change throughout the loading process. Through experimentation Branson (1968) [5] developed an equation to calculate the effective I value of a reinforced concrete beam and would enable the efficient calculation of section deflection and can be used to manually calculate deflections in structural systems. When carrying out the finite element analysis it is not practical to change the h value, as given in equation (1), which directly changes the I value of the section. It is more convenient and common to manipulate the bending stiffness through the changing of the E-modulus.The question then arises as to which stiffness states to consider. The three major states of moment capacity in a reinforced concrete section can be considered as the cracking moment, yielding moment and the ultimate moment.The E-modulus is defined as the tangent of a stress-strain relation. As the variation in bending stiffness will be manipulated using the E-modulus and the E-modulus is dependent on the relation of stress and strain, an equivalent stress-strain graph will be constructed to represent this variation in bending stiffness of the reinforced concrete section as shown in Figure 2.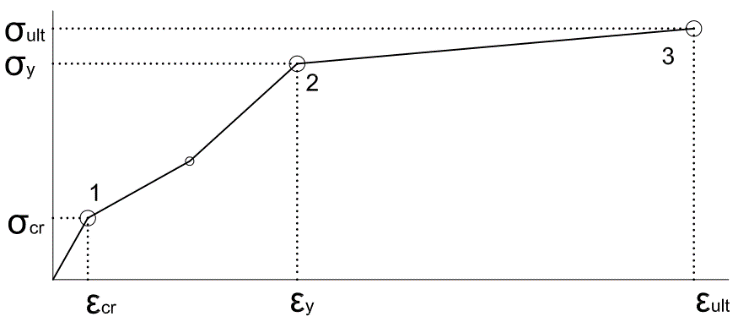 | Figure 2. Typical equivalent stress-strain graph |
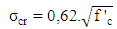 | (9) |
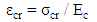 | (10) |
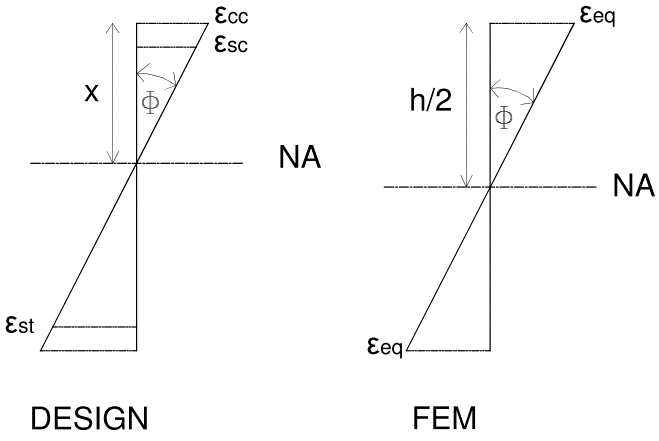 | Figure 3. Design strain state and equivalent finite element strain state |
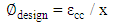 | (11) |
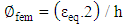 | (12) |
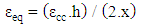 | (13) |
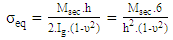 | (14) |
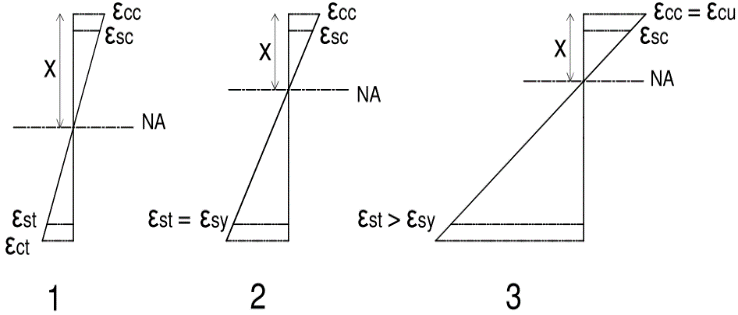 | Figure 4. Three major design strain states to be considered |
4. Nonlinear Solver Algorithm
- The proposed nonlinear solution considers only material nonlinearities and does not consider geometric nonlinearities as large displacements are not of concern for this particular application.As discussed in Section 2 the E-modulus of the material can be changed to give an equivalent bending stiffness to the plate formulation. Using the reinforcement properties of the concrete member, what is now termed strain control points making up a typical stress strain diagram can be established. This is assuming that the local x and y co-ordinates of the plate elements are aligned with the two directions of reinforcement and local co-ordinates results are used to assess nonlinearity.The overall solution is a nonlinear analysis, but the intermediate solution procedure is in essence a repetitive linear static solution updating the stiffness matrix after each converged load step. A converged load step is defined as one in which the applied loading at a given increment causes no strain at any one result point to exceed criteria and one or more to fall within the convergence criteria. For this procedure the convergence criteria is defined by equation (15) as given by Roberts (2014) [21].
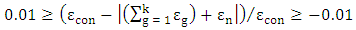 | (15) |
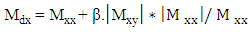 | (16) |
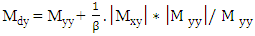 | (17) |
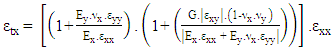 | (18) |
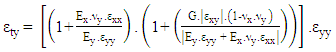 | (19) |
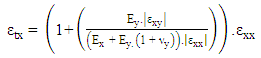 | (20) |
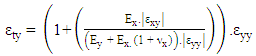 | (21) |
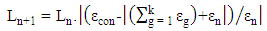 | (22) |
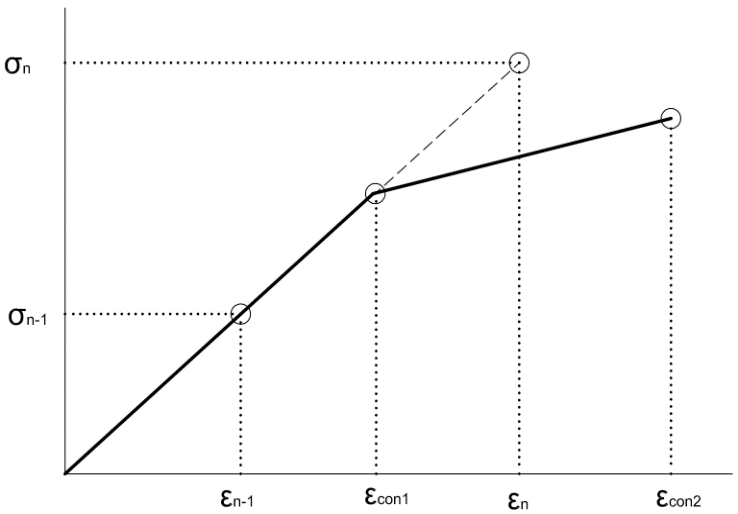 | Figure 5. Load increase / reduction logic |
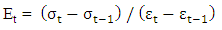 | (23) |
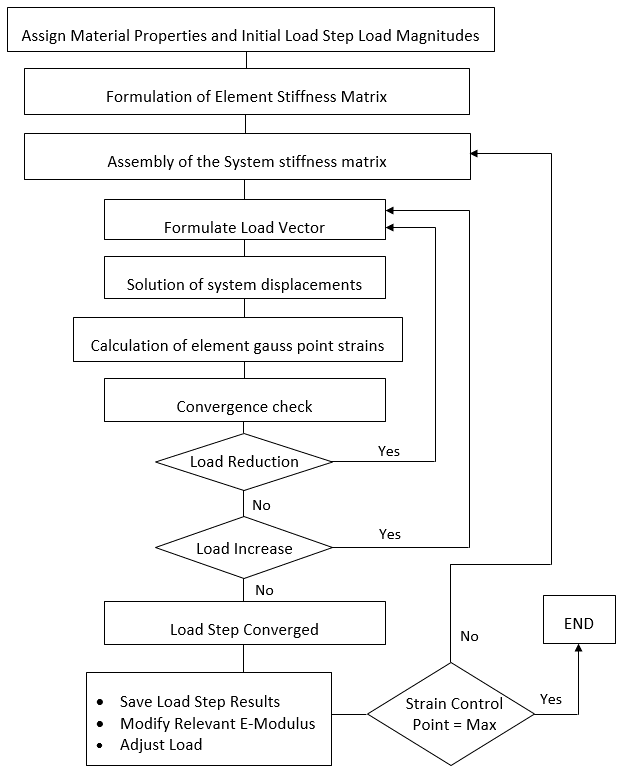 | Figure 6. Nonlinear algorithm |
5. Experimental Cases
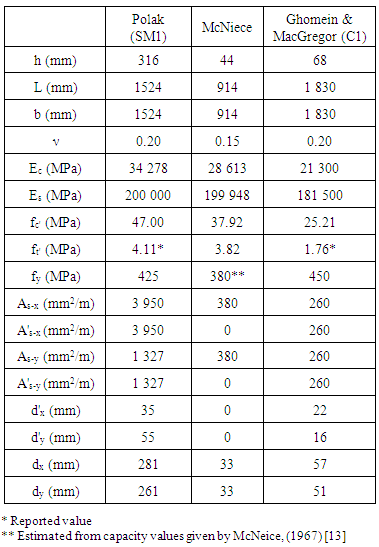
- To evaluate the appropriateness of the proposed method, three experimental test cases were evaluated. Firstly an experiment carried out by Polak and Vecchio (1994) [18] for test specimen SM1 was considered. In the experiment a one-way spanning slab was subjected to an increasing edge moment loading in one direction only, Figure 7(a). During the experiment cracking was reported at an applied moment of 75 kN.m/m with first yielding at a moment of 440 kN.m/m and the testing stopped at moment of 464 kN.m/m due to excessive deflections. Moment curvature results were established and are used for the current evaluation.
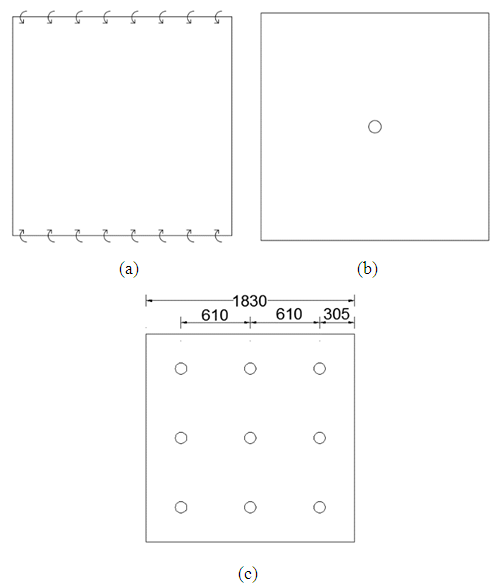 | Figure 7. Loading configuration (a) Polak and Vecchio (1994), SM1 (b) McNeice (1967) (c) Ghomein and MacGregor (1992), C1 |
6. Numerical Analysis
- The numerical analyses were carried out using 8-noded plate elements as described in Section 2. The SM1 slab was analysed using one plate element simply supported at the ends and edge moment loading applied. The McNeice and C1 slabs were analysed using an upper right quarter symmetry model discretised using nine plate elements as shown in Figure 8. For the McNeice slab the centre loading was represented by a single out of plain nodal load applied to node 7 and vertically restrained at node 34. For the slab C1 the loading was represented by applying out of plain proportional nodal load at nodes 3, 7, 25 and 29. Slab C1 was modelled as simply supported along the sides of non-symmetry.
 | Figure 8. Discretisation of McNeice and C1 slabs |
|
7. Analysis Results
- Following the analysis of the SM1 slab the moment and curvature results are extracted, Figure 9. Initial cracking occurred at a moment of 77 kN.m/m with the yielding moment at 425 kN.m/m. From the analysis the section ultimate moment was observed at 457 kN.m/m. Curvatures are seen to be accurate throughout the analysis. The analytical model continues to take loading until the design ultimate moment capacity, as per design equations, was reached.
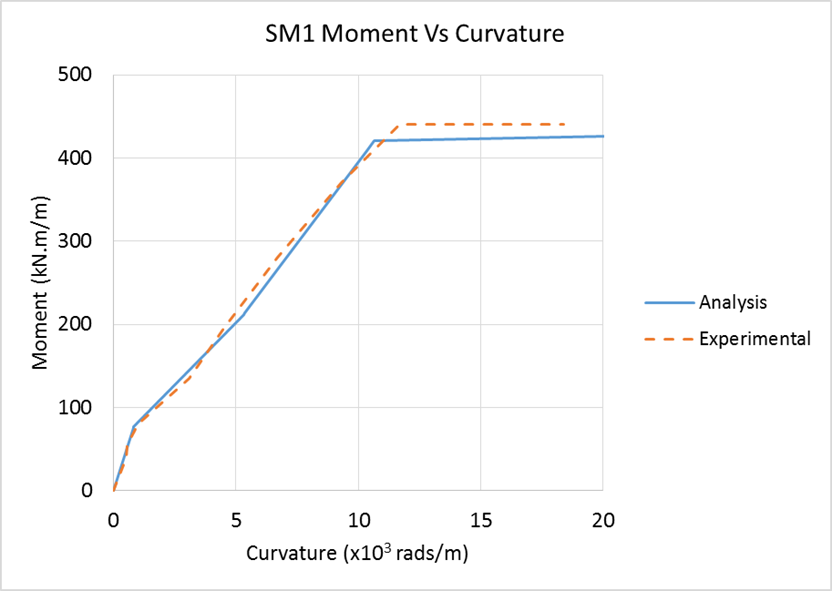 | Figure 9. SM1 Moment vs Curvature |
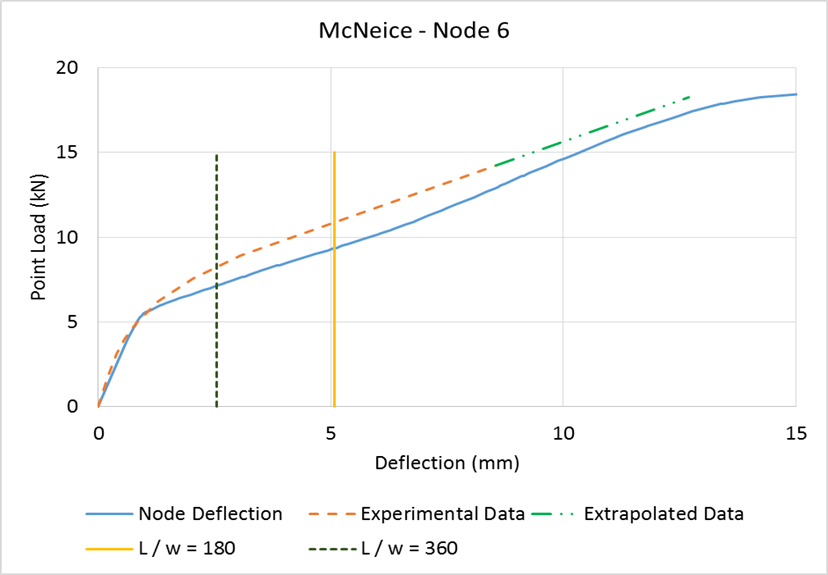 | Figure 10. McNeice Node 6 Load vs Displacement |
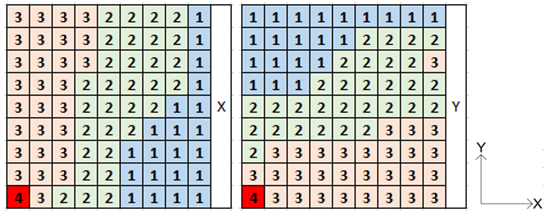 | Figure 11. McNeice slab cracking in the x and y directions |
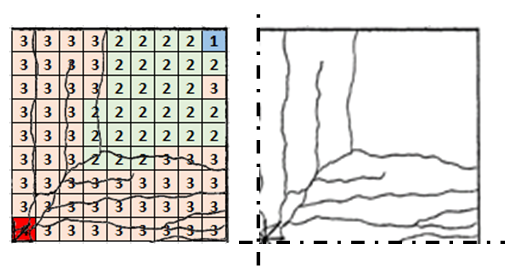 | Figure 12. McNeice crack pattern comparison |
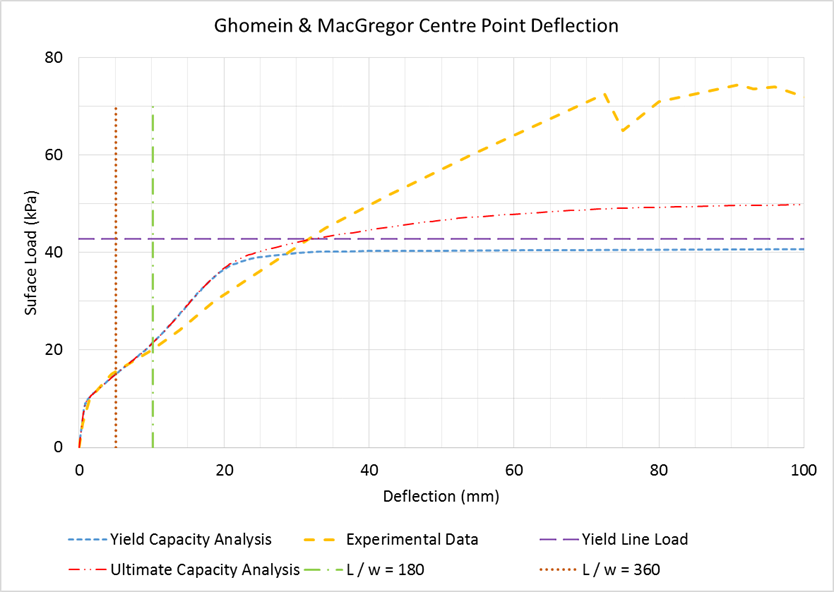 | Figure 13. C1 Load vs Displacement |
8. Conclusions
- The reinforced concrete slab nonlinear material properties are based on design code calculations. The nonlinear material properties are established for the x and y orthogonal directions of reinforcement independent of one another. Using these quantities typical stress-strain relations are formulated for the use in a nonlinear finite element analysis.A solution algorithm considering material nonlinearity is presented giving a simple linear finite element program, with API capabilities, the ability to solve the nonlinear problem described in this paper. Although any existing nonlinear algorithm may be utilised for the solution, it should ensure that the updating of the stiffness matrix is carried out using the methods and criteria described in this paper.Verification and validation was carried out considering three experimental case studies. These experimental case studies ensured that a variety of loading types and boundary conditions are tested against the proposed analytical model. The overall displacement results obtained through the various analyses can be considered sufficiently accurate for serviceability checks under design conditions.If the design of reinforced concrete slabs is to be carried out assuming ductile yield failure as would usually be done, the proposed model would produce valuable and accurate moment distribution and displacement predictions. The method is however not suitable for forensic structural analysis where actual failure mechanisms are required.Although results and stiffness values were checked and assigned at element Gauss points independently, a different approach may be followed whereby the Gauss point results are checked and an average element stiffness value calculated and assigned at element level for each direction of reinforcement respectively. This decision would depend on the fineness of the discretisation which should be able to sufficiently represent the distribution of yielding throughout the slab.Although not considered in this paper, continuous slabs can be seen to be analysed by extending the typical stress-strain graph to include the reinforced concrete slab section negative moment capacities for cracking, yield and ultimate in the same manner as described in the paper. By extending the typical stress-strain diagram any negative moments experienced by the slab, whereby the top of the slab is in tension, can be considered independently and with ease. By using this method accurate moment redistribution results can be established. This should however still be verified with experimental data prior to implementation. The benefit of the proposed model is that the nonlinear behaviour of a slab is based on a design code approach which closely relates analytical results to the real-life structural system behaviour. The simplified method can therefore easily form part of a design report with engineer’s calculations and not merely a theoretical model built into a finite element program which the design engineer is not fully comfortable with or knowledgeable about.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML