-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2015; 5(5): 118-123
doi:10.5923/j.jce.20150505.04
Scattering of Anti-Plane Waves by a Sloping U-Shaped Canyon
Wen-Shinn Shyu1, Chuen-Shii Chou2
1Department of Civil Engineering, National Pingtung University of Science and Technology, Taiwan
2Department of Mechanical Engineering, National Pingtung University of Science and Technology, Taiwan
Correspondence to: Wen-Shinn Shyu, Department of Civil Engineering, National Pingtung University of Science and Technology, Taiwan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The response of surface motion on and near a sloping U-shaped canyon on elastic half-plane is investigated for the case of incident anti-plane waves. A sloping U-shaped canyon is a kind of surface irregularity. For the problem of incident anti-plane waves, it is the simplest form of excitation. Exact analytical solution of U-shaped canyon problem was formulated by use of a series solution by Guo et al. on 2012. The scattering problems of a shallow sloping U-shaped canyon and a deep sloping U-shaped canyon had to discuss in this study. Hybrid method combines the finite element with series expansion method. The hybrid method is suitable to solve the scattering problem by surface irregularities, such as a canyon, a basin or a hill. The merit of the hybrid method is that the flexibility of finite elements offers the greatest advantage to model the surface irregularity. The unknown boundary data called the scattered waves can be formulated through a series representation with unknown coefficients. Due to the continuity condition at the interface, the unknown coefficients of this series representation are treated as generalized coordinates. The expansion function of the series representation is constituted of basis functions, each basis function is constructed by Lamb’s solution and satisfies both traction free condition at ground surface and radiation condition at infinity. In this paper, we define a substructure which enclosing the sloping U-shaped canyon. So the scattering problem of half space is simplified as a region meshed problem by finite elements. The transfinite interpolation (TFI) provides excellent mesh grids on the irregular domain. The node numbers of the finite elements and the arrangement of the elements are the same as a shadow sloping U-shaped canyon or a sloping U-shaped canyon. The hybrid method provides a simple and systematical method to solve the scattering problem by surface irregularities.
Keywords: Anti-Plane wave, Scattering problem, Sloping U-Shaped canyon, Hybrid method, Transfinite interpolation
Cite this paper: Wen-Shinn Shyu, Chuen-Shii Chou, Scattering of Anti-Plane Waves by a Sloping U-Shaped Canyon, Journal of Civil Engineering Research, Vol. 5 No. 5, 2015, pp. 118-123. doi: 10.5923/j.jce.20150505.04.
Article Outline
1. Introduction
- A surface irregularity, such as a canyon, can raises large amplifications in ground motion during earthquakes. The seismic response information of a canyon will be helpful in the aseismatic design. The behavior of seismic responses is a kind of wave scattering and diffraction problem. The simplest form in this study is incident SH waves excitation cause of no mode conversion. Problems of the scattering of plane SH waves have been discussed over the last four decades. Canyon is the simplest form of the surface irregularities and discussed first. From early ‘70s, Trifunac obtained exact analytical solutions for the scattering of plane SH waves from a two-dimensional semi-cylindrical canyon [1], and semi-elliptical canyon [2], and Yuan et al. discussed a circular-arc cross-section canyon [3]. For a simple geometric shape, such as a semi-circular canyon or a semi-elliptical canyon, the wave function expansion methods are obtained by the separation of variables and the solution is shown in orthogonal basis functions. Otherwise, additional technique is necessary to solve the scattering problem, such as Tsaur et al. used a selection of the auxiliary boundary and Graf’s addition formula to solve the scattering problem of V-shaped canyon [4, 5] and truncated semicircular canyon [6]. Zhang et al. solved the V-shape canyon [7] and U-shaped canyon [8]. To solve the problem of scattering by an irregularity, various techniques have been proposed, such as Chen et al. used a semi-analytical approach technique to solve the problem due to multiple canyons [9]. Mei developed a variational formulation to solve a radiation problem [10]. Based on his work, Yeh et al. utilized a hybrid method of the finite element method and the series expansion to solve radiation problem in an elastic half-plane [11]. The hybrid method can be used easily solve problems that involve the scattering of SH waves by irregular canyons. The main disadvantage of the hybrid method is the difficulty of discretizations on the domain that encloses the irregularity. To overcome this disadvantage, transfinite interpolation is adopted to mesh the domain of irregularity [12]. Cases of an irregular canyon subject to SH waves were also studied [13-15]. In this study, the author uses the hybrid method to solve the scattering of anti-plane waves by a sloping U-shaped canyon, and a trapezoid canyon as a special case is also discussed.
2. Problem Description
- Figure 1 (a) presents a 2D model, which consists of a sloping U-shaped canyon embedded in the half-space and is excited by a unit-amplitude plane SH wave with circular frequency
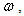 incident angle
incident angle 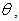 and displacement in the y-direction. The width of the symmetrical sloping U-shaped canyon, the width of the canyon bottom and depth are
and displacement in the y-direction. The width of the symmetrical sloping U-shaped canyon, the width of the canyon bottom and depth are 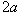 , 2b and d (where
, 2b and d (where 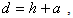 h is a depth parameter), respectively. Let the elastic half-plane be divided into
h is a depth parameter), respectively. Let the elastic half-plane be divided into 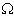 and
and 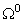 by a semi-circular interface C.
by a semi-circular interface C. 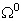 is a finite domain that encloses the sloping U-shaped canyon.
is a finite domain that encloses the sloping U-shaped canyon.3. Method of Solution
3.1. Hybrid Method
- Yeh et al. presented an analogous hybrid approach and proposed the localized functional
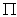 based on Mei’s boundary value problem as
based on Mei’s boundary value problem as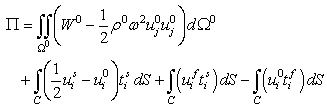 | (1) |
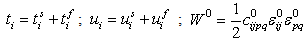 | (2) |
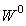 is the strain energy density function and the superscripts s and f are denoted as scattered and free fields, respectively. Since
is the strain energy density function and the superscripts s and f are denoted as scattered and free fields, respectively. Since 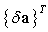 and
and 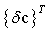 are arbitrary, the following matrix equation is obtained.
are arbitrary, the following matrix equation is obtained.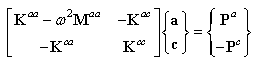 | (3) |
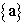 . Therefore, the displacement in
. Therefore, the displacement in 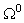 is
is 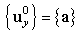 | (4) |
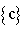 . The displacement in
. The displacement in 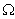 is shown as
is shown as | (5) |
3.2. Transfinite Interpolation
- The hybrid method includes finite element method and series expansion. To combine these two methods, some skill is needed in calculation. For example, the auxiliary boundary C must be semi-circular curve, and the nodal numbers along C must be the last. So, it is not easy to use the conventional finite element method to mesh grids. Therefore, the transfinite interpolation function is introduced in this study. The arbitrary finite domain
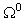 is mapped into a rectangular domain
is mapped into a rectangular domain 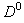 and its finite element meshes are discretized in the rectangular domain. The domain
and its finite element meshes are discretized in the rectangular domain. The domain 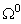 is called the physical region, and the domain
is called the physical region, and the domain 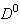 is called the logical region, as shown in Fig. 1 (a) and (b), respectively.
is called the logical region, as shown in Fig. 1 (a) and (b), respectively.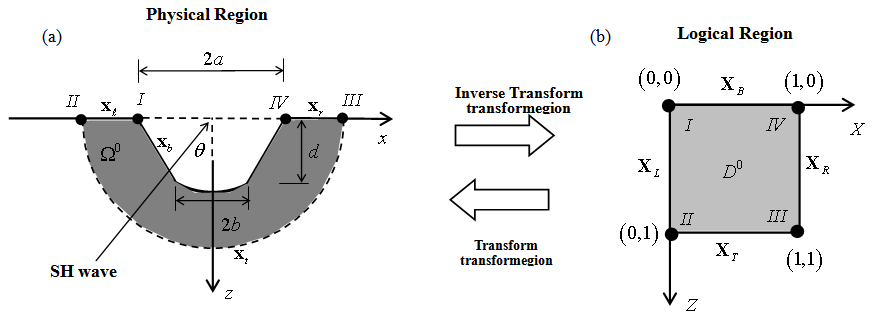 | Figure 1. Schematic diagram illustrating (a) physical region and (b) logical region |
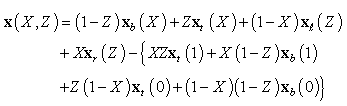 | (6) |
 and
and  Figure 1(a) plots
Figure 1(a) plots 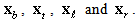 If the shape of the surface irregularity is known, then the coordinates of
If the shape of the surface irregularity is known, then the coordinates of 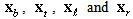 are given. Then, Eq. (6) is used to eliminate the coordinates of the mesh grids in the physical region
are given. Then, Eq. (6) is used to eliminate the coordinates of the mesh grids in the physical region 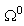 . The merit of TFI is that the flexibility of finite elements favors the modeling of the surface irregularity.
. The merit of TFI is that the flexibility of finite elements favors the modeling of the surface irregularity.3.3. Numerical Verification of the Hybrid Method Combined with TFI
- The cases of a sloping U-shaped canyon with top width 2a, bottom width 2b and depth d are simulated to validate the hybrid method. For the case depth parameter
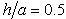 is a deep sloping U-shaped canyon, and
is a deep sloping U-shaped canyon, and 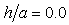 is a shallow sloping U-shaped canyon. In this study, 576 Q8 elements and 1825 nodes are used to mesh the domain
is a shallow sloping U-shaped canyon. In this study, 576 Q8 elements and 1825 nodes are used to mesh the domain  Figure 2 presents the mesh distributions on a deep sloping U-shaped canyon (
Figure 2 presents the mesh distributions on a deep sloping U-shaped canyon (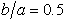 and
and 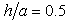 ) and a shallow sloping U-shaped canyon (
) and a shallow sloping U-shaped canyon (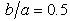 and
and 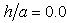 ) in 2 cases. The canyon is impinged upon by incident SH waves with dimensionless frequency
) in 2 cases. The canyon is impinged upon by incident SH waves with dimensionless frequency 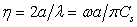 which is the ratio of the width of the sloping U-shaped canyon to the incident wave length
which is the ratio of the width of the sloping U-shaped canyon to the incident wave length 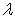 of the half-plane shear wave. Notably, the free field amplitude of displacement on the half-plane surface equals two and is independent of the incident angle
of the half-plane shear wave. Notably, the free field amplitude of displacement on the half-plane surface equals two and is independent of the incident angle 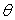 and
and 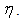
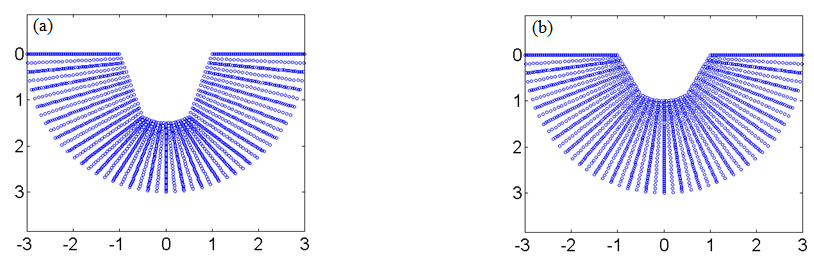 | Figure 2. Mesh grid for a (a) a sloping U-shaped canyon with 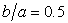 and and 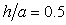 (b) a sloping U-shaped canyon with (b) a sloping U-shaped canyon with 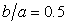 and and 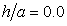 |
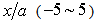 and
and 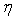 (0.1 to 2.0) for four incident angles
(0.1 to 2.0) for four incident angles 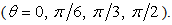 Since the input is a harmonic SH wave of unit amplitude, the total displacements of the region are transfer functions. It is useful in separating out the topographic effects when we attempt to determine the input motion to find source parameters. Consequently the application is based on transfer functions.
Since the input is a harmonic SH wave of unit amplitude, the total displacements of the region are transfer functions. It is useful in separating out the topographic effects when we attempt to determine the input motion to find source parameters. Consequently the application is based on transfer functions.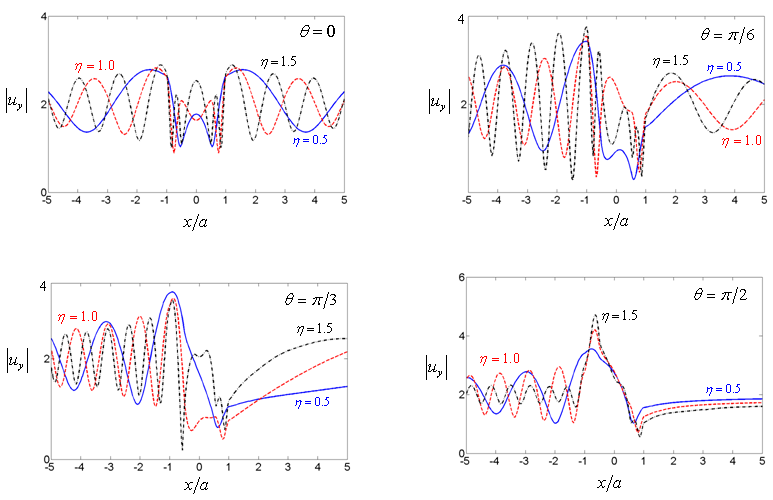 | Figure 3. Amplitude of surface displacement of a sloping U-shaped canyon with 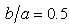 and and 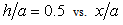 and η and η |
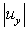 with
with 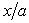 at
at 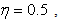 1.0 and 1.5 at
1.0 and 1.5 at 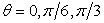 and
and  respectively. In Ref. [15], the corner effect of the canyon and the canyon-decayed effect are described for site effect of canyon. For example the large amplitudes occurred at the corner closed to the wave source as the corner effect, and the displacement amplitudes decay along the canyon as the canyon-decayed effect. The characteristics are observed in the results for sloping U-typed canyon.
respectively. In Ref. [15], the corner effect of the canyon and the canyon-decayed effect are described for site effect of canyon. For example the large amplitudes occurred at the corner closed to the wave source as the corner effect, and the displacement amplitudes decay along the canyon as the canyon-decayed effect. The characteristics are observed in the results for sloping U-typed canyon.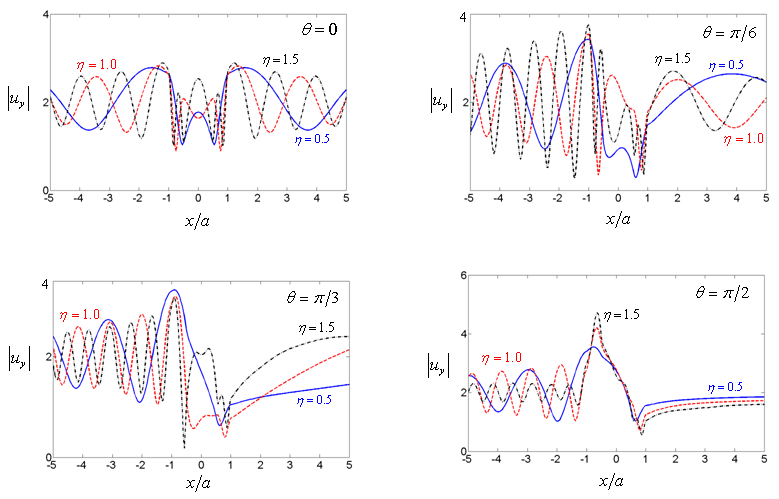 | Figure 4. Amplitude of surface displacement of a sloping U-shaped canyon with  and and 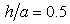 vs. vs. 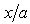 and and 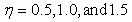 at at 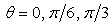 and and 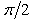 |
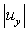 of shallow sloping U-shaped canyon (blue solid line) and trapezoid canyon [14] (red dash line) with
of shallow sloping U-shaped canyon (blue solid line) and trapezoid canyon [14] (red dash line) with 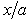 at
at 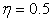 and 1.5 at
and 1.5 at 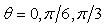 and
and 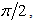 respectively. The width of the top, bottom and depth of the two canyons are the same, the only difference between the two canyons is the bottom shape. It is clearly shown that the displacement amplitudes
respectively. The width of the top, bottom and depth of the two canyons are the same, the only difference between the two canyons is the bottom shape. It is clearly shown that the displacement amplitudes 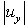 almost similar for low frequency
almost similar for low frequency 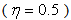 with four incident angles, however the displacements along the bottom canyon are changed due to the curve. For high frequency
with four incident angles, however the displacements along the bottom canyon are changed due to the curve. For high frequency  the displacements show more differences, however, the changes still limit at the bottom of the canyon. It shows the results of sloping U-shaped canyon are smoother cause the bottom shape of the canyon is also smooth. The results also show that, the displacements along the canyon surface change due to the very little change of the canyon shape.
the displacements show more differences, however, the changes still limit at the bottom of the canyon. It shows the results of sloping U-shaped canyon are smoother cause the bottom shape of the canyon is also smooth. The results also show that, the displacements along the canyon surface change due to the very little change of the canyon shape.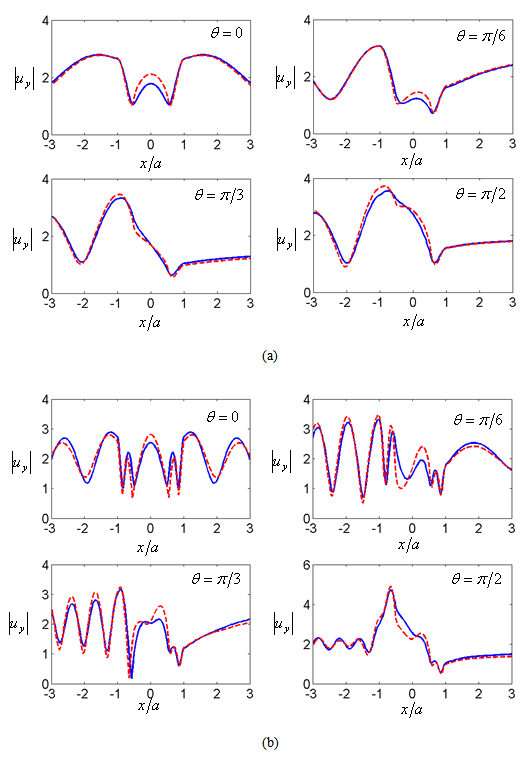 | Figure 5. Amplitude of surface displacement of a sloping U-shaped canyon with  and and  (blue solid line) and trapezoid canyon [] (red dash line) for incident SH wave with (a) (blue solid line) and trapezoid canyon [] (red dash line) for incident SH wave with (a) 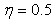 and (b) and (b) 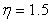 at at 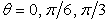 and and 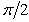 |
4. Conclusions
- A hybrid method based on series solutions combined with finite element method is introduced to solve the SH waves scattering induced by a sloping U-shaped canyon. The mapping function TFI is used to mesh to area included the irregularity. It is comfortable and easy to establish the grids for finite elements. When the canyon is reduced closed to a trapezoid canyon, the surface displacements are compared with the results of trapezoid canyon, and the differences are shown in results. It shows the advantage of hybrid method to solve the scattering problem induced by surface irregularity.For the results of this study, it also shows the merit of hybrid method to solve the scattering problems for complicated topographies. The other advantage of the hybrid method, in which the basis functions satisfy the conditions of the in-plane problem, is that it can be used to solve the problem of the scattering of in-plane P-, SV-, or Rayleigh incident waves.
ACKNOWLEDGEMENTS
- The author would like to thank the National Science Council, Taiwan, R.O.C. for financially supporting this research under Contract No. NSC 102-2221-E-020-011-.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML