1. Introduction

Early detection of defects in civil structures is a critical process in assisting structural maintenance and management plans. With a robust damage detection methodology, it becomes possible to fix the structure during the early stages of damage, therefore, avoiding any future unanticipated accidents that may result in physical, economical, and psychological effects on the society.

Frequency domain methods rely on analytical models but time domain methods are independent of modal parameters and analytical models. Zang et al. [1] presented a structural damage detection method combining independent component analysis extraction of time domain data and artificial neural network to reduce measurement noise. Lu and Gao [2] proposed a time-series model for structural damage considering a damage sensitive feature and unknown input excitation. Nguyen et al. [3] presented some applications of a principal component analysis from output-only measurements in the time and frequency domain for damage detection.

Most damage detection methods are performed utilizing the data in the frequency and time domain. The accuracy of the damage detection methods depends on the sensitivity to external noise. Thus, it is practical to import the damage detection method to diminish the noise effect. This study starts with the displacement responses measured or simulated in the time domain. The data transformed to the ones in the frequency and time domain. The estimated curvature using the transformed data is utilized as the damage index. The applicability of the proposed methods is investigated and compared through a numerical experiment.

2. Time and Frequency Domain Approach for Damage Detection

The dynamic response of a structure of n dofs in the time-domain which is assumed to be linear and subjected to random base excitation can be described by the equations of motion

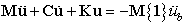(1)

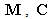where and 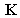denote the 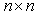analytical mass, damping, and stiffness matrices, respectively, 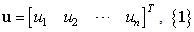, is a vector with all its elements equal to 1, and 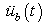is the unknown acceleration of base excitation.

Dynamic responses of practical system are contaminated by external noise. In this study, the noise is simulated by adding a series of random numbers to the calculated displacement responses. The displacements 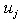for describing the practical responses at node j can be calculated from the simulated noise-free displacements, 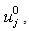by the following equation:

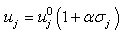(2)

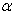where denotes the relative magnitude of the error and 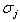is a random number variant in the range

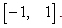The simulated displacements in the time domain contaminated by external noise should be utilized as basic data in detecting damage. However, the displacement responses do not provide accurate information on the damage and should be transformed to the data in the frequency and time domain. And the results are compared according to the applicability of the damage detection method.

The displacements in the time domain are transformed to the ones in the frequency domain by taking fast Fourier transform (FFT). Taking the maximum values of absolute amplitude corresponding to the first resonance frequency at all nodes and estimating their curvature using a central difference method, the damage is traced.

As the other approach, the displacements within a certain range of the time domain are transformed to the proper orthogonal mode (POM). The proper orthogonal decomposition (POD) of a discrete field involves solving the eigenvalue problem. Let 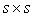matrix 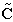be defined as

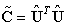(3)

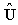where denotes the displacement response matrix in the time domain extracted to obtain the POMs,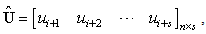 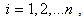and s is the number of the displacement response data sets extracted after the first r frequency response function (FRF) data sets. Solving the eigenvalue problem of Eq. (5) at the core of the POD method, Eq. (5) satisfies

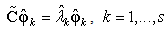(4)

where the eigenvalues are arranged as follows:

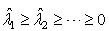(5)

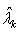where the eigenvalues are the proper orthogonal values (POVs) and each eigenvector 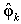of the extreme value problem is associated with a POV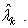 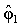represents the eigenvector corresponding to the largest eigenvalue

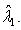The POMs may be used as a basis for the decomposition of 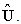The POM associated with the greatest POV is the optimal vector. If the eigenvalues are normalized to unit magnitude, they represent the relative energy captured by the corresponding POM. The eigenvalue reflects the relative kinetic energy associated with the corresponding mode. The energy is defined as the sum of the POVs. The POMs are written as

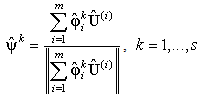(6)

The POMs are arranged as follows:

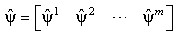(7)

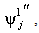This work utilizes the curvature of the POM corresponding to the first POV which is the optimal vector as the damage index to predict the damage occurrence. The curvature at each location j corresponding to the first POV on the structure, is numerically obtained by a central difference approximation:

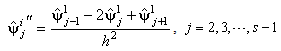(8)

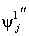where is the second derivatives at the jth node of the first POM and the h is the distance between two successive nodes.

In the following, the validity of the proposed methods in the frequency and time domain is investigated is illustrated in a numerical experiment. And the applicability of the methods is compared based on the results of the tests.

3. Numerical Experiment

A numerical experiment was performed in detecting damage of a finite element model of a fixed-end beam shown in Fig. 1 to examine the validity of the proposed method. The nodal points and the elements are numbered as shown in the figure. A beam with a length of 1 m is modeled using 50 beam elements. The beam has an elastic modulus of 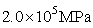and a unit mass of 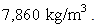The beam’s gross cross section is 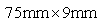and its damage section is established as 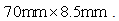The damping matrix is assumed as a Rayleigh damping to be expressed by the stiffness matrix and a proportional constant of 0.0001. This application considers the damage detection of beam structure with multiple damages at elements 15 and 38.

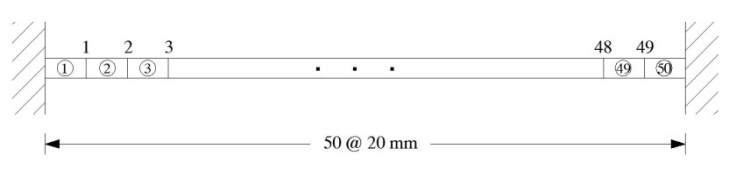Figure 1. A fixed-end beam structure model

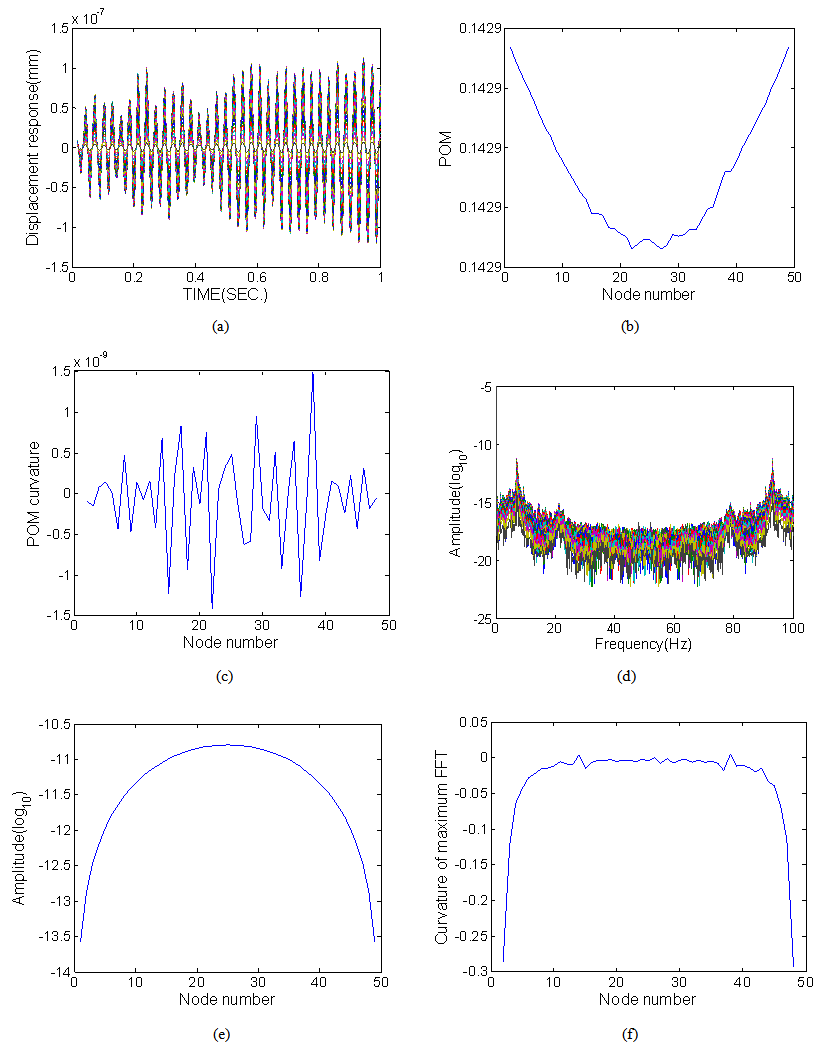
Assume the beam structure is subjected to the very low excitation at the left support with a step size of shown in Fig. 2. The displacement responses in the time domain are calculated by solving the dynamic equation of the finite element model. The measured displacement responses including contaminated external noise are described by inserting in Eq. (2).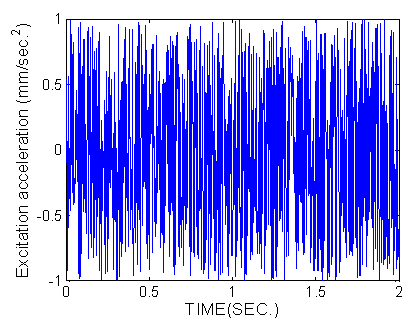

Figure 2. Accelerations of external excitation at the left support

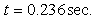Figure 3(a) represents the displacement responses at all nodes during the first one second due to very low excitation at the left support. The displacement responses include 3% external noise. Extracting the displacement data sets between and 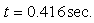, the POM corresponding to the first POV and its curvature are obtained in Figs. 3(b) and (c), respectively. The damage is detected by the abrupt change in the POM curvature curve. It is shown that the damage locations do not correspond with the positions of the abrupt change. It indicates that the curves are sensitive to the external noise and do not provide the accurate clue of the damage.

Figure 3. Numerical results: (a) displacement responses, (b) POM curve extracted from displacement responses, (c) its curvature, (d) FFT curve, (e) curve by the maximum FFT in the neighborhood of the first resonance frequency, (f) its curvature

The previous example alludes that the displacement responses in the frequency domain can be utilized in detecting damage. Transforming the displacements in the time domain to the ones in the frequency domain by FFT, the absolute amplitude curve in logarithmic unit is shown in Fig. 3(d). And taking the maximum values at all nodes in the first resonance frequency 7Hz, the resulting curve is exhibited in Fig. 3(e) and its curvature estimated by a central difference method is shown in Fig. 3(f). The plots are rough and uneven due to the mixed effect of the noise and damage. Comparing with uneven degree along the curvature curve, it is found that the positions of more abrupt change correspond with the damage locations. From the numerical examples, the data transformed to the frequency domain rather than the time domain can be more usefully utilized in detecting damage despite the existence of external noise.

4. Conclusions

Most damage detection methods are affected by external noise. This work considered the damage detection to diminish the noise effect. performed utilizing the data in the frequency and time domain. Starting with the displacement responses in the time domain, the data are transformed to the ones in the frequency and time domain. Estimating the curvature of the transformed data, a damage detection method was presented and its validity and comparison were illustrated in a numerical experiment.

ACKNOWLEDGEMENTS

This research is supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2013R1A1A2057431).