-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2013; 3(1): 22-34
doi:10.5923/j.jce.20130301.03
Natural Frequencies of Seiche in a Closed Trapezoidal Basin with Internal Barriers
A. R. Kabiri-Samani
Department of Civil Engineering, Isfahan University of Technology, Isfahan, Iran
Correspondence to: A. R. Kabiri-Samani , Department of Civil Engineering, Isfahan University of Technology, Isfahan, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A seiche is the free oscillation of water in a closed or semi-closed basin; it is frequently observed in harbors, bays and lakes. Enclosed basins can experience oscillations due to a variety of causes. The enclosed basin has certain natural frequencies of seiche, depending on the geometry of the water boundaries and the bathymetry of water depths. Therefore, the variation in water surface at a point becomes irregular as caused by the combination of several natural frequencies, which may be considered as the superposition of sinusoidal frequency components of different amplitude. This paper is mainly concerned with the motion of an incompressible irrotational fluid in a closed trapezoidal basin with internal impervious barriers. An analytical solution is presented for predicting the characteristic of generated waves in these types of basins. The equations of free water surface oscillations and its boundary conditions are reduced to a system of linear equations, which is solved by applying the small amplitude water wave theory. The flow potential, wave amplitude, flow patterns, and the natural period of waves generated in the basin with impervious internal barriers are found based on the basin geometry. It is shown that the natural period of basin is strongly dependent to the location of barriers and the size of barrier’s opening.
Keywords: Waves, Seiche, Water Surface Free Oscillation, Natural Frequences, Analytical Model
Cite this paper: A. R. Kabiri-Samani , Natural Frequencies of Seiche in a Closed Trapezoidal Basin with Internal Barriers, Journal of Civil Engineering Research, Vol. 3 No. 1, 2013, pp. 22-34. doi: 10.5923/j.jce.20130301.03.
Article Outline
1. Introduction
- Standing waves in natural basins are called seiches. Seiches can be generated by tectonic movements or winds. Like water sloshing in a bathtub, seiches are tide-like rises and drops in great lakes coastal water levels caused by prolonged strong winds that push water toward one side of the lake, causing the water level to rise on the downwind side of the lake and to drop on the upwind side. When the wind stops, the water sloshes back and forth, with the near-shore water level rising and falling in decreasingly small amounts on both sides of the lake until it reaches equilibrium. They occur commonly in enclosed or partially enclosed basins and are usually the result of a sudden change or a series of intermittent-periodic changes in atmospheric pressure or wind velocity. The period of oscillation of a seiche depends on the causative force, which sets the water basin in motion and the natural or free oscillating period of the basin (Figure 1). Seiches can inflict damage, if the natural period of a moored ship matches that of a seiche, then considerable motion will result in the moored ship. Seiches could damage structures along the coastline, and create large vertical accelerations for offshore structures such as boats, barges and floating piers. Shoreline flooding may be caused by storm surges or seiches, often occurring simultaneously with high waves. The appearance of these seiches can be simulated by tilting a basin partially filled with water and then setting it down on a level surface. The water will slosh back and forth at a period determined by the size and shape of the basin. If the natural period, or seiche period, is close to the period of one of the tidal species, the constituents of that species will be amplified by resonance more than those of other species. A variety of seiche periods may appear in the same water level record because the main body of water may oscillate longitudinally or laterally at different periods. The various modes of seiching correspond to the natural frequency response of the water body. There are an infinite number of seiching modes possible, from the lowest (mode 1) to infinity. Realistically, the lower modes probably occur in nature, as frictional damping affects the higher modes preferentially. If the rectangular basin has significant width as well as length, both horizontal dimensions affect the natural period, given by Ippen[1] as:
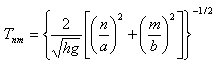 | (1) |
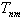 is the natural free oscillation period, n, and m are the modes of oscillation in longitudinal and lateral coordinates respectively and a, and b are the length and width of the rectangular basin. However, the most studied is harbour oscillations caused by incident waves, which have typical periods of a few minutes. Due to strong wind or long wave energy, the water body of a harbor exhibits oscillatory resonant motions. A number of theoretical and numerical investigations of such resonant oscillations have been carried out, but most of them were limited to harbors with constant depth connected with open sea. The free oscillation in closed rectangular and circular basins was analyzed by Lamb[2]. These solutions clarified the natural periods and modes of free surface oscillations related to these special configurations. Neumann[3] focused on the global seiche modes of the entire Baltic, using sea-level data from a number of events when particularly pronounced standing oscillations. His theoretical analysis is based on computational methods presented by[4]. The forced oscillation in a circular harbour connected to the open sea through a narrow mouth was studied by[5]. Since the radiation effect was ruled out, the results showed a harbor resonance as it does in a closed basin. An analytical model for the oscillations of water in a bay or lake, using an electronic network and an electric analogue computer was developed by Ishiguro[6]. Miles and Munk[7], and Ippen and Goda[8], realized that, the open-sea was important in allowing for the loss of energy radiated from a harbor. Iida[9] studied the free oscillation of water in a lake of elliptic boundary. The wave-induced oscillations in harbors of arbitrary shapes was investigated by[10]. The wave induced oscillations of harbors with variable depth was studied by[11]. The free oscillation in a simple two-dimensional closed basin was studied by[1]. The study of harbour resonance has been extended to take into account the effect of bottom friction by[12], wave nonlinearity[13 and 14]. The wave motion and it’s characteristics on a Physical model of small-boat harbour was studied by[15]. Wave-induced oscillation in harbor with porous breakwaters was investigated by[16]. Weakly non-linear long internal wave in closed basin was modelled by[17]. Although the application of numerical models can be used for handling the complexities in this regard, still developing an analytical solution for practical cases can be very useful for parametric study of the free oscillation phenomenon. Kabiri-Samani and Ataie-Ashtiani[18], studied the motion of an incompressible irrotational fluid in a closed rectangular basin with internal impervious barriers based on analytical modeling. They have found new solutions for predicting the characteristic of generated waves in these types of basins, by applying the small amplitude water wave theory. The Lake Urmia is a lake salted in the North-West of the Iran, in the Iranian Azerbaïdjan (between the provinces of Eastern Azerbaïdjan and Western Azerbaïdjan, with the west of the Caspian Sea, which with the same form). It is more the big lake in Iran, with a surface of approximately 5.200 km ². In its greater dimensions, it is approximately 140 km long and 55 km broad. Its maximum depth is approximately 16 m. Urmia lake has a rectangular shape in plan and trapezoidal shape in cross and longitudinal sections (Figure 2). Shahid Kalantari Bridge, is the longest bridge in Iran, which is constructed over Urmia lake and connects Tabriz to Urmia. Due to this natural geometrical properties, construction of Shahid Kalantari Bridge, very similar to internal barriers, over it, there is a potential to perform seiches. This bridge is made of two side rock-filled walls and a bridge deck which is constructed over the opening between the barriers. Due to these similarities to a closed basin with internal barriers, the behavior of free water surface oscillation should be investigated to have informations about the interaction between water surafe free waves and structure.Since this phenomena can cause undesired problems, in this work an analytical solution for calculation of the free water surface oscillations in a trapzoidal basin with internal barriers will be presented. This analytical solution can be applied for the cases such as constructing a causeway in lakes and expansion plan in harbours. The water flow is considered as an ideal and irrotational flow. Therefore the Laplace equation governs to the velocity potential function of flow domain. Free surface boundary condition is linearized to formulate a linear set of equation for solving the small amplitude water wave in the trapezoidal basin. The flow potential, wave amplitude and the natural period of waves generated in the basin with impervious internal barriers are found based on the basin geometry. These parameters are presented for the variations of basin and barriers geometry.
is the natural free oscillation period, n, and m are the modes of oscillation in longitudinal and lateral coordinates respectively and a, and b are the length and width of the rectangular basin. However, the most studied is harbour oscillations caused by incident waves, which have typical periods of a few minutes. Due to strong wind or long wave energy, the water body of a harbor exhibits oscillatory resonant motions. A number of theoretical and numerical investigations of such resonant oscillations have been carried out, but most of them were limited to harbors with constant depth connected with open sea. The free oscillation in closed rectangular and circular basins was analyzed by Lamb[2]. These solutions clarified the natural periods and modes of free surface oscillations related to these special configurations. Neumann[3] focused on the global seiche modes of the entire Baltic, using sea-level data from a number of events when particularly pronounced standing oscillations. His theoretical analysis is based on computational methods presented by[4]. The forced oscillation in a circular harbour connected to the open sea through a narrow mouth was studied by[5]. Since the radiation effect was ruled out, the results showed a harbor resonance as it does in a closed basin. An analytical model for the oscillations of water in a bay or lake, using an electronic network and an electric analogue computer was developed by Ishiguro[6]. Miles and Munk[7], and Ippen and Goda[8], realized that, the open-sea was important in allowing for the loss of energy radiated from a harbor. Iida[9] studied the free oscillation of water in a lake of elliptic boundary. The wave-induced oscillations in harbors of arbitrary shapes was investigated by[10]. The wave induced oscillations of harbors with variable depth was studied by[11]. The free oscillation in a simple two-dimensional closed basin was studied by[1]. The study of harbour resonance has been extended to take into account the effect of bottom friction by[12], wave nonlinearity[13 and 14]. The wave motion and it’s characteristics on a Physical model of small-boat harbour was studied by[15]. Wave-induced oscillation in harbor with porous breakwaters was investigated by[16]. Weakly non-linear long internal wave in closed basin was modelled by[17]. Although the application of numerical models can be used for handling the complexities in this regard, still developing an analytical solution for practical cases can be very useful for parametric study of the free oscillation phenomenon. Kabiri-Samani and Ataie-Ashtiani[18], studied the motion of an incompressible irrotational fluid in a closed rectangular basin with internal impervious barriers based on analytical modeling. They have found new solutions for predicting the characteristic of generated waves in these types of basins, by applying the small amplitude water wave theory. The Lake Urmia is a lake salted in the North-West of the Iran, in the Iranian Azerbaïdjan (between the provinces of Eastern Azerbaïdjan and Western Azerbaïdjan, with the west of the Caspian Sea, which with the same form). It is more the big lake in Iran, with a surface of approximately 5.200 km ². In its greater dimensions, it is approximately 140 km long and 55 km broad. Its maximum depth is approximately 16 m. Urmia lake has a rectangular shape in plan and trapezoidal shape in cross and longitudinal sections (Figure 2). Shahid Kalantari Bridge, is the longest bridge in Iran, which is constructed over Urmia lake and connects Tabriz to Urmia. Due to this natural geometrical properties, construction of Shahid Kalantari Bridge, very similar to internal barriers, over it, there is a potential to perform seiches. This bridge is made of two side rock-filled walls and a bridge deck which is constructed over the opening between the barriers. Due to these similarities to a closed basin with internal barriers, the behavior of free water surface oscillation should be investigated to have informations about the interaction between water surafe free waves and structure.Since this phenomena can cause undesired problems, in this work an analytical solution for calculation of the free water surface oscillations in a trapzoidal basin with internal barriers will be presented. This analytical solution can be applied for the cases such as constructing a causeway in lakes and expansion plan in harbours. The water flow is considered as an ideal and irrotational flow. Therefore the Laplace equation governs to the velocity potential function of flow domain. Free surface boundary condition is linearized to formulate a linear set of equation for solving the small amplitude water wave in the trapezoidal basin. The flow potential, wave amplitude and the natural period of waves generated in the basin with impervious internal barriers are found based on the basin geometry. These parameters are presented for the variations of basin and barriers geometry.2. Free Oscillations in Closed Basins with Internal Barriers
- Consider the closed trapezedial basin of the bottom width b, length a, constant depth h, and latteral walls slope s, has two internal impervious barriers, which have the length bu and bd and divided the basin to two semi-closed basins as shown in Figure 3. If a periodic motion of the water in this basin is possible, the free oscillation will be described by periods which are function of the basin dimensions.
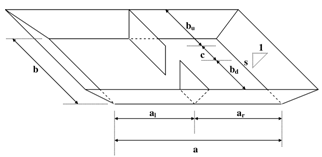 | Figure 3. Three Dimensional closed trapezeidal basin with internal barriers |
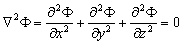 | (2) |
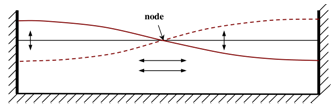 | Figure 1. Schematic standing wave |
 | Figure 2. General plan of Urmia lake |
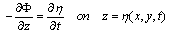 | (3) |
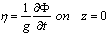 | (4) |
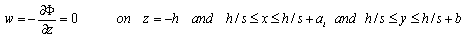 | (5) |
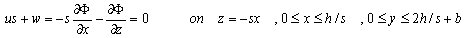 | (6) |
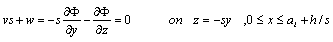 | (7) |
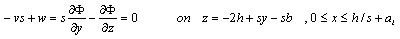 | (8) |
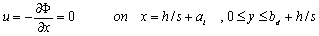 | (9) |
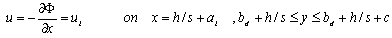 | (10) |
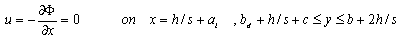 | (11) |
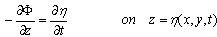 | (12) |
 | (13) |
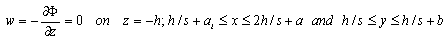 | (14) |
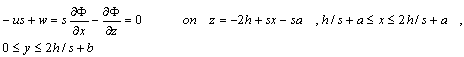 | (15) |
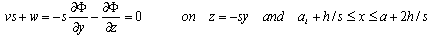 | (16) |
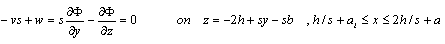 | (17) |
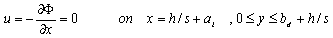 | (18) |
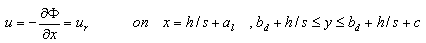 | (19) |
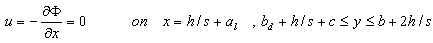 | (20) |
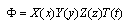 | (21) |
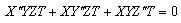 | (22) |
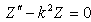 | (23) |
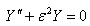 | (24) |
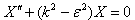 | (25) |
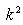 and
and 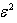 are constants. These equations have the following general solutions
are constants. These equations have the following general solutions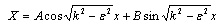 | (26) |
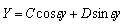 | (27) |
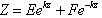 | (28) |
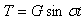 | (29) |
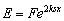 | (30) |
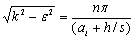 | (31) |
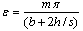 | (32) |
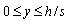
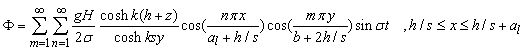 | (33) |
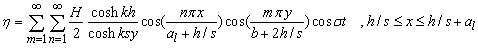 | (34) |
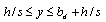
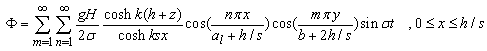 | (35) |
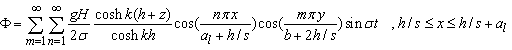 | (53) |
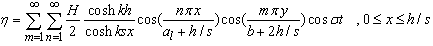 | (36) |
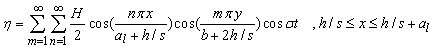 | (37) |
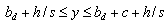 Velocities
Velocities 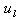 and
and 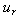 are equal and evaluated by imposing the condition that the wave velocity at
are equal and evaluated by imposing the condition that the wave velocity at 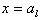 for left semi-closed basin is the same as the wave velocity for right semi-closed basin at this point. hence
for left semi-closed basin is the same as the wave velocity for right semi-closed basin at this point. hence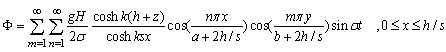 | (38) |
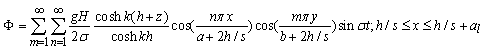 | (39) |
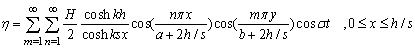 | (40) |
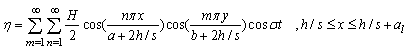 | (41) |
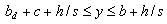 The boundary conditions of this case are the same as those presented for case a therefore
The boundary conditions of this case are the same as those presented for case a therefore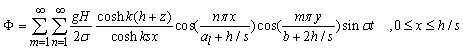 | (42) |
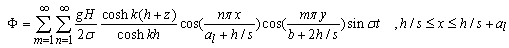 | (43) |
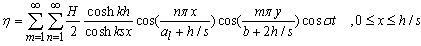 | (44) |
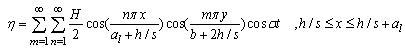 | (45) |
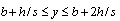
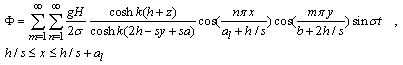 | (46) |
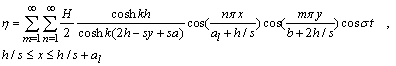 | (47) |
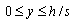
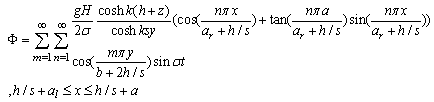 | (48) |
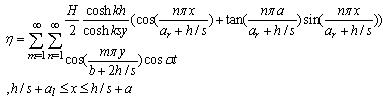 | (49) |
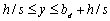
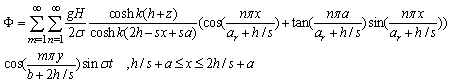 | (50) |
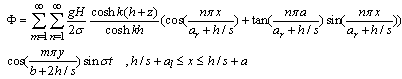 | (51) |
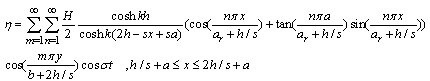 | (52) |
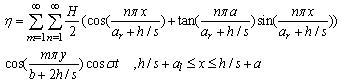 | (53) |
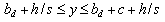 Using the condition of
Using the condition of 
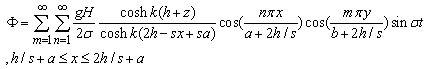 | (54) |
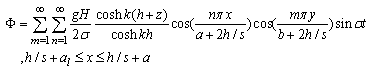 | (55) |
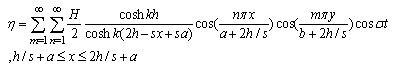 | (56) |
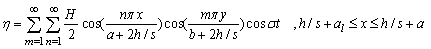 | (57) |
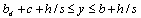 The boundary conditions of this case are the same as those presented for case a therefore
The boundary conditions of this case are the same as those presented for case a therefore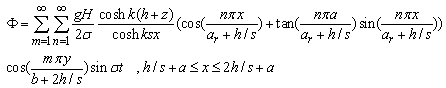 | (58) |
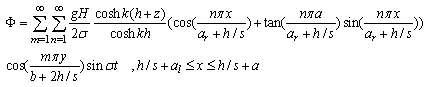 | (59) |
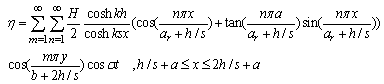 | (60) |
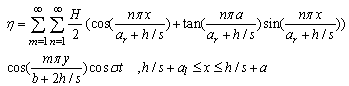 | (61) |
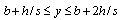
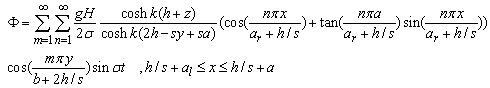 | (62) |
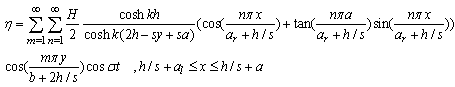 | (63) |
 and
and 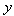 directions, at a closed basin, which is divided into two semi-closed basins, the continuity for shallow water waves results from equating the change in flow in the two directions to the change in storage in the control volume (Figure 4). From Laplace equation and using velocity potential
directions, at a closed basin, which is divided into two semi-closed basins, the continuity for shallow water waves results from equating the change in flow in the two directions to the change in storage in the control volume (Figure 4). From Laplace equation and using velocity potential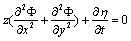 | (64) |
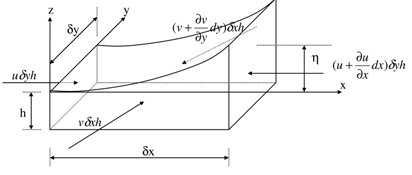 | Figure 4. Selected control volume |
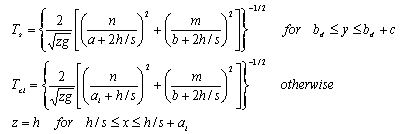 | (65) |
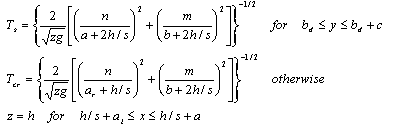 | (66) |
3. Results
- In this section the results of analytical solution presented above for a closed trapezoidal basin with internal barriers are discussed. To check the credibility of the analytical model and it’s out coming results, Figure 6 is presented. Figures 5(a and b) compare the results of present model with the actual data of Geneva lake[19] and lake Lappajarvi[20] respectively. From these figures it can be seen the present analytical model is coincident with the real phenomena and hence could be used as a good tool for preliminary predictions. Figures 6, 7, and 8 show the variation of normalized water level,
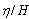 , versus x for various values of al/a and a=25m, b=10m, h/s=2, k=0.5, m=n=1, y=0 and a=25m, b=10m, h/s=2, k=0.5, m=n=1, y=2m and a=25m, b=10m, h/s=5, k=0.5, m=n=1, y=2m respectively. As shown in these figures, the wave length decrease as the ratio of al/a increases. The results are the same as those of a simple closed basin without barriers for limiting conditions as al/a equals 0 and 1. Figure 9 shows the variation of normalized water level,
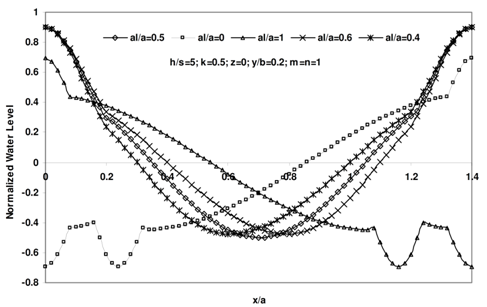
, versus x for various values of al/a and a=25m, b=10m, h/s=2, k=0.5, m=n=1, y=0 and a=25m, b=10m, h/s=2, k=0.5, m=n=1, y=2m and a=25m, b=10m, h/s=5, k=0.5, m=n=1, y=2m respectively. As shown in these figures, the wave length decrease as the ratio of al/a increases. The results are the same as those of a simple closed basin without barriers for limiting conditions as al/a equals 0 and 1. Figure 9 shows the variation of normalized water level, 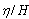 , versus x for various modes of oscillation (m and n) and a/b=2.5, al/a=0.5 h/s=2, k=0.5,and y/b=0.5. As shown in these figures, wave length decrease as the ratio of al/a increases. It can be seen that. the results are the same as those of a simple closed basin without barriers in limiting conditions of al/a equals 0 and 1. The main result of these figures is that, the opening size (c) and the barriers length (bu or bd) have a significant influence on the normalized water level (
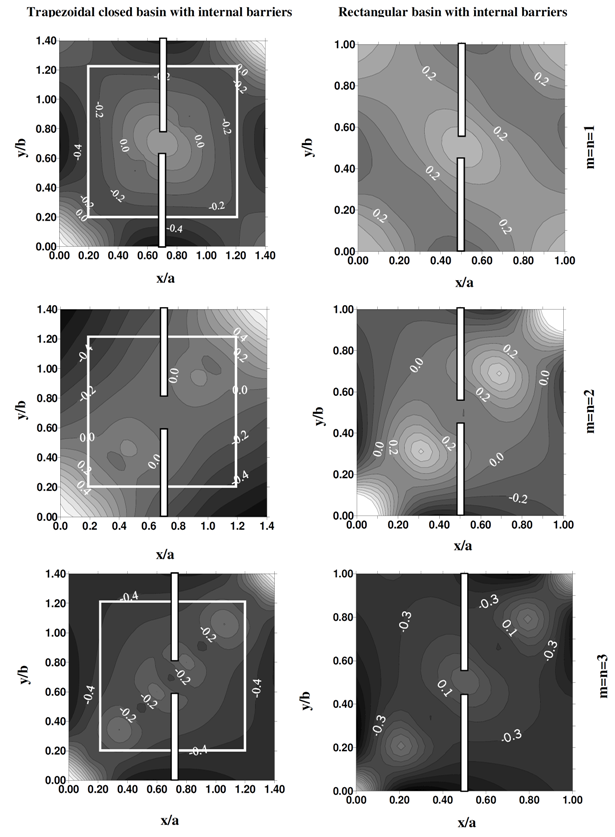
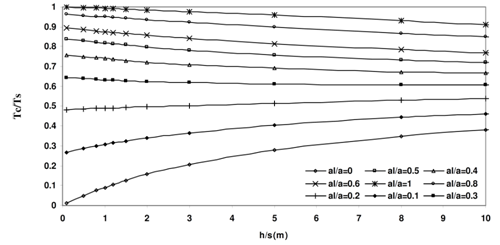
, versus x for various modes of oscillation (m and n) and a/b=2.5, al/a=0.5 h/s=2, k=0.5,and y/b=0.5. As shown in these figures, wave length decrease as the ratio of al/a increases. It can be seen that. the results are the same as those of a simple closed basin without barriers in limiting conditions of al/a equals 0 and 1. The main result of these figures is that, the opening size (c) and the barriers length (bu or bd) have a significant influence on the normalized water level (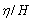 ) at various positions in the basin. Figure 10 shows the normalized water level contours for different modes of oscillation for a rectangular closed basin and trapezoidal closed basin with internal barriers, where, al/a=0.5 and c/b=0.2. These figures illustrate the differences of flow pattern among these two cases. From these figures, the significant influence of internal barriers on flow map, wave-length, and more importantly natural frequency of free oscillation in the basin can be seen.Figure 11 illustrates the normalized natural period Tc/Ts versus h/s for different al/a and m=n=1. From this figure for al/a<0.3 increasing al increase the natural period and for al/a>0.3 increasing al decreases natural period of coupled basin against natural period of simple basin. For large values of h/s the normalized natural period (Tc/Ts) has a limiting value equal to 0.6 for different al/a.
) at various positions in the basin. Figure 10 shows the normalized water level contours for different modes of oscillation for a rectangular closed basin and trapezoidal closed basin with internal barriers, where, al/a=0.5 and c/b=0.2. These figures illustrate the differences of flow pattern among these two cases. From these figures, the significant influence of internal barriers on flow map, wave-length, and more importantly natural frequency of free oscillation in the basin can be seen.Figure 11 illustrates the normalized natural period Tc/Ts versus h/s for different al/a and m=n=1. From this figure for al/a<0.3 increasing al increase the natural period and for al/a>0.3 increasing al decreases natural period of coupled basin against natural period of simple basin. For large values of h/s the normalized natural period (Tc/Ts) has a limiting value equal to 0.6 for different al/a. 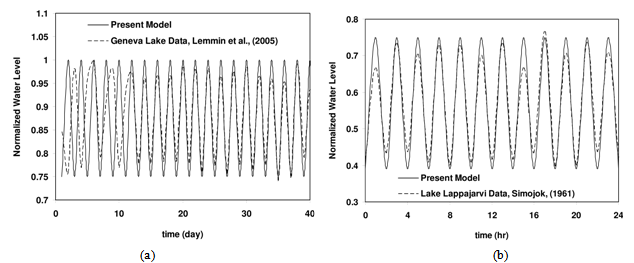 | Figure 5. Comparison between the results of present model with the actual data of (a) Geneva lake (Lemmin et al., 2005) and (b) Lake Lappajarvi (Simojoki, 1961) |
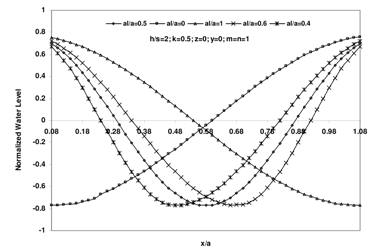 | Figure 6. The variation of normalized water level,  , versus x for a/b=2.5, h/s=2, k=0.5, m=n=1, and y=0 and various values of al/a , versus x for a/b=2.5, h/s=2, k=0.5, m=n=1, and y=0 and various values of al/a |
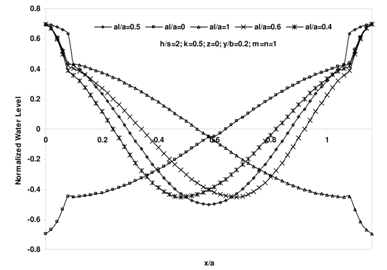 | Figure 7. The variation of normalized water level, 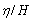 , versus x for a/b=2.5, h/s=2, k=0.5, m=n=1, and y=2m and various values of al/a , versus x for a/b=2.5, h/s=2, k=0.5, m=n=1, and y=2m and various values of al/a |
 | Figure 8. The variation of normalized water level,  , versus x for a/b=2.5, h/s=5, k=0.5, m=n=1, and y=2m and various values of al/a , versus x for a/b=2.5, h/s=5, k=0.5, m=n=1, and y=2m and various values of al/a |
 | Figure 9. Variation of normalized water level, 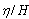 , versus x for various modes of oscillation (m and n) and a/b=2.5, al/a=0.5 h/s=2, k=0.5,and y/b=0.5 , versus x for various modes of oscillation (m and n) and a/b=2.5, al/a=0.5 h/s=2, k=0.5,and y/b=0.5 |
 | Figure 10. Normalized water level contours for different modes of oscillation for a rectangular closed basin and trapezoidal closed basin with internal barriers (al/a=0.5) |
 | Figure 11. The normalized natural period Tc/Ts versus h/s for different al/a |
 | Figure 12. The normalized natural period versus h/s for different modes of oscillation, and al/a=0.5 |
4. Summary
- An analytical solution for the free surface oscillations in a trapezoidal basin with internal barriers was presented. The water flow was considered as an ideal flow. Therefore the Laplace equation governs to the velocity potential function of flow domain. Free surface boundary condition was linearized to formulate a linear set of equation for solving the small amplitude water wave in the trapezoidal basin. The flow potential, wave amplitude and the natural period of waves generated in the basin with impervious internal barriers were found based on the basin geometry. It was shown that the barriers geometry significantly influences the flow map, wave-length, and natural frequency of free water oscillation in the basin. Wave length decrease as the ratio of al/a increases. The opening size, c and the barriers length bu or bd have a significant influence on the normalized water level (
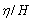 ) at various positions in the basin. The analysis of wave condition dut to the greometrical properties of Urmia lake showed that, the water free suraface osccilation has not undesireable influences on the Urmia lake bridge and it’s breakwaters, due to the sufficient height and free board taken into account for this structure.
) at various positions in the basin. The analysis of wave condition dut to the greometrical properties of Urmia lake showed that, the water free suraface osccilation has not undesireable influences on the Urmia lake bridge and it’s breakwaters, due to the sufficient height and free board taken into account for this structure.NOMENCLATURE
- H wave heightTn natural free oscillation periodT1 the largest periodTcl, Tcr natural period for left and right semi basins respectivelyTs natural period of simple closed basinSn non-dimensional parameter defined as Sl, Sr velocities in x direction at the station of barrier opening for left and right semi basins respectivelyX(x), Y(y), Z(z) functions of x, y, z, and t which, demonstrare flow field or amplitude functionsa, b dimensions of simple closed basinal, ar dimensions of semi basins in x directionbu, bd the size of up and down barriers respectivelyc the opening sizeg gravitational accelerationh water depthk wave numberl length of closed basin along axism , n integers show the oscillation modet timeu, v velocity components at x and y directionsx, y, z cordinatesη water level (amplitude)σ wave frequencyΦ velocity potential function
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML