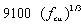-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2012; 2(6): 84-99
doi: 10.5923/j.jce.20120206.05
Reliability Pointers for Modal Parameter Identification of Grandstand Terraces
John N Karadelis
Department of Civil Engineering, Architecture and Building, Coventry University, Coventry, CV1 5FB, UK
Correspondence to: John N Karadelis , Department of Civil Engineering, Architecture and Building, Coventry University, Coventry, CV1 5FB, UK.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The reinforced concrete terrace units were positioned and tested on a specially manufactured steel frame resting on the strong floor in the Civil Engineering laboratories at Coventry University. In parallel, a finite element model was developed and set to free vibration. Natural frequencies and mode shapes were recorded and compared with those obtained experimentally. As correlation was not deemed to be satisfactory, an updating process was initiated and a series of parameters, starting with the concrete material properties were revised to improve links with the experimental results. Boundary conditions built-in the code were not adequate to model the real behaviour of the structure. Best results were achieved when supports conditions were modelled with a stiffness matrix. Correlation between experimental and computer predicted results improved further with the introduction of more advanced modelling techniques and gradual lifting of the limitations of the model, hence assisting the validation process, while verification did not provide the expected degree of confidence. It was concluded that it is possible to extract the natural frequencies and mode shapes of a complex, non-symmetric structure accurately, by using relatively low-cost, basic modal testing equipment and the finite element method of analysis, hence avoiding the risk of not detecting any mode shapes. This can be more apparent in complex modes (e.g. coupled, flexural/torsional) as they depend greatly on the number, position, direction, type and quality of the transducers and data logging and processing equipment used. Emphasis is placed on the experience built up in interpreting modal analysis results in order to be used for similar future work.
Keywords: Modal Analysis, Concrete, Updating, Correlation, Natural Frequencies, Mode Shapes
Cite this paper: John N Karadelis , "Reliability Pointers for Modal Parameter Identification of Grandstand Terraces", Journal of Civil Engineering Research, Vol. 2 No. 6, 2012, pp. 84-99. doi: 10.5923/j.jce.20120206.05.
Article Outline
1. Introduction
- This paper argues that the finite element method can take the leading role in the extraction of modal parameters of civil engineering structures and can help reduce the number of costly, time consuming and complex full-scale modal tests. The confined objectives can be summarised as follows:• To improve modal analysis standards in Civil Engineering by proposing a contemporary system identification method, that effectively captures the natural frequencies and mode shapes of grandstand terraces. • To highlight any inherent uncertainties in numerical simulation by utilizing the processes of experimentation, validation and verification.• To reveal and quantify the most effective parameters affecting the dynamic properties of grandstands.• To comment on the effect of steel reinforcement in the dynamic properties of these structures and identify any inbuilt patterns that may be related to the above.
2. Modal Analysis of Grandstands (Brief Overview)
- The basic assumptions that have to be made to perform an experimental modal analysis of any structure are: • The structure is assumed to be linear, obeying the principle of superposition. • The structure is time invariant, meaning that the parameters to be determined are constant and do not change with time. • The structure obeys Maxwell’s Reciprocity Theorem. Experimental modal identification techniques can be divided into two main categories: Input-Output and Output only and they are almost always accompanied by finite element correlation and updating, hence ensuring that the final output reflects better the measured data.The hybrid (steel skeleton-concrete terraces) method of stadia construction can be susceptible to excessive vibration caused by their users[1],[2],[3]. These vibrations are judged excessive by the discomfort, or even the panic and alarm they can cause to the users (serviceability limit state problem) or in extreme cases, causing low cycle fatigue failure (ultimate limit state problem). The Joint Working Group (JWG) of the Institution of Structural Engineers in UK was established in January 2000 to consider, advise and make recommendations on the dynamic performance and design of stadia structures[4],[5]. The Group completed their work by identifying a number of areas where more research should be directed. One of these areas was the need for accurate numerical modelling of the structures in question[6].More pioneering work has been dedicated to the subject such as publications by Ellis and Littler[7],[8]. Earlier, Ellis and Ji[9], were involved in the estimation of the dynamic properties of structures. They concluded that the experimental study provided realistic but incomplete information while the theoretical study supplied complete but inaccurate results and stressed for more accurate computer simulation. Reynolds et al[10],[11],[12] developed a remote monitoring system to measure the vibration performance of stadia when empty and in-service during sporting and other events. They too, pointed towards the absence of accurate finite element modelling procedures, stressing the need for more accurate, 3D FE modelling to capture the realistic behaviour of the stands. Swan et al[13] established that support conditions are effective in influencing the Frequency Response Function (FRF) measured on a model deck and that the FRF may be used as an accurate general indication of the overall state of stiffness of a bridge’s deck. However, their methodology incorporated elementary support modelling techniques only. Their subsequent consideration of a series of springs created unwanted alignment problems that hindered the process and affected the results. Hence, they were not able to report on the degree of effectiveness and expand on the structure’s stiffness. More recently, Ibrahim and Reynolds[14] demonstrated good correlation of natural frequencies and mode shapes and suggested that progressive modelling of different configurations is a fairly accurate approach in the FE modelling of large structures such as grandstands. It is apparent from the above that accurate and reliable finite element models of large structures, to complement the experimental identification and estimation of their modal parameters are in short supply today. An up to date numerical model and a contemporary modal parameter identification method will be reported in this study emphasizing that some civil engineering structures (grandstands), their boundary conditions and non-structural elements are too large and complex to be modelled at a macro-scale level. Therefore sub-structuring, modelling (and testing) smaller units can show the way to better computer representation of such structures.
3. Full Scale Modal Testing
- Tests were carried out primarily in the Civil Engineering laboratories of Coventry University and to some extent at Bison’s headquarters in Slough, England. The scope of this paper is not to present a detailed account of the experimental programme. This is given elsewhere[15]. However, some essential material is reported here.
3.1. The Vibration Test System
- This is shown in Figure 1. The Shaker is used to deliver the input force. The Amplifier provides power to the shaker’s armature coil. The Signal Generator generates and drives the signal (sine, square, ramp, even earthquake simulations) to the shaker. The Spectrum (FFT) Analyser, performs time and frequency domain analysis, calculates the frequency response function (FRF) and exports all data to a personal computer. Finally, the accelerometers (barely visible here) trace the structure’s response.
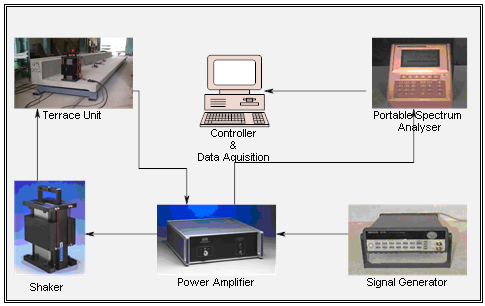 | Figure 1. Modal Analysis Data Acquisition Test System |
3.2. The Test Programme
- The objective was to take measured data relating to the response properties (such as the input frequency) of a structure and from these to extract the modal properties (natural frequencies, etc). The terrace unit was modelled by dividing it into a set of lumped masses shown in Figure 2. In modal analysis, masses are used as data collection (reference) points (RPs) and the properties of the structure are determined by measuring the FRF (Frequency Response Function) at each of the RPs. The response of the unit was measured at two locations, RP3 and RP5. To ensure linearity, samples of the amplitudes reached during the tests were compared with the allowable static deflections and found to be well within range.
 | Figure 2. A terrace unit in the laboratory and its corresponding modal test grid |
 < 0.05). In the case of hybrid (steel-concrete) grandstands the damping present is even less. As
< 0.05). In the case of hybrid (steel-concrete) grandstands the damping present is even less. As  is small, the damped natural frequency becomes approximately equal to the natural frequency
is small, the damped natural frequency becomes approximately equal to the natural frequency  at near resonance conditions. Hence, the error involved by neglecting the damping effects in a modal analysis of a large structure is negligible. Therefore, the damping effects were omitted from the assessment of the structure.
at near resonance conditions. Hence, the error involved by neglecting the damping effects in a modal analysis of a large structure is negligible. Therefore, the damping effects were omitted from the assessment of the structure.4. An Analytical Outline
- In the case of the terrace units having no plane of symmetry, the problem becomes significantly more complex and involves coupled torsional and flexural vibrations in the two principal planes. Weaver et al[17] warned of the development of three simultaneous differential equations instead of two and radically more elaborate analysis and computations. The entire, detailed analytical model is presented elsewhere[18] but an insight is outlined below, based on Figure 5.
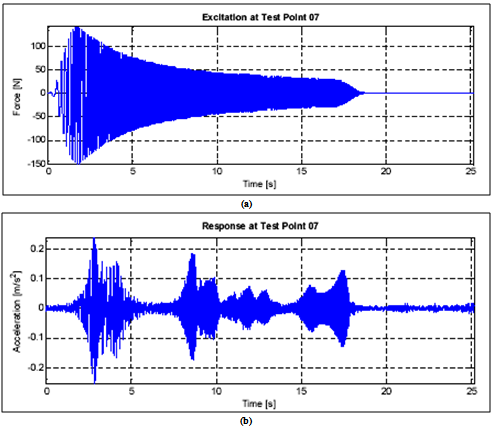 | Figure 3. Typical excitation (a) and response (b) signals of the unit |
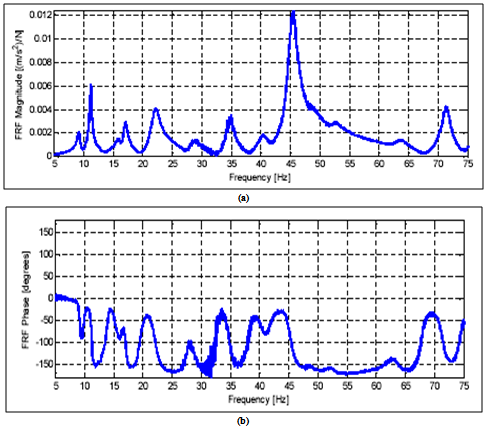 | Figure 4. Typical FRF at RP7, after four averages (a): FRF peaks. (b): their characteristic phase changes |
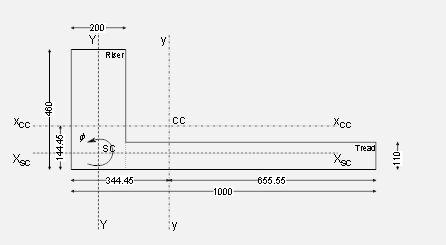 | Figure 5. Cross-section of a terrace unit. CC = centroid, SC = shear centre. All dimensions in mm |
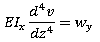 | (1) |
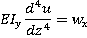 | (2) |
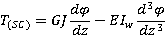 | (3) |
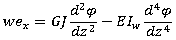 | (4) |
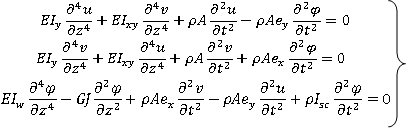 | (5) |
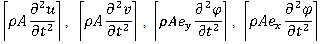 denote mass and inertia associated with linear and angular acceleration respectively,
denote mass and inertia associated with linear and angular acceleration respectively,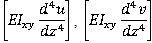 indicate coupling effects,
indicate coupling effects,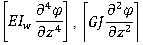 are the warping and torsional terms respectively,
are the warping and torsional terms respectively,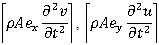 represent inertia forces and
represent inertia forces and 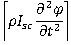 represents inertial torque.After processing the EoM, the boundary conditions are introduced (z= 0 and z= ℓ) and the Frequency Equation can be structured by setting the determinant of Eqs. (5) equal to zero ((5)= 0). Following a vast amount of mathematical computations not shown here, the final Frequency Equation with respect to yields:
represents inertial torque.After processing the EoM, the boundary conditions are introduced (z= 0 and z= ℓ) and the Frequency Equation can be structured by setting the determinant of Eqs. (5) equal to zero ((5)= 0). Following a vast amount of mathematical computations not shown here, the final Frequency Equation with respect to yields: 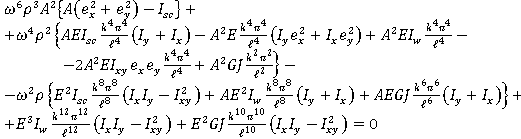 | (6) |
5. Numerical Modal Analysis
- In general, it is assumed that the structure has constant stiffness and mass effects and that there is no damping present for reasons discussed earlier. No constant or time dependent forces or displacements are applied (free vibration). Hence, the eigenvectors are the displacement solutions of the equilibrium equation of motion for free, undamped vibrations:
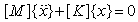 | (7) |
 | (8) |
 = vector of order n (amplitude)
= vector of order n (amplitude)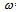 = natural circular frequency of vibrationEquation (9) shows the classic eigenvalue problem used in a typical undamped modal analysis.
= natural circular frequency of vibrationEquation (9) shows the classic eigenvalue problem used in a typical undamped modal analysis.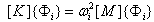 | (9) |
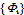 = mode (shape) vector (eigenvector) of mode i
= mode (shape) vector (eigenvector) of mode i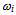 = natural circular frequency of mode
= natural circular frequency of mode 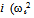 is the eigenvalue)It can be shown easily that:
is the eigenvalue)It can be shown easily that: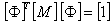 | (10) |
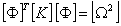 | (11) |
5.1. The Initial, ‘Static’ Model
- The initial, static numerical model used in this study has been published elsewhere[19],[20]. However, essential matter such as a brief account of the model built-up, material and geometric properties, boundary conditions, etc, particularly in conjunction with the process of correlation, will be reported here to aid the reader. Also, the method of extracting the mode shapes is of interest and will be briefly addressed. The terrace units (Figure 2) were designed, manufactured and transported to the laboratory by Bison Concrete Products Ltd. They were designated uncracked upon delivery. Table 2 summarises the basic properties. The Modulus of Elasticity of concrete was taken from relationships and tests shown condensed in Table 3. The Modulus of Elasticity of high yield steel reinforcement and its 0.2% proof stress were estimated by routine laboratory tests[19].
| |||||||||||||||||||||||||||
|
|
5.2. Updating Strategy, Correlation, Fine-tuning, Validation
- The goal of FE model updating is to achieve an improved match between model and test data by making meaningful changes to model parameters and rectify any inaccurate modelling assumptions. Updating methods are based primarily on the sensitivity of selected physical parameters, so that correlation between simulated responses and target values improves. Figure 6 summarizes the updating strategy in a symbolic flow-chart for Terrace Unit Member 003 (TUM003). The main difference between computational and manual updating is that the former allows for a simultaneous variation of more than one parameter and therefore should be a good deal faster. However, the choice of appropriate model parameters can be an obscurity as they do not always deliver reliable results. The response can be correlation values like MAC (Modal Assurance Criterion), the most popular criterion for correlating vectors in a computer driven FE model updating. The purpose of a successfully updated FE model is to be used for further structural analysis, or model other load and boundary conditions, or even different configurations (such as damage) with much more confidence and without additional experimental testing.
5.3. Gradual Updating and Correlation
- A plain concrete model taken from a previous static analysis of the same terrace units and with the material properties shown in Table 5 was used as an opening case. The results predicted are shown compared with those collected from tests. The percentage error is also shown but it is based on the experimental (measured) values which can only be assumed to be accurate. The fact that all accelerometers were positioned vertically on the structure and therefore not make up for other directions may account for that. A more realistic indicator, such as the percentage deviation from the arithmetic mean of the two values is also shown. This may be more erroneous than the percentage error at the beginning of the updating process but should become more accurate at a later stage when correlation improves. A first attempt to correlate the measured and predicted results is plotted in Figure 7.
 | Figure 6. The updating process summarised |
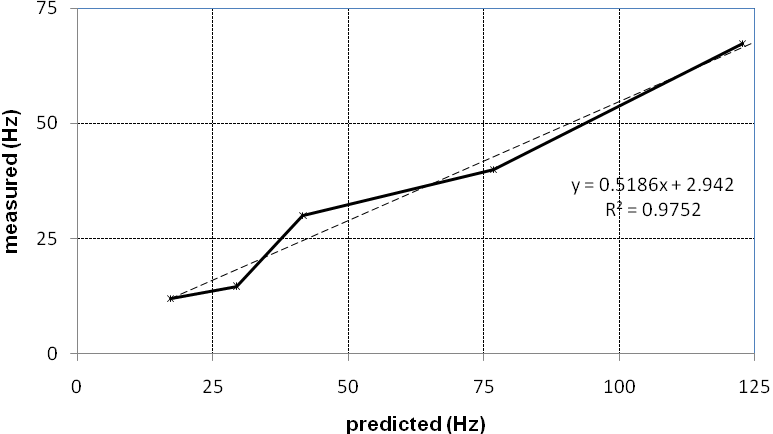 | Figure 7. Preliminary correlation between measured and predicted natural frequencies |
5.4. Initial FE Model
- As expected, the composition of the first finite element model is not satisfactory; hence the updating process. However, sometimes it is possible that the final parameter changes do not allow for a physical interpretation. They are simply numerical substitutes accountable for reducing the deviations between tests and FE analysis. Whether the latter are physically acceptable or not depends a great deal on the field of application of the model. For example, a large, disproportionate increase in the thickness of shell elements may be unacceptable for a static stress analysis but has no effect on modal analysis. Hence, in a manually updating process it is left to the analyst to decide and justify whether the resulting model is acceptable and realistic or not. The slope of the ‘best-fit’ was chosen as a correlation index. The initial slope was 0.518. This is, out by 0.482, or 48.2%, from a perfect correlation (target), taken as one.
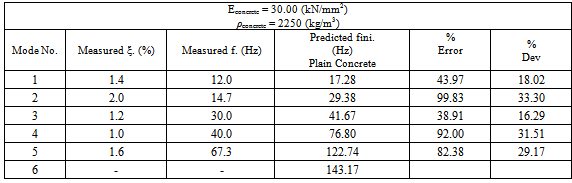
5.5. First Update (Material Properties)
- It has been said that finite element analysis overestimates stiffness[23],[24],[25]. This is usually attributed to overestimation of material properties, the variation of stiffness in different directions and interaction problems between two neighbouring materials, as it is shown later. Hence, as stiffness is directly related to the square of the natural frequency, it is expected that FE Analysis will overestimate the natural frequencies. The first update was based on the variation of material parameters. Hence, the inserted value for Young’s Modulus of concrete was lowered and the corresponding value for density was raised in an effort to come near the measured natural frequencies. Both variations were performed within the acceptable boundaries of the parameters themselves. Table 6 and Figure 8 display the details and the results.The results show a noticeable improvement in the predicted variables and a reduction in the percentage error and percentage deviation compared with the initial model. The slope of the ‘best fit’ curve has been improved from 0.518 to 0.705; an upgrading of 0.187 towards the target value, or 0.295 (29.5%) away from unity. The largest deviation occurred at mode 4 and the smallest at mode 1, as expected.
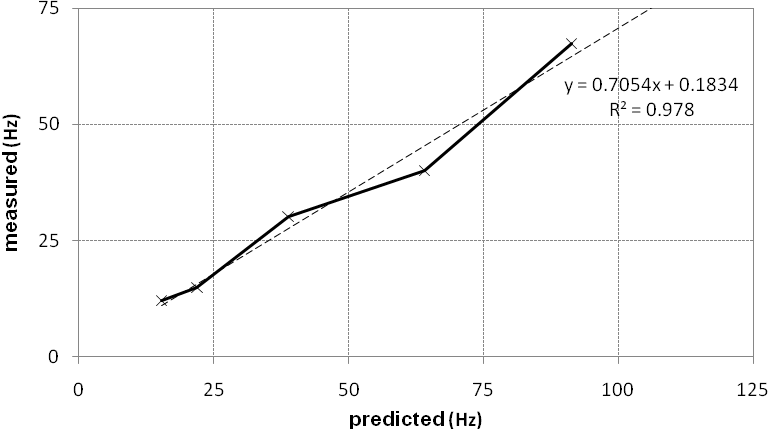 | Figure 8. First correlation between measured and predicted natural frequencies |
|
|
|
5.6. Second Update (Reinforcement)
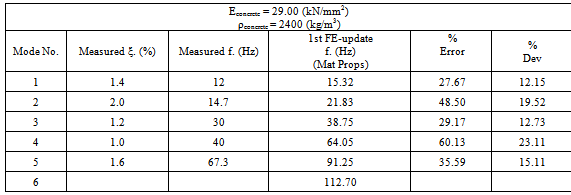
- Physical properties from the first update were kept constant while steel reinforcement was introduced in the model. There are currently confusing arguments regarding the latter[26]. The reinforcement was introduced gradually in order to observe the response of the unit. Table 3 shows the amount and type of reinforcement used. Note that distribution steel, warping control steel at corners, overlapping steel, as well as some other “features” of reinforced concrete design were not modelled. The second update was carried out and the following results were collected in Table 7 and Figure 9.
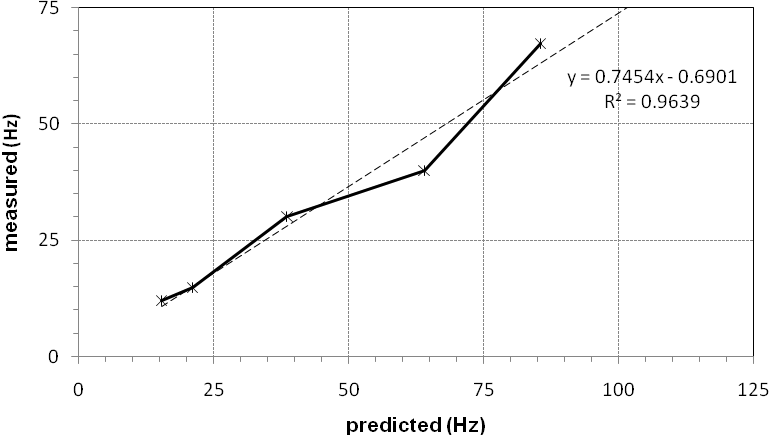 | Figure 9. Second correlation between measured and predicted natural frequencies |
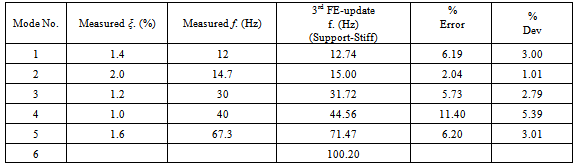
5.7. Third Update (Support Stiffness)
- The third update involved the accurate simulation of supports in the finite element model. Physical properties and steel reinforcement were kept constant this time. Support (boundary) conditions play an important role in the dynamic response of any structure. Initially, all 3 translational DOFs were restrained at one end of the terrace unit simulating a 3-dimentional pin (UX= UY= YZ= 0), using ANSYS’ built-in facility. In addition, symmetric conditions at midspan were applied with some caution. That is, a full model with a coarse mesh was used and its first six mode shapes were matched with those obtained from a symmetric model in order to make sure that any odd, non-symmetric modes would not be missed. The objective was to achieve better correlation between measured and computer predicted results. It is known that precast concrete terrace units usually rest on elastomeric bearings (bearing pads). Briefly, the pad’s multi-function is: To protect the concrete from spalling; to transfer loads smoothly and uniformly; to allow for some end rotation over the supports; to cater for differential vertical movement and levelling problems; to allow and compensate for some lateral and longitudinal ‘thermal’ movement; to act as natural vibration absorbers influencing the vibration of the units. BS2752[27] provides some information regarding specifications of chloroprene rubber compounds. ANSYS provides the user with a variety of elements with stiffness capabilities. The MATRIX27 element was chosen due to its unique aptitude to allow the analyst full control of its input parameters, and its ability to relate two nodes (one lying on the structure and the other on some fixed medium) each with 6DOF, translations along and rotations about, the nodal x, y, z axes. All matrices generated by this element are 12x12 matrices. Stiffness values were evaluated using relationships from Lindley[28] and the manufacturer’s data-sheets. Equation (12) shows the stiffness matrix developed specifically for ANSYS solver. Compr. stiffness of pad,
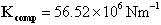 Shear stiffness of pad,
Shear stiffness of pad, 
|
|
 | Figure 10. Third correlation between measured and predicted natural frequencies |
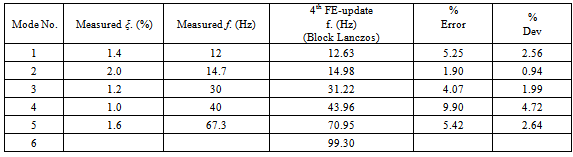
5.8. Forth Update (Block Lanczos)
- ANSYS provides the user with a variety of different solution techniques. The subspace method was initially chosen in the present study. This uses the generalised Jacobi iteration algorithm[29] which is similar to the familiar Gauss-Seidel iteration but consists in not using improved values until a step has been completed.
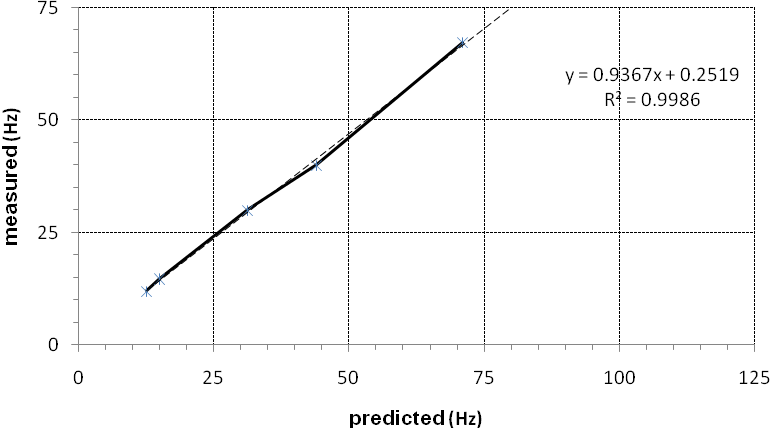 | Figure 11. Forth correlation between measured and predicted natural frequencies |
5.9. Fine Tuning
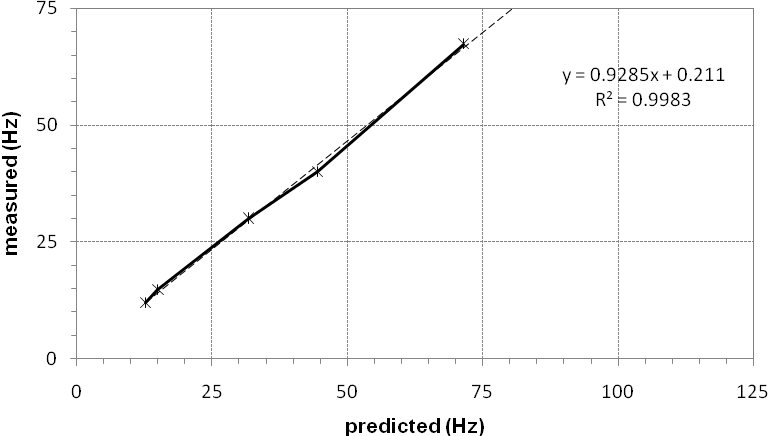
- Fine tuning was centred mainly on the material properties of concrete and was carried out in an effort to make final improvements to correlation. Hence, the modulus of elasticity of concrete was reduced slightly to 28.5 kNmm-2 and its density was increased to 2450 kgm-3. It is accepted that the former is outside the range of values given in Table 4 but within the acceptable values for C35/45 concrete. The density is still within the values given by EC2. The results from this update are presented in Table 10 and the final correlation is plotted in Figure 12. The calculated frequency values are now listed alongside, for comparison.
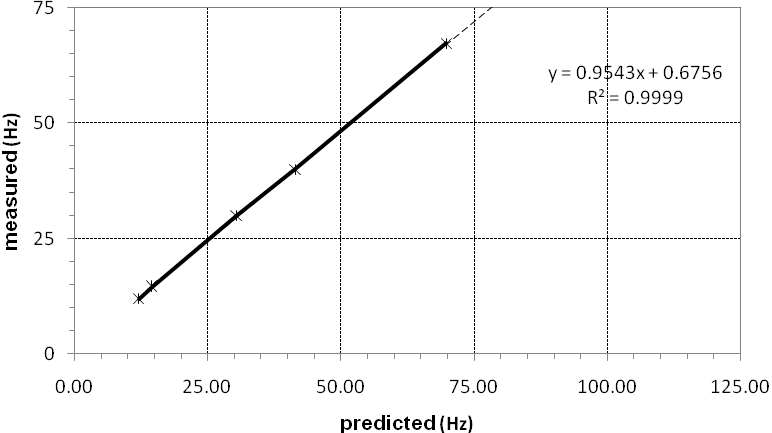 | Figure 12. ‘Fine-Tuning’ correlation between measured and predicted natural frequencies |
6. Commentary on the Results
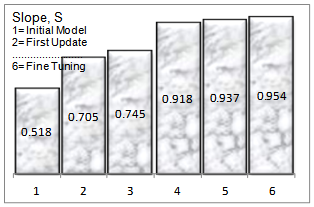
- The main debate regarding the results has taken place during the updating process in Section 5 but one or two additional comments may be of interest. The final best-fit values were out by 4.6% from the perfect correlation and although efforts were made to improve the above figure, these could not easily be justified. It is clear from the above that correlation depends on a number of variables but their degree of sensitivity is different and that obscures the process. Correlation is particularly sensitive to the physical properties of concrete and the boundary conditions of the structure considered. Figure 13 demonstrates how FE-updating improves correlation (slope). No. 1 (S= 0.518) corresponds to the initial model and No. 6 (S= 0.954) to fine tuning. The difference of 18.7% between the initial model and the first update and that of 17.3% between the third and forth updates, demonstrate the importance of the material properties and support conditions in the process.
 | Figure 13. The updating process to ‘perfect’ correlation |
|
|
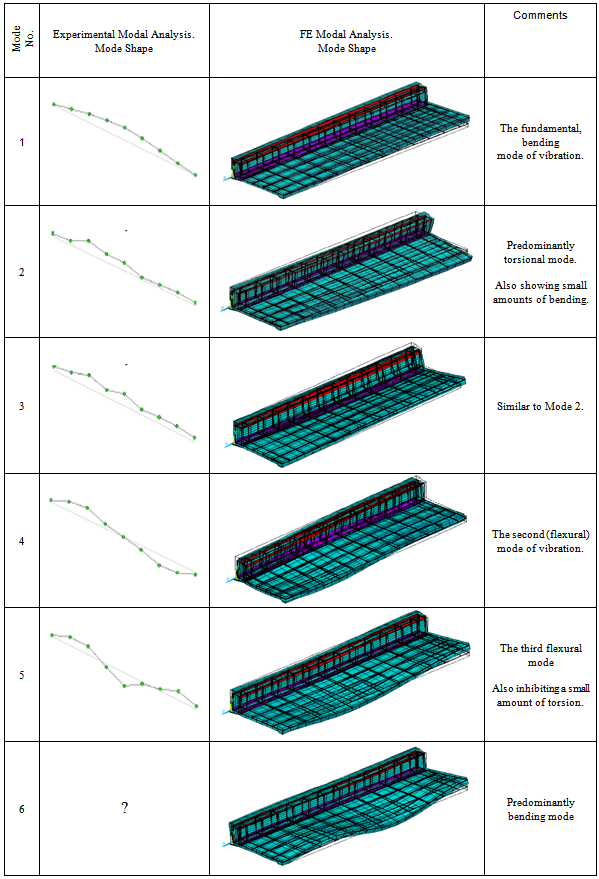
- Table 11 is dedicated to mode shapes. There is relatively good agreement between mode shapes from the experimental and the finite element modal analysis. Mode 2 is of some interest as an almost predominantly torsional mode. It would be very difficult to interpret it without the help of FEA. Note that plane symmetry has been applied to all FE-models and therefore only half the models are shown. It should be stressed again that without the help of the finite element analysis it would be difficult to interpret any complex modes based on the experimental results alone. Modes 2 and 3 represent twisting tendencies of the L-shaped terrace unit (depicted successfully in the FE analysis) whereas modes 4 and 5, may be regarded as the second and third ‘bending-like’ modes of vibration.
7. Uncertainties in Modal Analysis
- In general, the natural frequencies and mode shapes showed good correlation. As all accelerometers were positioned vertically and the structure under tests was approximated by RPs (lumped masses) in a straight line, it is reasonable to state that the experimental procedure needed assistance from the FEA in order to depict certain complex modes of vibration. The role the reinforcement plays in the dynamic behaviour of the structure can be of some interest. The basic idea is that modal parameters (notably frequencies, mode shapes, and modal damping) are functions of the physical properties of the structure (mass, damping, and stiffness). Therefore, changes in the physical properties should cause detectable changes in the modal properties.Numayar et al[27] concluded that steel reinforcement has no effect on the natural frequency of structures provided that the applied loads were kept below that causing the first crack. The same authors concluded that for applied loads greater than the cracking load, the natural frequency increases with reinforcement ratio. Feelings are mixed in this study as no clear pattern emerged. Strictly speaking, when the structure is cracked its stiffness is reduced and so should be its natural frequency. The fact that the latter is increasing means that the loss of stiffness is not significant, which is true[19].Similar studies at MSc level carried out by Pandelli and Karadelis[34] have demonstrated the change in dynamic behaviour of a simply supported, singly reinforced concrete beam of rectangular section undergoing free vibrations. It was found that increasing the amount of reinforcement is likely to increase certain modal frequencies and decrease others. Subsequently, it was noticed that reinforcing and therefore increasing the ‘specific’ stiffness of the beam may result in “forcing” the beam into a different mode of vibration and lower rather than raise its corresponding frequency. The level of sensitivity that modal parameters have to small flaws in a structure is a point of controversy among many researchers. Much of the evidence on both sides of this disagreement is anecdotal because it is only demonstrated for specific structures or systems and not proven in a fundamental sense. This issue is important for the development of health monitoring techniques because the user of such methods needs to have confidence that the damage will be recognized while the structure still has sufficient integrity to allow repair[35].It is apparent that the geometric properties of the units (asymmetric cross-section) have an effect on its flexural and torsional rigidities (EI & GJ). Clearly, the stiffness of the unit along its main span is different to that along the short span. Furthermore, as the section along the short span varies, so does its stiffness and therefore a third stiffness value may be justifiable. Some stiffness reduction related to possible cracks (shrinkage) may also be a possibility. Efforts were concentrated to assess the different stiffnesses of the unit and represent them in a smeared manner in the updating process. As a first approximation, it was decided to calculate the stiffness of the different parts of the unit such as the tread, the riser, etc and then assign modified E-values to these parts. This approach involved long computational effort and is not shown here. A purely analytical model has also been developed by the author for verification[18]. Verification does not, normally, consist part of the modal analysis procedure but may be of interest. The procedure involves the development of three partial differential equations from where the “exact” solution may be extracted. Inevitably, the equations developed depend on a series of constants such as: Econ, Gcon, Iy-y, Ix-x, Ixy, Isc, J, Iw, ex and ey, as well as their products and sums (EIsc, EIw, EIxy, GJ, Ix.Iy.Isc, (Ix + Iy), (IxIy - I2xy)) that in practice, can only be evaluated approximately. In addition, as most terms of the final frequency equation are raised to some high power, or involve products, errors can be exaggerated and accuracy compromised.
8. Concluding Notes
- A comprehensive account of experimental and numerical modal analysis for a family of reinforced concrete grandstand terraces, supported on a rectangular hollow section (RHS) frame was presented in this study. Based on the findings, the following conclusions can be drawn: • Overall, and after studying the first five modes of vibration it was found that experimentally obtained natural frequencies were in good agreement with the ones predicted by a repeatedly updated finite element model and the results obtained theoretically.• Experimental procedures may not be adequate to provide a complete account of modal analysis unless the equipment used is in abundance, of good quality, high resolution and standards and therefore extremely expensive and unsustainable for research work alone. Hence, some limitations are inevitable as certain modes that tend to be more complex than others, may not be depicted accurately by the experimental analysis. A rigorous finite element model should help to overcome this problem by capturing the resulting mode shapes with confidence and accuracy, especially at higher modes of vibration. • Initial and short term results suggest that the amount of reinforcement has little effect on the dynamic properties of the “uncracked” reinforced concrete terrace units. However, interim but carefully studied results from the finite element analysis hinted towards the possibility that an increase in the amount of reinforcement is likely to force the structure into a different mode of vibration, hence altering the previously obtained properties.• The dynamic properties of the terrace units were found to be very sensitive to two parameters, the physical properties of the main material (concrete) and the conditions of the supports of the structure. The degree of sensitivity is discussed in some detail in Sections 5 and 6. Essentially, it was found that a gradual improvement of the predicted natural frequency values was evident by progressively improving the representation of boundary conditions. Best correlation was achieved when the inserted between the units neoprene pads were modelled by simulating their stiffness characteristics with the ANSYS dedicated stiffness matrix element. • Also, it was found (section 5.1) that the subsequent adoption of Block Lanczos solution technique, over the initial choice of the subspace method, reduced the CPU-time and at the same time made a modest contribution to the accuracy of the results. It is therefore recommend for similar type of numerical analysis work. • Verification of the experimental and numerical results may not always be possible, or may sometimes be impractical due to complex mathematical calculations and a plethora of uncertainty factors arising mainly from the constants involved.
ACKNOWLEDGEMENTS
- The author would like to thank the following organisations for their help:Bison Concrete Products Ltd, The British Gaskets Group, Howgate & Lane Ltd, Al Ashwaq Rubber products Ind.
References
| [1] | Bachmann, H. “Vibrations of building structures caused by human activities, case study of a gymnasium”, Schweizer Ingenieur und Architekt, 100 (6), 104-110, 1983. |
| [2] | Allen, D.E. “Building Vibration from Human Activities”, ACI Concrete International: Design and Construction, 12 (6), 66-73, 1990. |
| [3] | Batista, R.C, Magluta, C. “Spectator induced vibration of Maracana Football Stadium”, Structural Dynamics – EURODYN 93, 985-992, 1993. |
| [4] | Interim Guidance, DTRL, DCMS. “Dynamic performance requirements for permanent grandstands subject to crowd action. Interim guidance for assessment and design”, Institution of Structural Engineers, 2001. |
| [5] | Advisory Note, DTRL, DCMS. “Dynamic Testing of Grandstands and Seating Decks” Institution of Structural Engineers, 2002. |
| [6] | Note. “Calculation of Natural Frequencies of Grandstand Seating Decks”, The Structural Engineer, IStructE, 2003. |
| [7] | Ellis B.R., Littler J.D. “Response of cantilever grandstands to crowd loads. Part 1: serviceability evaluation”. Proceedings of the Institution of Civil Engineers, Structures and Buildings 157, (SB4) Paper 12926, 235-241, 2004. |
| [8] | Ellis B.R., Littler J.D. “Response of cantilever grandstands to crowd loads. Part 2: load estimation”. Proceedings of the Institution of Civil Engineers, Structures and Buildings 157, (SB5) Paper 12927, 297-307, 2004. |
| [9] | Ellis, B.R. and Ji, T. “Dynamic testing and numerical modelling of the Cardington steel framed building from construction to completion”, The Structural Engineer, 74 (11), 186-192, 1996. |
| [10] | Reynolds, P., Pavic, A., and Ibrahim, Z. “A Remote Monitoring System for Stadia Dynamics”. Structures and Buildings, Proceedings of the Institution of Civil Engineers, 157, 385-393. ISSN 0965-0911, 2004. |
| [11] | Reynolds, P., Pavic, A., and Ibrahim, Z. “Changes of modal properties of a stadium structure occupied by a crowd”. In IMAC XXII. The 22nd International Modal Analysis Conference, Dearborn, USA, 26–29, 2004. |
| [12] | Reynolds, P., Pavic, A. and Prichard, S. “Dynamic Analysis and Testing of a High Performance Floor Structure”, International Conference on Structural Dynamics Modelling - Test, Analysis, Correlation and Validation, Madeira Island, Portugal, 339-346, 2002. |
| [13] | Swan, I.P. Reid, D.B. Fairfield, C.A. “Modelling Highway Bridge Vibrations; the effect of Support Conditions”, British Institute of Non-destructive Testing, 47 (7), 409-413, 2005. |
| [14] | Ibrahim, Z., Reynolds P. “Finite Element Modelling for Evaluating the Dynamic Characteristic of a Grandstand”. International Journal of Engineering and Technology, 4 (2), 235-244, 2007. |
| [15] | Karadelis, J.N. Experimental Modal Analysis of Grandstand Terraces, A report submitted to BISON Concrete Products Ltd, 2010, (unpublished). |
| [16] | ICATS. MODENT, MODESH, MODACQ, MESHGEN, Reference manual, Imperial College Analysis & Testing Software, London, UK, 1997. |
| [17] | Weaver, W. (Jr), Timoshenko S.P., Young D.H. Vibration Problems in Engineering, 5th ed, John Wiley & Sons, NY, 1990. |
| [18] | Karadelis, J.N. Modal Analysis of Asymmetric Terrace Units. An Analytical Approach. Proceedings of the Institution of Civil Engineers, Engineering and Computational Mechanics Journal, 2012, (submitted) |
| [19] | Karadelis, J.N. “Concrete Grandstands. Part I. Experimental Investigation”, Proceedings of the Institution of Civil Engineers, Engineering and Computational Mechanics Journal 161, Issue EM1, doi: 101680/eacm.162.1.3, 3-9, 2009. |
| [20] | Karadelis, J.N. “Concrete Grandstands. Part II. Numerical Modelling”, Proceedings of the Institution of Civil Engineers, Engineering and Computational Mechanics Journal 162, Issue EM1, doi: 101680/eacm.162.1.1, 11-21, 2009. |
| [21] | ANSYS 9.0. “Analysis User Manual”, Version 9, Tools, Chapter 15, ANSYS Inc, Houston, USA, 2005. |
| [22] | Hughes, B.P., Karadelis, J.N. “Computation of rigid pavement stiffnesses using surface deflections from the Falling Weight Deflectometer”. Proceedings, Concrete Communication Conference 98, The 8th BCA Conference on Higher Education and the Concrete Industry, Southampton University, , 87-101, ISBN: 0 7210 1540 9 (also on CD), 1998. |
| [23] | Hyo-Gyoung Kwak, Filippou, F.C. “Finite Element Analysis of Reinforced Concrete Structures under Monotonic Loads”, Structural Engineering Mechanics and Materials, PhD Thesis, Dept of Civil Engineering University of California, Berkeley, California, Report No. UCB/SEMM-90/14, 1990. |
| [24] | Ha-Wong Song, Sang-Hyo Shim, Keun-Joo Byun, and Koichi Maekawa. “Failure Analysis of Reinforced Concrete Shell Structures using Layered Shell Element with Pressure Node”, Journal of Structural Engineering, 128 (5), 655-664, 2002. |
| [25] | Sherif, A.G. & Dilger, W.H. “Analysis and deflections of reinforced concrete flat slabs”, Canadian Journal of Civil Engineering, 25 (3), 451-466, 2006. |
| [26] | Numayar, K.S., Al-Jallamdeh, S.A., Al-Akhras, N.M. “Dynamic Stiffness of Reinforced Concrete Beams”, Proceedings of the Institution of Civil Engineers, Structures and Buildings 156, , Issue: SB4, 373-379, 2003. |
| [27] | BS2752. “Chloroprene Rubber Compounds Specification”, British Standards Institution, 2003. |
| [28] | Lindley, P.B. “Engineering Design with Natural Rubber”, NR Technical Bulletin, The Natural Rubber Producers’ Research Association, Malayan Rubber Fund Board, London, 1966. |
| [29] | Mahinthakumar, G.A., Hoole, S.R.H.A. “Parallelized Element-by-Element Jacobi Conjugate Gradients Algorithm for Field Problems, and a Comparison with Other Schemes”, Applied Electromagnetics in Materials, 1, 15-28, 1990. |
| [30] | Lanczos, C. “An iterative method for the solution of the eigenvalue problem of linear differential operators”, J Res. Natural Bureau of Standards, 45, 255-282, 1950. |
| [31] | Lewis, J.G., Grimes, R.G., Simon, H.D. “A Shifted Block Lanczos Algorithm for Solving Sparse Symmetric Generalized Eigenproblems”, SIAM Journal of Matrix Analysis Applications, Society for Industrial and Applied Mathematics, 15 (1), 228-272, 1994. |
| [32] | Kim, Y.J. Block Lanczos Algorithm, PhD thesis: AD-A224, 011,Naval Postgraduate School, Monterey, California, 1989 |
| [33] | Dai, H, & Lancaster, P. Preconditioning Block Lanczos Algorithm for Solving Symmetric Eigenvalue Problems. Journal of Computational Mathematics, Vol.8, No.4, 2000, 365-374. |
| [34] | Pandelli, I. & Karadelis, J.N. “The Effect of Reinforcement on the Dynamic Properties of a Reinforced Concrete Beam”, ANSYS UK Conference, (on CD), 2003. |
| [35] | Farrar, C.R., Doebling, S.W. An Overview of Modal Based Damage Identification Methods, Los Alamos National laboratory, Los Alamos, NM |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML