Kuliyev S. A.
Azerbaijan Engineering , Architecture University, 5, Ayna Sultanova, Baku, Azerbaijan
Correspondence to: Kuliyev S. A. , Azerbaijan Engineering , Architecture University, 5, Ayna Sultanova, Baku, Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the paper, stress state of an elastic, isotropic and homogeneous weighty half-plane weakened by an elliptic hole with two rectilinear cracks is considered. The domain S occupied by a body consists of a “lower” half-plane bounded by the straightline L2 and a contour of the hole L1. The elastic medium, in addition to its specific weight at the infinity is subjected to the action of uniformly-distributed pressure of intensity q on the segment -a< t < a of a rectilinear boundary L1 of the half-plane. The hole’s contour is free from external forces. Many aspects of such problems have been considered in the papers[1; 3; 6; 7; 8; 10]. But the case that we investigate is considered for the first time (this is connected with definition of the mapping function and also complexity of acting force factors).
Keywords:
Weighty Half-Plane, Specific Weight, Elastic Medium, Compatibility Conditions, Additional Stress Uniformly Distributed Pressure, Distance Piece Coefficient
1. Introduction
The problem solution is reduced to definition of two analytic functions 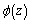 and
and 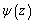 satisfying the boundary conditions. After some mathematical transformations and reasonings, we get two systems of infinite linear algebraic equations with respect to the expansion coefficients
satisfying the boundary conditions. After some mathematical transformations and reasonings, we get two systems of infinite linear algebraic equations with respect to the expansion coefficients 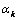 and
and 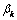 of the functions
of the functions 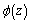 and
and 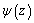 .In order to illustrate the obtained solution, numerical examples are considered. The centre of the hole coincides with the origin of coordinates
.In order to illustrate the obtained solution, numerical examples are considered. The centre of the hole coincides with the origin of coordinates 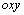 , the linear cracks are arranged symmetrically along the axis
, the linear cracks are arranged symmetrically along the axis 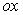 , the coordinates of the end points of the cracks are denoted by
, the coordinates of the end points of the cracks are denoted by 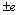 (fig.1). The domain
(fig.1). The domain 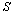 occupied by a body consists of a “lower” half-plane bounded by a straight line
occupied by a body consists of a “lower” half-plane bounded by a straight line 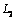 and contour of the hole
and contour of the hole 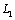 (an ellipse with two linear cracks). The problem on definition of stresses in domain
(an ellipse with two linear cracks). The problem on definition of stresses in domain  occupied by an elastic medium has a great value in such a statement in the practice of mining, tunnel building (metrobuilding) and also in many problems of hydro engineering.
occupied by an elastic medium has a great value in such a statement in the practice of mining, tunnel building (metrobuilding) and also in many problems of hydro engineering.
2. The Problem for a Weighty Half-plane
On the base of the known principle of mechanics – independence of actions of applied forces, the problem may be divided into two separate cases, the problem for a weightyhalf-plane, and a problem for a weightless half-plane under the action of uniformly distributed pressure  .
.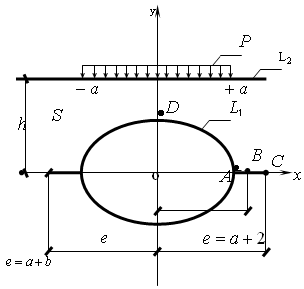 | Figure 1. Cross-section of a half-plane with the elliptic holes and two cracks. |
In the domain  of a half plane bounded by the straight line
of a half plane bounded by the straight line 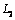 and contour of holes
and contour of holes 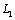 (ellipse with two linear cracks) the stress components
(ellipse with two linear cracks) the stress components 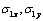 and
and 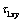 satisfy the differential equilibrium equations and compatibility conditions (for the first case of the weighty half-plane).
satisfy the differential equilibrium equations and compatibility conditions (for the first case of the weighty half-plane).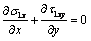 ;
; 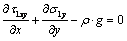 ;
; 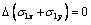 | (2.1) |
where 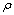 is density of elastic medium, g is free fall acceleration.The boundary conditions:
is density of elastic medium, g is free fall acceleration.The boundary conditions: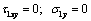 on the linear boundary L2 (2.2)
on the linear boundary L2 (2.2) on the contour of the hole
on the contour of the hole 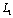 , (2.3)where
, (2.3)where  is normal to
is normal to  and
and 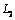 directed from the interior of the domain
directed from the interior of the domain 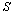 to the outside.Each of the stresses
to the outside.Each of the stresses 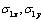 and
and 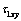 may be represented in the form of the sum [3:9]:
may be represented in the form of the sum [3:9]: ;
;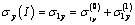 ;
;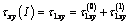 | (2.4) |
where: 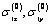 and
and 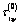 are stresses in solid (without holes) weighty half-plane with the indicated above acting forces (uniformly distributed pressure on the segment
are stresses in solid (without holes) weighty half-plane with the indicated above acting forces (uniformly distributed pressure on the segment 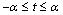 of the linear boundary
of the linear boundary 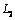 ) and are some special solutions of differential equations (2.1).The constituents
) and are some special solutions of differential equations (2.1).The constituents 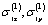 and
and 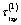 are additional stresses stipulated by the availability of the hole
are additional stresses stipulated by the availability of the hole 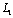 in medium that weakens it.Since the components
in medium that weakens it.Since the components 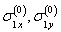 and
and 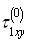 satisfy equations (2.1), (as special solution of these systems of equations), we can take them in the form[3;9]:
satisfy equations (2.1), (as special solution of these systems of equations), we can take them in the form[3;9]: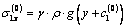 ;
;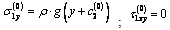 | (2.5) |
Here, 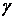 is a constant dependent on medium’s property, so called a distance piece factor; for a considerable depth,
is a constant dependent on medium’s property, so called a distance piece factor; for a considerable depth, 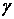 is very close to a unit. The integration constants
is very close to a unit. The integration constants 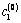 and
and 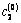 should be defined from the condition of inversion of the components
should be defined from the condition of inversion of the components 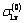 and
and 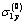 in
in 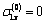 and
and 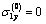 , respectively on the linear boundary L2. In (2.5), by accepting
, respectively on the linear boundary L2. In (2.5), by accepting 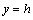 , we get
, we get 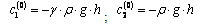 | (2.6) |
Thus, the components 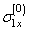 and
and 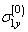 will take the form:
will take the form: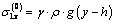 ;
;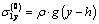 | (2.7) |
The stress components 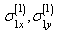 and
and 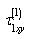 satisfy the homogeneous system of equilibrium equations and compatibility equations (2.1) assuming that they vanish at infinity and on the linear boundary
satisfy the homogeneous system of equilibrium equations and compatibility equations (2.1) assuming that they vanish at infinity and on the linear boundary 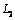 .So, we have:
.So, we have: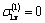 ;
; 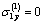 on
on 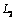 (2.8)
(2.8)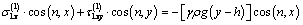
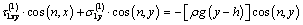 on
on 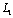 . (2.9)Since the contour
. (2.9)Since the contour 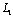 is free from external forces, then for releasing the stresses
is free from external forces, then for releasing the stresses 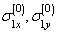 and
and 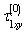 from this contour we should apply the forces with opposite sign
from this contour we should apply the forces with opposite sign 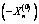 and
and 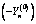 . In the present case, we are interested mainly in the stress state in the vicinity of the contour
. In the present case, we are interested mainly in the stress state in the vicinity of the contour 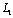 (ellipse with two linear cracks) including at the end points of the cracks
(ellipse with two linear cracks) including at the end points of the cracks 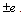 Therewith, taking into account the conditions
Therewith, taking into account the conditions 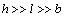 (for considerable depth of medium), not making any series error, we can reject exact satisfaction of boundary condition (2.8) and in expression (2.9) neglect the quantity
(for considerable depth of medium), not making any series error, we can reject exact satisfaction of boundary condition (2.8) and in expression (2.9) neglect the quantity 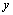 contained in parenthesis of the right hand side. Thus, condition (2.9) is reduced to the form:
contained in parenthesis of the right hand side. Thus, condition (2.9) is reduced to the form: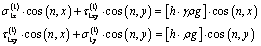 | (2.10) |
We can introduce the functions 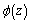 and
and 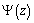 of the complex variable
of the complex variable 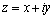 that are regular in domain
that are regular in domain 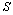 and connected with stress components
and connected with stress components 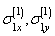 and
and 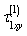 by Kolosov – Muskheleshvili – Sherman formulae:
by Kolosov – Muskheleshvili – Sherman formulae: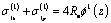 ;
;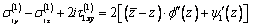 | (2.11) |
Taking into account these expressions, boundary conditions (2.10) are transformed to the following form: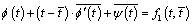 on
on  (2.12)
(2.12)
3. Problem for a Weightless Half-Plane under the Action of Uniformly Distributed Pressure P
In the second case, when a uniformly – distributed load of intensity 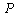 acts on the linear boundary
acts on the linear boundary 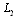 on the segment
on the segment 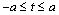 , the stresses
, the stresses 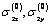 and
and 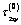 for an entire weightless half-plane are determined by the expressions [1;6]:
for an entire weightless half-plane are determined by the expressions [1;6]: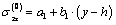 ;
;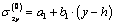 ;
;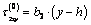 | (3.1) |
where 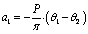 ;
;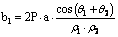 ;
; 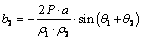 ;
;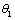 and
and 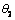 are the angles under which the loaded segment
are the angles under which the loaded segment 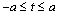 from the point
from the point 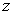 of a half-plane is seen,
of a half-plane is seen, 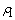 and
and 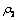 are the distances from the point
are the distances from the point 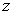 to the end of the segment
to the end of the segment 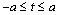 (i.e. to the point
(i.e. to the point 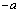 and
and 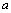 on the linear boundary
on the linear boundary 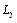 ).In the present case, the additional stresses
).In the present case, the additional stresses 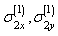 and
and 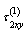 , stipulated by availability of a hole satisfy the following boundary conditions (similar to the first case, i.e. formulae 2.4). Each of the stresses
, stipulated by availability of a hole satisfy the following boundary conditions (similar to the first case, i.e. formulae 2.4). Each of the stresses 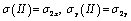 and
and 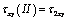 are represented in the form of the sum
are represented in the form of the sum | (3.2) |
Similar to the first problem, the stress components 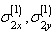 and
and 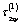 are defined by analytic functions by the known formulae (see. 2.11). Then, boundary conditions (3.2) are transformed also to the following form
are defined by analytic functions by the known formulae (see. 2.11). Then, boundary conditions (3.2) are transformed also to the following form 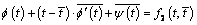 | (3.3) |
In equations (2.12) and (3.3), the variable 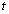 is an affix of the points of the contour
is an affix of the points of the contour 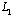 as for a weighty half-plane (the first problem):
as for a weighty half-plane (the first problem):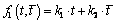 ;
;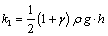 ;
;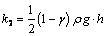 | (3.4) |
At a considerable depth 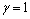 , then we get
, then we get 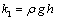 ;
; 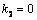 For a weightless half-plane, under the action the uniformly-distributed load of intensity P, on the segment
For a weightless half-plane, under the action the uniformly-distributed load of intensity P, on the segment 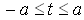 , of the boundary L2 , the right side of equation (3.3) has the form [1;6;7]:
, of the boundary L2 , the right side of equation (3.3) has the form [1;6;7]: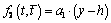 ;
;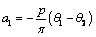 | (3.5) |
It is seen that boundary conditions for determining additional stresses at both variants of active external forces are reduced to determining two analytic functions 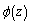 and
and 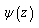 (by comparing 2.12 and 3.3 it is seen that the left side are same in both cases, the right side has the form of 3.4 and 3.5, respectively).For both variants, the desired functions
(by comparing 2.12 and 3.3 it is seen that the left side are same in both cases, the right side has the form of 3.4 and 3.5, respectively).For both variants, the desired functions 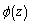 and
and 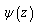 are representable in the form [3-10].
are representable in the form [3-10].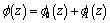 ;
;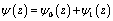 | (3.6) |
Here, 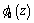 and
and 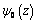 are analytic functions regular everywhere in the lower half-plane, with a rectilinear boundary
are analytic functions regular everywhere in the lower half-plane, with a rectilinear boundary 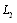 ,
, 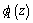 and
and 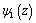 are holomorphic functions in domain outside of the hole
are holomorphic functions in domain outside of the hole 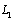 (ellipse with two rectilinear cracks).The functions
(ellipse with two rectilinear cracks).The functions 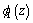 and
and 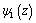 regular outside of the contour L1 (outside of the hole) are representable in the form [1;6;9;10]
regular outside of the contour L1 (outside of the hole) are representable in the form [1;6;9;10]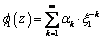 ;
;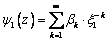 | (3.7) |
Assuming that the coefficients 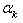 and
and 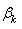 in expansions (3.7) are known, by the Muskheleshvili method (the method based on the use of a Cauchy type integral) on the linear boundary
in expansions (3.7) are known, by the Muskheleshvili method (the method based on the use of a Cauchy type integral) on the linear boundary 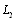 from the boundary condition 2.12 or from 3.3 for
from the boundary condition 2.12 or from 3.3 for 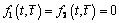 we find the functions
we find the functions 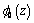 and
and 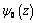
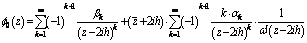
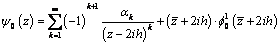 | (3.8) |
We should recall that the following expressions hold on the linear boundary 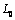 :
: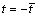 ;
; 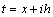 ;
; 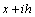 ;
; 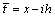 ;
; 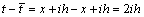 ;
; 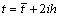 ;
; 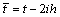 .Now, pass to boundary conditions on the contour of the hole
.Now, pass to boundary conditions on the contour of the hole 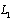 .The exterior of the contour
.The exterior of the contour 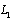 (ellipse with two rectilinear cracks) is mapped onto the exterior of a unit circle by means of the function [4;5].
(ellipse with two rectilinear cracks) is mapped onto the exterior of a unit circle by means of the function [4;5].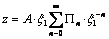 ;
; 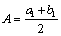 ;
;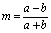 | (3.9) |
where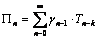 ;
; 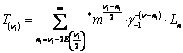 .The quantities
.The quantities 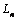 are determined according to[4;5] from the following condition
are determined according to[4;5] from the following condition 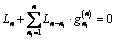 | (3.10) |
where 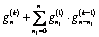 ;
; 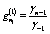 The function
The function 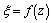 inverse to the mapping function (3.9) is found in the form [4;5]:
inverse to the mapping function (3.9) is found in the form [4;5]: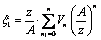 | (3.11) |
Where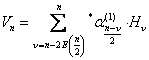 ;
; 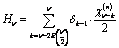 ;The quantities
;The quantities 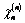 are determined similar to the quantities
are determined similar to the quantities 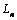 replacing in (3.10)
replacing in (3.10) 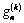 by
by 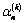 , moreover
, moreover 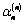 will be defined from the recurrent formula (3.11) having taken
will be defined from the recurrent formula (3.11) having taken 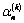 instead of
instead of 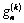 .For an ellipse, the first six quantities
.For an ellipse, the first six quantities 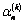 ,
,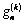 are found and arranged in the table (see. [4;5]).Allowing for expansions (3.6), (3.7), (3.8) and (3.9), boundary condition (2.12) or (3.3) on the contour of the hole
are found and arranged in the table (see. [4;5]).Allowing for expansions (3.6), (3.7), (3.8) and (3.9), boundary condition (2.12) or (3.3) on the contour of the hole 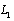 is reduced to the form (after some mathematical transformations and reasonings, passing to a new variable
is reduced to the form (after some mathematical transformations and reasonings, passing to a new variable 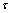 , and taking into account that
, and taking into account that 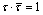 holds on a unit circle):
holds on a unit circle): | (3.12) |
where 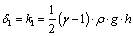 ;
; 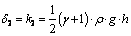 for a weighty half-plane.
for a weighty half-plane.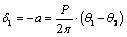 ,
,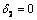 for a weightless half-plane under the action of a uniformly distributed load of intensity
for a weightless half-plane under the action of a uniformly distributed load of intensity 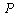 on the segment
on the segment 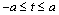 of the rectilinear boundary L0.In equation (3.12) having equated the coefficients under the same degrees of
of the rectilinear boundary L0.In equation (3.12) having equated the coefficients under the same degrees of 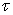 , we get the following two systems of infinite algebraic equations for determining the coefficients
, we get the following two systems of infinite algebraic equations for determining the coefficients 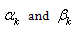 :
: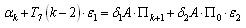 | (3.13) |
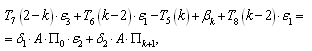 | (3.14) |
where: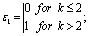
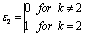 ;
;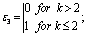 The values of the quantities
The values of the quantities  are not cited here because of their bulky form.Solving jointly systems of equations (3.13) and (3.14) (having taken some first terms from each system), the coefficients
are not cited here because of their bulky form.Solving jointly systems of equations (3.13) and (3.14) (having taken some first terms from each system), the coefficients 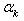 and
and 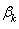 are determined. Analytic functions
are determined. Analytic functions 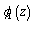 and
and 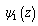 are determined for each of indicated problems respectively, from formula (3.7). Having known the values of the functions
are determined for each of indicated problems respectively, from formula (3.7). Having known the values of the functions 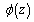 and
and 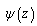 , the additional stresses
, the additional stresses 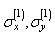 and
and 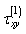 are determined by formula (2.11). The found stress components
are determined by formula (2.11). The found stress components 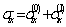 ,
, 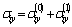 and
and 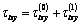 ;
; 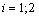 for each of the mentioned variants of active loads are given below (calculated at typical points of the holes
for each of the mentioned variants of active loads are given below (calculated at typical points of the holes 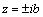 ;
; 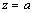 for
for 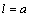 , where
, where 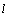 is the length of the aperture and also at the points
is the length of the aperture and also at the points 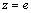 , for
, for 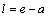 ).On the base of force action independence principle, by the superposition method we can determine stress state under simultaneous action of loads indicated in both cases:
).On the base of force action independence principle, by the superposition method we can determine stress state under simultaneous action of loads indicated in both cases: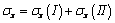 ;
;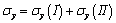 ;
;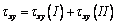 | (3.15) |
where 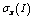 ,
, 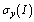 and
and 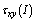 belong to the first,
belong to the first, 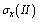 ,
, 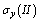 and
and 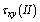 to the second problem.
to the second problem.
4. Numerical Results
4.1. Uniformly Distributed Pressure of Intensity 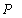 Acts on a Rectilinear Boundary
Acts on a Rectilinear Boundary 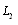 of a Weightless Half-Plane on the Segment
of a Weightless Half-Plane on the Segment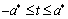
For an entire (without hole) half-plane, this problem has been solved in [1;6;7;8]. Using the obtained results for an entire half-plane by the method indicated above, i.e. solving the system of equations (3.13 and 3.14) for the right side in the form (3.12), by the known formulae (2.11) we find additional stresses stipulated by the availability of a hole. The value of complete – total stresses for different variants for dimensions of a hole and depth 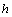 are the followings: (for typical points of the hole)Variant I:
are the followings: (for typical points of the hole)Variant I: 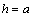 ;
; 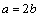 ;
;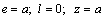 ; the point «
; the point « » in the draft
» in the draft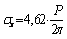 ;
; 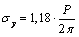
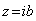 at the point «
at the point «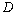 ».
».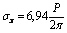 ;
; 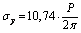 for
for 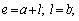 at the point
at the point 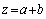 ;
;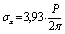 ;
; 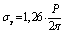 for
for 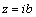 ;
;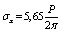 ;
; 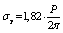 .for
.for 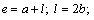 at the point
at the point 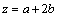 ;
;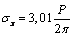 ;
;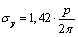 .Variant II:
.Variant II: 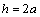 ;
; 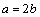 ;
; 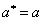 ;
;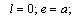 at the point
at the point 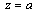 ;
; 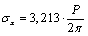 ;
; 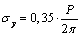 ; For
; For 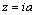 ;
; 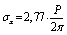 ;
; 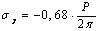 ;
; 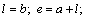 at the point
at the point 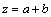 ;
; 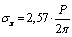 ;
; 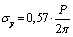 ;Variant III:
;Variant III: 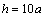 ;
; 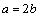 ;
; 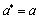
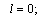 at the points
at the points 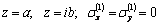 i.e. at considerable depths the additional stresses equal to zero (influence of a hole and load on a rectilinear boundary
i.e. at considerable depths the additional stresses equal to zero (influence of a hole and load on a rectilinear boundary 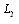 almost doesn’t influence the stress distribution).
almost doesn’t influence the stress distribution).
4.2. A weighty Half-Plane Weakened by a Hole 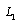 (Ellipse with Two Rectilinear Cracks) is Subjected Only to the Action of Gravity
(Ellipse with Two Rectilinear Cracks) is Subjected Only to the Action of Gravity
The contours 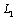 and
and 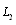 are free from external forces. Solving the system of equations for the right side in the form (3.12), we define the desired coefficients
are free from external forces. Solving the system of equations for the right side in the form (3.12), we define the desired coefficients 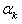 and
and 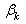 for different relative dimensions. Then, by formula (2.11) we find additional (as the result, total stresses) stresses:
for different relative dimensions. Then, by formula (2.11) we find additional (as the result, total stresses) stresses: 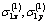 and
and 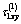 at the typical points of the hole
at the typical points of the hole 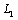 (since we are interested only in stress concentration at the points of hole’s contour). Below we give the found values of these stresses for different variants:Variant I:
(since we are interested only in stress concentration at the points of hole’s contour). Below we give the found values of these stresses for different variants:Variant I: 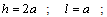
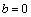 for
for 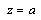 ;
; 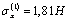 ;
;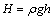 ;
; 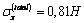 ;for
;for 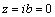 ;
; ;
;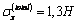 .Variant II:
.Variant II: 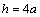 ;
;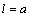 ;
;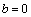 for
for 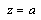 ;
; 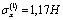 ;
; 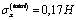 при
при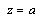 ;
; 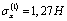 ;
; 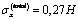 .Variant III:
.Variant III: 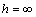 ;
; 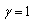 (distance piece factor equals to one), then at all the points of the contour
(distance piece factor equals to one), then at all the points of the contour 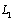 we have
we have 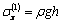 ;
;  .
.
5. Conclusions
The quantities of additional 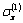 and total stresses on the
and total stresses on the 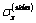 of a rectilinear aperture (i.e. at the end points of the crack and in the middle of this crack when
of a rectilinear aperture (i.e. at the end points of the crack and in the middle of this crack when 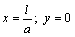 ) considerably increase when the crack of
) considerably increase when the crack of 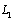 approaches to the linear contour
approaches to the linear contour 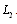 As calculations show, such type stresses have a particular local character and as a rule, they rapidly drop (weaken) when they are removed from the vertex of the crack, where they have maximal value. When
As calculations show, such type stresses have a particular local character and as a rule, they rapidly drop (weaken) when they are removed from the vertex of the crack, where they have maximal value. When 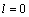 ,
, 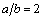 ;
; 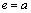 the internal contour
the internal contour  will become an ellipse, and the problem on definition of additional stresses will be similar to that in the paper[9]. Therefore, here we don’t cite the results.
will become an ellipse, and the problem on definition of additional stresses will be similar to that in the paper[9]. Therefore, here we don’t cite the results.Notes
1The method elaborated by N. I. Muskheleshvili [6] is based on the use of a Cauchy type integral. For example: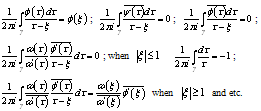
References
| [1] | Amanzadeh Yu. A. Theory of elasticity. М. Vysshaya shkola 1976. 272 p. (Russian) |
| [2] | Berezhnitskiy L. T., Delyavskiy M. V., Panasyuk V. V. Bending of elastic plates with crack type defects. Kiev, Naukova Dumka, 1979. 400 p. (Russian) |
| [3] | Kosmodomianskiy A. S. Plane problem of theory of elasticity for plates with holes, cuts and bulgs. Kiev. Vysshaya Shkola. 1975. 227 p. (Russian) |
| [4] | Kuliyev S. A. Two-dimensional problems of theory of elasticity. M. Stroyizdat 1991, 351 p. (Russian) |
| [5] | Kuliyev S. A. Conformally-mapping functions of complex domains. Baku, Azerneshr. 2004, 372 p. (Russian) |
| [6] | Muskheleshvili N. I. Some basic problems of mathematical theory of elasticity. M. Nauka, 1966, 707 p. (Russian) |
| [7] | Savin T. N. Stress distribution near holes. Kiev, Naukova dumka, 1968, 887 p. (Russian) |
| [8] | Timoshenko S. R., Goodyear Dt. Theory of elasticity M. Nauka, 1975, 575 p. (Russian) |
| [9] | Sherman D. I. Elastic weighty half-plane weakened by an elliptic from hole arranged close to its boundary. Collection: Problemy mechaniki sploshnoy sredy: M. Izd-vo ANSSSR, 1961. pp. 527-563. (Russian) |
| [10] | Sherman D. I. On stresses of weighty half-plane weakened by two annular holes. PMM, 1952, vol. ХV, issue 3. pp. 297-316. (Russian) |
| [11] | Sie s., Paris P., Erdogan F. Coefficients of stress concentration at the vertex of the crack under plane tension and bending of plates. // Tr. Amer. Obsh. inzh. mech. Ser. E. Prikl. Mekh. 1962. №2, pp.102-108. |

 and
and 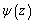 satisfying the boundary conditions. After some mathematical transformations and reasonings, we get two systems of infinite linear algebraic equations with respect to the expansion coefficients
satisfying the boundary conditions. After some mathematical transformations and reasonings, we get two systems of infinite linear algebraic equations with respect to the expansion coefficients 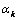 and
and 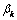 of the functions
of the functions 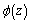 and
and 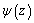 .In order to illustrate the obtained solution, numerical examples are considered. The centre of the hole coincides with the origin of coordinates
.In order to illustrate the obtained solution, numerical examples are considered. The centre of the hole coincides with the origin of coordinates 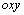 , the linear cracks are arranged symmetrically along the axis
, the linear cracks are arranged symmetrically along the axis 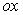 , the coordinates of the end points of the cracks are denoted by
, the coordinates of the end points of the cracks are denoted by 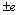 (fig.1). The domain
(fig.1). The domain 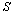 occupied by a body consists of a “lower” half-plane bounded by a straight line
occupied by a body consists of a “lower” half-plane bounded by a straight line 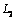 and contour of the hole
and contour of the hole 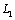 (an ellipse with two linear cracks). The problem on definition of stresses in domain
(an ellipse with two linear cracks). The problem on definition of stresses in domain 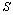 occupied by an elastic medium has a great value in such a statement in the practice of mining, tunnel building (metrobuilding) and also in many problems of hydro engineering.
occupied by an elastic medium has a great value in such a statement in the practice of mining, tunnel building (metrobuilding) and also in many problems of hydro engineering.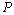 .
.
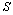 of a half plane bounded by the straight line
of a half plane bounded by the straight line 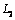 and contour of holes
and contour of holes 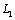 (ellipse with two linear cracks) the stress components
(ellipse with two linear cracks) the stress components 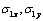 and
and 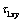 satisfy the differential equilibrium equations and compatibility conditions (for the first case of the weighty half-plane).
satisfy the differential equilibrium equations and compatibility conditions (for the first case of the weighty half-plane).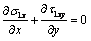 ;
; 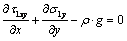 ;
; 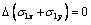
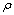 is density of elastic medium, g is free fall acceleration.The boundary conditions:
is density of elastic medium, g is free fall acceleration.The boundary conditions: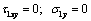 on the linear boundary L2 (2.2)
on the linear boundary L2 (2.2) on the contour of the hole
on the contour of the hole 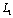 , (2.3)where
, (2.3)where 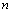 is normal to
is normal to 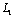 and
and 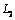 directed from the interior of the domain
directed from the interior of the domain 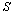 to the outside.Each of the stresses
to the outside.Each of the stresses 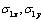 and
and 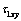 may be represented in the form of the sum [3:9]:
may be represented in the form of the sum [3:9]: ;
;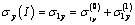 ;
;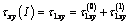
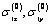 and
and 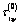 are stresses in solid (without holes) weighty half-plane with the indicated above acting forces (uniformly distributed pressure on the segment
are stresses in solid (without holes) weighty half-plane with the indicated above acting forces (uniformly distributed pressure on the segment 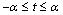 of the linear boundary
of the linear boundary  ) and are some special solutions of differential equations (2.1).The constituents
) and are some special solutions of differential equations (2.1).The constituents 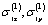 and
and 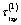 are additional stresses stipulated by the availability of the hole
are additional stresses stipulated by the availability of the hole 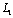 in medium that weakens it.Since the components
in medium that weakens it.Since the components 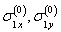 and
and 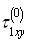 satisfy equations (2.1), (as special solution of these systems of equations), we can take them in the form[3;9]:
satisfy equations (2.1), (as special solution of these systems of equations), we can take them in the form[3;9]: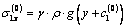 ;
;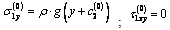
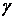 is a constant dependent on medium’s property, so called a distance piece factor; for a considerable depth,
is a constant dependent on medium’s property, so called a distance piece factor; for a considerable depth, 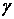 is very close to a unit. The integration constants
is very close to a unit. The integration constants 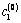 and
and 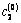 should be defined from the condition of inversion of the components
should be defined from the condition of inversion of the components 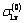 and
and 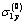 in
in 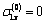 and
and 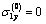 , respectively on the linear boundary L2. In (2.5), by accepting
, respectively on the linear boundary L2. In (2.5), by accepting 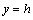 , we get
, we get 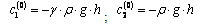
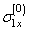 and
and 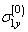 will take the form:
will take the form: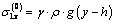 ;
;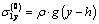
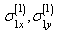 and
and 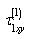 satisfy the homogeneous system of equilibrium equations and compatibility equations (2.1) assuming that they vanish at infinity and on the linear boundary
satisfy the homogeneous system of equilibrium equations and compatibility equations (2.1) assuming that they vanish at infinity and on the linear boundary 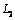 .So, we have:
.So, we have: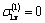 ;
; 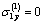 on
on  (2.8)
(2.8)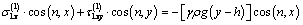
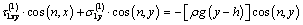 on
on 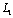 . (2.9)Since the contour
. (2.9)Since the contour 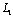 is free from external forces, then for releasing the stresses
is free from external forces, then for releasing the stresses 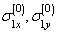 and
and 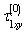 from this contour we should apply the forces with opposite sign
from this contour we should apply the forces with opposite sign 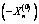 and
and 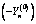 . In the present case, we are interested mainly in the stress state in the vicinity of the contour
. In the present case, we are interested mainly in the stress state in the vicinity of the contour 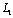 (ellipse with two linear cracks) including at the end points of the cracks
(ellipse with two linear cracks) including at the end points of the cracks 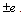 Therewith, taking into account the conditions
Therewith, taking into account the conditions 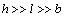 (for considerable depth of medium), not making any series error, we can reject exact satisfaction of boundary condition (2.8) and in expression (2.9) neglect the quantity
(for considerable depth of medium), not making any series error, we can reject exact satisfaction of boundary condition (2.8) and in expression (2.9) neglect the quantity 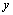 contained in parenthesis of the right hand side. Thus, condition (2.9) is reduced to the form:
contained in parenthesis of the right hand side. Thus, condition (2.9) is reduced to the form: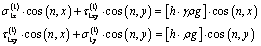
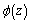 and
and 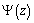 of the complex variable
of the complex variable 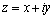 that are regular in domain
that are regular in domain 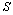 and connected with stress components
and connected with stress components 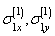 and
and 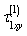 by Kolosov – Muskheleshvili – Sherman formulae:
by Kolosov – Muskheleshvili – Sherman formulae: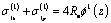 ;
;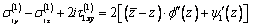
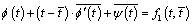 on
on 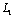 (2.12)
(2.12)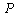 acts on the linear boundary
acts on the linear boundary 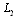 on the segment
on the segment 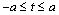 , the stresses
, the stresses 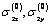 and
and 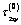 for an entire weightless half-plane are determined by the expressions [1;6]:
for an entire weightless half-plane are determined by the expressions [1;6]: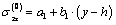 ;
;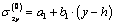 ;
;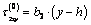
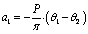 ;
;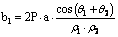 ;
; 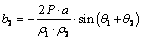 ;
;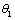 and
and 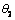 are the angles under which the loaded segment
are the angles under which the loaded segment 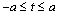 from the point
from the point 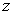 of a half-plane is seen,
of a half-plane is seen, 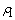 and
and 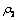 are the distances from the point
are the distances from the point 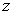 to the end of the segment
to the end of the segment 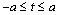 (i.e. to the point
(i.e. to the point 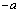 and
and 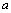 on the linear boundary
on the linear boundary 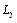 ).In the present case, the additional stresses
).In the present case, the additional stresses 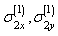 and
and 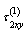 , stipulated by availability of a hole satisfy the following boundary conditions (similar to the first case, i.e. formulae 2.4). Each of the stresses
, stipulated by availability of a hole satisfy the following boundary conditions (similar to the first case, i.e. formulae 2.4). Each of the stresses 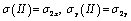 and
and 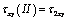 are represented in the form of the sum
are represented in the form of the sum
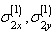 and
and 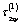 are defined by analytic functions by the known formulae (see. 2.11). Then, boundary conditions (3.2) are transformed also to the following form
are defined by analytic functions by the known formulae (see. 2.11). Then, boundary conditions (3.2) are transformed also to the following form 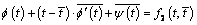
 is an affix of the points of the contour
is an affix of the points of the contour 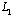 as for a weighty half-plane (the first problem):
as for a weighty half-plane (the first problem):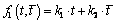 ;
;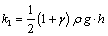 ;
;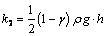
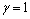 , then we get
, then we get 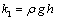 ;
; 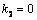 For a weightless half-plane, under the action the uniformly-distributed load of intensity P, on the segment
For a weightless half-plane, under the action the uniformly-distributed load of intensity P, on the segment 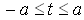 , of the boundary L2 , the right side of equation (3.3) has the form [1;6;7]:
, of the boundary L2 , the right side of equation (3.3) has the form [1;6;7]: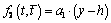 ;
;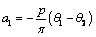
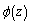 and
and 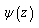 (by comparing 2.12 and 3.3 it is seen that the left side are same in both cases, the right side has the form of 3.4 and 3.5, respectively).For both variants, the desired functions
(by comparing 2.12 and 3.3 it is seen that the left side are same in both cases, the right side has the form of 3.4 and 3.5, respectively).For both variants, the desired functions 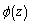 and
and 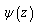 are representable in the form [3-10].
are representable in the form [3-10].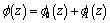 ;
;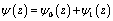
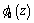 and
and 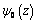 are analytic functions regular everywhere in the lower half-plane, with a rectilinear boundary
are analytic functions regular everywhere in the lower half-plane, with a rectilinear boundary 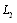 ,
, 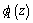 and
and 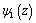 are holomorphic functions in domain outside of the hole
are holomorphic functions in domain outside of the hole 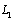 (ellipse with two rectilinear cracks).The functions
(ellipse with two rectilinear cracks).The functions 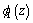 and
and 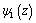 regular outside of the contour L1 (outside of the hole) are representable in the form [1;6;9;10]
regular outside of the contour L1 (outside of the hole) are representable in the form [1;6;9;10]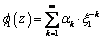 ;
;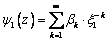
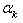 and
and 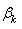 in expansions (3.7) are known, by the Muskheleshvili method (the method based on the use of a Cauchy type integral) on the linear boundary
in expansions (3.7) are known, by the Muskheleshvili method (the method based on the use of a Cauchy type integral) on the linear boundary 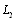 from the boundary condition 2.12 or from 3.3 for
from the boundary condition 2.12 or from 3.3 for 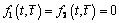 we find the functions
we find the functions 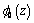 and
and 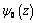
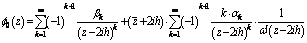
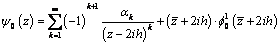
 :
: ;
; 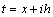 ;
; 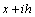 ;
; 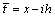 ;
; 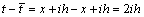 ;
; 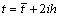 ;
; 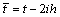 .Now, pass to boundary conditions on the contour of the hole
.Now, pass to boundary conditions on the contour of the hole 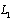 .The exterior of the contour
.The exterior of the contour 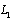 (ellipse with two rectilinear cracks) is mapped onto the exterior of a unit circle by means of the function [4;5].
(ellipse with two rectilinear cracks) is mapped onto the exterior of a unit circle by means of the function [4;5].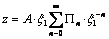 ;
; 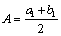 ;
;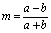
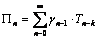 ;
; 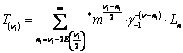 .The quantities
.The quantities 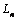 are determined according to[4;5] from the following condition
are determined according to[4;5] from the following condition 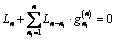
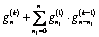 ;
; 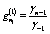 The function
The function 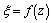 inverse to the mapping function (3.9) is found in the form [4;5]:
inverse to the mapping function (3.9) is found in the form [4;5]: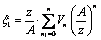
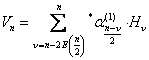 ;
; 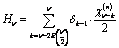 ;The quantities
;The quantities 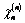 are determined similar to the quantities
are determined similar to the quantities 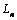 replacing in (3.10)
replacing in (3.10) 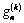 by
by 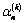 , moreover
, moreover 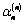 will be defined from the recurrent formula (3.11) having taken
will be defined from the recurrent formula (3.11) having taken 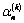 instead of
instead of 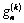 .For an ellipse, the first six quantities
.For an ellipse, the first six quantities 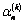 ,
,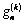 are found and arranged in the table (see. [4;5]).Allowing for expansions (3.6), (3.7), (3.8) and (3.9), boundary condition (2.12) or (3.3) on the contour of the hole
are found and arranged in the table (see. [4;5]).Allowing for expansions (3.6), (3.7), (3.8) and (3.9), boundary condition (2.12) or (3.3) on the contour of the hole 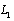 is reduced to the form (after some mathematical transformations and reasonings, passing to a new variable
is reduced to the form (after some mathematical transformations and reasonings, passing to a new variable 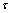 , and taking into account that
, and taking into account that 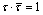 holds on a unit circle):
holds on a unit circle):
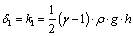 ;
; 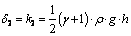 for a weighty half-plane.
for a weighty half-plane.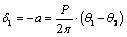 ,
,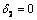 for a weightless half-plane under the action of a uniformly distributed load of intensity
for a weightless half-plane under the action of a uniformly distributed load of intensity 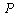 on the segment
on the segment 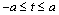 of the rectilinear boundary L0.In equation (3.12) having equated the coefficients under the same degrees of
of the rectilinear boundary L0.In equation (3.12) having equated the coefficients under the same degrees of 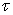 , we get the following two systems of infinite algebraic equations for determining the coefficients
, we get the following two systems of infinite algebraic equations for determining the coefficients 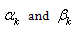 :
: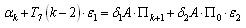
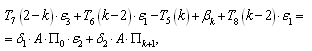
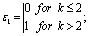
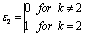 ;
;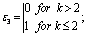 The values of the quantities
The values of the quantities  are not cited here because of their bulky form.Solving jointly systems of equations (3.13) and (3.14) (having taken some first terms from each system), the coefficients
are not cited here because of their bulky form.Solving jointly systems of equations (3.13) and (3.14) (having taken some first terms from each system), the coefficients 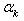 and
and 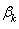 are determined. Analytic functions
are determined. Analytic functions 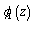 and
and 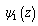 are determined for each of indicated problems respectively, from formula (3.7). Having known the values of the functions
are determined for each of indicated problems respectively, from formula (3.7). Having known the values of the functions 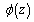 and
and 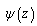 , the additional stresses
, the additional stresses 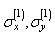 and
and 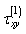 are determined by formula (2.11). The found stress components
are determined by formula (2.11). The found stress components 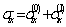 ,
, 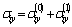 and
and 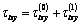 ;
; 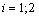 for each of the mentioned variants of active loads are given below (calculated at typical points of the holes
for each of the mentioned variants of active loads are given below (calculated at typical points of the holes 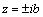 ;
; 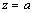 for
for 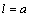 , where
, where 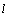 is the length of the aperture and also at the points
is the length of the aperture and also at the points 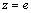 , for
, for 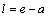 ).On the base of force action independence principle, by the superposition method we can determine stress state under simultaneous action of loads indicated in both cases:
).On the base of force action independence principle, by the superposition method we can determine stress state under simultaneous action of loads indicated in both cases: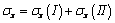 ;
;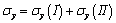 ;
;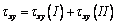
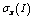 ,
, 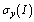 and
and 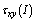 belong to the first,
belong to the first, 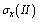 ,
, 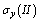 and
and 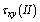 to the second problem.
to the second problem.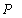 Acts on a Rectilinear Boundary
Acts on a Rectilinear Boundary 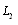 of a Weightless Half-Plane on the Segment
of a Weightless Half-Plane on the Segment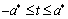
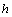 are the followings: (for typical points of the hole)Variant I:
are the followings: (for typical points of the hole)Variant I: 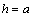 ;
; 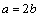 ;
;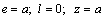 ; the point «
; the point «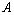 » in the draft
» in the draft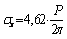 ;
; 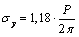
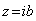 at the point «
at the point «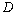 ».
».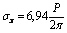 ;
; 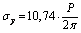 for
for 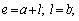 at the point
at the point 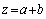 ;
;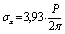 ;
; 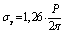 for
for 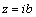 ;
;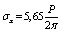 ;
; 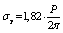 .for
.for 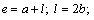 at the point
at the point 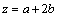 ;
;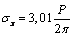 ;
;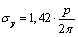 .Variant II:
.Variant II: 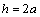 ;
; 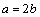 ;
; 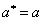 ;
;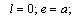 at the point
at the point 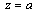 ;
; 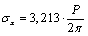 ;
; 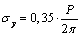 ; For
; For 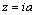 ;
; 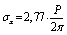 ;
; 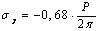 ;
; 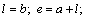 at the point
at the point 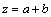 ;
; 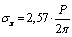 ;
; 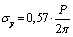 ;Variant III:
;Variant III: 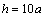 ;
; 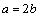 ;
; 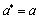
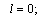 at the points
at the points 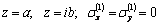 i.e. at considerable depths the additional stresses equal to zero (influence of a hole and load on a rectilinear boundary
i.e. at considerable depths the additional stresses equal to zero (influence of a hole and load on a rectilinear boundary 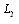 almost doesn’t influence the stress distribution).
almost doesn’t influence the stress distribution). (Ellipse with Two Rectilinear Cracks) is Subjected Only to the Action of Gravity
(Ellipse with Two Rectilinear Cracks) is Subjected Only to the Action of Gravity and
and 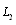 are free from external forces. Solving the system of equations for the right side in the form (3.12), we define the desired coefficients
are free from external forces. Solving the system of equations for the right side in the form (3.12), we define the desired coefficients 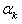 and
and 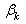 for different relative dimensions. Then, by formula (2.11) we find additional (as the result, total stresses) stresses:
for different relative dimensions. Then, by formula (2.11) we find additional (as the result, total stresses) stresses: 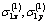 and
and 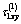 at the typical points of the hole
at the typical points of the hole 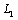 (since we are interested only in stress concentration at the points of hole’s contour). Below we give the found values of these stresses for different variants:Variant I:
(since we are interested only in stress concentration at the points of hole’s contour). Below we give the found values of these stresses for different variants:Variant I: 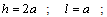
 for
for 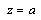 ;
; 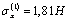 ;
;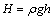 ;
; 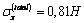 ;for
;for 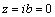 ;
; ;
;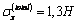 .Variant II:
.Variant II: 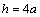 ;
;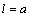 ;
;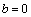 for
for 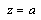 ;
; 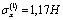 ;
; 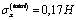 при
при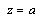 ;
; 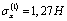 ;
; 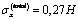 .Variant III:
.Variant III: 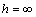 ;
; 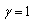 (distance piece factor equals to one), then at all the points of the contour
(distance piece factor equals to one), then at all the points of the contour 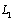 we have
we have 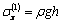 ;
;  .
.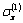 and total stresses on the
and total stresses on the 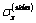 of a rectilinear aperture (i.e. at the end points of the crack and in the middle of this crack when
of a rectilinear aperture (i.e. at the end points of the crack and in the middle of this crack when 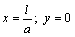 ) considerably increase when the crack of
) considerably increase when the crack of 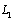 approaches to the linear contour
approaches to the linear contour 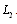 As calculations show, such type stresses have a particular local character and as a rule, they rapidly drop (weaken) when they are removed from the vertex of the crack, where they have maximal value. When
As calculations show, such type stresses have a particular local character and as a rule, they rapidly drop (weaken) when they are removed from the vertex of the crack, where they have maximal value. When 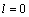 ,
, 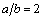 ;
; 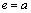 the internal contour
the internal contour 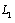 will become an ellipse, and the problem on definition of additional stresses will be similar to that in the paper[9]. Therefore, here we don’t cite the results.
will become an ellipse, and the problem on definition of additional stresses will be similar to that in the paper[9]. Therefore, here we don’t cite the results.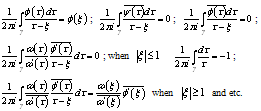
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML