-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Civil Engineering Research
p-ISSN: 2163-2316 e-ISSN: 2163-2340
2012; 2(1): 18-33
doi:10.5923/j.jce.20120201.04
Geometric Nonlinearity Effect on Seismic Behavior of High Arch Dams
A. Zeinizadeh, H. Mirzabozorg
Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran
Correspondence to: H. Mirzabozorg, Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this research, geometrically nonlinear dynamic analysis of arch concrete dam is attempted. At first, suitable models for large deformation analysis of massive plain concrete structures are investigated and by considering arch dam special features and properties, proper model for large displacement analysis is developed. A nonlinear analysis of the Dez arch dam using the engineering stress – strain model for large displacements is carried out under MCE ground motion. Fluid-Structure interaction is modeled including water compressibility and reservoir bottom absorption and the rock foundation is modeled as a mass-less flexible medium. Joint nonlinearity is also taken into consideration in the analysis. The penetration of water in opening joint during the earthquake is also considered and the significance of nonlinear geometry effects when accompanied by hydrodynamic pressure in joints is investigated. It is indicated that considering large deformation effects could be magnified when water penetration into opening joints is permitted. The obtained results showed that because the structural behavior of an arch dam does not allow large strains in a general manner, one can rule out the appearance of large displacements in the models including linear material.
Keywords: Arch Dams, Construction Joints, Geometric Nonlinearity, Water Penetration in Joints
Cite this paper: A. Zeinizadeh, H. Mirzabozorg, Geometric Nonlinearity Effect on Seismic Behavior of High Arch Dams, Journal of Civil Engineering Research, Vol. 2 No. 1, 2012, pp. 18-33. doi: 10.5923/j.jce.20120201.04.
Article Outline
1. Introduction
- The safety assessment of dams as costly infrastructures, the failure of which can jeopardize the lives of thousands and play havoc of the downstream land and facilities, is of grave importance. As a result, with many of the already built dams aging and on the other hand the need for new ones to be built, the number of studies conducted on concrete dams has increased significantly. One of the aspects that has always been important in analyzing high concrete structures, and recently has gained well-deserved attention in seismic evaluation of arch dams, is the issue of geometrically nonlinear behavior of these structures considering large displacements when subject to strong ground motions such as MCL earthquakes. This is of great importance not only in theory but also in practical applications. Considering the fact that dams are already built in almost all ideal locations, the engineers are left with no choice but to turn to other sites some of which have high seismicity or are even located on faults. Steno dam (Greece), Shirvan dam (Iran) and Klyde dam (New Zealand) are examples of such cases all of which need geometrically nonlinear analysis for realistic modeling of their behavior[1,2]. Earlier nonlinearstudies carried out on concrete arch dams’ structures can be classified into three groups:Nonlinear model of joints, including the contraction joints, construction joints and peripheral joints.Nonlinear model of mass concrete, including tensile cracking models, plastic models and damage mechanics models.Modeling geometric nonlinearity in the realm of large deformations.From the first category, studies conducted by Ahmadi et. al [3], Mays et. al[4], Lau et al[5], Hall[6], Ahmadi et. al[7] and Chuhan et. al[8] can be mentioned.Ahmadi et. al[3] presented a finite elements discrete crack modeling of the dams peripheral and vertical joints. In this study, only the tensile cracks resulting from persistent static loads were taken into consideration. They also developed a method for calculating the failure load which enables the safety analysis of the structures. Lau et al[4] studied the effect of linear and nonlinear behaviors on the magnitude of horizontal tensile stresses in arch dams. The nonlinear model featured three vertical contraction joints.It was observed that as the result of considering the contractions joints in nonlinear analysis, the tensile stress appearing near the joints in linear analysis is decreased. In this study only three contraction joints of the dam’s ten contraction joints were modeled. This is justified by the results obtained from the study conducted by Fenves et. al[9] indicating that modeling the three joint out of the several joints is enough for reaching the maximum tensile stress and as the number of modeled joints increase, the tensile stress changes from arch to cantilever form.In another study, Hall et. al[6] developed ADAP-88 software for smeared crack analysis of arch dam. ADAP-88 utilizes a multi-element discretization through the thickness of the dam to model the relative contact in the joints and cracks. Although using inter-element springs models the joints and cracks more realistically, smeared crack model was utilized in this study in favor of less computational cost and better convergence. The software assumes the reservoir water as incompressible. The foundation is mass-less which means there is no energy propagation toward the far end of the model.Ahmadi et. al[7] presented a discrete crack model of joints, for nonlinear dynamic analysis of concrete arch dam. A joint element model with a tensile-shear behavior was developed in order to analyze the dam-reservoir system more realistically. Chuhan et. al[8] investigated the non- seismic response of Xiaowan and Tujunga arch dams when featuring the contraction joints and reinforcements in joints. The model presented by Fenves et. al[9] (ADAP-88) was utilized for modeling the contraction joints. Factors such as the critical size of the elements, the number of contraction joints and the need for using reinforcement in joints were studied in this research. The reservoir was assumed to be incompressible, the joints behavior was linear-elastic and the foundation was mass less. It was shown that by opening the joint, the nature of the stresses transform from arch to cantilever, as a result the appearance of horizontal cracks in the dam becomes inevitable. In order to reduce the joint opening resulting in this kind of cracks, some steel reinforcement was provided in the model. From the second category we can refer to researches conducted by Olivier et. al[10], Faria et. al.[11], Lee et. Al [12], Feng et. al[13], Lotfi[14], Watanabe et. al[15] and Mirzabozorg et. al[16,17].Feng et al. [13] presented a method for stability analysis and crack propagation, based on linear-elastic crack mechanics and 3-D boundary element modeling. In another research by Lotfi et al.[14], a three-dimensional finite elements software was developed for studying the seismic response of arch dams. Non-orthogonal smeared crack approach and elasto-plastic material were implemented in the software modeling. Shahid Rajai dam in Iran was chosen as the case study. It was observed that in the smeared crack model and the elasto-plastic model, the dominant displacement is in the upstream and upward direction. Also it was shown that both smeared crack model and elasto-plastic model overcome defect the large value outputs of stress in linear analysis and give a more realistic prediction of stress distribution in the dam body. Watanabe et al.[15] used a three-dimensional curved surface isoparametric interface element for modeling vertical and peripheral joints. In this study both geometric nonlinearity and material nonlinearity are taken into consideration. For modeling the nonlinear behavior of concrete during loading and failure, a comprehensive elasto-plastic fracture stress-strain relationship, based on elasticity and plasticity theory was used. It was shown that during the earthquake, joint opening results in repeated redistribution of internal forces from arch to cantilever form and vice versa. This phenomenon eventually results in a stable state that is compatible with the real-life behavior of the dam.In another study by Mirzabozorg[17], a damage mechanics based approach was presented in which cracking occurred non-homogeneously in the elements; meaning that the crack in the elements propagated through Gaussian points. Marrow Point dam was chosen as the case study, for carrying out nonlinear analysis and the dam-reservoir interaction was also taken into account. Foundation was assumed to be rigid, while the reservoir was considered to be compressible and the reservoir bottom to have relative absorption. The proposed approach proved to have acceptable accuracy in predicting the crack propagation rout.From the third category researches conducted by Chang et al.[18], Youakim et al.[19], Khanloo et al.[20], Swaddiwudhipong et al.[21], Chin et al.[22], Polak et al.[23], Esmond[24], Sathurappan[25], Roca et al.[26], Bathe et al. [27] and Moradloo et al.[28] can be mentioned. Some of these nonlinear geometry studies were carried out on concrete dams and some on other concrete structures. Chang et al.[18] presented the nonlinear geometric seismic analysis of shell structures. Large displacements and large deformations were taken into account and Total Lagrangian approach was used with second Piola-Kirchhoff stress and Green- Lagrange strain. Material was taken as linear elastic and isotropic. Newton-Raphson iterative method accompanied by Newmark method was used for solving the equations. It was observed that in low natural frequencies, the behavior is dramatically affected by the seismic loading, whereas in high natural frequencies this sensitivity becomes less significant.Nonlinear analysis of tunnels with concrete lining bored into sandy soils was carried out by Youakim et al.[19]. The nonlinear behavior of the problem at hand originated from three sources; nonlinear material behavior of the concrete lining and the soil enclosing it, the effects of large deformations and the nonlinear nature of the sliding between concrete lining and the soil it is in contact with. It was assumed that stress-strain behavior of material is independent from temperature and time. Detail on the utilized formulation can be found in reference[29]. In another study, Khanloo et al.[20] modeled the nonlinear behavior of Tehran’s concrete communication tower. Cracking, crushing and large deformation effects were taken into consideration. Swaddiwudhipong et al.[21] presented a nine-node element for modeling the elasto-plastic large strain response of shell and plate structures using the Updated Lagrangian approach. Chin et al.[22] developed a thin plate element for geometrically nonlinear elastic analysis of thin wall structures. In this study the strains were assumed to be infinitesimal, and Updated Lagrangian approach was implemented.A methodology for analysis of nonlinear behavior of reinforced concrete shell structures was presented by Polak et al.[23]. Both geometrically nonlinear behavior and material nonlinearity were taken into consideration. Smeared rotating crack method was used for modeling crack propagation. Total Lagrangian approach along with Saint - Venant Kirchhof model was used for accounting for geometrically nonlinear behavior. In order to avoid shear-locking and zero-energy problems, selective integration was used.Esmond[24] conducted nonlinear geometric, material and time dependent analysis of reinforced concrete shell with edge beams. Geometric nonlinearity of the structure was assumed to stem from infinitesimal displacements and rotations. Concrete model was based on nonlinear elasticity with assumption of orthotropic material. Material nonlinearities include tensile cracking, tension stiffening between cracks, the nonlinear response of concrete in compression, and the yielding of the reinforcement are considered. Total Lagrangian approach along with Saint-Venant Kirchhof model was used for accounting for geometrically nonlinear behavior.Sathurappan et al.[25] performed the nonlinear analysis of reinforced and pre-stressed reinforced concrete slabs. Geometric nonlinearities and material nonlinearities were both considered in the study. Material nonlinearity of concrete was modeled by assuming plasticity in compression and cracking in tension. Total Lagrangian approach along with Saint-Venant Kirchhof model was used for accounting for geometrically nonlinear behavior.Numerical treatment of pre-stressing tendons in the analysis of reinforced concrete structures nonlinear behavior was investigated by Roca et al.[26]. Updated Lagrangian approach along with hypo-elastic model ofDarwinandPecknold was used for accounting for geometrically nonlinear behavior. Concrete material behavior in tension is assumed to be elasto-brittle.By presenting the characteristics of concrete used in ADINA software and some of its usages, Bathe et al.[27], suggested utilization of second Piola-Kirchhoff stress and Green-Lagrange strain (Saint-Venant Kirchhof model) for modeling large displacements in concrete structures.Moradloo et al.[28] used the Saint-Venant Kirchhof behavior model for large deformations to analyze the behavior of concrete arch dams during seismic excitation. The foundation was assumed to be rigid and the water-structure interaction was modeled by using the concept of added mass. For demonstrating the importance of large deformation effects, Marrow Point dam was analyzed using a nonlinear hyper-elastic model. Other sources nonlinearity such as joint opening and concrete material nonlinearity were ignored. Considering the characteristics of concrete such as not admitting large strains, Lagrangian approach along with Saint-Venant Kirchhof model was chosen for accounting for geometrically nonlinear behavior of non-reinforced concrete. It was shown that considering the effects of large deformations, can increase the displacement response of the dam crest by 11 percent in strong ground motions. Considering the characteristics of concrete arch dams it is expected that this increase in response become even more significant if the following features are also taken into account in the analysis:Water penetration effect in joints and cracksVertical and peripheral joints opening and sliding effectsAs it can be seen, in spite of the fact that several studies involving geometric nonlinear analysis of shells and plates structures have been carried out earlier[2], geometric nonlinear behavior of concrete dam has been given little attention in all the earlier researches. In the present study, co-rotational formulation for geometrically nonlinear analysis of concrete arch dams is presented. Using the presented formulation, nonlinear dynamic analysis of Dez arch dam under Manjil MCL earthquake is conducted to show large deformation effects. Foundation is assumed to be a mass-less flexible medium and Fluid- structure interaction is modeled including water compressibility and reservoir bottom absorption. Other source of nonlinearity in the analysis is joint opening. Concrete material nonlinearity is ignored. The penetration of water in opening joint during the earthquake is also considered and the significance of nonlinear geometry effects when accompanied by hydrodynamic pressure in joints is investigated.
2. Basic Concepts of Geometric Nonlinearity and Methodology Layout
- Structural nonlinearities may be caused by three main reasons, (a) material nonlinearities, (b) changing status, and (c) geometric nonlinearities. The key difference between the problems with geometric nonlinearity and other kinds of nonlinearity lies in the kinematics. The problems of geometric nonlinearity are usually dealt with, by tracing the geometrical changes in the structure and its elements with reference to a reference state, in an incremental manner. The increasing changes in the geometry of the structure due to proportionally growing applied forces may ultimately lead to elastic instability of the structure and its consequent failure. In this paper the effects of geometric nonlinearities on the seismic response of concrete arch dams is investigated. Generally there are two main distinct types of instability scenarios possible in geometrically nonlinear problems. These two kinds of instability behaviors depend closely on the concepts of limit point and bifurcation point on the load-displacement or equilibrium path of the structure. Description on these two mentioned types of structural instability behavior can be found in a number of papers published so far [e.g. 30,31] and hence is not elaborated on further, here.
2.1. Large Deformation Model
- A large deformation model consists of three main parts: A) Mesh Description and Governing equation, B) Constitutive Relation and C) Equation Linearization and solution algorithm.In a nonlinear analysis, the equilibrium of the body considered must be established in the current (deformed) configuration. Also it is necessary to employ an incremental formulation to confidentially describe the loading and the motion of the body. Also a suitable constitutive model is needed.In recent years, theoretical formulations and computational methods for dealing with geometric nonlinearities in the structures have been the focus of much attention[32-33]. In general, four approaches exist in kinematic modeling of geometrically nonlinear problems: Spatial or Eulerian Description, Material or Lagrangian, Arbitrary Eulerian- Lagrangian Description (AEL) and Co-rotational Description [28]. Each of these formulations can be useful for certain constitutive equation or loading conditions by decreasing the number of required transformations. In Eulerian approach the fact that the material and mesh movements are independent, poses difficulties in dealing with solid media when implementing the boundary conditions [28]. As a result, it is commonly used in fluid dynamics. In the Eulerian description large distortions in the motion of continuum can be dealt with more easily than Lagrangian approach, but generally at the expense of precise interface definition and resolution of flow details[34].ALE approach overcomes the shortcomings of purely Lagrangian and purely Eulerian descriptions. In the ALE description, nodes on boundary of initial mesh are fixed during deformation and nodes in the middle move such that element distortion will be minimized. In fact, the nodes of the computational mesh can be dragged along with the material particles as in Lagrangian approach, be held fixed similar to Eulerian manner, or be moved in some arbitrarily specified way to provide a continuous rezoning capability. Indeed by offering this freedom in moving the computational mesh, the ALE description retains the advantages of above- mentioned approaches while avoiding their disadvantages. Meaning that greater distortions of the continuum can be handled than that permitted in a purely Lagrangian method and with more resolution that what is allowed by a purely Eulerian approach.[28,34]The Lagrangian description is one of the most popular descriptions developed so far. In the Lagrangian approach a Cartesian coordinate system is employed to trace the structural deformation during loading history[28] that is, each material particle is followed by an individual node of the computational mesh associated with it, allowing easy tracking of free surfaces and boundaries between different materials. Also materials with history dependent constitutive relations are treated easily with Lagrangian approach [34] (arbitrary Lag-Eul methods). Depending on the way the deformations are described, the Lagrangian approach yields three main subgroups which are applicable in geometrically nonlinear analysis.Total Lagrangian Description (TLD) is the first type, in which the element’s original frame of reference is used to assess the deformations of the element and all the following element deformations are attributed to the same frame of reference and therefore the displacement variables involved in the derivation of element stiffness matrices in the former framework are the total instead of the incremental quantities [35]. In the total Lagrangian formulation the integrals in the weak form are carried out over the initial (reverence) configuration and derivatives are taken with respect to the material coordinates[28]. The ease of implementation is an advantage to this method. However, considering the fact that this method is unable to tell apart the rigid body motion of the element from its local deformation, this defect results in incorrect description of the equilibrium path, unless the rotations and deflections in the problem are small[32].Updated Lagrangian Description (ULD) is the second type. In this method the current configuration is taken as the reference frame for the following step and by doing so the inability of TLD in distinguishing the rigid body motions from local deformation is overcome. In the update Lagrangian formulation, the derivatives are obtained with respect to the spatial coordinates; the weak form involves integrals over the deformed (or current) configuration. This method yields a more precise description of the displacement field of elements and the structure. In UL formulation there is no need to calculate initial stiffness in each iteration. Also in using UL formulation the artificial straining does not occur [35]. However, the calculation of the local element deformation during each stage of loading proves to be laborious. In addition, when it comes to developing a consistent set of equilibrium equations for incremental analysis, the transformation of the tangent stiffness matrix from local to global axes calls for a great deal of matrix operations [36]. As a result this type of description of displacement has not become much appealing in practical structural applications unless, the problem is of elastic nature and involves very large defections.Partially Updated Lagrangian Description (PULD), as the third derivation of the Lagrangian approach, utilizes the idea of the rigid-convected coordinates’ method as in ULD formulation. In this approach the coordinates of each element is are updated only once at the start of each loadstep then the numerical operations within each loadstep are then carried out as in TLD approach. This type of formulation has both of the advantages of the simplicity in TLD formulation and the accuracy in ULD formulation at the same time. Interested reader is referred to[37-39] for more detail on this type of formulation.In concrete dam analyses, since small strain, element large distortion is not occurs and if initial finite element mesh well designed there is no anxiety about distortion and following precise reduction in results. Geometric nonlinear of arch concrete dam is a nonlinear problem with large displacement and small strain. With respect to stage construction of arch concrete dam and concrete purities itself it expected that under severe earthquake loading, dam monoliths experienced large slip and large deformation caused by joint opening and failure with amount of crushing and plastic deformations.The description utilized in the current study is the co-rotational (CR) approach. This approach is identical to PULD except for the fact that in the former, the element coordinate systems are rotating during the time steps. In Co-rotational approach initial configuration consists of two parts, stresses and strain calculated from rotated configuration and rigid body motion deduced from initial configuration. In this method the FEM equations of each element are attributed to two systems (as shown in figure 1):A fixed or base configuration CB as in TLD.A co-rotated configuration that is dragged along with the element an in fact is a rigid body motion of CB. This is fairly similar to ULD.
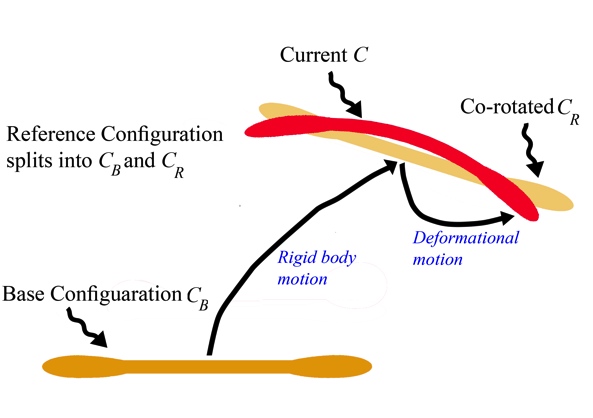 | Figure 1. The CR kinematic description; “Current configuration” means any one assumed by the body or element during the analysis process. It is not necessarily an equilibrium configuration[35] |
2.2. Implementation of Corotational Approach
- The strain-displacement nonlinearity in the CR approach is described as[49],
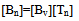 | (1) |
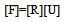 | (2) |
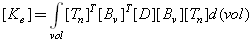 | (3) |
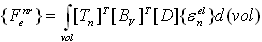 | (4) |
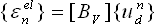 | (5) |
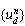 describes the element deformation, which causes the strain to appear. For each element the large rotation approach can be described in three steps:1. The element updated transformation matrix [Tn] is calculated2. The deformational displacement
describes the element deformation, which causes the strain to appear. For each element the large rotation approach can be described in three steps:1. The element updated transformation matrix [Tn] is calculated2. The deformational displacement 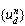 is obtained from the total displacement {un} in order to calculate the restoring force
is obtained from the total displacement {un} in order to calculate the restoring force 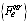 and the stresses.3. Node rotations are updated according to the computed rotational increments in
and the stresses.3. Node rotations are updated according to the computed rotational increments in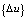 .Effective implementation of the three steps above requires the concept of a rotational pseudo-vector[].
.Effective implementation of the three steps above requires the concept of a rotational pseudo-vector[].2.2.1. Element Transformation
- As mentioned earlier, the updated transformation matrix [Tn] transforms the current element coordinate frame to the global Cartesian coordinate system (see Figure 2).
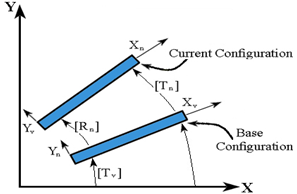 | Figure 2. Element Transformation Definitions[49] |
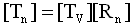 | (6) |
2.2.2. Deformational Displacement
- The displacement an element undergoes can be decomposed into a rigid body translation, a rigid body motion, and a components that causes the strain,
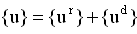 | (7) |
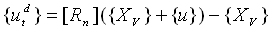 | (8) |
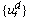 = translational component of the deformational displacement[Rn] = current element rotation matrix{xv} = Original element coordinates in the global coordinate system{u} = Element displacement vector in global coordinates{ud} is in the global coordinate system. The rotational components of DOFs are calculated by subtracting the nodal rotations {u} from the element rotation {ur}. This operation is performed as follows for each node (utilizing the pseudo-vectors): 1. A transformation matrix from the nodal pseudo-vector {θn} is calculated, yielding [Tn]. 2. The relative rotation [Td] between [Rn] and [Tn] is computed:
= translational component of the deformational displacement[Rn] = current element rotation matrix{xv} = Original element coordinates in the global coordinate system{u} = Element displacement vector in global coordinates{ud} is in the global coordinate system. The rotational components of DOFs are calculated by subtracting the nodal rotations {u} from the element rotation {ur}. This operation is performed as follows for each node (utilizing the pseudo-vectors): 1. A transformation matrix from the nodal pseudo-vector {θn} is calculated, yielding [Tn]. 2. The relative rotation [Td] between [Rn] and [Tn] is computed: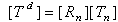 | (9) |
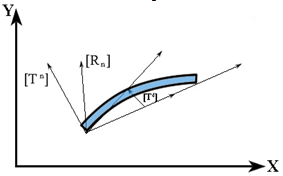 | Figure 3. Definition of Deformational Rotations[49] |
2.2.3. Updating Rotations
- After obtaining the transformation [T] and deformational displacements {ud}, the element matrices and restoring force can be calculated from equations (3) and (4), respectively. A displacement increment {Δu} results from the solution of the system of equations. The rotational components of {Δu} are used to update the nodal rotations at the element level. The global rotations are updated simply by adding to the previous rotation in {un-1} and by the pseudo-vector approach.
2.2.4. Consistent Tangent Stiffness Matrix and Finite Rotation
- The use of consistent tangent stiffness in a nonlinear analysis can speed up the convergence trend to a quadratic rate of convergence. A consistent tangent stiffness matrix is derived from the discretized finite element equilibrium equations without the introduction of various approximations. The process of deriving of the consistent tangent stiffness matrix used for the corotational approach is outlined below [49,50].For each element, the nonlinear static finite element equations solved are defined as:
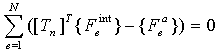 | (10) |
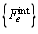 = element internal force vector in the element coordinate system,
= element internal force vector in the element coordinate system,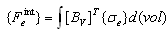 | (11) |
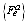 = Applied load vector at the element level in the global coordinate systemNow we derive the consistent tangent matrix at the element level without introducing an approximation. The consistent tangent matrix is obtained by differentiating equation (10) with respect to displacement variables {ue}:
= Applied load vector at the element level in the global coordinate systemNow we derive the consistent tangent matrix at the element level without introducing an approximation. The consistent tangent matrix is obtained by differentiating equation (10) with respect to displacement variables {ue}: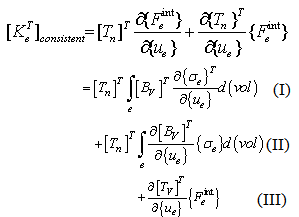 | (12) |
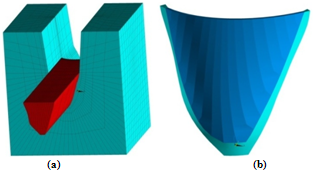 | Figure 4. (a) Dam-Reservoir-Foundation finite element model and (b) Dam body and the concrete saddle |
3. Numerical Model of a Typical High Arch Dam
- Dez double curvature arch dam in Iran is selected as the case study. Crest length is 240m and thickness at the crest level is 4.5m (Figure 4). Finite element idealization prepared for the dam, foundation rock and reservoir is shown in Figure 4a, which consists of 792 solid elements for modeling the dam body and its concrete saddle, 3770 solid elements for simulation of the foundation rock and 3660 fluid elements in the reservoir domain. In addition, 956 node-to-node contact elements are used to model vertical and peripheral joints of the dam. Figure 5 shows the surfaces on which the contact elements are located.
 | Figure 5. Vertical and peripheral joints in DEZ dam |
3.1. Basic Mechanical and Strength Parameters
- Water is assumed to be compressible with density of 1000kg/m3. The speed of sound in water is 1440m/s and the wave reflection coefficient at the boundaries of the reservoir with the abutments and at its bottom is taken to be 0.8, conservatively. A viscous boundary at the far end of the reservoir dissipates the waves reaching this boundary and prevents them from being reflected back into the reservoir. Having neglected the sloshing effects, we have imposed zero pressure boundary condition for reservoir free surface. This assumption is acceptable for high dams[52,53]. Table 1 shows the material properties for the mass concrete and the foundation of the model[54,55]
3.2. Loading
- The loads applied to the model in chronological order are, self-weight of the dam body (during 10 stages of construction and sequential joint grouting), hydrostatic pressure (considering gradual impoundment), thermal loading (summer condition, obtained from transient thermal analysis of the dam including solar radiation phenomenon [55]) and finally the seismic excitation. The coupled nonlinear dam-reservoir-foundation system problem is solved employing the β-Newmark time-integration method. For dynamic analysis, the system is excited in maximum credible level using Manjil earthquake scaled based on response spectrum of the dam site. Table 2 presents the characteristics of Manjil ground motion.
| |||||||||||||||
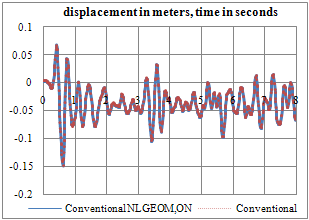 | Figure 6. Upstream-Downstream displacement time-history of crown cantilever at crest level (Conventional analysis) |
4. Results and Discussion
4.1. Crest Displacement
- Figures 6 to 8 compare the crest displacement in the three principal directions for the two cases of with and without geometric nonlinearity. In addition, Table 3 represents briefly the extreme values resulted from the conducted analyses. As can be seen, when hydrodynamic pressure is applied in the open joints, geometric nonlinearity can lead to about 5% increase in upstream-downstream extreme displacement. The corresponding values for transvers and vertical directions are 7.5% and 1.4%, respectively.
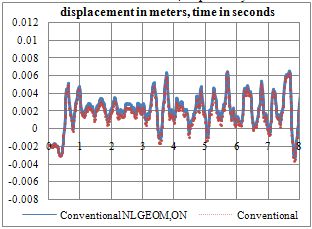 | Figure 7. Transverse displacement time-history of crown cantilever at crest level (Conventional analysis) |
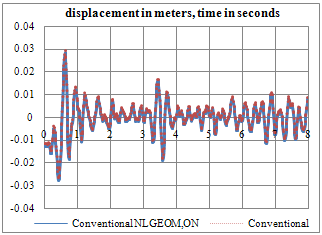 | Figure 8. Vertical displacement time-history of crown cantilever at crest level (Conventional analysis) |
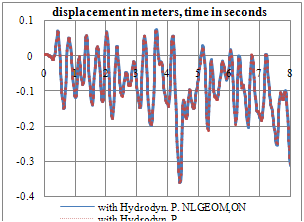 | Figure 9. Upstream-Downstream displacement time-history of crown cantilever at crest level (with Hydrodynamic pore-pressure in joints) |
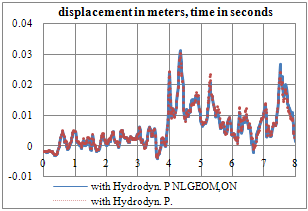 | Figure 10. Transverse displacement time-history of crown cantilever at crest level (with Hydrodynamic pore-pressure in joints) |
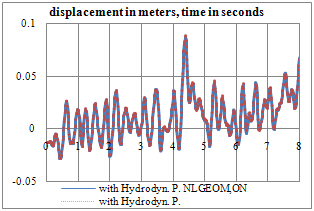 | Figure 11. Vertical displacement time-history of crown cantilever at crest level (with Hydrodynamic pore-pressure in joints) |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
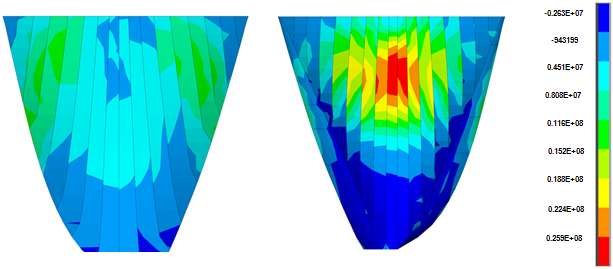 | Figure 12. Non-coincident push of 1st principle stress in analysis with hydrodynamic pressure in joints, by loadstep 400 (second 8) |
4.2. Stress Distribution
- Figures 12 and 13 show the non-coincident envelope of the first and third principal stresses when water can penetrate into open joints and Figure 14 and 15 show the corresponding envelopes when geometric nonlinearity is accounted for. Table 4 represents briefly the extreme values of the principal stresses for various cases. Based on the shown envelopes and the table, the effect of geometric nonlinearity is negligible so that there is not any change in maximum tensile stress and the maximum compressive stress increases just about 4.7%.Figures 16 and 17 show the envelopes pertinent to the non-coincident principal stresses when there is no water penetration in open joint and Figures 18 and 19 represent the corresponding stress envelopes when geometric nonlinearity is taken into consideration in the conducted analysis and finally, Table 4 represents the results briefly. As expected, when water penetration is not permitted, the effect of geometric nonlinearity is almost imperceptible.
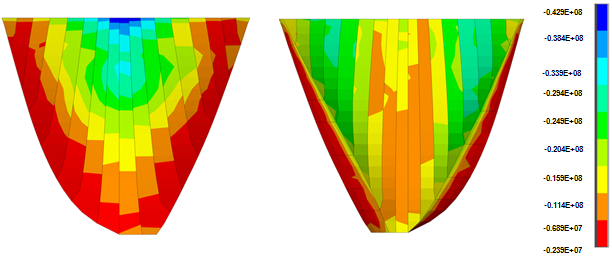 | Figure 13. Non-coincident push of 3rd principle stress in analysis with hydrodynamic pressure in joints, at loadstep 400 (second 8) |
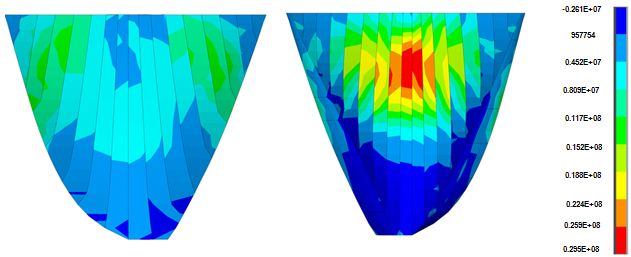 | Figure 14. Non-coincident push of 1st principle stress in analysis with hydrodynamic pressure in joints, by loadstep 400 (second 8) with geometric nonlinearity effects |
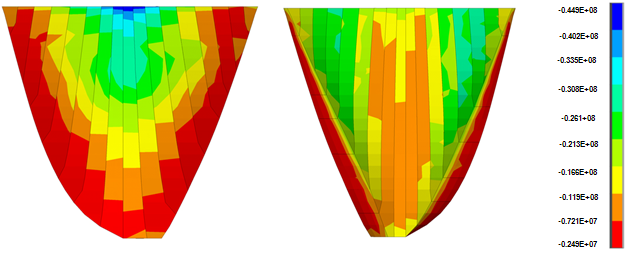 | Figure 15. Non-coincident push of 3rd principle stress in analysis with hydrodynamic pressure in joints, at loadstep 400 (second 8) with geometric nonlinearity effects |
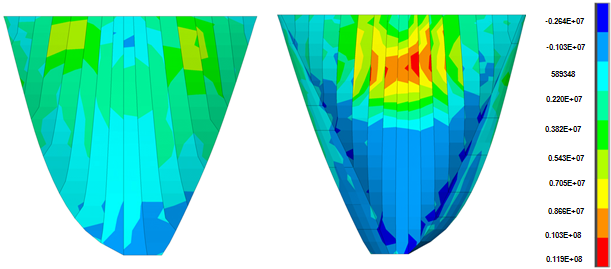 | Figure 16. Non-coincident push of 1st principle stress in conventional analysis, by loadstep 400 (second 8) |
 | Figure 17. Non-coincident push of 3rd principle stress in conventional analysis, at loadstep 400 (second 8) |
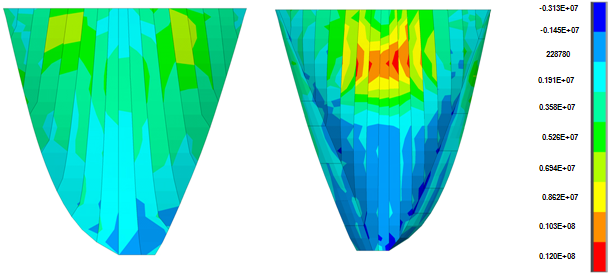 | Figure 18. Non-coincident push of 1st principle stress in conventional analysis, by loadstep 400 (second 8) with geometric nonlinearity effects |
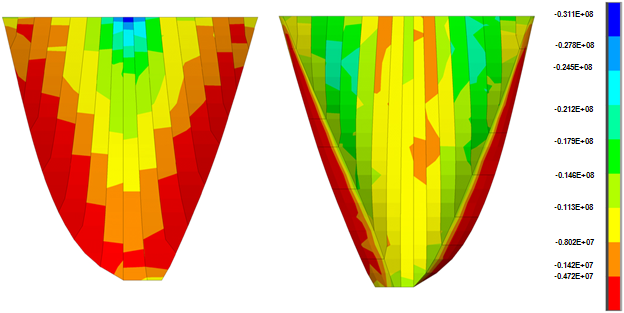 | Figure 19. Non-coincident push of 3rd principle stress in conventional analysis, at loadstep 400 (second 8) with geometric nonlinearity effects |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
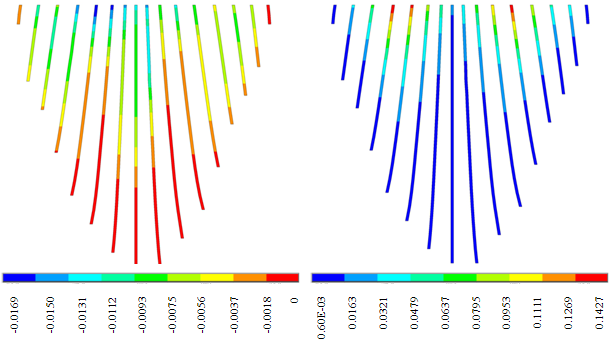 | Figure 20. Non-coincident push of joint openings (Gap on the left & Sliding on the right) in analysis with hydrodynamic pressure in joints, by loadstep 400 (second 8) |
4.3. Joint Opening/Sliding
- Figure 20 shows the non-coincident envelope of the joints’ opening and sliding when water can penetrate into open joints and Figure 21 shows the corresponding envelopes when geometric nonlinearity is accounted for. Table 5 briefly represents the extreme values of the joint responses for various cases. Based on the shown envelopes and the table, it can be seen that when hydrodynamic pressure is applied in the open joints, the effect of geometric nonlinearity on joint opening is negligible. Figures 22 shows the envelope of the joints’ opening and sliding when there is no water penetration in open joints and Figure 23 represents the corresponding opening envelopes when geometric nonlinearity is taken into consideration in the conducted analysis and finally, Table 5 summarizes the results briefly. When water penetration is not permitted, the joints’ sliding is decreased by 3.6% due to geometric nonlinearity and there is no noticeable change in joint opening.
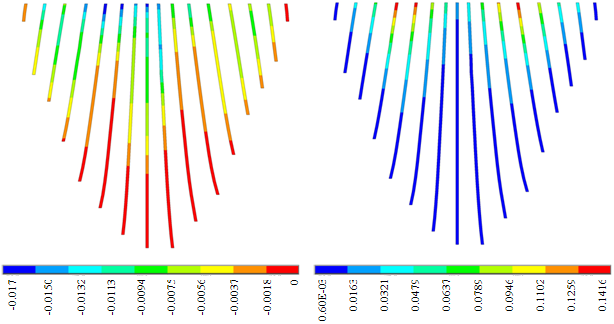 | Figure 21. Non-coincident push of joint openings (Gap on the left & Sliding on the right) in analysis with hydrodynamic pressure in joints, by loadstep 400 |
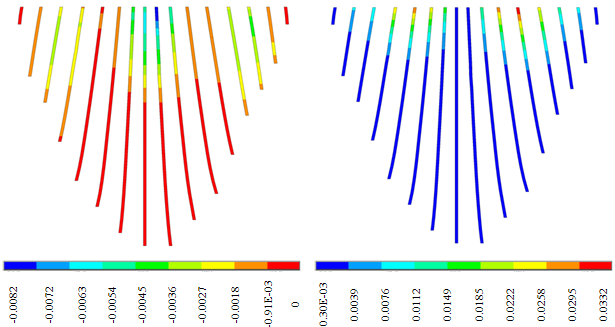 | Figure 22. Non-coincident push of joint openings (Gap on the left & Sliding on the right) in conventional analysis, at loadstep 400 (second 8) |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.4. Discussion
- In the previous sections, the results obtained from four nonlinear analyses considering construction joints effects were presented. The analyses were different from the point of considering the effects of geometric nonlinearity including/excluding water penetration into open joints. Based on the presented results, geometric nonlinearity effect on the structural behavior is magnified when water penetration is permitted. However, this effect is negligible. The insignificant effect of geometric nonlinearity on the dam behavior is justifiable by the fact that the nonlinear material behavior of mass concrete was excluded in the present study. Considering the fact that one of the main sources of nonlinear behavior in MCL condition is material nonlinearity in tensile and compressive states in mass concrete and taking it into account, increases the displacement response of the dam, it is predicted that geometric nonlinearity will have a more noticeable effect on the dam response. This case is the subject of the future study by the authors.
5. Conclusions
- In the present paper the effects of nonlinear geometry on the seismic response of a real-life high arch dam model was investigated. Co-rotational approach was utilized for formulating the large-deformation phenomenon. The behavior of mass concrete was assumed to be linear while all of the construction and peripheral joints were modeled according to as-built construction details. The reservoir water was assumed to be compressible and the foundation rock was modeled as a mass-less medium. It was observed that when water penetration in opening joints of the dam is permitted during the excitation, the response of the dam increases, nevertheless this increase in the dam response is insignificant. According to authors experience and engineering judgment, it is predicted that considering the material nonlinearity will magnify the effects of geometric nonlinearity.
References
| [1] | NRC, “Earthquake Engineering for Concrete Dams: Design, Performance, and Research needs”National Research Council, 1990 |
| [2] | J. Moradloo, “Nonlinear dynamic analysis of archconcretedam considering larged is placements”PhD Thesis, Department of Civil engineering, TMU, 2007 |
| [3] | M.T. Ahmadi, S. Razavi, “A three dimensional joint opening analysis of an arch dam”, Computers, Structures, Vol,44, No.1/2, PP.187-192,1992 |
| [4] | J.R. Mays, L.H. Roehm, “ Effect of vertical contraction joints in concrete arch dams”, Computers, Structures, Vol7, NO.4/5, PP.615-627, 1993 |
| [5] | D.T. Lau, B. Noruziaan, G. Razaqpur, “Modeling of contraction joint and shear sliding effects on earthquake response of arch dams”, Earthquake Engineering and Structural Dynamics,27,PP.1013-1029, 1998 |
| [6] | J.F. Hall, “ Efficient nonlinear seismic analysis of arch dams”, Earthquake Engineering and Structural Dynamics,27,,PP.1425-1444, 1998 |
| [7] | M.T. Ahmadi, M. Izadinia, H. Bachmann,” A discrete crack joint model for nonlinear dynamic analysis of concrete arch dam”, Computers, Structures, 79, PP.403-420, 2001 |
| [8] | Z. Chuhan, X.Yanjie, W. Guanglun, J. Feng, “ Nonlinear seismic response of arch dams with contraction joint opening and joint reinforcements” Earthquake Engineering, Structural Dynamics, 29, 1547-1566, 2000 |
| [9] | G. L. Fenves, S. Mojtahedi, R. B. Reimer," ADAP-88: A computer program for nonlinear earthquake analysis of concrete arch dams”. Report No.EERC 89-12, Earthquake Engineering Research Center,University of California, Berkeley, CA, 1989 |
| [10] | J. Olivier, M. Cevera, “ Seismic evaluation of concrete dams via continuum damage models”,Earthquake Engineering and Structural Dynamics, Vol.24, PP.1225-1245, 1995 |
| [11] | R. Faria, J. Oliver, M. Cevera, “ A strain-based plastic viscose damage model for massive concrete structures”, International Journal of Solids Structures, Vol.35, No.14, pp.1533-1558,1998 |
| [12] | J. Lee , G. L. Fenves, “A plastic– damage concrete model for earthquake analysis of dams”, Earthquake Engineering and Structural Dynamics,27,pp.937-965, 1998 |
| [13] | L. M. Feng, O. A. Pekauo, “Cracking analysis of arch dams by 3D boundary element method”, Journal Of Structural Engineering Vol.122, No.6, 1996 |
| [14] | V. Lotfi, R. Espandar, “Comparison of non-orthogonal smeared crack and plasticity models for dynamic analysis of concrete arch dams”, Computers, Structures, Vol.81, Issue 14, pp 1461-1474, 2003 |
| [15] | H. Watanabe, S. Razavi, “Effect of joint opening and material nonlinearity on the seismic response of concrete arch dam”, 12,th World Conference of Earthquake Engineering, 2000 |
| [16] | H. Mirzabozorg, “Damage mechanics approach in seismic analysis of concrete gravity dams including dam-reservoir interaction”, European earthquake engineering 3, 2004 |
| [17] | H. Mirzabozorg, “Non-Linear behavior of mass concrete in three-dimensional problems using a smeared crack approach”, Earthquake Engineering and structural Dynamics 34 : 247-269, 2005 |
| [18] | T. P. Chang, H. C. Chang, “ Nonlinear vibration analysis of geometrically nonlinear shell structures”, Mechanics Research Communication,Vol.27, No.2, pp.173-180, 2000 |
| [19] | S. A. S. Youakim, S. E. E. El-metewally, W. F. Chen, “Nonlinear analysis of tunnels in clayey/sandy soil with a concrete lining”, Engineering Structures, 22,PP.707-722, 2000 |
| [20] | A. R. Khaloo, N. Asadpour, A. M. Horr, “Full dynamic analysis of Tehran tele-communication tower, linear and nonlinear responses”, The Structural Design of Tall Building,10, 263-281, 2001 |
| [21] | S. Swaddiwudhipong, Z. S. Liu, “Dynamic Response of Large Strain Elastic_Plastic Plate and Shell Structures”, Thin-Walled Structures, Vol.26, No.4,1 996, PP.223- 239. |
| [22] | C. K. Chin, F. G. A. Al-bermani, S. Kitiporvchai, “Nonlinear Analysis of Thin –Walled Sructures Using Plate Elements”, International journal for numericak method in engineering, Vol.37, PP.1697-171, 1994 |
| [23] | M. A. Polak, F. J. Vecchio, “Nonlinear analysis of reinforced concrete shells”, Journal of Structural engineering, Vol.119, No.12, December, 1993 |
| [24] | C. Esmond, “Nonlinear Geometric, Material and time dependent analysis of reinforced concrete shell with edge beams”, Report No UCB/SESM 82/08, Department of civil engineering university of California Berkeley, California, 1982 |
| [25] | G. Sathurappan, N. Rajagoplan, C. S. Krishnamoorthy, “Nonlinear Finite element analysis of reinforced and prestressed concrete slabs with reinforcement (inclusive of prestressing steel ) modeled as discrete integral components”, Computers and Structures, Vol.44, No.3, 1992,pp.575-584, 1992 |
| [26] | P. Roca, A. R. Marti, “Numerical treatment of prestressing tendons in numerical analysis of prestressed concrete structures I”, Computers and Structures Vol.46, No.5,PP. 905-916, 1993 |
| [27] | K. J. Bathe, J. Walczak, A. Welch, N. Mistry, “ Nonlinear analysis of concrete structures”, Computers and Structures,Vol.32,pp.563-590, 1989 |
| [28] | J. Moradloo, M.T. Ahmadi, Sh. Vahdani “Nonlinear Dynamic Analysis of Concrete Arch Dam Considering Large Displacements”. The 14th World Conference on Earthquake Engineering, Beijing, China, 2008 |
| [29] | K. J. Bathe, “Finite Element Procedures”, Prentice-Hall, Inc., 1996 |
| [30] | E. Riks, “The application of Newton’s method to the problem of elastic stability”. J. Appl. Mech., Trans. ASME 72-APM-P, 1060-1065, 1972 |
| [31] | P. G. Bergan, “Solution algorithms for nonlinear structural problems”. Comout. Struct. 12. 497-509, 1980 |
| [32] | K. Mattiasson, A. Bengtsson, A. Samuelsson, “On the accuracy and efficiency of numerical algorithms for geometrically nonlinear structural analysis”. In Proc. Finite Element Methods for Nonlinear Problems, Europe-US. Symp., Trondheim, pp. 3-23, 1985 |
| [33] | R. Szilard, “Critical load and post-buckling analysis by FEM using energy balancing technique”. Compur. Struct. 20, 277-286, 1985 |
| [34] | J. Donea, A. Huerta, J. Ph. Ponthot, A. Rodr´ıguez-Ferran, “Arbitrary Lagrangian-Eulerian methods”, Encyclopedia of Computational Mechanics. John Wiley & Sons, Ltd., 2004 |
| [35] | C. A. Felippa, “A Symmetric Approach to The Element-Independent Co-Rotational Dynamics of Finite Elements”, CU-CAS-00-03 Center of Aerospace Structures, 2000 |
| [36] | G. H. Powell, “Theory of nonlinear elastic structures”. J. Struct. Div., ASCE 95, 2687-2701, 1969 |
| [37] | P. Jetteur, S. Cescotto, V. deGoyet, “Improved nonlinear finite elements for oriented bodies using an extension of Marguerre’s theory”. Comput. Struct. 17, 129-137, 1983 |
| [38] | R. K. Wen and J. Rahimzadeh, “Nonlinear elastic frame analysis by finite element”. J. Struct. Engng, ASCE 109, 1952-1971, 1983 |
| [39] | A. Peterson and H. Petersson, “On finite element analysis of geometrically nonlinear problems”. Comput. Meth. appl. Mech. Engng 51, 277-286, 1985 |
| [40] | A. Chajes, J. E.Churchill, “Nonlinear frame analysis by finite element method”. Journal of Structural Engineering; 113:1221–35, 1987 |
| [41] | K. Mattiasson, A. Bengtsson, A. Samuelsson, “On the accuracy and efficiency of numerical algorithms for geometrically nonlinear structural analysis”. Finite element methods for nonlinear problems, Berlin: Springer, 1986:3–23 |
| [42] | K.J. Bathe, S. Bolourchi, “Large displacement analysis of three-dimensional beam structures”, Inter- national Journal for Numerical Methods in Engineering 1979;14:961–86 |
| [43] | M. Gattass, J. F. Abel, “Equilibrium considerations of the Updated Lagrangian formulation of beam-columns with natural concepts” International Journal for Numerical Methods in Engineering 1987;24:2119–41 |
| [44] | H. Chen, G. E. Blandford, “Thin-walled space frames. I: Large deformation analysis theory”, Journal of Structural Engineering 1991;117:2499–520 |
| [45] | A. F. Saleeb, T. Y. P. Chang, A. S. Gendy, “Effective modeling of spatial buckling of beam assemblages, accounting for warping constraints and rotation-dependency of moments”. International Journal for Numerical Methods in Engineering 1992;33:469–502 |
| [46] | Y. B. Yang, L. J. Leu, “Non-linear stiffnesses in analysis of planar frames”. Computer Methods in Applied Mechanics and Engineering 1994;117:233–47 |
| [47] | L. H. Teh, M. J. Clarke, “Co-rotational and Lagrangian formulations for elastic three-dimensional beam finite elements”. Elsevier Journal ofConstructional SteelResearch48,1998: 123–144 |
| [48] | G. Garcea, A. Madeo, R. Casaciaro, “The Implicit Corotational Method: a tool for obtaining geometrically nonlinear models for fibred continua”.Dipartimento di Modellistica per l'Ingegneriauniversità della Calabria |
| [49] | ANSYS11 “Theory manuals”,2005 |
| [50] | B. Nour-Omid, C. C. Rankin, "Finite Rotation Analysis and Consistent Linearization Using Projectors", Computer Methods in Applied Mechanics and Engineering, Vol. 93, pp. 353-384, 1991 |
| [51] | J. Argyris, "An Excursion into Large Rotations", Computer Methods in Applied Mechanics and Engineering, Vol. 32, pp. 85-155, 1982 |
| [52] | F. Javanmardi, P. Léger, R. Tinawi, “Seismic water pressure in cracked concrete gravity dams: experimental study and theoretical modeling.” Submitted to Journal of Structural Engineering ASCE, 2003 |
| [53] | H. W. Reinhardt, M. Sosoro, X. Zhu, ‘‘Cracked and repaired concrete subject to fluid penetration.’’Mat. andStruct., Paris, 31,1998, 74–93 |
| [54] | F. Javanmardi, “Transient uplift pressures in seismic cracks induced in concrete dams: shake table experiments, theoretical modeling, and case study.” Ph.D. Thesis, Department of Civil Engineering, École Polytechnique de Montréal. Montreal, Canada, 2003. |
| [55] | M.A. Hariri Ardebili, H. Mirzabozorg , M. Ghaemian, M. Akhavan, R. Amini, “Calibration of 3D FE model of DEZ high arch dam in thermal and static conditions using instruments and site observation”, 6th International Conference in Dam Engineering, Lisbon, Portugal, Feb2011 |
| [56] | M.D. Trifunac, A.G. Brady. “A study of the duration of strong earthquake ground motion”, Bull. Seismology. Soc. Am. 65, 1975: 581-626. |
| [57] | M. A. Hariri Ardebili, H. Mirzabozorg, M. Akbari, F. Danesh, “Effects of near-fault ground motions in seismic performance evaluation of a symmetry arch dam on rigid and mass-less foundations”, 6th International Conference of Seismology and Earthquake Engineering, 16-18 May 2011 Tehran, Iran |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML