1. Introduction

Many bridges and other structures built during the post-war reconstruction period are finishing their useful life and present a growing risk from cumulative damage. Growing costs of renewing infrastructure built during the high economic growth period have been recognized since the 1990s. Central government agencies and autonomous bodies have begun discussing asset management of this infrastructure since the first half of the 2000s [1].

Shortage of human resources to manage the huge amount of infrastructure properly is a daunting issue because of aging technicians and increasing scarcity of younger workers in our society, caused by an increasingly low birth rate and increasing longevity. It has become gradually even more difficult to maintain, repair, and renew infrastructure after finding areas of degradation and checking the conditions for conserving them. The Ministry of Land, Infrastructure, Transport and Tourism reported that 121 road bridges were close to collapsing because of concrete deterioration and steel member corrosion as of April, 2008 [2], [3]. Recently in December 2, 2012 in a tunnel on the Tokyo bound Chuo highway, 270 pieces of concrete plate (5×1.2 × 0.09 m, around 1.2 t) attached to the tunnel ceiling fell to a road surface at a point about 1700 m from an exit to Ohtsuki City. They were folded in a V-shape, forming a debris field that was some 110 m long. Three vehicles heading to Tokyo were buried under the debris and caught fire, killing nine people [4].

Catastrophic disasters of this type would have been avoided if adequate safety measures such as establishing examination routines and setting laying sensors had been taken. Figure 1 presents bridge damage in Japan and in the USA.

Figure 1. Old damaged bridge and maintenance examples in Japan and the USA

Although bridges and other structures are presumably visually inspected periodically, at five-year intervals, finding anomalies that can develop rapidly between successive inspections is reportedly difficult, especially in light of a shortage of qualified personnel and reduced budgets for inspection. The existence of many places that are visually checked only slightly during periodical examinations exacerbates the situation. In times of disaster recovery, quick safety evaluation must be performed, but such emergency inspections usually take a considerable amount of time, which would retard the process of disaster recovery. Therefore, much work remains to be done in this field [5]. If a major disaster should strike in the days ahead, then large and numerous accidents might occur easily, cutting commercial arteries, stall national and regional economies, and kill many people. Appropriate actions must be taken quickly.

For this study, the authors developed a simple monitoring system to measure the natural frequency from vertical vibration waves detected on the plate deck of support pillars and beams subjected to deflection and vibration.

We conducted this research to meet the great demands of practical measurement technologies to diagnose the soundness of infrastructure after a major disaster or during the aging process. Our system sensors can detect signals when attached to a vibrating surface, as when a stethoscope is placed on the skin. Our system, which can measure a natural frequency and other phenomena using a simple procedure, has a practical structure, moderate cost, and ease of use. These are outstanding features of our system that contrast against conventionally used systems, which have high-accuracy but also high cost.

In addition, our system eliminates the need for a power supply for the sensor because it makes use of the electromotive force of the piezoelectric effect.

A monitoring system meeting the Ministry of Land, Infrastructure, Transport and Tourism requirements must have some important features: (1) Data obtained using the system must be readily comparable to prior inspection results. (2) The system must be universally applicable to any site to work effectively. (3) The system must show any infrastructural changes after a disaster such as an earthquake. (4) The system must reduce costs of maintenance and be labor-saving [5]. Figure 2. presents bridge for measurement.

Figure 2. Target bridge for measurements (Asuka Ohashi Bridge). The bridge comprises seven spans having total length of 256 m. Experimental measurements were taken of the first span near the left abutment

2. Measurements of Vibration and Displacement in the Floor Slabs of Bridges in Service

2.1. Comparison with Conventional Technologies

To detect small displacements and vibrations of bridges, people have made use of measuring devices that offer high accuracy and high resolution [6-12]. They used accelerometer, laser displacement sensor, and strain measurements with optical fibre and attained 5 µm accuracy [13].

A few reports have described structural health monitoring systems making use of piezoelectric cable as a simple method of measurement. In one system, piezoelectric cable was inserted into the center of iron bolt available commercially and was sealed using adhesive. Then the terminal leads were connected to a logger that measured the change of output voltage. The bolt was set in a joint hole of a structure. Then the nut was fastened using the same tightening torque with that of the structural bolt–nut. They measured the shearing stress in the axial direction of the bolt and stress in the bolt [14].

In another example, investigators buried piezoelectric cable along the entire length of a reinforced concrete slab to sense crack generation occurring within it. That sensor can detect the bending moment loaded on the slab [15]. Because both sensors were directly subjected to forces exerted to the joint bolt (first example) or the concrete slab (second example), they were deformed by fatigue or could be broken. Consequently, these methods might not be applied to long-term smart sensing. In addition, the difficult problem of noise separation associated with these methods caused by generation of a tiny signal corresponding to very small deformation. The S/N ratio brings about a tricky issue.

2.2. Outline of Bridge

Asuka Ohashi Bridge, a reinforced concrete (RC) bridge over the Koyoshi River, a class A river, was completed in 1979. Its eight bridge columns and seven spans give it maximum span length of 38.0 m.

We conducted measurements at the first span of the bridge as seen from JR Ugohonjyo Station. Measurements were restricted by sensor settings and other concerns. The span, shown by red circle in Figure 3 is 31.1 m long. It has a lower chord member of H-steel below the RC wheel guard. The cord member is then fastened to strong RC bridge columns by bolt joints. See the elevation view in Figure 3.

No damage or crack was found before our test by visual inspection of its exterior appearance, proper periodical maintenance was done on it. Inspections proved its structural integrity.

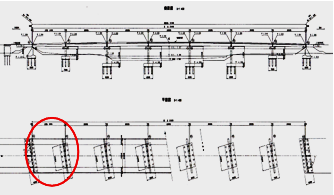Figure 3. Scheme of target structure for measurement. The target is a girder type bridge with seven spans

2.3. Sensor Laying Operation and Measurement Method

Detailed locations and laying configurations of sensors are portrayed in Figure 4(a). Five sets of accelerometer and piezoelectric sensors were fixed on the back side of floor slab like stethoscopes, making contact with human skin, marked as in the figure. In Figure 4 (b) and Figure 4 (c) sensors 1, 3, and 2, 4 along that direction. Furthermore, sensor 5 and the laser sensor were set in the upward direction at the central part of the slab floor, as shown in Figure 4 (f). The radio unit is shown as (e) of the same figure, setting of laser sensors as (f) with sensor settings for measuring the shear force using the conventional method as (h).We conducted measuring tests for moving and static truck loads using our simple measuring system of an accelerometer and laser displacement meter.

Figure 4. Presents some details of the sensor setup. Fundamentally, the relative displacements between the girders and support structure were measured at each point

Figure 5 depicts the fundamental configuration of our simple smart sensing system used in the test. Figure 5(a) demonstrates the configuration of our simple measuring system using piezoelectric sensor. All measuring operations were controlled by a PC through wireless transmission. Data from a single-board computer were sent to the PC through a Zigbee wireless module to be stored and analyzed there. A single-board computer admitting information from sensors and Zigbee transmitting data required a power supply.

Figure 5 (b) shows the conventional system configuration. A PC controlled our measuring system including the accelerometer (PV-87; Rion Co. Ltd.), sensors 1–7 wired to a preamplifier (VP-26A; Rion Co. Ltd.), a vibration meter (UV-05; Rion Co. Ltd.), and a recording-analysis device (EDX-2000A; Kyowa Electronic Instruments Co. Ltd.) and (CDV-40A; Kyowa Electronic Instruments Co. Ltd.). Fuji Technical Research Center assisted our measuring operations.

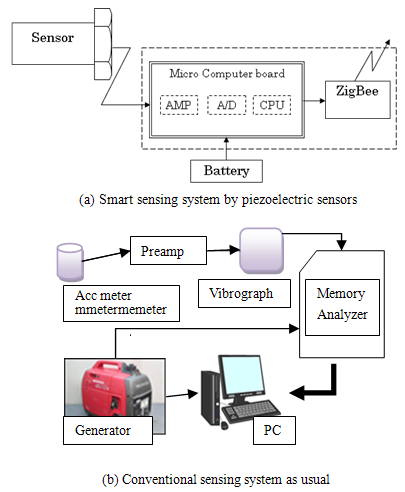Figure 5. The proposed monitoring sensors system

We inserted piezo-cable 80-mm-long into the center of hollow cylinder of urethane resin (φ15 mm × 80 mm) and fixed it using adhesive to produce a cylindrical sensor similar to a bolt as depicted in Figure 6 [18]. Jacketed lead wire of 4-mm-diameter and 1.5 m long was connected to the sensor and insulated. It was later wired to single-board computer. The sensor outputs voltage corresponding to cable deformation sent to processing devices of our system that measured displacement and vibration caused by cars and other vehicles passing over the bridge. This design concept underpins our simple measuring system portrayed in Figure 7.

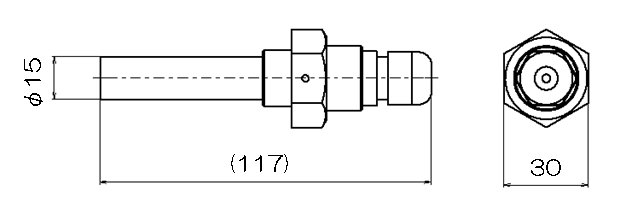Figure 6. Piezoelectric vibration sensor [17]

Figure 7. Piezoelectric vibration sensor for structural health monitoring system

Sets of piezoelectric sensors and accelerometers were fixed at measuring locations on the bridge side-by-side. A piezoelectric sensor of sensor 5 was set on a jig mounted on a steel member of the bridge: Figure 4(c). Furthermore, accelerometers were set to make contact with the floor slab. Their output was compared with that of piezoelectric sensor. Our simple piezoelectric sensor was mounted on a slab just making contact with it like a stethoscope touches human skin, as portrayed in Figure 4(h). This mounting, which was done for the convenience of sensor settings, was quite different from the former method of inserting a sensor into a fastener member of a flying bridge joint to measure the shearing force.

We conducted stationary-load and moving-load tests using a truck during PM 10:00 and AM 1:00, confirming that no cars were coming. Using this fixed load, we measured the vertical vibration and displacement of the floor slab at load passing speeds of 20, 40 and 60 km/h. Using the truck location and the instance of its of passing over sensors as a trigger signal, we made comparison tests between piezoelectric sensors and the accelerometer at sensors 1–4 and that between a piezoelectric sensor and the laser displacement meter at sensor 5. The sampling frequency was 100 Hz. Each measurement time was 2 min.

A video camera to monitor the truck and other vehicles was set upstream of the bridge and stored video pictures. In a temporary building constructed on the river bed, we collected, stored, and analyzed signals from piezoelectric sensors using a laptop computer (VAIO VGN-G3; Sony Corp.) through wireless transmission. The accelerometer outputs were wired to 5 channel amplifiers and the vibration analysis, storage, and display devices.

3. Comparison of Measured Vibration and Displacement

3.1. Fundamental Characteristics of Piezoelectric Sensors

Fundamental characteristics of piezoelectric sensors were verified preliminarily by room tests on vibration test devices related to frequency responses and relations between displacement and output. Configuration of the vibration test device is shown in Figure 8 (a) and frequency vs. output measured in Figure 8(b). Setting methods of sensors were changed from conventional insertion into a joint hole on the metal surface to measure the shearing force [18] to fixing a piezoelectric sensor on a jig as a stethoscope resting on human skin. We measured the output voltage of the piezoelectric sensor, changing the amplitude (both side) of the vibration test device 0.05 mm initially, then 0.1, and finally 0.2 mm progressively. The amplitude was measured by the laser displacement sensor set outside. According to the result we verified almost linear relation between frequency and output voltage for each amplitude, which convinced us to use the sensor for our tests. Finally we tested frequency response of the sensor to verify the sensor performance. It indicated stable measurement capability up to 40 Hz, Figure 8 (c).

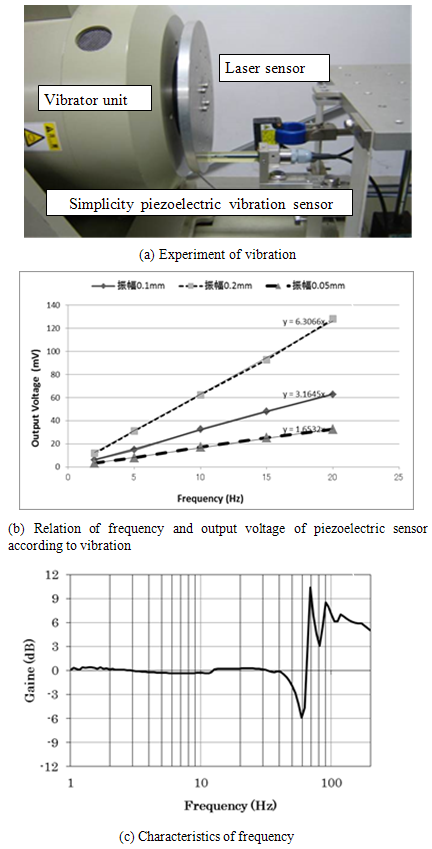Figure 8. Characteristic of sensors experiment

3.2. Measured Natural Frequency

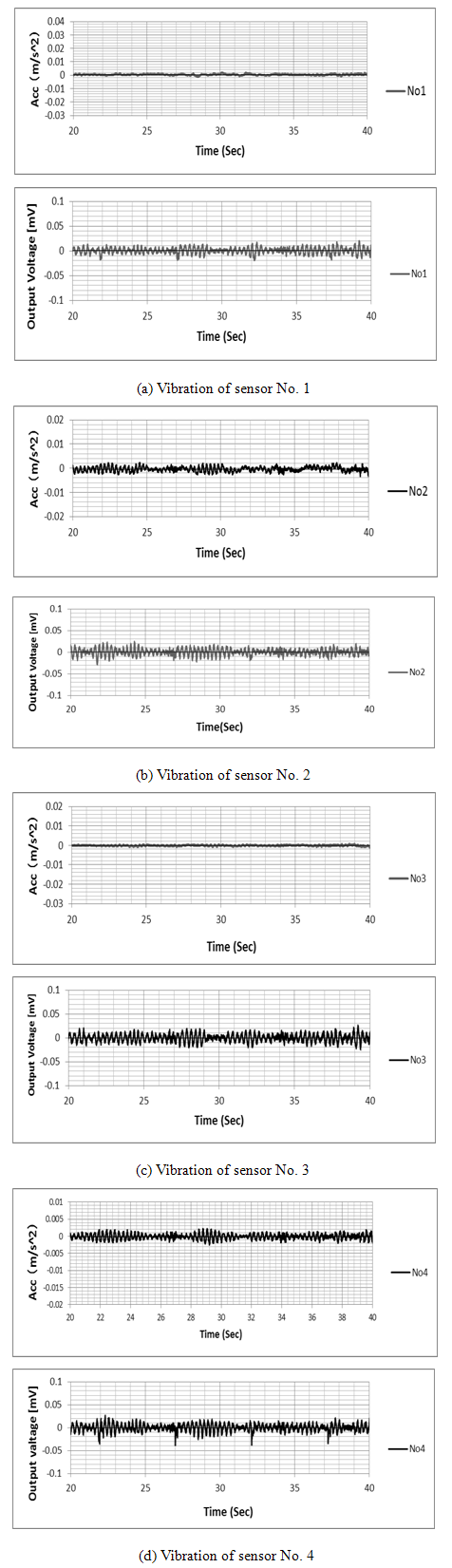
(1) Evaluation of the waveform and natural frequency

We conducted performance tests on the piezoelectric sensor and conventional accelerometer simultaneously to examine the performance of the former. After FFT analysis of the signals of these two sensors, we compared the natural frequencies that were found. Figure 9 demonstrates and compares the output signals of these sensors 1–4 for vertical free vibration before the truck approached at 20 km/h.

Figure 9. He upper part of Figure portrays acceleration responses obtained using accelerometers. The bottom part of the figure shows the voltage output from the bolt sensors. From recorded signals, predominant frequencies were obtained using Fourier analysis

Figure 10 portrays screen displays after FFT processing for signals of Figure 9. Comparison of the top display for the accelerometer and the bottom display for the piezoelectric vibration sensors output of voltage.

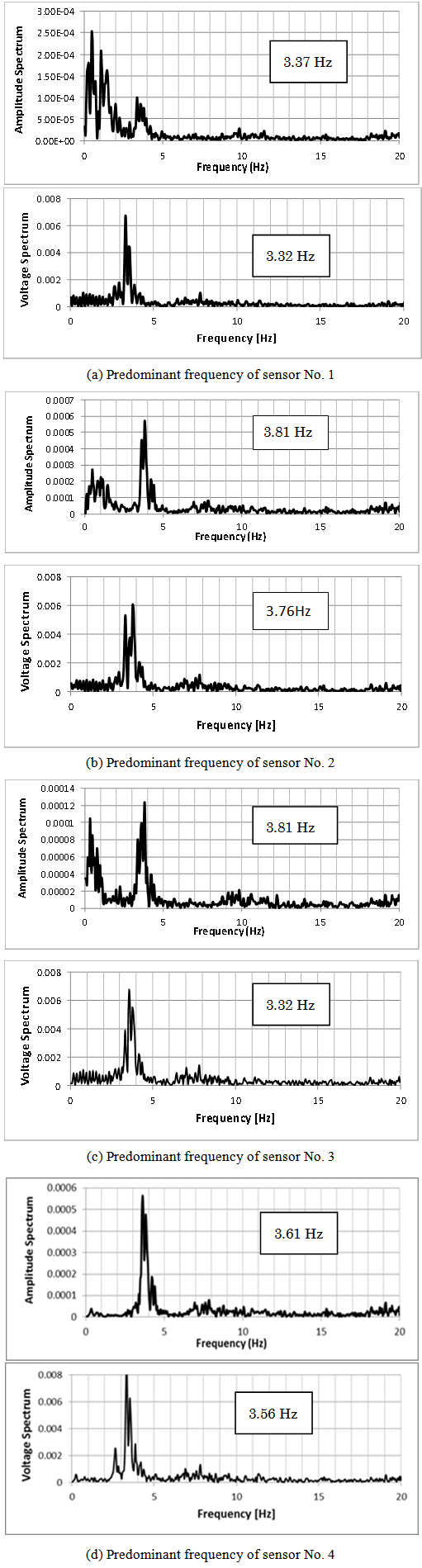Figure 10. Te Fourier spectrum for signals from points No. 1 to No. 4 are shown

We recorded sensors signals for continue two minutes to measuring. Compared signals for recording time of maximum natural frequency found by later for FFT analyzing and that for 20 s time zone before the truck passage on the sensors. Although we find no distinctive difference between the two waveforms of top and bottom displays in Figure 9, the two signals seem to be mutually synchronized. In natural frequencies presented in Fig. 10, although results for sensors 1–4 provide some similarity between two sensors, in general evaluation of accelerometers suggests the effectiveness of piezoelectric sensors.

(2) Evaluation of change of natural frequency with transit speed of a load truck over a sensor

We then assessed the change of natural frequency with the speed of a truck passing over the sensor making use of FFT of vertical vibration signal. The accelerometer gave the following results: 3.6–3.8 Hz for 20 km/h, 3.5–3.9 Hz for 40 km/h, and 3.3–3.8 Hz for 60 km/h. The piezoelectric sensor gave the following results: 2.6–3.8 Hz for 20 km/h, 2.6–3.1 Hz for 40 km/h, and 2.5–3.2 Hz for 60 km/h. Results show that the change of natural frequency with the passing speed of the load over the sensor was large at slower speeds such as 20 km/h, but seemed slightly higher at 40–60 km/h.

3.3. Mparison of Measured Data between Piezoelectric Sensor and Laser Displacement Sensor

We compared vertical deflections of the floor slab as measured by piezoelectric sensors and laser displacement sensors at sensor 5. Output from these two sensors is presented in Fig. 11. These were measured at sensor 5 portrayed in Fig. 4(a). Output from the piezoelectric sensor is drawn by solid line and that of laser displacement sensor by a broken line. In this test, the truck passed over these sensors at a speed of 20 km/h. Recovery from deflection after the truck left was well followed.

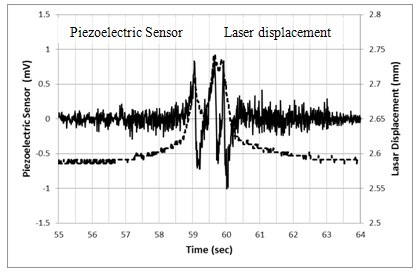Figure 11. Comparison of a proposed sensor response and the laser displacement transducer response

The laser displacement sensor recorded maximum deflection of some 0.15 mm. The piezoelectric vibration sensor recorded around 0.9 mm in this test. Correspondence between a bulging period of waveform and the trace of the truck position indicated good synchronization between truck movement and sensor detection. This confirmation and the good correlation between output of the laser displacement and output voltage of piezoelectric sensor, as demonstrated in the characteristics of Fig. 8(b), show the possibility of proposing an equation to estimate deflection using the piezoelectric sensor output and a simple relation. The natural frequency found by sensor 5 accelerometer at the same condition simultaneously was 3.55 Hz on average, and that by sensor 5 piezoelectric sensor was 3.2 Hz, on average.

3.4. Identifying the Natural Frequency by the Formula

(1) Fundamental principle

The dynamic nature of the bridge is a system of simple harmonic vibrations by its mass and structural stiffness. Equation (1) yields the natural frequency of a simple girder. Its deflection might be found by Equation (2) if it is uniformly loaded [19], [20]. Substituting that deflection into Equation (3), one might confirm the consistency of the natural frequency found by Equation (1).

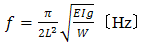(1)

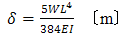(2)

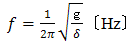(3)

where f denotes the natural frequency, g stands for the acceleration of gravity, δ represents the maximum deflection by dead load, W denotes the bridge weight per unit length, L signifies the beam length, E represents the modulus of longitudinal elasticity (Young modulus), and I is the second moment of the area.

Substituting L=3110 cm, EI=15.2×10¹² kg•cm²,ｇ=9.8×10² cm/s² and W= 40.8 kg/cm found from the bridge design into Equation (1), we obtained the natural frequency f of about 3.1 Hz. Then substituting W= 40.8 kg/cm, L=3110 cm, E=2.1×10⁶ kg/ cm², and I = .2×10⁶ cm⁴ into Equation (2), we found deflection δ of about 3.28 cm. Insertion of this deflection δ into Equation (3) provided the natural frequency of about 2.8 Hz. This result of obtaining natural frequency by Equation (3) close to that by Equation (1) underscores the reliability of measured values obtained by our piezoelectric sensor. The following are some supplementary descriptions. We found natural frequencies measured using the piezoelectric sensor and accelerometer fixed at sensor 5 in Fig. 4(a) for a truck running at 20 km/h when it passed over the pavement immediately above the sensor. The average of the natural frequency found through FFT processing of measurement by accelerometer was 3.57 Hz. That by piezoelectric sensor was 3.2 Hz. Therefore, results confirmed that we were able to obtain natural frequency by measurement using piezoelectric sensor that was comparable to that calculated using simple formulas. Summing up, the natural frequency for vertical vibration of the first span of Asuka Ohashi Bridge was 2.64–3.76 Hz by measurement through the piezoelectric sensor. That by measurement through the accelerometer was 3.37–3.81 Hz. That by simple formulas was 3.1–3.2 Hz, and that by FEM analysis was 3.4 Hz.

4. Conclusions

The following are the result of our tests related to natural frequency and deflection of Asuka Ohashi Bridge that were obtained through vibration analysis of measurements using a simple measuring system making use of a piezoelectric sensor and accelerometer.

FFT processing of measured data at sensors 1–4 on bridge floor slab yielded the natural frequency of 3.4–3.8 Hz for the accelerometer and that of 3.3–3.8 Hz for the piezoelectric sensor.

Close coincidence between two natural frequencies reported above might prove the effectiveness of our simple measuring system. Additional measurements using a precision vibration meter set on upper part of bridge done to confirm our measurement provided natural frequency of 3.61 Hz verifying the effectiveness of our system.

Simple formulas of structural mechanics using design data of bridge gave 3.1 Hz as the natural frequency and about 3.28 cm of maximum deflection for a dead load. Substituting this deflection into another simple formula yielded 2.8 Hz as a reference value and FEM analysis gave 3.36 Hz. On comparing these calculated natural frequencies to average value of 3.55 Hz found by FFT processing of measured data by accelerometer at sensor 7, one can conclude that this 3.55 Hz is close to the FEM value and value by the simple formula. This point confirms the reliability of our sensor system.

Because the natural frequency obtained using the simple formula and the one that we measured were close to the approximate natural frequency, we speculated that we were able to find the maximum deflection for dead load inserting the natural frequency obtained by our system into Equation (3) for the natural frequency.

Synchronization between outputs of laser displacement meter and piezoelectric sensor when they measured deflection of floor slab suggested an existing correlation between these two outputs. Accumulating data and establishing a simple formula directly from output of sensor, we might estimate the deflection at deformation by load.

Our system seems superior to the conventional one using an accelerometer: it does not need a power supply for the sensor during measuring operations, it has enhanced convenience because of its wireless transmission of data, and its cost is one-seventh of the conventional system cost.