1. Introduction

Gamma-ray linear attenuation coefficient describes the absorption of gamma-rays in unit length of an absorber material. This quantity depends on the energy of the incident gamma-ray beam and the density of the absorptive material.

Photon penetration in matter is governed statistically by the probability per unit distance travelled that a photon interacts by one physical process or another. This probability, denoted by µ, is called linear attenuation coefficient and has the dimensions of inverse length (e.g. cm^-1)[1]. When an incident gamma beam with the intensity of I₀ collide perpendicularly with an absorber with the thickness of x, the intensity (I) passing through the absorber can be evaluated with this equation:

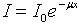(1)

Fig. 1 illustrates this equation.

NaI(Tl) (Sodium iodide activated with thallium) is one of the most commonly used inorganic scintillation detectors for gamma ray detection [2]. Inorganic crystals have great stopping power because their densities and atomic numbers are high. This feature is advantage of the inorganic crystals[3].

PSD is a kind of timing method that discriminate pulses produced by different types of incident particles to the detector surface. In this method, firstly the input signal (a) is attenuated by a significant fraction of the pulse amplitude (b). Then, the input signal is inverted and delayed (c). Finally, a bipolar timing signal is generated by adding signals which are in (b) and (c)[4]. This timing method is shown in Fig. 2.

Neutron-gamma separation[5, 6, 7, 8], background reduction and noise discrimination[9], improvement of energy resolution[10, 11] and pure particle identification[12, 13] are possible by this method.

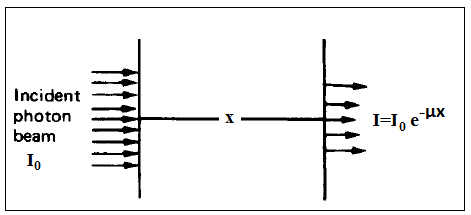Figure 1. Monoenergetic photons incident on a slab[4]

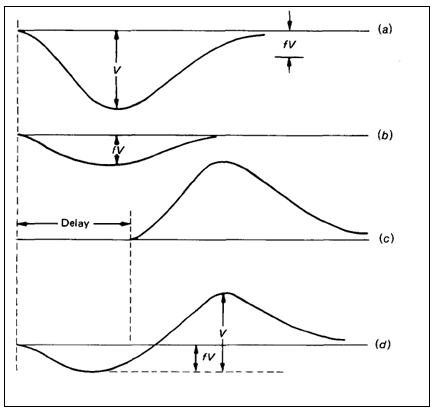Figure 2. The timing method [3]

This work suggests a different spectrometer for determining gamma-ray attenuation coefficients of materials by using PSD timing technique. The gamma-ray attenuation coefficients of Pb, plexiglass and bakelite materials were investigated through this technique and the obtained experimental coefficients were compared from the results of Xcom code.

2. Experiments

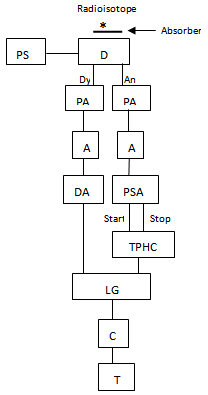
Fig. 3 illustrates the schematic diagram of the used spectrometer.

Figure 3. Used setup for determining the linear attenuation coefficient. (D: Detector and photomultiplier base, PS: Power Supply, PA: Preamplifier, A: Amplifier, PSA: Pulse Shape Analyzer, TPHC: Time to Pulse Height Converter, DA: Delay Amplifier, LG: Linear Gate, C: Counter, T: Timer)

Ortec model 401A BIN, Bicron 3x3 inch NaI(Tl) inorganic scintillation detector with Ortec model 266 photomultiplier base (PMB), Ortec model 456 power supply (Bias voltage: 1000 V), Ortec model 113 preamplifiers (Input capacity: 100 pF) , Ortec model 485 amplifiers (CG: 32, FG: 6), Ortec model 427A delay amplifier (Delay: 1.25 µs), Ortec model 426 linear gate, Ortec model 776 counter, Ortec model 719 timer, Ortec model 552 pulse shape analyzer and Ortec model 437A time to pulse height converter (Range: 200 ns) were used in the spectrometer. The NaI(Tl) detector has an aluminum window of 0.5 mm to protect it from the ambient light.

The spectrometer has consisted of two branches as could be shown in Fig. 3. In the first branch, fast timing signals from the photomultiplier base of the detector (An) were sent to PSA through the preamplifier and the main amplifier. PSA and TPHC are the main parts of the PSD technique and they are used for the time derivation. PSA produces two output signals dependent on the rise time in the interval of 10-90% of the input pulse. Its outputs were then sent to the TPHC to produce a time signal. The TPHC gives an output pulse whose amplitude is proportional to time difference between its start and stop input signals.

The rise time of the analog signal produced by the detector of the photopeak radiation is different from that of the rise time of the non-photopeak radiation, discriminating of the non-photopeak radiation signal from the photopeak signal. This is the main procedure of the PSD method.

In the second branch of the spectrometer, slow energy signals from the PMB of the detector (Dy) through preamplifier, main amplifier and delay amplifier were gated with the timing signals from the first branch in the linear gate device. Thus, only photopeak radiations from the radioisotope were chosen and used in the measurements.

Most common gamma radiation source ¹³⁷Cs (5 µCi) was used in the spectrometer. It was the disk shaped standard source with the diameter of 25 mm. The source was put about 4 cm away from the detector surface.

In order to test the setup, different types of absorbers as shielding materials were used. Pb, plexiglass and bakelite materials in plate shape, which plexiglass and bakelite have 10 cm x 10 cm dimensions with the thicknesses of 2 mm and Pb has same dimensions but 1 mm thickness, were chosen for determining the linear attenuation coefficients, and placed in front side of the detector. Data acquisition time was chosen as 60 s similar to the conventional attenuation setups[14, 15]. The counts from the detector were recorded versus different absorber thicknesses. These recorded counts were subtracted from the mean background value (925 counts/min.) and the semi-logarithmic absorption graphs of the absorbers were generated by using the background-free counts.

662 keV-energy photopeak position from the result of main amplifier output in energy spectrum and the TPHC output (time spectrum) were superimposed on same channel on the MCA in order to discriminate the non-photopeak radiations from the photopeak radiations.

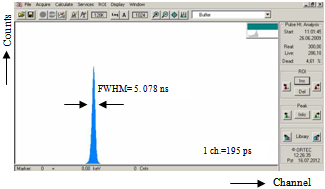Figure 4. The obtained time spectrum

3. Results and Discussions

The obtained time spectrum, which is the timing output of the TPHC, through the used timing method is shown in Fig. 4.

The time resolution value was found as 5.078 ns from this figure. Corresponding time per unit channel of MCA was calculated as 195 ps from this time spectrum by dividing the TPHC range to the conversion gain (1024 ch.) of the MCA.

Obtained energy spectrum (black) and the gated energy spectrum with timing signals (blue) are shown in Fig. 5. The energy resolution value was calculated as 4.22%.

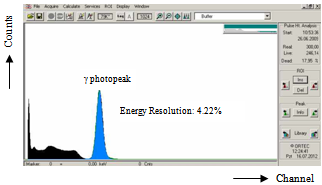Figure 5. Source spectrum (black) and the gated spectrum with timing signals (blue)

Gamma-ray attenuation graphs for the absorbers from the spectrometer were shown in Figs. 6 and 7, separately.

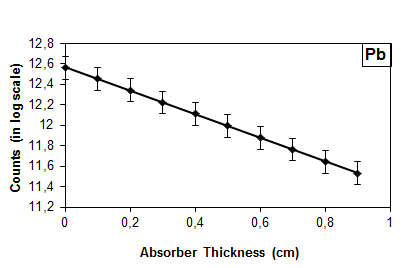Figure 6. Gamma-ray attenuation graph for Pb

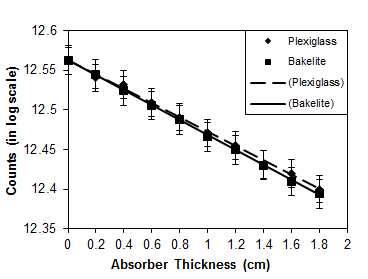Figure 7. Gamma-ray attenuation graphs for plexiglass and bakelite absorbers

The slope of the absorption graph gives the experimental gamma-ray linear attenuation coefficient of the absorber material in terms of cm^-1. In addition, the gamma-ray linear attenuation coefficients of the absorber materials were calculated from the mass attenuation coefficient results obtained from the Xcom code (version 3.1) developed by Berger and Hubbel[16].

In Fig. 7, the linear line was the absorption graph for bakelite and the dashed line corresponded to the absorption graph of plexiglass.

Theoretical coefficient values from the program and the experimental coefficient values for 662 keV-energy photopeak radiations of ¹³⁷Cs were given in Table 1.

Table 1. Theoretical and experimental gamma-ray linear attenuation coefficients for Pb (ρ=11.35 g.cm-3), plexiglass (ρ= 1.19 g.cm-3) and bakelite (ρ= 1.25 g.cm-3) absorber materials for 662 keV energy (ρ: density) Linear Attenuation Coefficients (cm-1) Pb Plexiglass Bakelite Theoretical 1.1747 0.0990 0.1018 Experimental 1.1497±0.0027 0.0891±0.0012 0.0948±0.0005

Rao and Gregg[17] have reported that the linear attenuation coefficient of plexiglass is 0.1006 cm^-1 for 662 keV energy. Goswami and Chaudhuri[18] have found 1.2167 cm^-1 value for Pb and compared this result with the other reference values for the same energy.

From the overall comparison of the coefficients, it can be accepted that all experimental coefficient results agree with the theoretical values from the Xcom code. Due to the fact that the reference coefficient values for bakelite could not be reached, no comparison between obtained results and reference results could be performed.

Furthermore, experimental coefficients for Pb and plexiglass accord with the reference results within the estimated errors.

Due to only photopeak radiations that used in the experiments, it was believed that the experimental coefficient values normally have been found smaller than that of Xcom and reference ones.

4. Conclusions

Gamma-ray linear attenuation coefficients of Pb, plexiglass and bakelite absorber materials were investigated by using PSD timing method for 662 keV energy.

Coefficient values for the absorber materials used in the setup are agreed well with the ones obtained from the Xcom program and the reference values.

In addition to gamma attenuation coefficients via timing method, beta attenuation coefficients were obtained in Ref.[19] by using the method. It is concluded from these results that the timing technique can be used for determining both the gamma and beta-ray linear and mass attenuation coefficients of materials.

It has been shown in this work that the spectrometers for determination of gamma-ray absorption coefficients using PSD timing method might be an alternative for the conventional gamma absorption setups.

ACKNOWLEDGEMENTS

This work was supported by TUBITAK, the Scientific and Technological Research Council of TURKEY under project number 197T087 and by EBILTEM, Center of Science and Technology, Ege University under Project No. 99 BIL 001.