1. Introduction

The equipment replacement problems involve items that degenerate with the usage or with the passage of time and those that fail after a certain amount of use or time. Those items that deteriorate with time are likely to be old and/or costly, e.g., machine tools, automotives, ships, heavy equipment and home appliances.

The replacement study can be classified into two main categories [1]:

1. Replacement of assets that deteriorate with time, which mean replacement due to gradual failure, or wear and tear of the components of the machines. This can be further classified into the following types: Determination of economic life of an asset, and replacement of an existing asset with a new asset.

2. Simple probabilistic model for assets that fail completely which means replacement due to sudden failure.

The economic life of an equipment means to determine the period during which it remains financially viable for its owner. This needs to consider the operating costs, maintenance, and potential revenue. Equipment replacement can be considered as a long-term investment. The equipment economic lifespan can vary from an equipment to the other.

This depends mainly up on various factors and parameters such as the technology, market conditions, and regulations. Figure (1) shows the equipment costs versus levels of maintenance activity, while the dash line illustrates the minimum cost which determines the best time to replace the equipment.

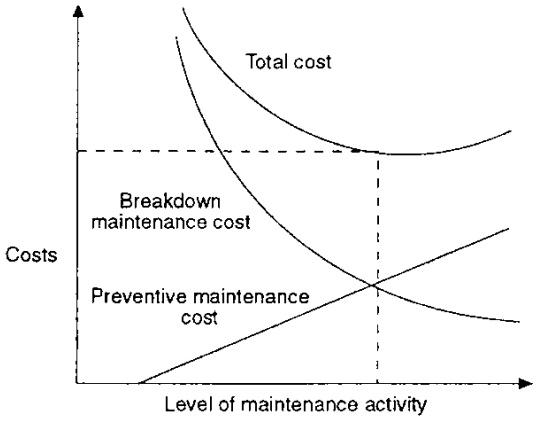Figure (1). Equipment Economic Life [1]

The equipment replacement refers to the process of replacing old or inefficient machinery or equipment with a more efficient models. This decision is crucial in maintaining operational efficiency, reducing maintenance costs, and minimizing downtime. Factors such as equipment age, repair costs, and advancements in technology influence the timing of replacement. Business owners need to evaluate whether the cost of repairs outweighs the benefits of keeping outdated equipment. Proper equipment replacement planning ensures improved productivity, safety, and energy efficiency. Additionally, modern equipment often complies with newer environmental regulations, further justifying the investment in replacements for long-term business sustainability.

Through the equipment life-period, it generates income but at the same time it is incurring operating costs. Over time, maintenance costs rise as the equipment ages, and mechanical components become less efficient. At a certain time, the equipment needs to be replaced to stop loses. The equipment replacement strategies can be applied to any equipment, vehicle, planes, railroads, heavy equipment or ships. As an example, Govert et al [2] use a unique dataset containing information on the timing of accidents, inspections, ship particular changes of more than fifty thousand ships over a 29-year time-period. The results of their duration analysis reveal that the shipping industry is a relative safe industry but there is a possible over-inspection of vessels.

Once a piece of equipment is purchased and used, it eventually begins to wear out and suffers mechanical problems. At some point, it reaches the end of its useful life and must be replaced. Thus, a major element of profitable equipment fleet management is the process of making the equipment replacement decision [3]. The equipment economic life is a balance of operating costs, technological advancements, regulatory requirements, and market conditions. Owners must continuously evaluate these factors to decide when to retire or replace their equipment. There are huge parameters affecting the economic life of the equipment [4]. Heuristic and dynamic programming models of equipment replacement are included in [5].

In this paper, a comparative study between heuristic and sophisticated mathematical programming equipment replacement models is presented with emphasis on multi-objective optimization with fuzzy parameters. These decision-making techniques consider trade-offs in various objectives, including minimizing costs and maximizing operational efficiency under uncertainty. The subsequent sections summarize the various methods and highlight each of their respective pros and cons.

2. Models to Determine the Equipment Economic Life

Heuristic Models

Heuristic models can be used to tackle the equipment replacement problem. Such models can serve as a source for decision-making simple rules in practice instead of complex optimization methods. Heuristic models are usually derived from experience, intuition or rules of thumb and come in hand when exact mathematical models are either non-existent or prohibitively expensive to compute. These models seek to contain not the optimal solution, but a relatively efficient one in a reasonable amount of time. Some authors give this an extreme attention, and they spent a good efforts to prepare their heuristic models for equipment replacement.

3. Common Heuristic Models for Equipment Replacement

1. Age-Based Heuristic:

Rule: No Matter How Good It Is Still Working, Replace the Gear If it has Reached a Specific Age.

Rationale: Equipment is subject to failure and thus degradation over time, these heuristic models take the decision-making ease by pre-defining best age of replacement (e.g. replace every 10 years).

Example: instead of keeping track of the individual mileage, a company replaced its fleet of vehicles once every 7 years.

Pros and Cons: Straightforward implementation and keeps equipment up-to-date regularly but could force earlier replacement of serviceable systems, which is more expensive. These models are introduced in [5], [6] and [7].

2. Usage-Based Heuristic:

Rule: Replace equipment based on a set number of hours, cycles, or miles after use as opposed to focusing in its true age.

Rationale: Equipment many times gets worn out as it is used with high intensity or on regular basis. Usage offers a better indication of when to replace it than age does.

Example: an airline might change its jet engines after a certain number of flight hours. This is done regardless of the age of the engines in calendar days.

Pros and Cons: Closer to real world usage, giving you more accurate replacement timing. These models also necessitate tracking the usage in quite some detail, which could be expensive or challenging to ascertain for some industries. Metrics are introduced in [8], [9], and [10].

3. Failure-Based Heuristic:

Rule: Replace after a set number of failures or once the failure rate reaches an acceptable level, this is the rule.

Rationale: This method emphasizes dependability using equipment until it starts to be overly unreliable, or when he upkeep costs spike.

Example: A factory could say that it replaces a machine after it has failed three times in the same year. They believe that it is no longer trustworthy.

Pros and Cons: Guarantees equipment is updated before it becomes expensive or inconvenient to run. These are not proactive, but reactive models. If equipment background after failure, these models can use to decree through higher downtime and inefficiencies. This is in reference to [11], [12], and [13].

4. Maintenance Cost-Based Heuristic:

Rule: Replace when maintenance exceeds a percentage of replacement cost.

Rationale: This comparisons compares the cost to continuously pay for repair or maintenance against the price of new equipment. It means that you must discontinue use when the upkeep is no longer economical.

Example: A company may choose to replace a machine when the cost of maintaining the machine in one year is greater than 20% oof the value of acquiring new machine.

Pros and Cons: It weighs the cost of maintenance against the cost of equipment replacement to offer a clear threshold on when financial action is warranted. They depend on the ability to track maintenance costs precisely and have reliable replacement cost info. Such models are listed in [10], [14], [15], and [16].

5. Economic Life Heuristic:

Rule: Replace equipment to minimize the annualized total cost (capital + operating + maintenance costs).

Rationale: It estimates the optimal economic life of equipment considering the trade-off between purchase costs and increased maintenance costs as time passes.

Example: A firm finds that changing out machinery every 8 years results in the lowest total annual cost of ownership.

Pros and Cons: Provides a balance between capital and operating expenses, maximizing cost-efficiency. These models require detailed cost data and analysis to determine the optimal replacement point. Such models are introduced by [9], [11], [17], and [18].

6. Salvage Value Heuristic:

Rule: Replace equipment when its market value (salvage value) falls below a predefined level, or when it is no longer makes financial sense to operate the equipment.

Rationale: Equipment that has a high resale value might be replaced earlier to capture that value, especially when depreciation outpaces operational costs.

Example: A company may sell a truck after 5 years, while its resale value is still high. They do this to avoid a steeper decline in its value over the next few years.

Pros and Cons: This maximizes the return on the equipment’s residual value. But salvage value fluctuations can make timing difficult. Replacing equipment solely based on resale value may overlook operational efficiency. These models are introduced by [9], [17], [19], and [20].

7. Opportunity Cost Heuristic:

Rule: Replace equipment when the opportunity cost of keeping the current equipment exceeds the benefit of investing in new technology or equipment.

Rationale: This approach factors in the potential lost benefits from using outdated equipment when more efficient or advanced options become available.

Example: A factory may replace older machinery that operates at 80% efficiency with newer models that offer 95% efficiency to save energy and boost productivity.

Pros and Cons: Accounts for technological advancements and the potential for higher productivity with newer equipment. They requires careful analysis of future technology and its potential impact on operations. Such models are included in [5], [6], and [21].

8. Replacement Interval Heuristic:

Rule: Replace equipment at fixed intervals, regardless of age, usage, or condition.

Rationale: This simplifies to make the decision by setting regular intervals to replace the equipment (e.g., every 5 years). They do this based on historical data or company policy.

Example: A fleet of buses might be replaced every 6 years based on historical data. Showing that buses tend to deteriorate significantly after that period.

Pros and Cons: Simple and easy to implement, predictable costs But they are inflexible. Could trigger the swapping of still-functional equipment or increase utilization of obsolete tech respectively. Some of these heuristic models are proposed in [5], [6], [21] and [22].

9. Cost-Per-Unit Output Heuristic:

Rule: Replace equipment if the price per unit of output (for example, if the price per product, for example, cost per service) exceeds a certain limit.

Rationale: This method assesses the cost effectiveness of equipment against the output it provides and indicates when replacement is more economical than working with highly inefficient models.

Example: An operating unit such as a printing press may be replaced when the cost of producing each printed page at that operating unit exceeds a determined threshold due to increasing maintenance costs and efficiency decay.

Pros and Cons: Centred on cost-effectiveness as well as productivity. They do, however, depend on precise monitoring of both costs and production — something that might be impossible in some sectors. Those models are presented in [5], [6] and [22].

4. Benefits of Heuristic Models for Equipment Replacement Problem

Simplicity: Heuristics offer straightforward, easy to apply rules for making decisions.

Speed: These models enable fast decisions without the need for extensive mathematical optimization.

Practicality: Heuristic models are derived from real experience and industry best practices making them more intuitive to managers and operators.

5. Drawbacks of Heuristic Models for Replacement Problem

Sub-optimal Solutions: A heuristic model does not ensure to provide the optimal solution. Making it likely to cost more — in the long term.

Oversimplification: Heuristic models can forget factors by narrowing to only one or two (like age or usage) Like, for example technological innovations or variations in market situations.

Lack of Flexibility: Set rules may not work with changing business environments or specific equipment conditions.

6. Mathematical Programming Models

Operations Research (OR) began during the second World War. This done when scientists were tasked with optimizing military operations. British and American teams of mathematicians, engineers, and scientists worked to improve the efficiency of logistics, radar deployment, and resource allocation. Their success in enhancing military operations through analytical methods led to the formalization of OR as a discipline. After the war, the Operations Research expanded to industries such as manufacturing, transportation, and healthcare. This is to help organizations to make data-driven decisions. Year after year, the field has evolved, incorporating new mathematical models, algorithms, and computer technologies to solve complex, large-scale optimization problems. The operations research includes many branches. A group of them is the mathematical programming. In addition to the mathematical programming, there are more other topics like network analysis, game theory, inventory control, reliability and maintenance, etc... There are huge books and published papers which illustrates operations research and its branchesas in [23], [24], [25], [26], [27] and more other books and papers.

Mathematical Programming include Linear Programming (LP), Non-linear Programming (NLP), Integer Programming (IP), Dynamic Programming (DP), Goal Programming, and Stochastic Programming. The replacement problem was modelled and solved by many authors using the different branches of mathematical programming as follows:

7. Linear Programming

Linear programming (LP) is a mathematical method branch, which is used to find the best possible outcome in each situation, subject to some certain constraints. It involves optimizing a linear objective function, which represents the obectives such as maximizing profit or minimizing cost, while considering a set of linear inequalities or equalities as constraints like resource limitations. Linear programming problems typically involve decision variables that need to be determined. The solution helps to find the optimal values of these variables. This method is widely used in various applications such as economics, business, engineering, and logistics for planning and decision-making. The equipment replacement is formulated by linear programming as in [28], [29], [30], and [31].

8. Integer Programming

Integer programming (IP) is a type of mathematical optimization. Some or all the decision variables are required to be integers. This method is used when the solution to a problem must consist of discrete values rather than continuous ones, like in non-integer or linear programming.

There are different types of integer programming:

1. Pure Integer Programming: All variables are restricted to integer values.

2. Mixed Integer Programming (MIP): Some variables are restricted to integers. But others can be non-integer.

3. Binary Integer Programming: The variables can only take on values of 0 or 1 (used for "yes/no" decisions).

Integer programming is used in many practical applications where only whole numbers make sense, such as in scheduling, resource allocation, production planning, and network design.

Integer programming is applied by many authors to formulate and solve the equipment replacement problem as in [32], [33], [34], [35], and [36].

9. Goal Programming

Goal programming is an extension of linear programming. It used to handle problems with multiple, often conflicting objectives. Instead of optimizing a single objective function, goal programming allows for the simultaneous achievement of several goals. Each one of which may have different priorities or importance. In goal programming, we need to:

Ø Define the goals. Each objective is expressed as a goal with a target value you aim to reach.

Ø Set priorities. Goals can be weighted or prioritized based on their relative importance.

Ø Minimize deviations. The goal is to minimize the deviation from these target values rather than optimizing a single objective.

This approach is particularly useful in decision-making problems where several objectives such as minimizing costs, maximizing customer satisfaction, and achieving production targets need to be considered together. The goal programming is applied to solve the replacement problem as in [37], [38], and [39].

10. Dynamic Programming

Dynamic programming (DP) is one of the mathematical optimization techniques. It is used to solve complex problems. D.P. solve problems by breaking them down into simpler sub-problems. It is particularly effective for problems that can be divided into overlapping sub-problems. The solutions to these smaller problems can be reused to solve the larger problems efficiently.

The key idea behind dynamic programming is to solve each sub-problem only once and store the result, typically in a table. This avoids redundant calculations and significantly reduces the time complexity compared to solving the same sub-problems multiple times [40].

Dynamic programming is often used in problems that involve decision-making over time, such as:

Shortest Path Problem, Knapsack Problem, Fibonacci Sequence calculation, Resource Allocation, Inventory Control problems, and Equipment Replacement Problem. There are two main approaches to dynamic programming:

Ø Forward D.P.: Solve the larger problem by recursively breaking it down. Start from sub-problem (1) and go forward to the last sub-problem (M). store the results of subproblems to avoid re-computation.

Ø Backward D.P.: Start by solving the smallest subproblems and iteratively build up solutions for larger subproblems. Start from the last sub-problem (M) then go backward to sub-problem (1).

The equipment replacement is formulated and solved by dynamic programming as in [41], [42], [43], [44], [45], [46] and [47].

11. Solution Algorithm of Equipment Replacement by Dynamic Programming

When solving the equipment replacement problem by backward dynamic programming we need to follow the following solution algorithm:

1. Arrange the problem data as shown in Table (1).

2. Divide the problem into sub-problems. If the company needs to prepare the replacement strategy for M-years, so, each year should represent a sub-problem. Let us call each sub-problem as a stage. So, we have M-stages.

3. The replacement decisions are: Keep and Replace. Keep: means to keep the equipment for a complete year and perform any required maintenance or repair. Replace: means to sell the equipment and buy another new one.

4. The replacement decision should be taken at the beginning of each stage.

5. At each stage define the problem state as follows:

Ø At stage (1): The state is the current equipment age. For example, if the equipment is 3-years old, then state (1) is 3.

Ø At stage (2): The state is 1 and 4. Why? If the decision at stage (1) was “Keep”, then at the beginning of stage (2), the equipment will be 4-years old. But if the decision was “Replace”, then at the beginning of stage (2), the equipment will be just 1-year old.

Ø State (3): 1, 2, and 5.

Ø State (4): 1, 2, 3, and 6.

Ø State (5): 1, 2, 3, 4, and 7.

6. The recursive equation of the backward dynamic programming to maximize the total profit is [41]:

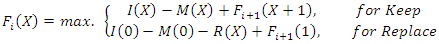Where:

Fi(X): return value at stage (i) for equipment of age (X).

I(X): total income at age (X).

M(X): total operating cost at age (X).

R(X): total replacement cost at age (X).

7. Prepare the solution stages as in Tables (2). Calculate the return value under both “Keep” and “Replace” decision at the different states (X). Compare these return functions at each state (X) to choose the maximum value and its related decision.

8. Get the optimal replacement strategy which represents one decision at stage, starting from stage (1) to stage (M).

9. The maximum profit for the studied plan is the total profit at stage (1).

12. Illustrative Example

Let us assume a company has a 3-years old machine and want to determine the optimal replacement strategy for this equipment for the next 5 years. The equipment data which include total income, total operating cost and total replacement cost at any age (X) of the equipment are summarized the Table (1).

Table (1). Income, operating cost, and replacement cost at different ages

This problem can be solved by backward dynamic programming in 5-stages as in Tables (2) below:

Tables (2). Solution stages for the equipment replacement problem

From the solution stages at Table (2), we can determine the optimal replacement policy as follows:

The maximum profit for this 5-years plan is $42970.

13. Conclusions

The equipment replacement problem can be solved by many methods and models. Some of them are heuristics which are great to find the best replacement policy and sometimes near optimal policy. Other authors used the mathematical programming models like, linear programming, integer programming, goal programming, dynamic programming, and more other related models. While the heuristic models are great to be used but the mathematical programming models gives the optimal replacement policy. More other advanced studies such as sensitivity analysis, parametric study, fuzzy parameters, and multi-objective studies can be applied to the mathematical programming models. These advanced models are important to know what will happen to the optimal solution if one or more parameters of the input data change with the time. The multi-objective is very important as well to get the best compromise solution when more than one conflict objectives are considered. This for sure illustrates how powerful are the mathematical programming models when studying the equipment replacement problem. Solution algorithm as well as an illustrative example are added to this paper to show how powerful and easy to apply dynamic programming to determine the optimal equipment replacement policy.