-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Traffic and Transportation Engineering
p-ISSN: 2325-0062 e-ISSN: 2325-0070
2020; 9(2): 37-40
doi:10.5923/j.ijtte.20200902.02

An Optimal Solution for a Real Transportation Problem with Lingo Code
Hilal A. Abdelwali, Mohsen Alardhi, Ahmad E. Murad, Jasem M.S. Al-Rajhi
Automotive and Marine Department, College of Technological Studies, PAAET, Kuwait
Correspondence to: Mohsen Alardhi, Automotive and Marine Department, College of Technological Studies, PAAET, Kuwait.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

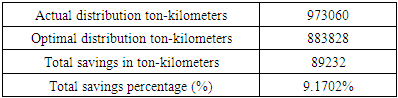
The transportation problem deals with finding the minimum cost of transporting a single product from a certain number of sources to a given number of destinations. The problem can be expressed by the formulation of a linear model, and it can be solved using the simplex algorithm. But due to its particular structure of the linear model, it can be solved with more efficient methods. LINGO is one of the compelling tools which can be used to solve optimization problems. It includes integrated packages that include powerful language for expressing related optimization models, a full-featured environment for both building and editing problems, and a set of fast built-in solvers. In this paper, a lingo code is prepared based on the formulation of transportation problems to solve an actual case study. The optimal solution of the studied case study reduces the total ton-kilometers by 9.1702 % of the real distribution amounts. The real data, the lingo code, the optimal solution, and a comparison between the real and optimal solutions are both included.
Keywords: Transportation problem, an actual case study, LINGO
Cite this paper: Hilal A. Abdelwali, Mohsen Alardhi, Ahmad E. Murad, Jasem M.S. Al-Rajhi, An Optimal Solution for a Real Transportation Problem with Lingo Code, International Journal of Traffic and Transportation Engineering, Vol. 9 No. 2, 2020, pp. 37-40. doi: 10.5923/j.ijtte.20200902.02.
1. Introduction
- Transportation problem is one of the most useful and applied branches of linear programming. It deals with finding the optimal distribution of goods from several sources to several destinations. The optimal distribution means that this distribution costs the lowest transportation cost, and there is no other distribution than the optimal one that costs less. Transportation problems can be solved to minimize transportation cost, distance, time, deterioration of goods, vehicle fuel consumption, etc... The transportation problem can also be solved to maximize the companies’ earnings, profits, etc.The transportation problem was first formalized by the French mathematician Gaspard Monge (1871) [1]. Tolstoi, A.N. was one of the first to study the transportation problem mathematically in the 1920s. In 1930, on the collection Transportation Planning Volume number 1, for the National Commissariat of Transportation for the Soviet Union, he published a paper Methods of Finding the Minimal Kilometers in Cargo-transportation in space. Tolstoi (1939) illuminated his approach by applications to the transportation of salt, cement, and other cargo between sources and destinations along the railway network of the Soviet Union. In particular, for that large-scale, instance of the transportation problem was solved to optimality. F.L. Hitchcock (1941) worked on the distribution of products from several sources to numerous localities. Koopman also worked on the optimum utilization of the transportation system and used a model of transportation, in activity analysis of production and allocation. It is known as the Hitchcock Koopman transportation problem [2].Usually, the solution to the transportation problem passes through three main steps. These steps include finding the initial basic feasible solution, the test of optimality, and moving towards optimality. Enormous researches were prepared to find the initial basic feasible solution as well as the other two steps [3-5]. But different ways give the optimal solution directly. Out of these methods are the Lingo codes and excel solver.More advanced researches were carried out to solve the fuzzy transportation problem, multi-objective transportation problem, multiple criteria transportation problem, multi-index, multi-level transportation problem, and transshipment [2,6-12].In this paper, we prepared a lingo code to solve the transportation problem while applying this code to solve a real-world problem with actual data. The prepared lingo code based on the transportation problem technique is used to solve a real transportation problem. The actual problem deals with re-distributing flour, which is produced in middle Egypt milestones to warehouses. The company milestones exist in 16 different cities. The flour was required to be distributed to 5 governorate cities, which are 26 major cities.
2. Transportation Problem
- The main parts of the transportation problem are the number of sources “m”, the number of destinations “n” and the unit costs “cij” of transporting goods from each source “i=1,2,…,m” to each destination “j=1,2,…,n”. The amounts of goods that should be transported from source “i” to destination “j” is xij. The total transportation cost “Z” can be calculated using the following transportation model:
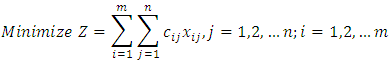 Subject To:
Subject To: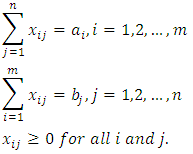 By solving the above model of the transportation problem, we’ll get the optimal solution to the problem. This model is used to build a lingo code to solve an actual transportation problem, as in the following sections.
By solving the above model of the transportation problem, we’ll get the optimal solution to the problem. This model is used to build a lingo code to solve an actual transportation problem, as in the following sections.3. Lingo
- LINGO is a well-known and powerful Operational Research software tool available today designed to make building and solving problems easier and more efficient. It is designed to build and solve Linear, Nonlinear, Quadratic, Quadratically Constrained, Semi-Definite, Second Order Cone, Integer and Stochastic optimization models faster, easier, and more efficient. LINGO includes integrated packages that include a powerful language for the aim of expressing optimization models, a full-featured environment for editing and building problems, and a set of fast built-in solvers.Lingo lets us formulate our linear, nonlinear and integer problems quickly in a highly readable format. LINGO modeling language allows us to express models in a straight-forward intuitive manner using summations and subscripted variables, much like we would with pencil and paper. The key benefits of LINGO are easy model expression, convenient data options, create turn-key applications and extensive documentation and help [13].Models become more comfortable to build, easier to understand, and, therefore, much easier to maintain. LINGO can also exploit multiple CPU cores for faster model generation. Lingo codes were prepared to solve transportation problem examples as in [14-16].
4. Case Study
- M.E.M.C. is a big company that produces and distributes flour in 5 governorates in Egypt. Their mills exist in 16 cities while the company distributes flour to 26 major cities. The company produces several types of flour. The collected data of this problem include the distances in kilometers between all cities where mills exist, to all cities where they want to send flour. Also, all mills availabilities and all major cities requirements in tons through the studied month. Table (1) represents the collected data.
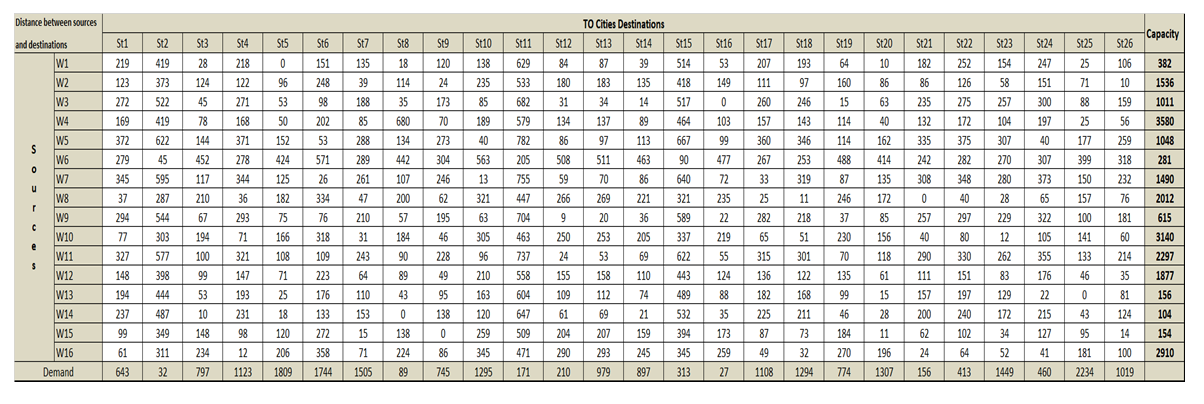 | Table 1. Transportation problem collected data sources capacity and destination demands and distances between them |
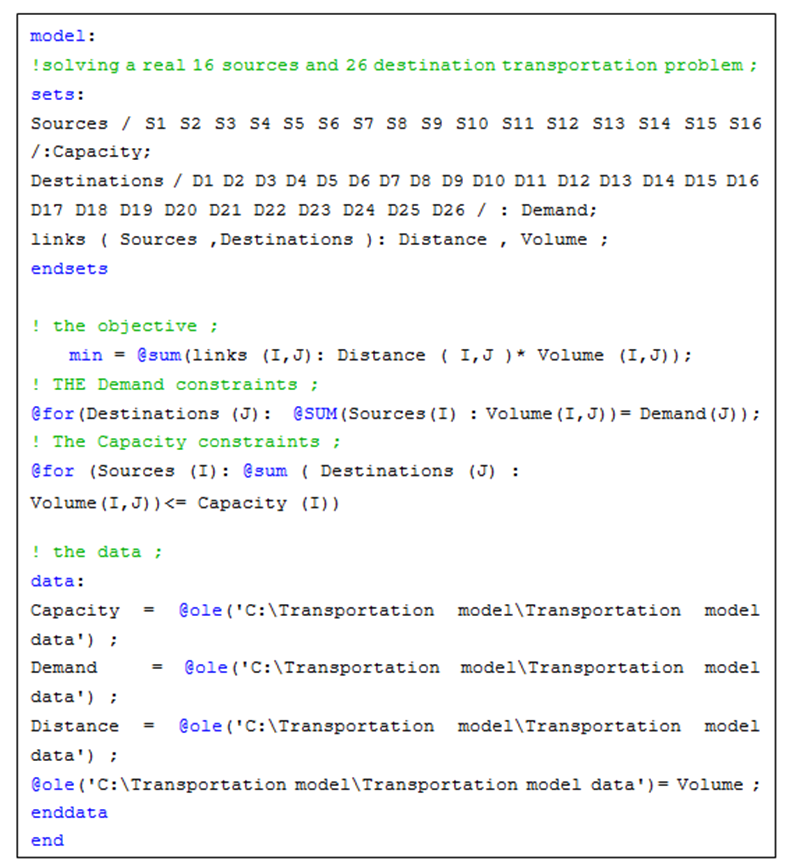 | Figure 1. Lingo code for the studied transportation problem |
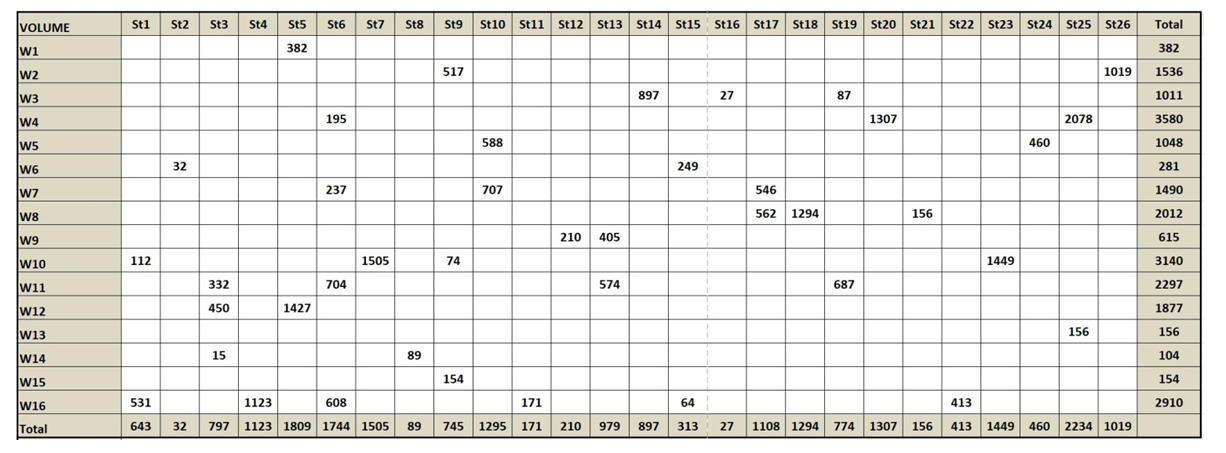 | Table 2. Transportation problem actual distribution between sources and destination in (ton) |
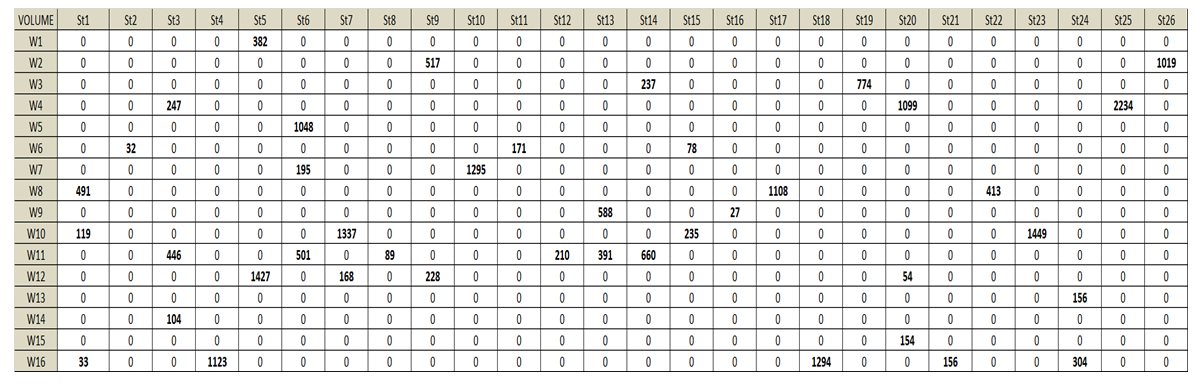 | Table 3. The optimal distribution of M.E.M.C. flour from sources to each destination |
|
5. Conclusions
- A LINGO code is prepared and applied to solve an actual transportation problem. Lingo is a potent, fast, and easy tool to solve such transportation problems. The case study is a mills company called M.E.M.C. that exists in middle Egypt. We could achieve the optimal distribution of flour from the company mills which exist in 16 cities to 26 major cities. The total ton-kilometers of the actual distribution was 973,060. Total ton-kilometers of the optimal distribution is 883,828. The generated optimal solution could reduce a total of 89,232 ton-kilometers, which represents 9.1702 % of the actual ton-kilometers. Both lingo code, actual and optimal distribution of flour are included in this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML