| [1] | D. Dardari, E. Falletti, and M. Luise, Satellite and terrestrial radio positioning techniques: a signal processing perspective. Academic Press, 2011. |
| [2] | W. H. L. Neven, T.J. Quilter, R. Weedon, and R. A. Hogendoorn, “Wide area multilateration,” NLR, Report on EATMP TRS 131, 04, 2005. |
| [3] | Q. Liu, S. Han, and X. S. Ma, "Research of time delay estimation based on higher order statistics," In Applied Mechanics and Materials, vol. 33, no. 9, pp. 550–553, 2014. |
| [4] | C. Knapp and G. Carter, "The generalized correlation method for estimation of time delay," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 24, no. 4, pp. 320–327, 1976. |
| [5] | H. Dou, Q. Lei, W. Li, Q. Xing, “ A new TDOA estimation method in Three-satellite interference localisation,” International Journal of Electronics, vol. 102 no. 4, pp. 839-54, 2015. |
| [6] | D. Oh, S. Kim, S.-H. Yoon, and J.-W. Chong, "Two-Dimensional eSPRIT-like shift-invariant TOA estimation algorithm using multi-band Chirp signals robust to carrier frequency offset," IEEE Transactions on Wireless Communications, vol. 12, no. 7, pp. 3130–3139, 2013. |
| [7] | P. Marmaroli, X. Falourd, and H. Lissek, "A Comparative Study of Time Delay Estimation Techniques for Road Vehicle Tracking," in Proceedings of the 11th French Congress of Acoustics and 2012 Annual IOA Meeting, Acoustics 2012. |
| [8] | G. Galati, M. Leonardi, P. Magaro, and V. Paciucci, "Wide area surveillance using SSR mode S Multilateration: Advantages and limitations," European Radar Conference, 2005. EURAD 2005., pp. 225–229, 2005. |
| [9] | X. Li and K. Pahlavan, "Super-resolution TOA estimation with diversity for indoor Geolocation," IEEE Transactions on Wireless Communications, vol. 3, no. 1, pp. 224–234, Jan. 2004. |
| [10] | Y. Li, S. Go, H. Yoo, S. Kim, and J.-W. Chong, "TOA estimation algorithm based on shift-invariant technique for multi-band signals," in AETA 2013: Recent Advances in Electrical Engineering and Related Sciences. Springer Science + Business Media, 2014, pp. 241–246. |
| [11] | K. Haneda, K. i. Takizawa, J. i. Takada, M. Dashti and P. Vainikainen, "Performance evaluation of threshold-based UWB ranging methods - Leading edge vs. search back -," 2009 3rd European Conference on Antennas and Propagation, Berlin, 2009, pp. 3673-3677. |
| [12] | C. Steffes, R. Kaune, S. Rau, and F. Fkie, "Determining Times of Arrival of Transponder Signals in a Sensor Network using GPS Time Synchronization," in Jahrestagung der Gesellschaft für Informatik, Berlin, 2011. [Online]. Available: http://www.user.tu-berlin.de/komm/CD/paper/100123.pdf. Accessed: Nov. 10, 2016. |
| [13] | D. Oh, Y. Li, S. Liu, S.-H. Yoon, and J.-W. Chong, "Dual shift invariant TOA estimation algorithm for multi-band signals," IEEE Communications Letters, vol. 16, no. 10, pp. 1568–1571, Oct. 2012. |
| [14] | I. A. Mantilla-Gaviria, G. Galati, M. Leonardi, and J. V. Balbastre-Tejedor, "Time-difference-of-arrival regularised location estimator for multilateration systems," IET Radar, Sonar & Navigation, vol. 8, no. 5, pp. 479–489, 2014. |
| [15] | I. A. Mantilla-Gaviria, M. Leonardi, G. Galati, and J. V. Balbastre-Tejedor, "Localization algorithms for multilateration (MLAT) systems in airport surface surveillance," Signal, Image and Video Processing, vol. 9, no. 7, pp. 1549–1558, 2014. |
| [16] | X. Qu and L. Xie, "An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements," Signal Processing, vol. 119, pp. 142–152, 2016. |
| [17] | W. FOY, "Position-location solutions by Taylor-Series estimation," IEEE Transactions on Aerospace and Electronic Systems, vol. AES-12, no. 2, pp. 187–194, 1976. |
| [18] | I. A. Mantilla-Gaviria, M. Leonardi, J. V. Balbastre-Tejedor, and E. de los Reyes, "On the application of singular value decomposition and Tikhonov regularization to ill-posed problems in hyperbolic passive location," Mathematical and Computer Modelling, vol. 57, no. 7-8, pp. 1999–2008, 2013. |
| [19] | D. E. Chaitanya, M. N. V. S. S. Kumar, G. S. Rao, and R. Goswami, "Convergence issues of taylor series method in determining unknown target location using hyperbolic multilateration," 2014 International Conference on Science Engineering and Management Research (ICSEMR), 2014. |
| [20] | A. Z. Sha’ameri, Y. A. Shehu, and W. Asuti, "Performance analysis of a minimum configuration multilateration system for airborne emitter position estimation," Defence S and T Technical Bulletin, vol. 8, no. 1, pp. 27–41, Jan. 2015. |
| [21] | K. C. Ho, "Bias reduction for an explicit solution of source localization using TDOA," IEEE Transactions on Signal Processing, vol. 60, no. 5, pp. 2101–2114, May 2012. |
| [22] | Y. Weng, W. Xiao, and L. Xie, "Total least squares method for robust source localization in sensor networks using TDOA measurements," International Journal of Distributed Sensor Networks, vol. 2011, pp. 1–8, 2011. |
| [23] | L. Yang and K. C. Ho, "An approximately efficient TDOA localization algorithm in closed-form for locating multiple Disjoint sources with erroneous sensor positions," IEEE Transactions on Signal Processing, vol. 57, no. 12, pp. 4598–4615, Dec. 2009. |
| [24] | Y. T. Chan, K. C. Ho, “A simple and efficient estimator for hyperbolic location,” IEEE Trans. Signal Proces, vol 42, 8, pp.1905-1915, 1994. |
| [25] | M. D. Gillette and H. F. Silverman, "A linear closed-form algorithm for source localization from time-differences of arrival," IEEE Signal Processing Letters, vol. 15, pp. 1–4, 2008. |
| [26] | R. Fujiwara, K. Mizugaka, T. Nakagawa, D. Maeda, and M. Miyazaki, "TOA/TDOA hybrid relative positioning system based on UWB-IR technology," IEICE Transactions on Communications, vol. E94-B, no. 4, pp. 1016–1024, 2011. |
| [27] | Y. Jiang, H. Qing, and D. Kai Yang, "Hybrid TOA-TDOA Positioning Algorithm in AIS," Advanced Material Research, vol. 655, pp. 876–881, 2013. |
| [28] | L. Cui-Xia, L. Wei-Ming, and F. Zi-Nan, "GPS/TDOA hybrid location algorithm based on federal Kalman filter," Journal of Convergence Information Technology, vol. 5, no. 7, pp. 42–48, 2010. |
| [29] | X. Zhang and Z. Ning, "Hybrid tdoa and toa based positioning system," U.S. Patent Application 13/236,259, filed 2011. |
| [30] | M. R. Gholami, S. Gezici, and E. G. Strom, "Improved position estimation using hybrid TW-TOA and TDOA in cooperative networks," IEEE Transactions on Signal Processing, vol. 60, no. 7, pp. 3770–3785, 2012. |
| [31] | J. Yi, Q. Hu, and D. Yang, "A novel position estimation method using hybrid TOA and TDOA in AIS," Journal of Convergence Information Technology, vol. 8, no. 5, pp. 1237–1245, 2013. |
| [32] | A. Doicu, T. R. Trautmann, and F. Schreier, Numerical regularization for atmospheric inverse problems. Heidelberg: Springer-Verlag Berlin and Heidelberg GmbH & Co. K, 2010. |



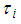 be the TOA measurement estimated at the i-th antenna station with coordinates
be the TOA measurement estimated at the i-th antenna station with coordinates 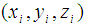 . The equation for the TOA measurement of the signal at the i-th antenna station transmitted from an emitter located at
. The equation for the TOA measurement of the signal at the i-th antenna station transmitted from an emitter located at 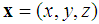 is
is 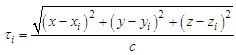
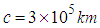 From eq. 1, there is a nonlinear relationship between the aircraft location (x) and the TOA measurement
From eq. 1, there is a nonlinear relationship between the aircraft location (x) and the TOA measurement 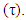 Taking the square of both sides in eq. 1 will results to
Taking the square of both sides in eq. 1 will results to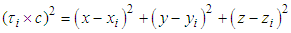
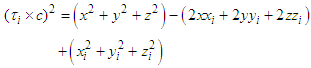
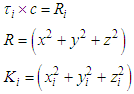
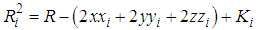
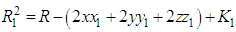
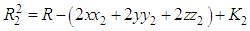
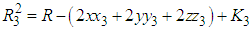
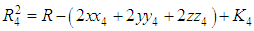
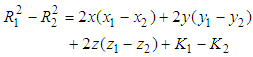
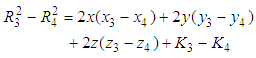
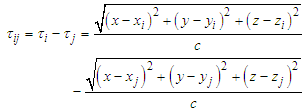
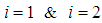 as reference pair for obtaining the TDOAs, 4 number TDOA hyperbolic equations are obtained as
as reference pair for obtaining the TDOAs, 4 number TDOA hyperbolic equations are obtained as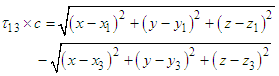
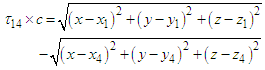
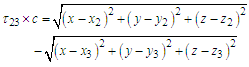
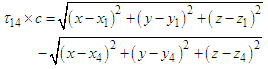
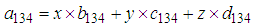
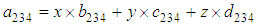
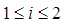 and
and 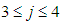 are
are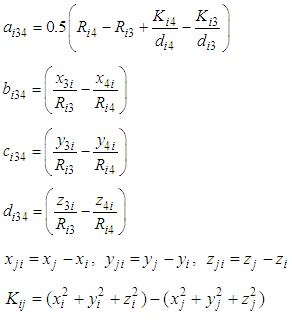
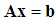
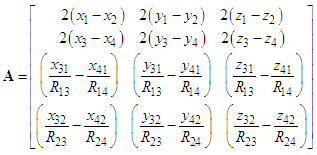
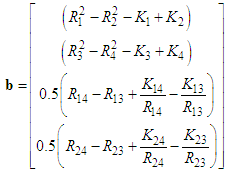
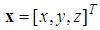
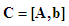
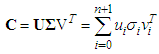
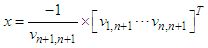

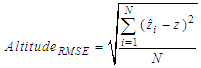
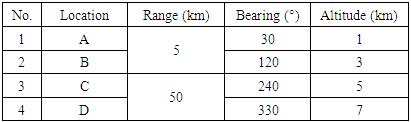
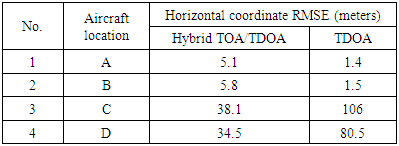
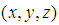 correspond to the known aircraft location and
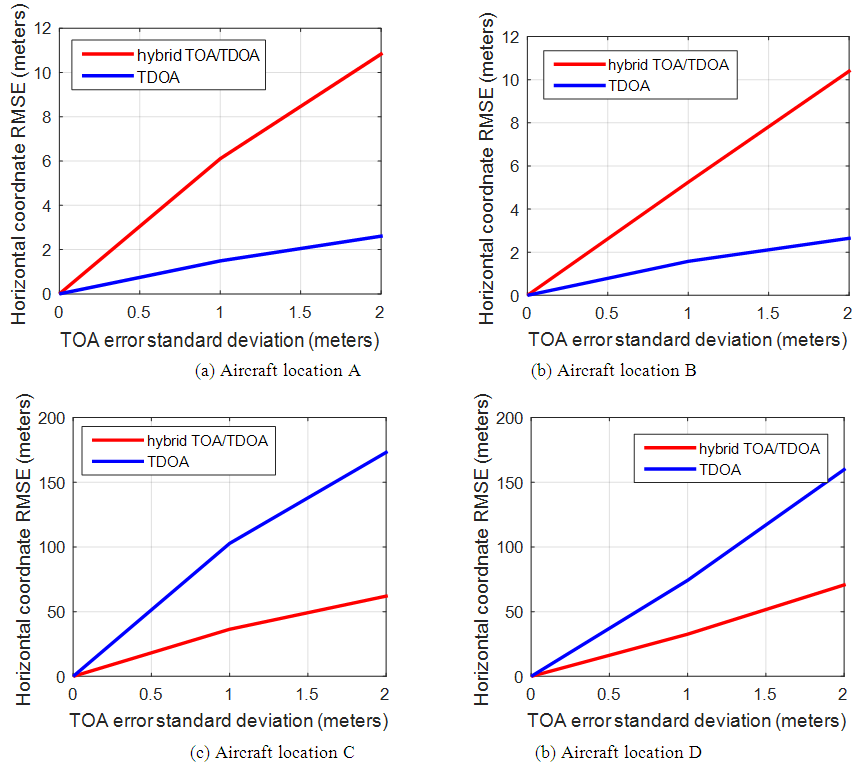
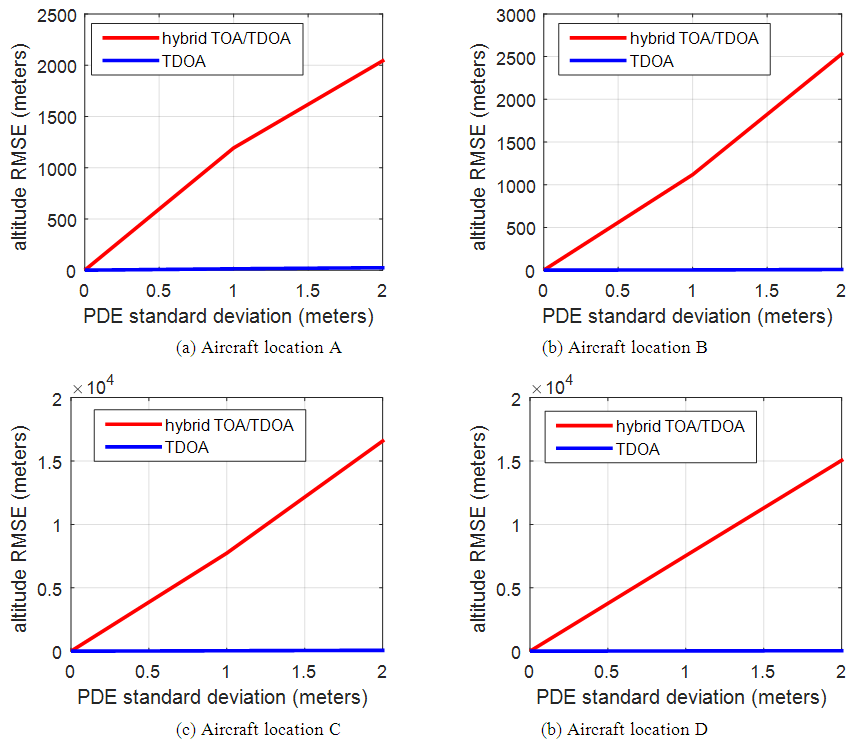
correspond to the known aircraft location and 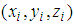 is the estimated aircraft location at the i-th Monte Carlo simulation iteration. Monte Carlo simulation results are obtained after 500 iterations. The error in the TOA measurement error is assumed as to have a Gaussian distribution with zero mean and σ standard deviation. The estimated TOA measurement in distance at the i-th GRS is
is the estimated aircraft location at the i-th Monte Carlo simulation iteration. Monte Carlo simulation results are obtained after 500 iterations. The error in the TOA measurement error is assumed as to have a Gaussian distribution with zero mean and σ standard deviation. The estimated TOA measurement in distance at the i-th GRS is 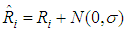
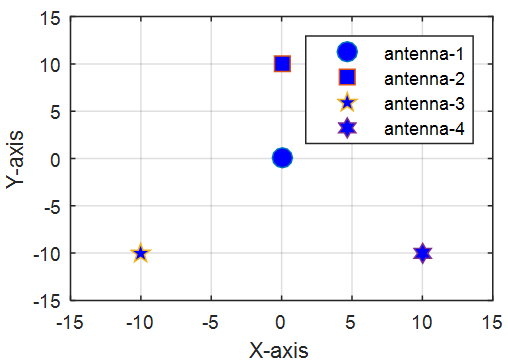
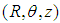 . Conversion from cylindrical coordinate system to the Cartesian coordinate system
. Conversion from cylindrical coordinate system to the Cartesian coordinate system 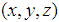 can be done using the equations below.
can be done using the equations below. 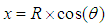
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML