| [1] | P. C. M. Leung and E. W. M. Lee, “Estimation of electrical power consumption in subway station design by intelligent approach,” Applied Energy, vol. 101, pp. 634–643, January 2013. |
| [2] | C. Winston and V. Maheshri, “On the social desirability of urban rail transit systems,” Journal of Urban Economics, vol. 62, no. 2, pp. 362–382, September 2007. |
| [3] | X. Feng, H. Zhang, Y. Ding, Z. Liu, H. Peng, and B. Xu, “A review study on traction energy saving of rail transport” Discrete Dynamics in Nature and Society Volume 2013 (2013), Article ID 156548, 9 pages [Online] Available: http://dx.doi.org/10.1155/2013/156548. |
| [4] | A. R. Miller, J. Peters, B. E. Smith, and O. A. Velev, “Analysis of fuel cell hybrid locomotives,” Journal of Power Sources, vol. 157, no. 2, pp. 855–861, July 2006. |
| [5] | Railway technical web pages. Railway systems, technologies and operations across the world [Online]. (Available:www.railway-technical.com). |
| [6] | C. S. Chang and S. S. Sim, “Optimising train movements through coast control using genetic algorithms,” IEE Proceedings—Electric Power Application, vol. 144, no. 1, pp. 65–73, January 1997. |
| [7] | K. K. Wong and T. K. Ho, “Coast control for mass rapid transit railways with searching methods,” IEE Proceedings: Electric Power Applications, vol. 151, no. 3, pp. 365–375, May 2004. |
| [8] | H. Hwang, “Control strategy for optimal compromise between trip time and energy consumption in a high-speed railway,” IEEE Transactions on Systems, Man, and Cybernetics A, vol. 28, no. 6, pp. 791–802, November 1998. |
| [9] | M. S. Yang, “A survey of fuzzy clustering,” Mathematical and Computer Modelling, vol. 18, no. 11, pp. 1–16, September 1993. |
| [10] | R. Liu and I. M. Golovitcher, “Energy-efficient operation of rail vehicles,” Transportation Research A, vol. 37, no. 10, pp. 917–932, Desember 2003. |
| [11] | Y. V. Bocharnikov, A. M. Tobias, C. Roberts, S. Hillmansen, and C. J. Goodman, “Optimal driving strategy for traction energy saving on DC suburban railways,” IET Electric Power Applications, vol. 1, no. 5, pp. 675–682, September 2007. |
| [12] | K. Kim and S. I. Chien, “Simulation-based analysis of train controls under various track alignments,” Journal of Transportation Engineering, vol. 136, no. 11, pp. 937–948, November 2010. |
| [13] | D. Bertsimas and J. Tsitsiklis, “Simulated annealing,” Statistical Science, vol. 8, no. 1, pp. 10–15, 1993. |
| [14] | K. Kim and S. I. Chien, “Optimal train operation for minimum energy consumption considering track alignment, speed limit, and schedule adherence,” Journal of Transportation Engineering, vol. 137, no. 9, pp. 665–674, September 2011. |
| [15] | H. Liu, B. Mao, Y. Ding, W. Jia, and S. Lai, “Train energy-saving scheme with evaluation in urban mass transit systems,” Journal of Transportation Systems Engineering and Information Technology, vol. 7, no. 5, pp. 68–73, October 2007. |
| [16] | H. H. Hoang, M. P. Polis, and A. Haurie, “Reducing energy consumption through trajectory optimization for a metro network,” IEEE Transactions on Automatic Control, vol. 20, no. 5, pp. 590–595, October 1975. |
| [17] | D. N. Kim and P. M. Schonfeld, “Benefits of dipped vertical alignments for rail transit routes,” Journal of Transportation Engineering, vol. 123, no. 1, pp. 20–27, January 1997. |
| [18] | B. R. Ke, M. C. Chen, and C. L. Lin, “Block-layout design using maxmin ant system for saving energy on mass rapid transit systems,” IEEE Transactions on Intelligent Transportation Systems, vol. 10, no. 2, pp. 226–235, April 2009. |
| [19] | B. R. Ke, C. L. Lin, and C. W. Lai, “Optimization of train-speed trajectory and control for mass rapid transit systems,” Control Engineering Practice, vol. 19, no. 7, pp. 675–687, July 2011. |
| [20] | IFEU (Institutfür Energieund Umweltforschung Heidelberg GmbH), Energy Savings by Light-Weighting (Final Report), International Aluminium Institute (IAI), Heidelberg, Germany, 2003. |
| [21] | M. Chou and X. Xia, “Optimal cruise control of heavy-haul trains equipped with electronically controlled pneumatic brake systems,” Control Engineering Practice, vol. 15, no. 5, pp. 511–519, May 2007. |
| [22] | S. Lu, S. Hillmansen, and C. Roberts, “A power-management strategy for multiple-unit railroad vehicles,” IEEE Transactions on Vehicular Technology, vol. 60, no. 2, pp. 406–420, February 2011. |
| [23] | P. Lukaszewicz, Energy consumption and running time for trains: modelling of running resistance and driver behavior based on full scale testing [Ph.D. thesis], Royal Institute of Technology, Stockholm, Sweden, 2001. |
| [24] | X. Feng, “Optimization of target speeds of high-speed railway trains for traction energy saving and transport efficiency improvement,” Energy Policy, vol. 39, no. 12, pp. 7658–7665, December 2011. |
| [25] | X. Feng, B. Mao, X. Feng, and J. Feng, “Study on the maximum operation speeds of metro trains for energy saving as well as transport efficiency improvement,” Energy, vol. 36, no. 11, pp. 6577–6582, October 2011. |
| [26] | X. Feng, J. Feng, K. Wu, H. Liu, and Q. Sun, “Evaluating target speeds of passenger trains in China for energy saving in the effect of different formation scales and traction capacities,” International Journal of Electrical Power and Energy Systems, vol. 42, no. 1, pp. 621–626, November 2012. |
| [27] | D. Kraay, P. T. Harker, and B. Chen, “Optimal pacing of trains in freight railroads: model formulation and solution,” Operations Research, vol. 39, no. 1, pp. 82–99, February 1991. |
| [28] | A. Higgins, E. Kozan, and L. Ferreira, “Optimal scheduling of trains on a single line track,” Transportation Research B, vol. 30, no. 2, pp. 147–161, April 1996. |
| [29] | K. Ghoseiri, F. Szidarovszky, and M. J. Asgharpour, “A multi-objective train scheduling model and solution,” Transportation Research B, vol. 38, no. 10, pp. 927–952, December 2004. M. Brio, G. M. Webb, and A. |
| [30] | K. K. Wong and T. K. Ho, “Dwell-time and run-time control for DC mass rapid transit railways,” IET Electric Power Applications, vol. 1, no. 6, pp. 956–966, November 2007. |
| [31] | B. Sansò and P. Girard, “Train scheduling desynchronization and power peak optimization in a subway system,” in Proceedings of the IEEE/ASME Joint Railroad Conference, pp. 75–78, Baltimore, Md, USA, April 1995. |
| [32] | K. K. Wong and T. K. Ho, “Dynamic coast control of train movement with genetic algorithm,” International Journal of Systems Science, vol. 35, no. 13-14, pp. 835–846, August 2004. |
| [33] | T. Albrecht, “The influence of anticipating train driving on the dispatching process in railway conflict situations,” Networks and Spatial Economics, vol. 9, no. 1, pp. 85–101, November 2008. |
| [34] | F. Corman, A. D'Ariano, D. Pacciarelli, and M. Pranzo, “Evaluation of green wave policy in real-time railway traffic management,” Transportation Research C, vol. 17, no. 6, pp. 607–616, December 2009. |
| [35] | Y. Bai, T. O. Ho, and B. Mao, “Train control to reduce delays upon service disturbances at railway junctions,” Journal of Transportation Systems Engineering and Information Technology, vol. 11, no. 5, pp. 114–122, October 2011. |
| [36] | Y. Fu, Z. Gao, and K. Li, “Optimization method of energy saving train operation for railway network,” Journal of Transportation Systems Engineering and Information Technology, vol. 9, no. 4, pp. 90–96, August 2009. |
| [37] | M. C. Falvo, R. Lamedica, R. Bartoni, and G. Maranzano, “Energy management in metro-transit systems: an innovative proposal toward an integrated and sustainable urban mobility system including plug-in electric vehicles,” Electric Power Systems Research, vol. 81, no. 12, pp. 2127–2138, December 2011. |
| [38] | M. Coto, P. Arboleya, and C. Gonzalez-Moran, “Optimization approach to unified AC/DC power flow applied to traction systems with catenary voltage constraints,” International Journal of Electrical Power and Energy Systems, vol. 53, no. 1, pp. 434–441, December 2013. |
| [39] | T. Suzuki, “DC power-supply system with inverting substations for traction systems using regenerative brakes,” IEE Proceedings B, vol. 129, no. 1, pp. 18–26, January 1982. |
| [40] | M. B. Richardson, “Flywheel energy storage system for traction applications,” in Proceedings of the International Conference on Power Electronics, Machines and Drives, Conference Publication no. 487, pp. 275–279, Bath, UK, April 2002. |
| [41] | Y. Ding, F. Zhou, Y. Bai, and H. Liu, “Simulation algorithm for energy-efficient train following operation under automatic-block system,” Journal of System Simulation, vol. 21, no. 15, pp. 4593–4597, August 2009. |
| [42] | Y. Ding, B. Mao, H. Liu, T. Wang, and X. Zhang, “Algorithm for energy-efficient train operation simulation with fixed running time,” Journal of System Simulation, vol. 16, no. 10, pp. 2241–2244, October 2004. |
| [43] | S. Acikbas and M. T. Soylemez, “Coasting point optimisation for mass rail transit lines using artificial neural networks and genetic algorithms,” IET Electric Power Applications, vol. 2, no. 3, pp. 172–182, May 2008. |
| [44] | D. Anderson and G. McNeill, Artificial Neural Networks Technology: A DACS State-of-the-Art Report, Kaman Sciences Corporation, New York, NY, USA, 1992. |
| [45] | L. Yang, K. Li, Z. Gao, and X. Li, “Optimizing trains movement on a railway network,” Omega, vol. 40, no. 5, pp. 619–633, October 2012. |
| [46] | Y. Ding, H. Liu, Y. Bai, and F. Zhou, “A two-level optimization model and algorithm for energy-efficient urban train operation,” Journal of Transportation Systems Engineering and Information Technology, vol. 11, no. 1, pp. 96–101, February 2011. |
| [47] | A. P. Cucala, A. Fernández, C. Sicre, and M. Domínguez, “Fuzzy optimal schedule of high speed train operation to minimize energy consumption with uncertain delays and driver's behavioral response,” Engineering Applications of Artificial Intelligence, vol. 25, no. 8, pp. 1548–1557, December 2012. |
| [48] | W. Wang, X. Jiang, S. Xia, and Q. Cao, “Incident tree model and incident tree analysis method for quantified risk assessment: an in-depth accident study in traffic operation,” Safety Science, vol. 48, no. 10, pp. 1248–1262, December 2010. |
| [49] | K. Kim, “Optimal train control on various track alignment considering speed and schedule adherence constraints”, PhD thesis, New Jersey Institute of Technology, New Jersey, USA, 2010. |
| [50] | V. R. Vuchic, Urban Public transportation. Systems and Technology. New Jersey: Englewood Cliffs, 1981. |
| [51] | V. R. Vuchic, Urban Transit. Systems and Technology. New Jersey: John Wiley & Sons, 2007. |
| [52] | W.W. Hay, Railroad Engineering, 2nd ed., John Wiley& Sons, Inc., New York, N.Y., 1982. |
| [53] | S. Yeh, “Integrated analysis of vertical alignments and speed profiles for rail transit routes” MSc thesis, University of Maryland, Maryland, USA, 2003. |
| [54] | American Railway Engineering and Maintenance-of-Way association (AREMA). Economics of Railway Engineering and Operation, Train Performance, Manual for Railway Engineering, p.16-2-4, 1999. |
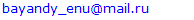
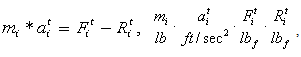
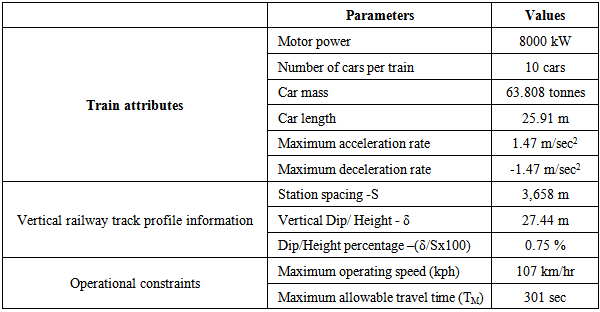
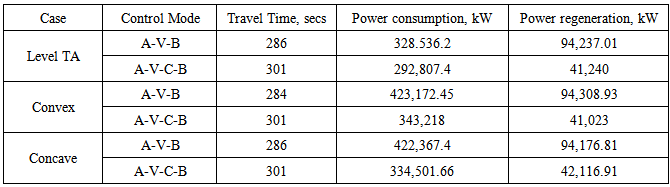
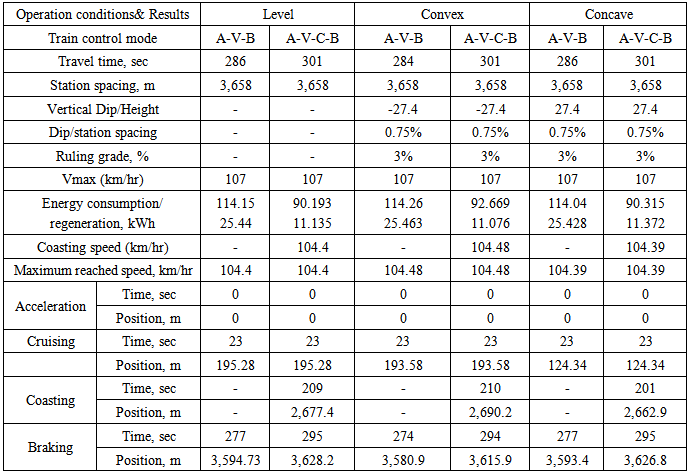
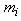 is car mass,
is car mass, 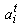 is acceleration of the ith car at time t,
is acceleration of the ith car at time t, 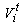 is speed of the ith car at time t,. However, in this model it was decided to proceed without the spring and damping coefficients due to the complexity of model and the limited time for the current project.In order to avoid slippery wheels on the track, the maximum TF at time t for the ith car, denoted as Ftmax(i), is the minimised amount of the propulsive Ftp(i) and adhesive Ftа(i) forces, respectively [2, 3-5].
is speed of the ith car at time t,. However, in this model it was decided to proceed without the spring and damping coefficients due to the complexity of model and the limited time for the current project.In order to avoid slippery wheels on the track, the maximum TF at time t for the ith car, denoted as Ftmax(i), is the minimised amount of the propulsive Ftp(i) and adhesive Ftа(i) forces, respectively [2, 3-5]. 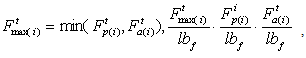
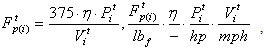
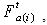 which is influenced by the mass of car Wi. The value of the adhesive coefficient μit depends on train speed. In the train performance simulation μit is found by the following equation [7].
which is influenced by the mass of car Wi. The value of the adhesive coefficient μit depends on train speed. In the train performance simulation μit is found by the following equation [7].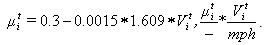
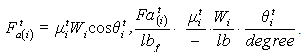
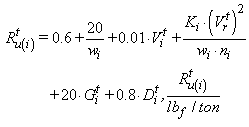
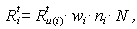
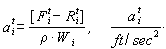
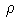 - Coefficient of rotating masses, (accepted as 1.04).The actual braking force Ftb(i) for the deceleration of a train can be calculated and has to be maximum value of the comfort-limited braking force Fbc or the adhesive–limited braking force Fba.
- Coefficient of rotating masses, (accepted as 1.04).The actual braking force Ftb(i) for the deceleration of a train can be calculated and has to be maximum value of the comfort-limited braking force Fbc or the adhesive–limited braking force Fba. 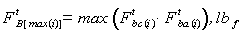
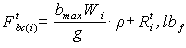
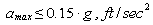
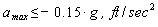
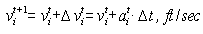
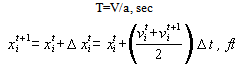
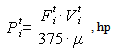
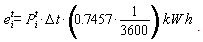
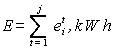
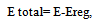
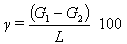
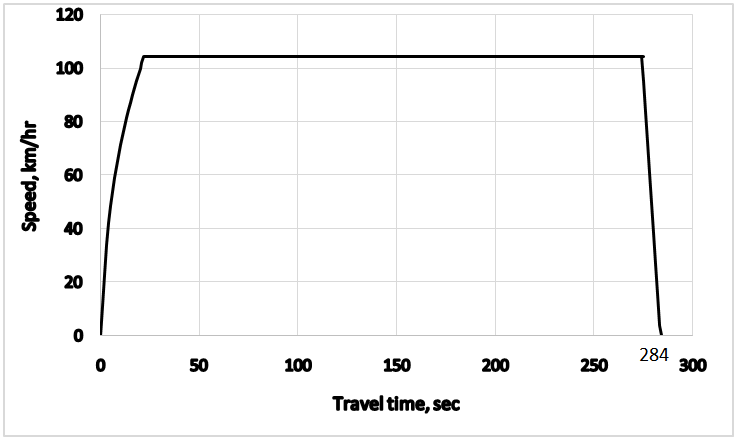
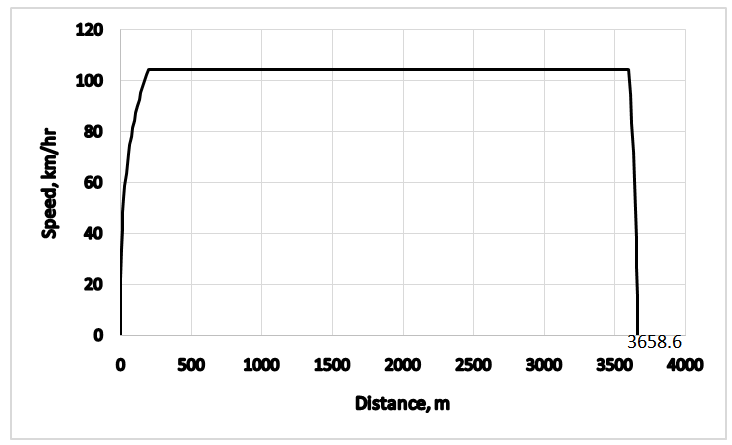
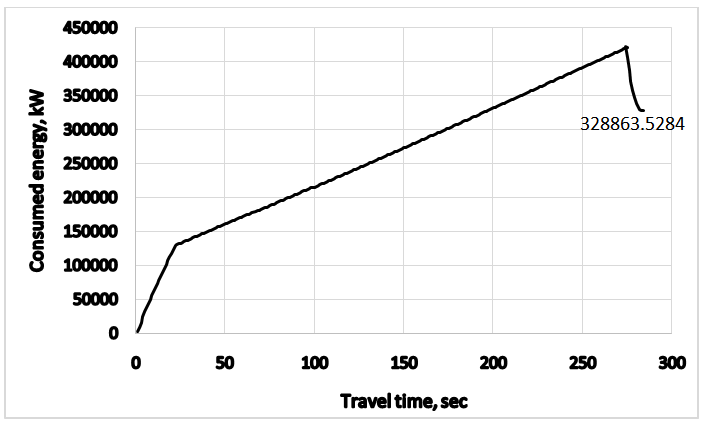
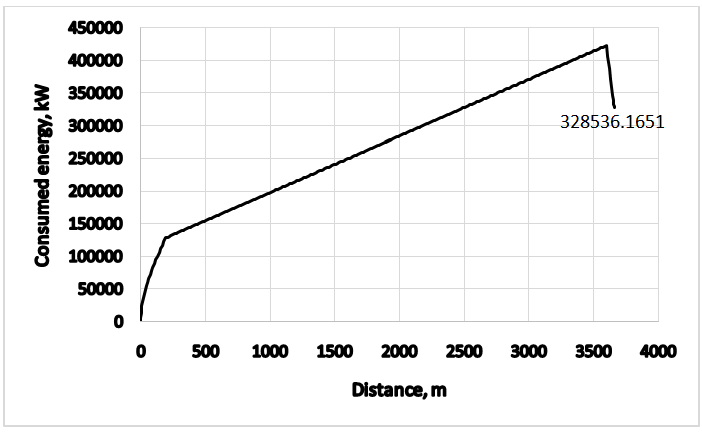
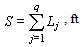
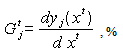
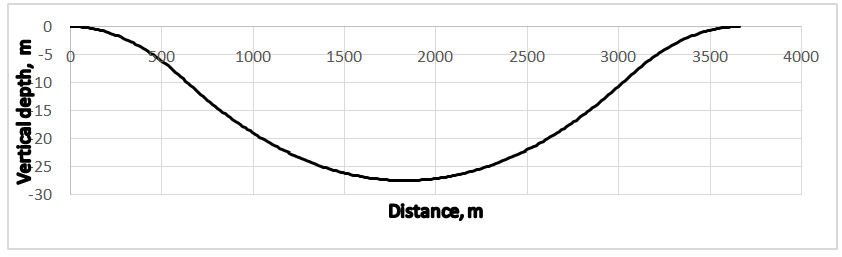
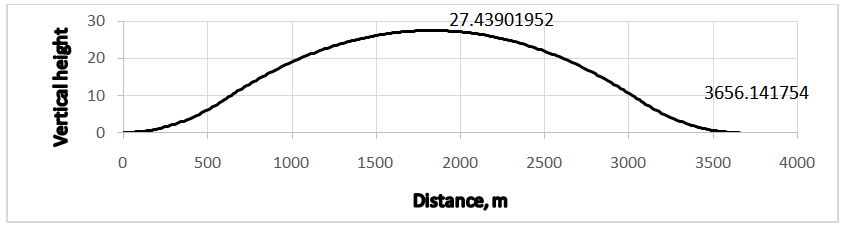
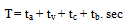
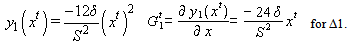
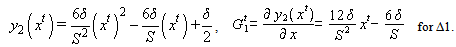
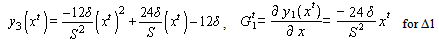
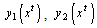 and
and 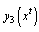 represents elevations with respect to xt in metres on different segments, while
represents elevations with respect to xt in metres on different segments, while 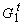 is the gradient at xt in percent, and Δ1, Δ2, Δ3 are 1/6, 2/3 and 1/6 of S, respectively (Fig. 11).
is the gradient at xt in percent, and Δ1, Δ2, Δ3 are 1/6, 2/3 and 1/6 of S, respectively (Fig. 11).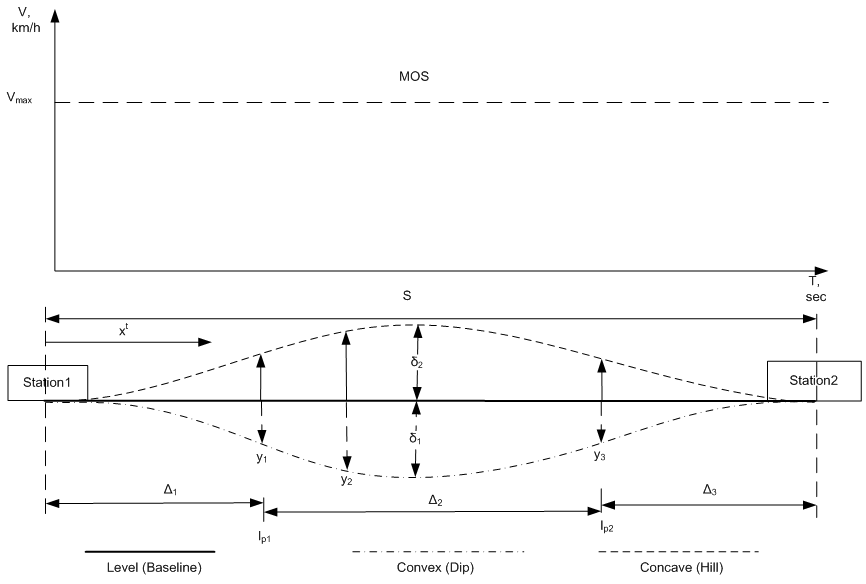
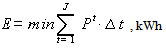 Subject to
Subject to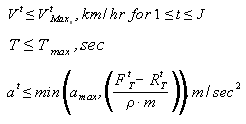
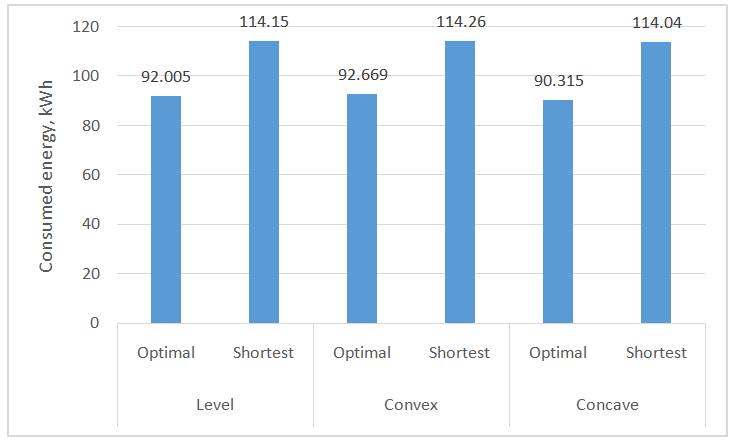
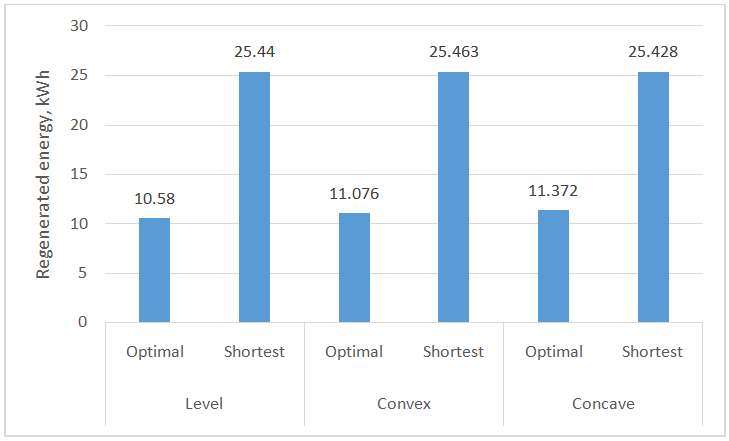
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML