1. Introduction

1.1. Background

The urban population and number of vehicles are increasing rapidly day by day and causing problems in road traffic movement which affect various human activities. Due to growth of population in cities, demand of utility commodities is also increasing day by day, so there is a need for the fleets of vehicles to deliver goods and material to the customers within minimum time and cost frame by covering shortest distances to cover each customer once. In any city, road network is the backbone of the circulation within city for the delivery of goods and services. There can be various types of road networks which have been developed in cities, linear, organic, grid iron, radial are some of them. Road networks play an important role in the development of the city and an efficient network provides optimum travel time and distance to the user from origin to the destination.

The class of vehicle routing problems addresses situations characterized by a variety of operational characteristics, such as the type of distribution, service nature, constrained customer visiting duration and routing time, vehicle capacity limitations, and restricted types of vehicles for serving specific customers. Such diversity of variants and their inherent difficulty justifies the intense research effort and numerous reports comprising surveys of problem classification, solution methods and applications of vehicle routing.

Road network is basically a system of interconnected linear (Roads) and point (junctions/intersections) features through which vehicles are moving and this can be represent in terms of graphs. All the point and line features can easily be represent in geographic information system in referenced way. Remote Sensing (RS) and Geographic Information System (GIS) technologies have the capability to solve the network related problems such as optimal path finding, closest facilities searching, service area analysis, travelling sales man problem, vehicle routing problem. All the real world restrictions, limitations and constraints can also be handled very easily with the help of GIS technology.

In this study we have used the capabilities of RS and GIS technologies to handle the vehicle routing problem in Dehradun city for the delivery of goods and material from main distribution centre to the local store keepers (customers). The main interest of this study is to incorporate the multiple vehicles, capacity of each vehicle and also the time preferences of each customer (time window) in the solution of VRP using Tabu search algorithm in GIS environment and finally find out the results in the form of maps with proper travel directions of routes of vehicles.

Digital database creation of road transportation network for MDCVRPTW in GIS, analysis of MDCVRPTW using Tabu search algorithm by considering multiple parameters in GIS environment, and finally generate the results in map form with proper routes and travel directions of every vehicle, are the main objectives of this study. In this study multiple parameters like customer demand in terms of type of material and time, service time, waiting time, violation time, vehicle capacity, vehicle type, multiple-distribution centres, trip duration, lunch break during the trip, travel restriction over areas, time window at stores, type of delivered material, time impedance, distance impedance, over time servicing have been considered to perform the MDCVRPTW.

The potential challenges in obtaining the solution of MDCVRPTW in GIS environment using Tabu search algorithm are like what are the essential attributes of the transportation network (includes line and point features) and Network Dataset to find out the solution of MDCVRPTW and how can these be incorporated in the analysis using GIS technology? If the carrying capacity of the vehicles is varying then how the Tabu search algorithm handles this situation? If the total time span for the services is very large (since morning to evening), then the drivers also want to take a lunch break in between the journey, so how this lunch break can be incorporated in the solution of MDCVRPTW? Apart from these if any particular location or area is blocked temporary or permanently then how the vehicle routes are affected under this situation?

1.2. Multi-Depot Capacitated Vehicle Routing Problem with Time Window (MDCVRPTW)

Vehicle Routing Problem (VRP) is an important problem in the fields of road transportation, distribution and logistics in the context of delivery of goods or materials located at the central distribution centre (depot) to geographically scattered customers (stores). Since each vehicle has its own carrying capacity so this normal VRP is called Capacitated Vehicle Routing Problem (CVRP). The capacitated vehicle routing problem with time windows (CVRPTW) is an extension of CVRP in that each customer location must be served by a vehicle within a certain given interval of time (time window). The multi-depot capacitated vehicle routing problem with time window (MDCVRPTW) is the further extension of CVRPTW in that there are more than one central distribution centres (depots) to serve the customers. This MDCVRPTW is very frequently used in making decisions for the distribution of goods and services.

This problem involves a fleet of vehicles starting from the depots to serve a number of customers only and only once at different geographical locations along with various demands and within a specifictime windows before coming back to the same depot. The main objective of this problem is to find routes for all vehicles to serve all customer locations only once at a minimum total delivery cost (in terms of travel distance and time) without violating each time window set by customers at customer location and carrying capacity of vehicle. In this study the optimal solution of MDCVRPTW is carried out using Tabu search algorithm in GIS environment under without violation of above mentioned constraints.

For better understanding to this problem, a practical example with three depots and fifteen customers is illustrated in Figure 1. In this figure the values in the dotted box beside the depots represents the name of the depots, type of material which is delivered to the customers, type and number of vehicles available at the depots, total allowed trip time and the capacity of each vehicle. The values in the dotted box beside the stores represents the number of store, violation time by the vehicle, demand of material, delivery duration (time window), service time and type of demanding material at that store.

In this study we have three depots having different materials to deliver to the store through vehicles of same as well as varying capacity. The stores also have the varying demand in terms of type of material, quantity and time.

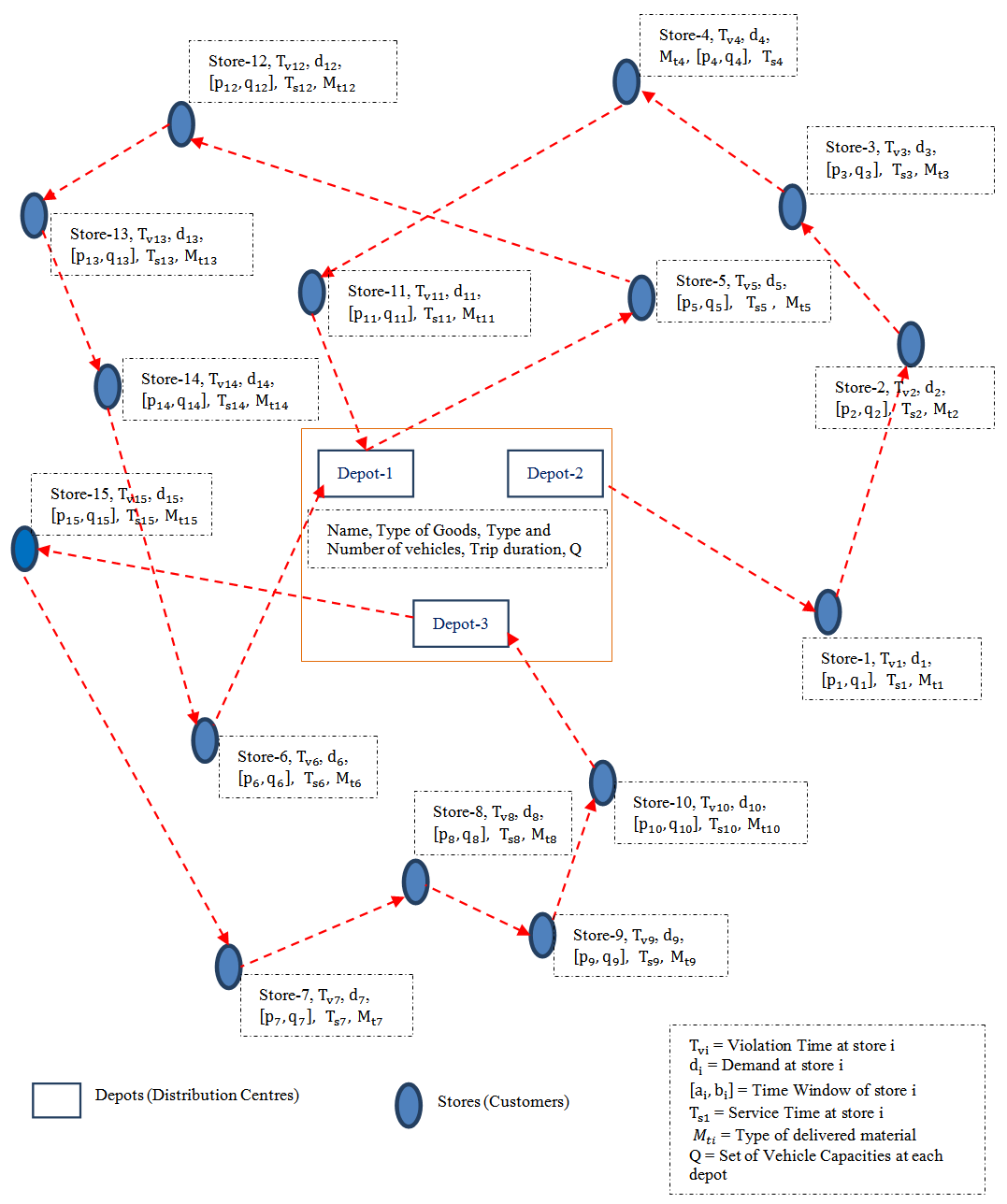Figure 1. Example of MDCVRPTW

1.3. Mathematical Formulation of Multi-Depot Capacitated Vehicle Routing Problem with Time Window

In the context of graph theory the MDCVRPTW can be defined by a directed graph G = (N, A) where 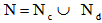is the set of nodes with 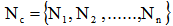is the set of n customer locations (stores), 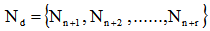is the set of r depots, and 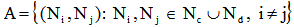is the set of arcs, satisfying the condition that all the routes of vehicles will start and end at the same depot.

A cost 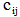(travel distance) and travel tim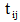e where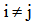, are assigned with each arc 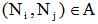of the road network, and the non-negative demand 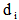and non-negative service time (delivery time or time window) 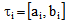are associated with each customer location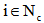. Let a set of m vehicles is 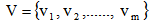and corresponding set of non-negative carrying capacity of each vehicle is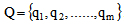. Let 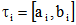is the loading time (depot time window) for each vehicle at the depot location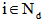, and D is the total allowed time span (trip time) of complete service by all the depots in a day.

At each customer location, the service must be start within the given interval of time, called a time window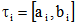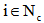. The vehicle is allowed to reach the customer location before the opening of the time window, and wait at no cost until service becomes possible, but it is not permitted to arrive after the latest time window.

A route R is characterised by the set of customers it contains. Hence for this two coefficients are defined as

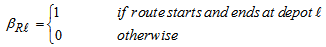If F represents the set of all possible route R satisfying

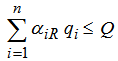(1)

and

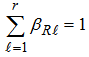(2)

Our formulation for MDCVRPTW uses three binary decision variables as follows

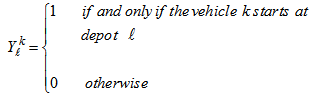and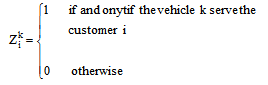

Let define the parameter and are the travel time of the vehicle on route R and total time (travel and service time at customers on that route) of route R respectively. If the route R starts and ends at the same depot then the parameter 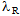can be obtained by solving the travelling salesman problem only on the nodes of route R. Thus the 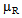can be written as

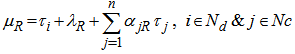Here the main objective is to find out a route set of minimal cost, only one for each vehicle in such a way that every customer is served only once. All the routes must be feasible with respect to the time windows of customers serviced and the carrying capacity of vehicles.

Mathematically the MDCVRPTW using Tabu search algorithm can be stated as-

Minimization conditions

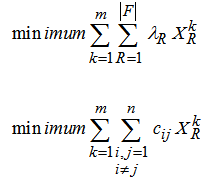(3)

With regard to

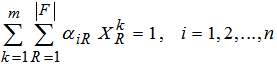(4)

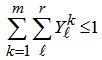(5)

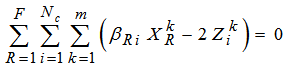(6)

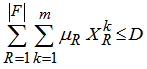(7)

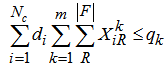(8)

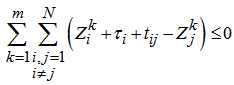(9)

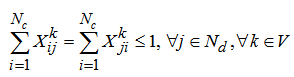(10)

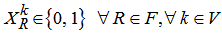(11)

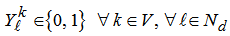(12)

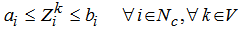(13)

The objective function (3) states that the total costs should be minimized in terms of travel distance and travel time. Constraints set (4) states that each customer location must be visited exactly once, while constraints set (5) make sure that at most one rotation is assigned to one vehicle. The constraints set (6) ensures that when a vehicle goes to an intermediate customer location, it also leave that customer location. Constraints set (7) ensure that the total duration of a rotation of a vehicle, and constraints set (8) impose that no vehicle can serve more customers than its capacity permits.

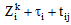The constraints set (9) states that the vehicle k cannot arrive at j^th customer before if it travels from i^th customer to j^th customer. Constraints set (10) guarantee that every route starts and ends at the same depot location. Constraints sets (11) and (12) represent the integrity constraints. And finally the constraints set (13) ensure that all time windows of customers are respected.

2. Litrature Review

Because MDCVRPTW is a very complex problem in the context of road transportation so only small instances of the MDCVRPTW can be solved exactly, it is clear that one cannot expect to solve the MDCVRPTW with the above formulation. We have therefore opted for the development of a Tabu search (TS) algorithm. This choice is motivated by the success of TS for the classical VRP and the MDVRP [14].

A lot of research has been carried out in the field of logistics, from the traveling salesman problem to complex dynamic routing problems. Among the prominent problems in distribution and logistics, the vehicle routing problem and its extensions have been widely studied for many years, mainly because of their applications in real world logistics and transportation problems. The time of the VRP solution grows exponentially with increasing the distribution points.

In this section, we will describe our algorithmic approach for the MDCVRPTW. It is based in part on the adaptative memory principle proposed by Rochat and Taillard [15] where solutions are created by combining elements of previously obtained solutions. Here single-depot and multi-depot routes will be combined, these routes will be generated by means of a Tabu search applied to three types of problems resulting from the decomposition of the MDCVRPTW into an MDVRP, VRPTW and CVRP sub-problems. In an MDCVRPTW problem, a set of minimal cost routes are generated on a network composed of customers and more than one depot, where each route starts and ends at the same depot.

Our Tabu search is based on the TS heuristic proposed by Cordeau et al. [16] which has proved highly effective for the solution of a wide range of classical vehicle routing problems, namely the Periodic VRP, the MDVRP as well as extensions of these problems containing time windows [17]. We now recall the main features of this heuristic.

Neighbor solutions are obtained by removing a customer from its current route and reinserting it in another route by means of the GENI procedure [18]. In the MDCVRPTW, insertions can be made in a vehicle associated with the same depot and same type of delivery goods or material.

To implement Tabu tenures for the VRP a set of attributes 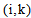indicating that customer 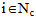is on the route 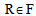of vehicle 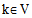is first defined. Whenever a customer 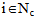is removed from route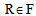, attribute 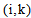is declared Tabu, and reinserting customer 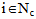in route 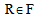is forbidden for a fixed number of iterations. The MDVRP works with attributes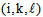, meaning that customer 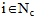is on the route 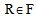of vehicle 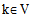from depot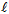. The Tabu status of an attribute is revoked if the new solution is feasible and of minimum cost than the best known solution having this attribute.

To broaden the search, infeasible intermediate solutions are allowed by associating a penalized objective f(s) to each solution s. This function is a weighted sum of three terms: the actual solution cost c(s), the violation q(s) of the capacity constraints, and the violation t(s) of the duration constraints. The global cost function is then f(s) = c(s) + a q(s) + b t(s), where ‘a’ and ‘b’ are positive parameters dynamically updated throughout the search. If the solution is feasible the two functions c(s) and f(s) coincide. This mechanism was first proposed by Gendreau et al. [19] in the context of the VRP. It allows the search to oscillate between feasible and infeasible solutions and enables the use of simple neighborhoods which do not have to preserve feasibility.

Several algorithms are available in the literature for the solution of VRP. Because this is a hard combinatorial problem, exact methods tend to perform poorly on large size instances, which is why numerous heuristics have been developed in the different studies. These include classical heuristics such as construction and improvement procedures or two-phase approaches, and meta-heuristics like simulated annealing, genetic algorithm, variable neighborhood search and evolutionary algorithms as in [20], [14] and [21].

In some contexts, one can assign more than one route to a vehicle. The Vehicle Routing Problem with Multiple Use of Vehicles (VRPM) is encountered, for example, when the vehicle fleet is small or when the length of the day is large with respect to the average duration of a route. The first heuristic was probably proposed in [22] for this problem. It is based on the savings principle for route construction combined with a bin packing procedure for the assignment of routes to the vehicles. Again using a bin packing procedure for assigning routes to vehicles an adaptive memory and a Tabu search heuristic have developed in [23]. Other heuristics have been proposed for the VRPM, such as those of [24] and [25] based on Tabu search or, in the ship routing context, the methods proposed in [26] and [27] which create routes by solving traveling salesman problems (TSPs) and solve an integer program for the assignment part.

Another well-known generalization of the VRP is the Multi-Depot Vehicle Routing Problem (MDVRP). In this generalization every customer is visited by a moving vehicle based on one of several depots. In the standard MDVRP every vehicle route must start and end at the same depot. There exist only a few exact algorithms for the solution of this problem. The exact branch-and-bound algorithms have been developed in [28] and in [29] but these only work well on relatively small instances. Several heuristics have been put forward for the MDVRP and early heuristics based on simple construction and improvement procedures have been developed by several authors in [30], [31], [32], [33], [34], [35], [36].

More recently, a search procedure have been proposed in [37] with combining the [10] for record-to-record local method for the reassignment of customers to different vehicle routes, followed by [38] for the improvement of individual routes. A Tabu search heuristic has described in [39] in which an initial solution was built by first assigning every customer location to its nearest depot. A petal algorithm developed by [40] is then used for the solution of the VRP associated with each depot. The Tabu search approach of in [16] is probably the best known algorithm for the MDVRP. An initial solution is obtained by assigning each customer to its nearest depot and a VRP solution is generated for each depot by means of a sweep algorithm. Improvements are performed by transferring a customer between two routes incident to the same depot, or by relocating a customer in a route incident to another depot. Reinsertions are performed by means of the GENI heuristic [18]. One of the main characteristics of this algorithm is that infeasible solutions are allowed throughout the search. Continuous diversification is achieved through the penalization of frequent moves.

The Multi-Depot Capacitated Vehicle Routing Problem with Time Window (MDCVRPTW) has not received much attention from researchers. A simplified version of the problem is discussed in [41] and [42], in these they assumed that customer demands are all equal to Q and that inter-depot routes consist of back-and-forth routes between two depots. This problem is transform into a matching problem using greedy algorithm by the authors. Angelelli and Speranza [43] have developed a heuristic for a version of the Periodic Vehicle Routing Problem (PVRP) in which replenishments at intermediate depots are allowed. Their algorithm is based on the Tabu search heuristic of [16]. A version of the problem where time windows are considered is proposed in [44].

Our interest in the MDCVRPTW problem arises due to the distribution of different type of materials like Grocery, electronics & Electrical, Bakery and Cold Drinks item from three types of distribution centres (multi-depot) by multiple vehicles (three, four and six wheeler) of varying capacity in the a part of Dehradun city area. Several similar applications are encountered in the context where the route of a vehicle can be composed of intermediate stop (Lunch break) in order for the vehicle to be replenished. Our aim is to develop a Tabu search for the MDCVRPTW and to introduce a set of benchmark instances for this problem.

3. Study Area

A part of the capital city Dehradun of Uttrakhand state, has been taken as the study area for this study. It is located between the parallel 30° 17’ 31.63” N to 30° 17’ 31.63” N and meridian 78° 1’52.87” E to 78° 3’45.38” E, and at an altitude of 640 meters above the mean sea level. The total area covers approximately 10.0 sq. km., and shown in Figure 2.

Figure 2. Study Area

4. Materials and Methods

4.1. Satellite Data Used

In this study, the IKONOS satellite (launched date 24^th Sep, 1999) data is used for the preparation of digital database in GIS environment for MDCVRPTW. IKONOS satellite image is of high spatial resolution (Nadir: Panchromatic 0.82 ms & Multispectral 3.2 ms; 26⁰ off Nadir: Panchromatic 1 m & Multispectral 4.0 ms) and used in the development plan of city for identifying to roads, and other urban features.

4.2. Field Data Acquisition

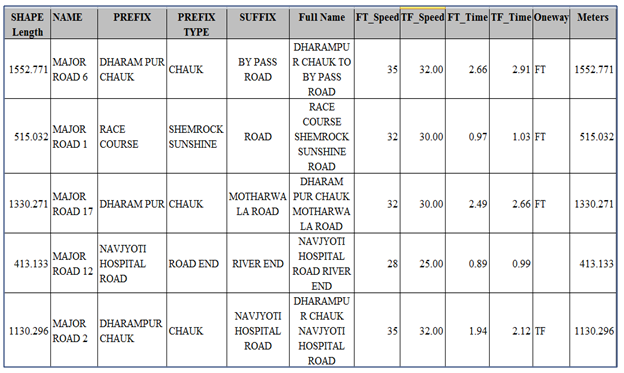
In addition to satellite data we have collected field data of various locations of distribution centres and stores in our proposed study area using hand held Garmin GPS. At the same time the attribute information for distribution centres and stores is also collected from the field. Table 1 shows the attribute field data which was collected from field survey.

Table 1. Attribute data of Distribution Centres and Stores Locations Related Information Three Distribution Centres Name, Type of Material, Number and type of Vehicles, Capacity of Vehicles, Trip time (Time Window), Service Time (loading time), Latitude & longitude 39 Stores Name, Product Demand, Time Window, Service time, Violation Time, Latitude & longitude

4.3. Software Used

In this study, ESRI desktop product ArcGIS 10.0 software is used for the creation of GIS database, spatial and non-spatial data entry and editing, topology creation, network dataset creation, MDCVRPTW analysis and finally generating the maps of MDCVRPTW results along with the travel directions of each vehicle.

4.4. Methods Used

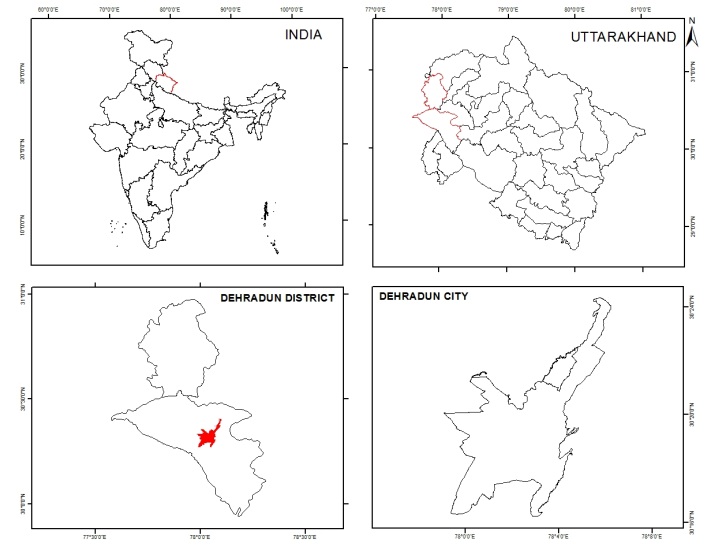
The method used in this study is explained in the form of a flow chart (Figure 3). It is further described under various heads mentioned below.

Figure 3. Flow Chart of Methodology

4.4.1. Flow Chart

The flow chat of methodology adopted in this study is shown in Figure 3.

4.4.2. Database Creation

Creation of database is important part for the analysis, here geo-referenced IKONOS satellite image with WGS_1984 Datum, UTM Projection and 44 N Zoneis used for preparing database in GIS environment. Personal geo-database has been created with feature class dataset and feature classes in the same coordinate system as the satellite image. To store the spatial information in this database, we have created major roads, minor roads and streets as the line features, depots (distribution centres) and stores (customer locations) as the point features. To manage the non-spatial information about all the point and line features for the requirement of analysis of MDCVRPTW, different attribute fields and their data types for line and point features have been created, these fields are shown in the tables 2, 3 & 4.

Table 2. Attributes of Line Features S. No. Attribute Fields Data Type 1. Object ID Short Integer 2. Shape Text 3. Shape Length Double 4. Meters Double 5. FT-Speed Short Integer 6. TF-Speed Short Integer 7. FT-Minutes Double 8. TF-Minutes Double 9. One way Text 10. Prefix Text 11. Prefix type Text 12. Suffix Text 13. Suffix type Text 14. Full names Text

Table 3. Attributes of Distribution Centre S. NO. Attribute Fields Data Type 1. Object ID Short Integer 2. Shape Text 3. Name Text 4. Material_type Text 5. Vehicles_Type Text 6. Vehicle_Capacity Long Integer 7. Number_Vehicles Short Integer

Table 4. Attributes of Stores S. No. Attribute Fields Data Type 1. Object ID Short Integer 2. Shape Text 3. Name Text 4. Demand_EE,Demand_Bakery, Demand_Gro_CDrink Short Integer 5. Service_time_EE, Service_time_Bakery, Service_time_Gro_CDrink Short Integer 6. Start_time_EE, Start_time_Bakery, Start_time_Gro_CDrink Date 7. End_time_EE, End_time_Bakery, End_time_Gro_CDrink Date 8. Demand_Product_Type Text 9. Violation_time_EE, Violation_time_Bakery, Violation_time_Gro_CDrink Short Integer

4.4.3. Spatial and Non-spatial Data Entry and Editing

In spatial data entry part, the spatial information of line features have been entered by means of digitization in GIS environment over satellite image, and point features have entered using coordinates values (latitude and longitude) which is collected from the study area during field survey using GPS. To fulfill the requirement of the road network analysis, we have edited the nodes (vertices) and also modified the shape of the line feature for better connectivity among the features.

The non-spatial data entry is indicates the attribute information of all features of all feature classes. For line feature classes, the attribute information as shown in table 2 are entered into the attribute tables of corresponding feature classes. The attribute information for point feature classes have entered into the attribute tables of these feature classes according to table 3 & 4.

For line features we have used the time as well as distance as the cost functions (impedance factor) for the analysis of MDCVRPTW. For this we first collected the maximum allowed speed on the individual line feature and using this speed and length of line feature the travel time is calculated for each line feature. In our study we have introduced this allowed speed as well as travel time for both the directions that is from-to (FT, along the digitizing direction) and to-from (TF, opposite to the digitizing direction) speeds and travel times.

Mathematically, the travel time cost function can be written as

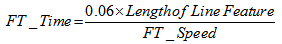(14)

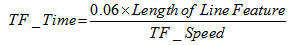(15)

Here the unit of travel times, length of roads and speed on the roads is in minutes, meters and kilometre per hour respectively.

4.4.4. Creation and Validation Network Topology

To overcome the problems of connectivity and continuity among the line and point features during digitization, we have created feature dataset based network topology of all point and line feature classes. During network topology creation we have added the following topological rules keeping cluster tolerance 0.001 meters.

1. Distribution_Centres must not disjoint

2. Stores must not disjoint

3. Major_Roads must not overlap

4. Major_Roads must not overlap with Minor_Roads

5. Major_Roads must not overlap with Streets

6. Minorr_Roads must not overlap

7. Minor_Roads must not overlap with Streets

8. Streets must not overlap

9. Major_Roads must not have dangles

10. Minor_Roads must not have dangles

11. Streets must not have dangles

4.4.5. Network Dataset Creation for MDCVRPTW

Network dataset is a set of all vertices and edges which stores all the line and point features together for performing the network related problems in ArcGIS software. To solve the MDCVRPTW we have created a network dataset of all the line and point features. The main elements of network dataset are connectivity, turns, attributes and direction. In this study we have decided any vertex connectivity policy to connect all linear features at any possible vertex and override connectivity to connect all point features to its nearest line feature.

In case of turn we have chosen the all possible turn (global turns) at a roundabout or intersection of line features. For network attribute, three types of attribute have been created in which two ‘Travel_Distance’ and ‘Travel_Time’ are cost type attributes and one ‘Oneway’ is restriction type of attribute.

To get better output in term of proper travel directions of vehicle route from the distribution centre to the concerned stores to the same depot we have assigned the direction fields Prefix, Prefix type, suffix, suffix type and full name of each and every line feature in the network dataset.

4.5. Modes of Transport Used

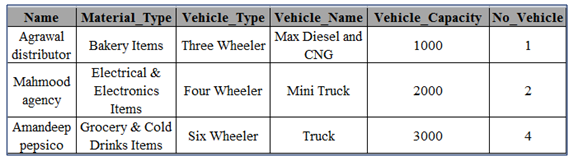
The mode of transportation is also important in the field of transportation and logistics. In our study area only road transportation is allowed and following types of vehicles are used for the delivery of goods and material as.

a) Truck (Six wheeler)

b) Mini truck (four wheeler)

c) Max Diesel & CNG (three wheeler)

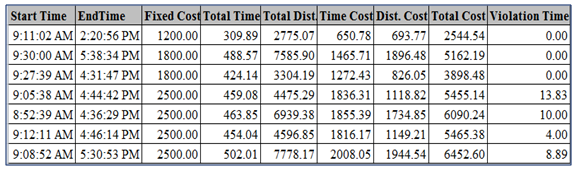
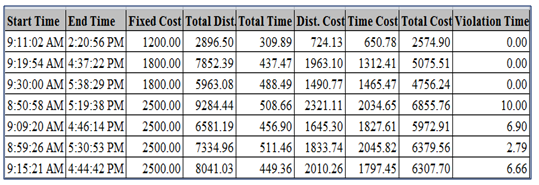
5. Results and Discussions

In this section the results of MDCVRPTW are shown in various heads based on multiple parameters and attributes related to distribution centres and stores like type & capacity of vehicles, time window of each store, total trip time, cost function, demand and service time at each store etc. In each head, we vary types of these input parameters and observe the vehicle routes.

This section explains the sensitivity analysis of different parameters and attributes as well as computational results. We first describe how the complete dataset and hence the network dataset and vehicle routing analysis layer have been generated? Finally, GIS results of MDCVRPTW using Tabu Search algorithm are presented in the Map forms with proper travel directions, travel distance and travel time followed by discussion.

5.1. GIS Database and Network Dataset

The complete GIS digital database containing point and line features of the study area are shown in Figure 4.

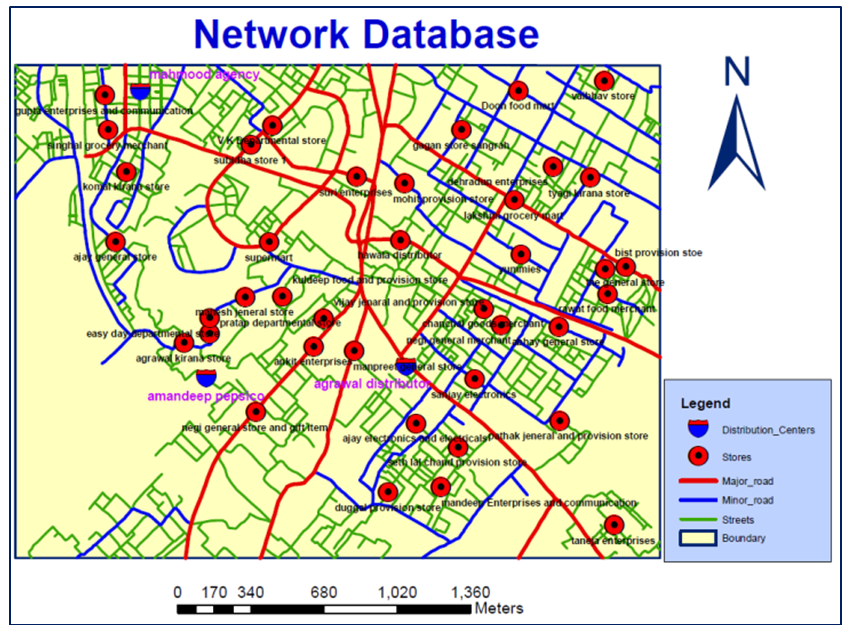Figure 4. GIS Spatial Database of Study area

The required attribute information associated withline and point features for the solution of MDCVRPTW are shown in Table 5 & 6.

Table 5. Attributes of Major Roads

Table 6. Attributes of Distribution Centres

Here the shape Length and Meters attribute fields represents the length of major road in meters, Name field represents name of major road, PREFIX & SUFFIX represent the what is at the starting and end of the major road, Full Name is name of road name followed by its prefix and suffix, FT_Speed & TF_Speed and FT_Time & FT_Time are the maximum allowed speeds (in km/h) & travel times (in minutes) of the vehicle on the major roads along the (From-To) and reverse (To-From) direction of digitization. In ‘Oneway’ field FT and TF represent the vehicle movement is restricted along (FT) and reverse (TF) direction on that road respectively i.e the road is one way, however, blank entry in this field does not restrict the movement of vehicle in any direction.

In this GIS database there are total three distribution centres (depots), 39 customer locations (stores), 594 streets, 53 minor roads and 25 Major roads.

The geodatabase based network dataset for the analysis of MDCVRPTW is shown in Figure 5. This network dataset has edges (line) and junctions (points) features in it with 1131 junctions.

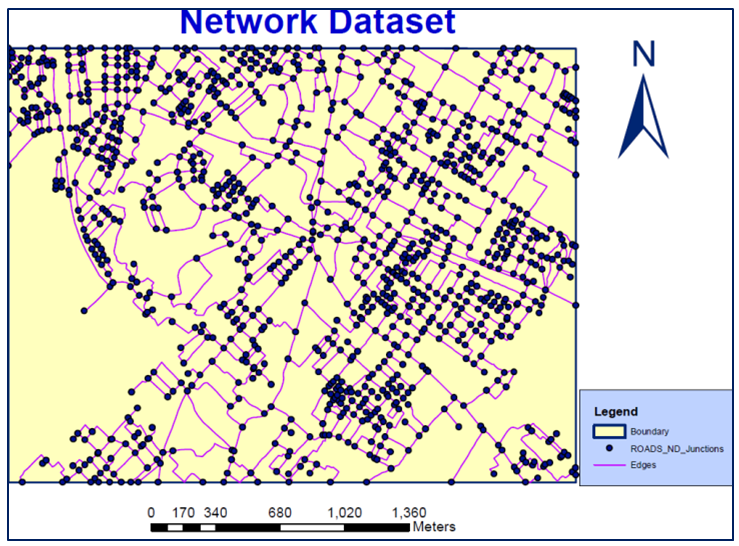Figure 5. Network Dataset of Network Database

Once the network dataset is built, we are ready to perform the analysis of MDCVRPTW. In the network analyst toolbar after checking the network analyst extension we have chosen the vehicle routing problem (VRP) layer and then loaded all the distribution centres and stores and decides the routes of all the vehicles.

5.2. Distribution of Bakery, Electrical & Electronics, and Grocery & ColdDrink Items

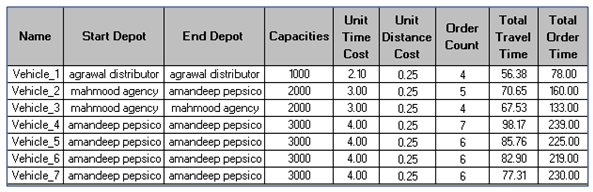
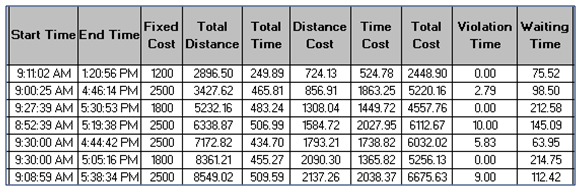
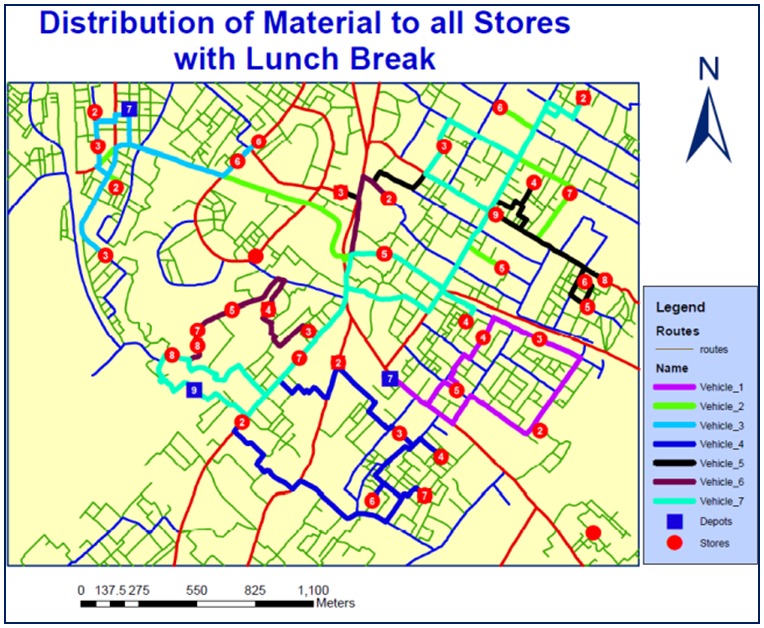
In this part the distribution of Bakery items from Agrawal distributor, Electrical & Electronics (EE) items from Mahmood Agency, Grocery & Cold drink items from Amandeep pepsico is analysed to all the stores according to their requirements. For this, all the customer locations (stores) are assigned to the orders, distribution centres to the depot of VRP analysis layer. The routes of all seven vehicles are predefined under routes layer by the names vehicle_1, vehicle_2 and so on. In this study multiple parameters for vehicle (like start & end depot names, vehicle capacity, fixed vehicle cost, cost per unit time & distance, number of order count etc.), for store location

(Stores name, service time, start time Window, end time Window, maximum violation time and deliveries quantities) and for distribution centres (name, time window, loading time etc.) have been assigned. The trip time for each distribution centre is since 8:00:00 AM to 5:30:00 PM. These types of multiples inputs have not been considered in other studies yet. Figure 6 shows the routes of all vehicles e.g. route of vehicle from the distribution centre to all covered customer location and finally return back to their respective distribution centre. The routes of all the vehicles are shown by different colour under legend in Figure 6.

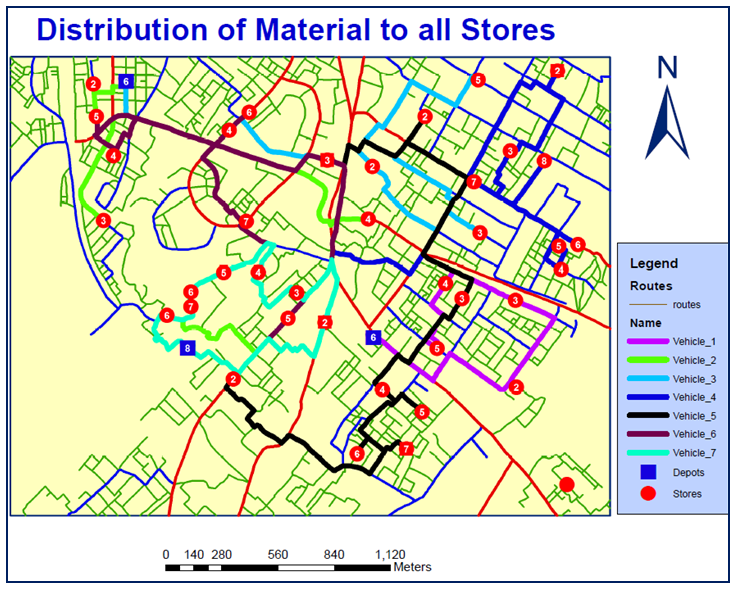Figure 6. Route of all Vehicles

Table 7a & 7b shows the route parameters like total distance travelled, total travel time, cost per unit time & distance, total coat, total violation time, total service time etc. at customer locations for each vehicle.

Table 7a. Attribute information of all the Vehicles (Part A)

Table 7b. Attribute information of all the Vehicles (Part B)

The proper direction of movement of the vehicle from associated distribution centre to all associated customer locations and finally come back to associated distribution centre for all the vehicles can be shown under driving directions. Figure 7 shows the driving directions of vehicle 1according to which vehicle 1 stats from Agrawal distributor (having time window 8 AM – 5:30 PM and service time of 40 minutes) and goes east on street13 toward street12 within 1 minutes of time (and 14 meters distance) and then takes right turn on Dharampur Chauk Navjyoti Hospital Road and again moves 362.4 meters distance, the rest path is shown in the Figure 7. By this way vehicle starts at Agrawal distributor and serves associated stores and then finally returns back to the Agrawal distributor without violating its capacity and time window constraints.

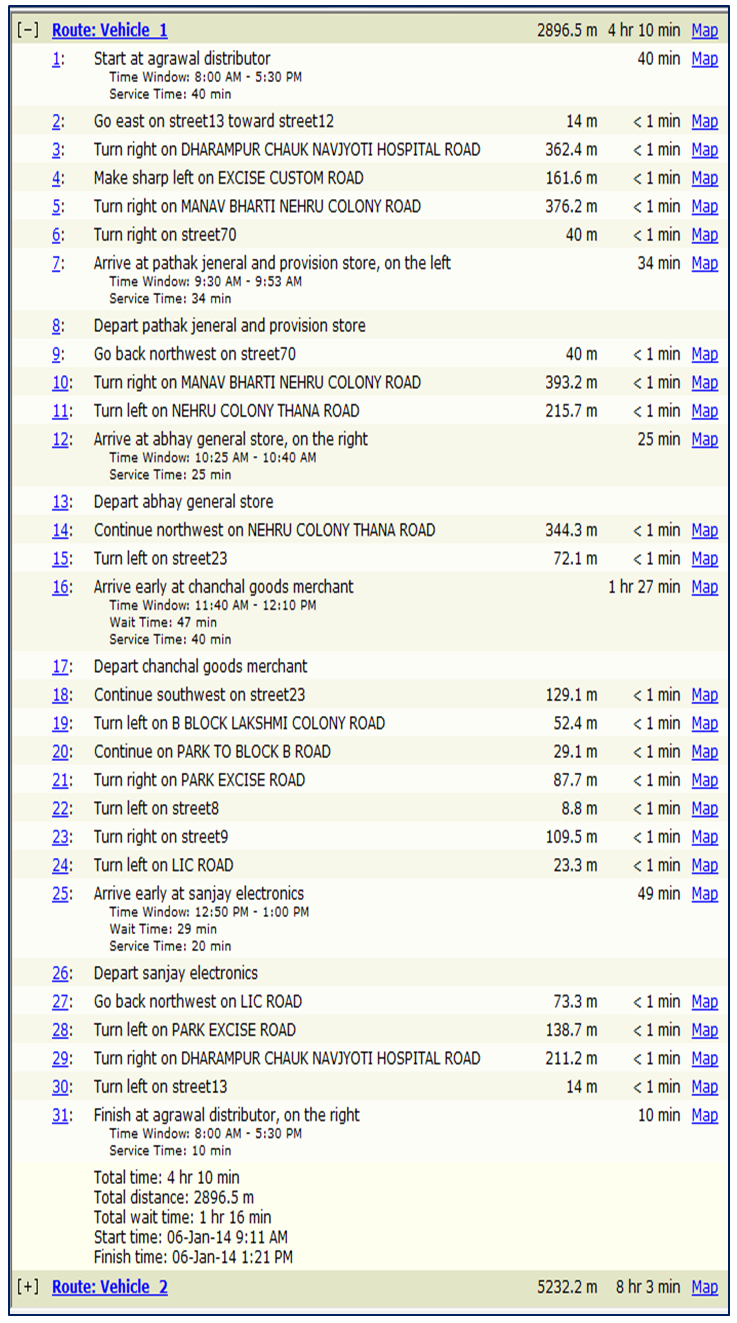Figure 7. Driving direction of Vehicle 1

Here all the customer locations are served by the vehicles in near optimal transportation cost by keeping multiple customer demands into consideration and without violating any constraint.

5.3. Distribution of All Type of Material to All Stores along with Lunch Break

In order to handle important situation associated with vehicle drivers during delivery of the material. When the driver works from morning to evening to supply the material, they want to take break for lunch during trip. In this situation we decided to give one hour break for lunch in between the total trip duration and also incorporate it to the solution of MDCVRPTW.

In addition to all parameters considered in 5.2, here lunch break for all the drivers of all the seven vehicles during the trip (8:00:00 AM to 05:30:00 PM) is incorporated. Here the lunch break is allowed between 1:00:00 PM to 2:00:00 PM followed by 10 minutes of violating time and 20 minutes of maximum travel time. Figure 8 shows the routes of all vehicles followed by lunch breaks which are slightly changed from above results.

Figure 8. Route of all Vehicles

Table 8 depicts the attribute information about all the vehicle i.e. starting & ending journey time, fixed cost for hiring vehicle, total travel time & distance, cost according to travel time & distance, total delivery cost and violation time by the individual vehicle.

Table 8. Attribute of Vehicle Route

The Driving directions of vehicle 6 with complete information are shown in Figure 9. The vehicle starts from Amandeep pepsico and goes to different stores and stops for driver’s lunch break before 01:00:00 PM, and again starts to serve the other sotes and finally reachingAmandeep pepsico.

The lunch break is highlited in Figure 9 by the red circle in which the vehicle is waiting for 5 minutes for lunch. In this experiment the vehcle 6 is also violating the time window of kuldeep food and provision store by 4 minutes.

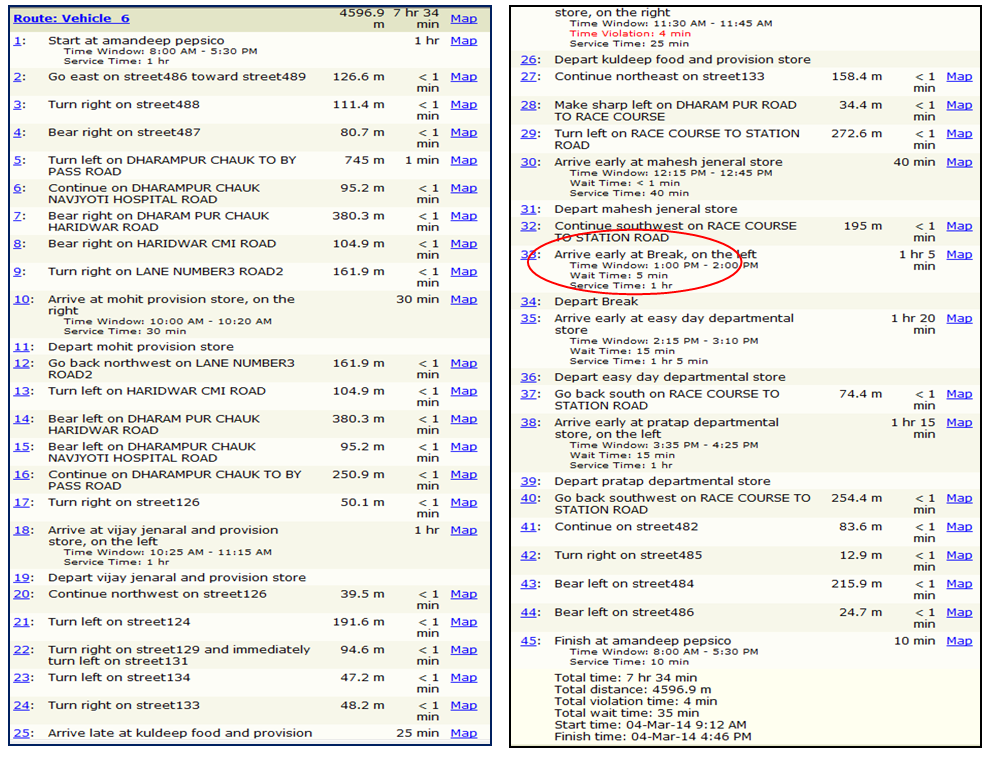Figure 9. Driving direction of Vehicle 6starting from Amandeep Pepsico

5.4. Distribution of All Type of Material to All Stores along with Lunch Break & Restricted Area

There are some areas in the city like cantonment area through which the movement of the vehicles is not allowed. These types of restricted areas can also be identified and thus vehicles chose their routes within the city except restricted areas. To tackle this situation polygon barrier have been around the restricted areas in addition to the parameters assigned in 5.2 and 5.3, and then solve the MDCVRPTW. The orange coloured area in the Figure 10 given below is blocked for the movement of vehicles and hence finally the routes of the vehicles are changed which are shown in Figure 10.

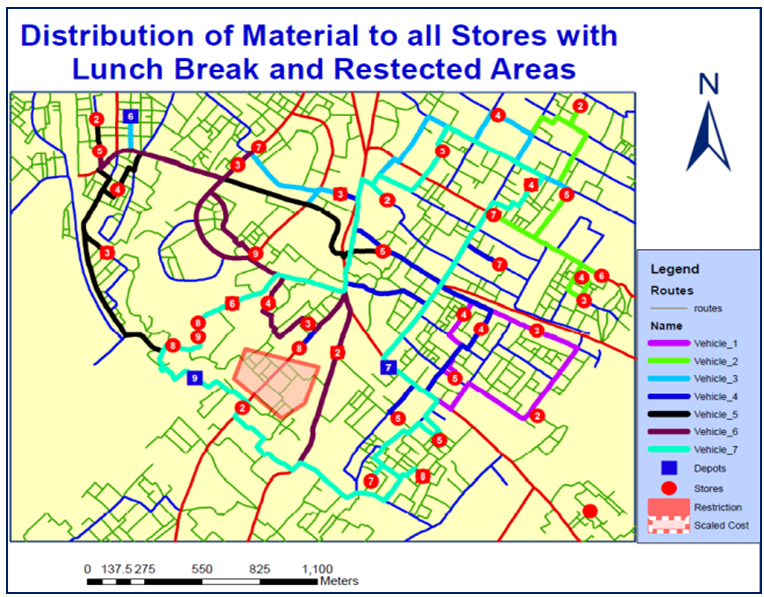Figure 10. Route of Vehicles

The attribute fields for the distribution of all types of material with lunch breaks and restricted areas are shown in table 9 below.

Table 9. Attributes of All vehicles routes

The Driving directions of vehicle 1 with complete information are shown in Figure 11. The vehicle starts from Agrawal Distributer and goes to different stores. The vehicle movement is in such a way that the restricted areas are avoided and finally reaching to the same distribution centre.

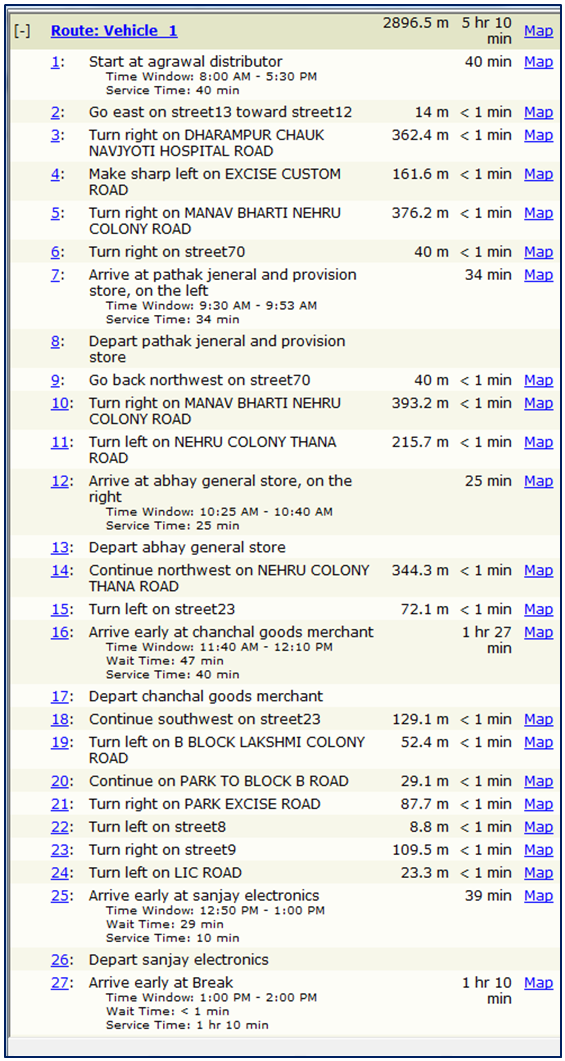Figure 11. Driving directions of Vehicle 1

This study is different from other studies in the following respects. (1) In other studies the vehicle is selecting the customer locations randomly but in this study the customer locations are selected according to the predefined time window of the customer location and allowed vehicle capacity. (2) There are other studies in which researchers considered only few parameters at a time for the solution of MDCVRPTQ while in this study we have considered multiple parameters at a single time and find out the near optimal solution of MDCVRPTW. (3) Our results are more significant because we have solved the MDCVRPTW using GIS technology which is very familiar in the academic, scientific and industrial domains.

6. Conclusions

The vehicle routing problem (VRP) is one of the most important combinational optimization problems that has nowadays received much attention because of its real application in industrial and service problems for distribution management. Several versions of problems exist and a wide variety of exact and approximate algorithms have been proposed for its solution. Exact algorithms can solve relatively small problem, but a number of approximate algorithms have been proved very satisfactory. Our Tabu search algorithm is also an approximate algorithm in which we have considered multiple parameters to get the approximate solution.

In this study we have proposed Tabu Search algorithm for the near optimal (approximate) solution of MDCVRPTW in which vehicles can be replenished at intermediate depots along their route. Thisproblem has applications notably in distribution of goods and material and their management. We have proposed a GIS based methodology on adaptive memory and Tabu search algorithm for the generation of a set of routes from distribution centre to set of customer locations.

In this study we have considered multiple parameters according to the actual requirement of the customers and also for the distributors. This type of transportation problem for the distribution of goods and material has very important significance for the urban transportation management and planning.

Tabu search exhibits a robust behavior and reasonably fast running times. Because the MDCVRPTW is a new problem, no previous statistics are available but we hope our results will enable other researchers to produce comparative results for this transportation problem.

In this study we discussed a GIS based solution approach tailored for the MDCVRPTW based on ant city optimization. The performance of the algorithm was judged to a Tabu search approach and discussed by means of computational experiments comprising 39 demand cluster points derived from classic VRPTW. The performances of the Tabu search algorithm was tested and found very well in terms of computation time and speed.

We conclude that the Tabu search algorithm scores very well on all dimensions in background with formulation techniques to solve the MDCVRPTW for different types of materials and got minimum cost with respect to time and distance.

Network analysis in GIS provides solution to vehicle routing problem for delivery and pickup of commodities. It is recommended as per the study carried out that GIS is an effective tool to search and select most suitable route for the optimum transportation cost with minimum travel distance. This can be applied in public distribution system of government, fleet management people, city bus routing, school bus routing, Wholesalers, Clearing and forwarding agents, traders and many such applications where vehicle routing problem is faced. There are various methods available in GIS which can be explored and compared for the most suitable result.

The road network problems are complex and cannot be handled effectively with traditional techniques which are cumbersome, demand more time involvement and also do not give multiple options for analysis and outputs, hence it can be recommended that professionals as well as government agencies should attempt GIS as innovative and customized tool to deal with vehicle routing problems.

The authors thank Director, Indian Institute of Remote for providing the transport facility for the collection of field data, useful references, and computer laboratory with standard software for data execution and analysis and all other supports. The authors are also thankful to Head of Geoinformatics Department of Indian Institute of Remote Sensing for his valuable comment and guidance in the writing of this research paper.