-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Traffic and Transportation Engineering
p-ISSN: 2325-0062 e-ISSN: 2325-0070
2013; 2(6): 149-158
doi:10.5923/j.ijtte.20130206.03
Evaluation of Travel Time Data Collection Techniques: A Statistical Analysis
Laura Berzina 1, Ardeshir Faghri 2, Morteza Tabatabaie Shourijeh 3, Mingxin Li 2
1McCormick Taylor, Inc., Newark, Delaware, USA
2Department of Civil & Environmental Engineering, University of Delaware, Newark, Delaware, USA
3I.S. Engineers, LLC, Houston, Texas, USA
Correspondence to: Mingxin Li , Department of Civil & Environmental Engineering, University of Delaware, Newark, Delaware, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Measuring traffic congestion is a key element of Congestion Management Systems (CMS) and is utilized to document traffic information and make decisions regarding existing traffic congestion problems. With the improvement of Global Positioning Systems (GPS) technologies, amongst other Intelligent Transportation Systems (ITS) components, various data collection procedures can be performed more efficiently. This paper examines travel time data collection methods. Data collection approach is introduced and a non-parametric statistical analysis of three different data collection methods, namely GPS, DMI (Distance Measuring Instrument), and MAN (manual), is conducted. The statistical analysis shows that the GPS approach is more consistent in terms of accuracy than the other two methods. The results also indicate that for short travel distances and trips without any delay, the three methods are accepted as being equal with a 95% confidence level. However, segment with different characteristics need to be investigated further through more data collection and analysis.
Keywords: GPS, Statistical analysis, Travel time and delay, Data collection, Accuracy
Cite this paper: Laura Berzina , Ardeshir Faghri , Morteza Tabatabaie Shourijeh , Mingxin Li , Evaluation of Travel Time Data Collection Techniques: A Statistical Analysis, International Journal of Traffic and Transportation Engineering, Vol. 2 No. 6, 2013, pp. 149-158. doi: 10.5923/j.ijtte.20130206.03.
Article Outline
1. Introduction
- Measuring traffic congestion provides the data that is used in decision-making towards congestion managementby documenting congestion information such as travel time, average speed, or delay time[1]. Travel time and delay data is perhaps the most important type of data used tocalibrate and validate the simulation model that supports Advanced Traveler Information Systems (ATIS) and Advanced Traffic Management Systems (ATMS) strategies for road capacity enhancement, such as traffic signal optimization and incident management on freeways and arterials[2-6]. Quiroga and Bullock[7] grouped the most commonly used techniques for collecting travel time data into two categories: roadside techniques and vehicle techniques. With improvement of GPS technologies, various travel time data collection procedures can be performed more efficiently. Data collection techniques for travel time and delay are usually organized in four general groups[8]:■ The active test vehicle technique■ The license plate matching technique■ The passive ITS probe vehicle technique■ New and non-traditional techniquesSince the 1920's, the test car technique has been used to collect travel time, and is still one of the most common methods. Using this technique the driver behaves like an average driver, without being below or exceeding the speed of an average vehicle in the stream of traffic. In this paper, the active test vehicle technique (also known as test vehicle technique or probe vehicle technique) is studied in three different levels of its own:■ Manual (MAN)- recording, manually, elapsed time at predefined control points■ The Distance Measuring Instrument (DMI)- determining travel time and distance along a corridor based upon speed■ The Global Positioning System (GPS)- provides test vehicle position, time, and speedThe use of traditional sensors installed on major roads (e.g. inductive loops, AVI sensors)[8][9] or more recent Bluetooth sensors[10] along arterials and freeways for collecting data is necessary but not sufficient because of their limited coverage and expensive costs for setting up and maintaining the required infrastructure[11]. Moreover, traditional sensors are capable of monitoring discrete points along the most congested roadway but do not provide information about conditions on the road sections between sensors. As a relatively low-cost, high accuracy solution, GPS related data collection techniques have gained acceptance among transportation engineers and practitioners [12]. Since1997, the Delaware Department of Transportation (DelDOT), with help from the Delaware Center for Transportation (DCT) at the University of Delaware, has been using the GPS technique to collect the travel time and delay data on all major roads and highways in the State of Delaware (Figure 1). Previous studies have proven that travel time data collection using the GPS is equally accurate as the manual test vehicle method, and that it is 50% less labor-intensive[13][14]. However, there is a lack of studies to compare the three techniques. A comparative analysis of manual and GPS techniques has shown with a 95% confidence level that the difference between the manual and the GPS technique is not statistically significant[13]. Using the parametric t-test and the F-test the variances were found to be equal and the means of the methods were not significant at the two-tailed probability level.This paper furthers this investigation and presents an extensive non-parametric statistical comparison of the data accuracies using GPS, DMI, and manual data collection techniques.
2. Experimental Data Collection Procedure
- The experimental data collection method includes the design of the process and data variables. First, about a four-mile long stretch of Route 896, south of Newark, Delaware was chosen, a map of which appears in Figure 2. The main purpose of choosing this particular section was to obtain a fewconsecutive segments,each with different characteristics, to test if the segment variables (length, number of signals, curves etc.) have an impact on travel time and delay time data collection methods.Distance on a two-lane arterial highway was divided into three segments in each direction, for a total of six segments (Table 1). Each of the three one-directional segments had slightly different characteristics: Segment 1 has a straight section with several traffic lights, Segment 2 is a stretch of road with one light in the southbound direction and with no delay in the northbound direction, and Segment 3 is a longer segment including four traffic lights and is curved at one end of the segment.
|
 | Figure 1. Example of route map output from GIS |
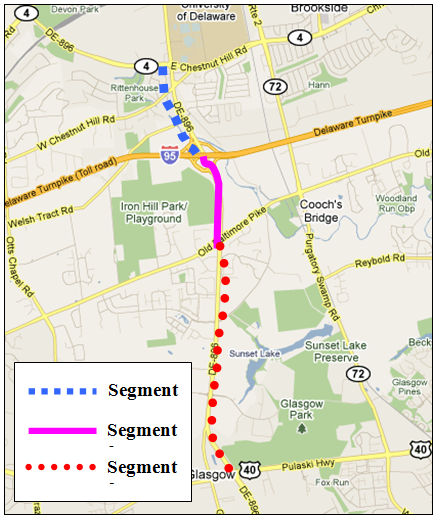 | Figure 2. The study area with three segments of the State Route 896, Newark, DE (Source: ©2013 Google Map) |
3. Statistical Analysis of the Data
- Before applying statistical tests, we must make sure that the correct statistical approach is used. Therefore, each data set has to be tested for normality to find if the underlying distribution of the samples is normal. The simplest normality tests usually indicate if the distribution is normal or not, but do not show the type of the distribution. Also a test of data independence will be performed.The travel time, delay time, and distance data were collected simultaneously for all three methods, but we cannot evaluate normality for data obtained in series; therefore they will be evaluated in pairs: manual and DMI methods, DMI and GPS methods, and GPS and manual to compare and evaluate the behavior of the results.
3.1. Analysis for Normality
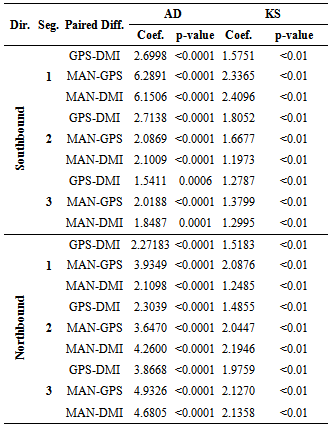
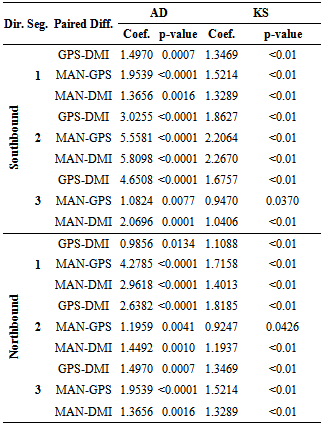
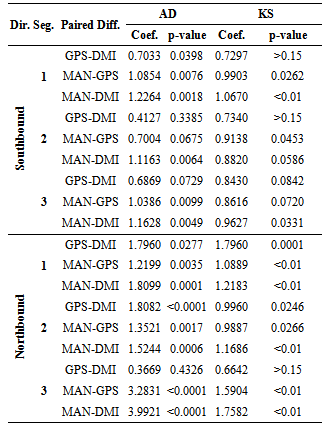
- The purpose of the normality tests is to see whether there is detectable evidence that the normality assumptions for a given hypothesis test are being violated. Each test has its own set of assumptions to be held. For instance, the paired t-test assumes that the differences of the samples are independent and normally distributed. Most of the normality tests do not indicate the cause of the non-normality, but only detect that the normality assumption has been violated. It is also known that small sample sizes usually are in agreement with the normality assumption, and therefore, it isharder to detect the assumption violation.There are several normality tests known, such as Lilliefor's, Kolmogorov-Smirnov (KS), Anderson-Darling (AD), andD'Agostino-Pearson. The most common goodness-of-fit test is the KS test, which helps determine if the sample population follows a specific distribution, and it is based on an empirical distribution function. The KS test hypothesis is defined as:Ho: the data comes from a specific distributionHA: the data does not follow a specific distributionThe more appropriate normality test is the AD test. It is a modification of the KS test and has several advantages over that, including the fact that it is more sensitive on tails. The analysis in this section involves only two tests for normality: the AD and KS tests, which both are based on a cumulative distribution function[15][16].Results of the normality tests are displayed in Table 2, Table 3, and Table 4. There we find that the majority of our data samples do not follow a normal distribution at the α = 0.05 level, either with the AD or KS test as indicated by a small p-value indicating that normal distribution is highly unlikely.
|
|
|
3.2. Analysis for Independence
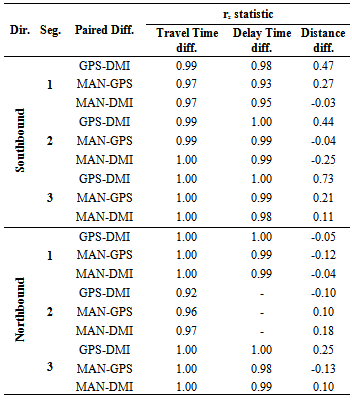
- The degree to which two variables are related to each other can be measured using the Pearson Product Moment Sample Correlation Coefficient[17][18]. However, previously we have determined that our data does not follow a normal distribution; therefore, we must use the Spearman test, which is used for non-normal data. This is a test of independence based on ranks, where rs is the correlation coefficient. The correlation value ranges between -1 to +1, where +1 indicates a perfect positive correlation between the n variables, but - 1 indicates a perfect negative relationship. There is no relationship between the variables if the correlation coefficient is zero or very close to zero. The correlation test has been applied to each data set.From the correlation results of the travel time and delay time data in Table 5, one can clearly see that the given continuous data are closely correlated, therefore, dependent. As a result, only non-parametric or distribution-free statistics can be applied for further data analysis. Although distance measurements in Table 5 indicate little correlation between the variables, showing either weak positive or negative relationship between the data sets, non-parametric tests will also be applied to distance data.
|
3.3. Non-parametric Statistical Tests
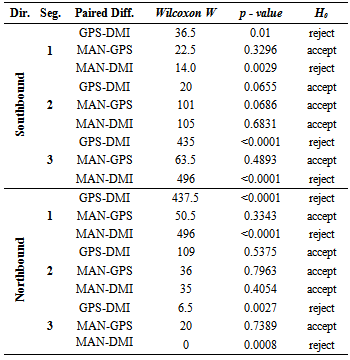
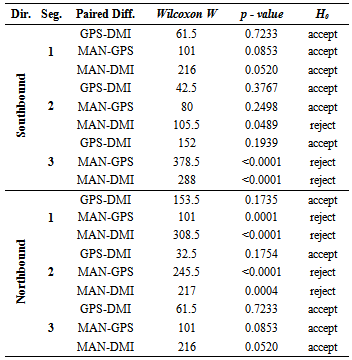
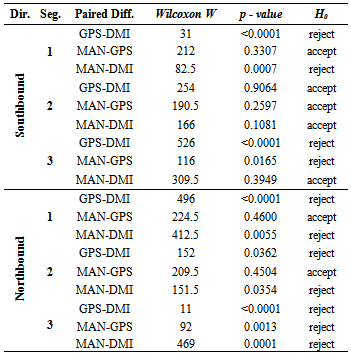
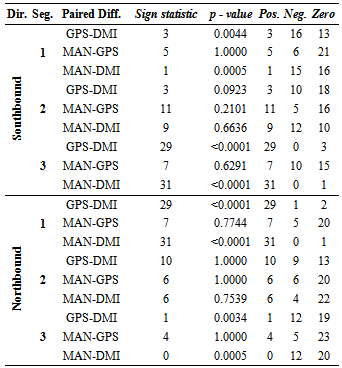
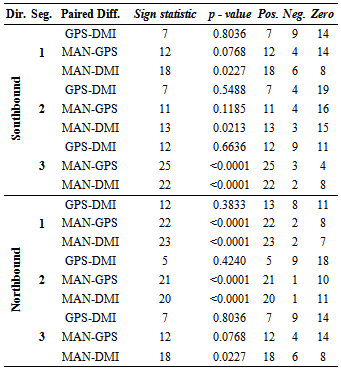
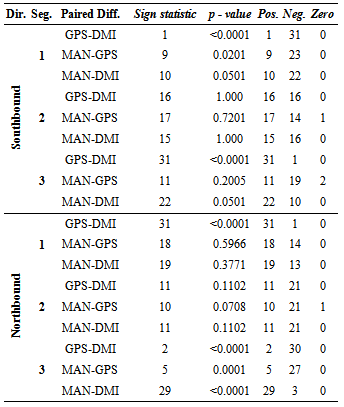
- Parametric statistics assume that a given population follows a normal distribution with a mean μ, and variance σ2. On the other hand, non-parametric statistics have no assumption about the underlying distribution; therefore, it is often called a distribution-free statistic[17][19]. In previous sections we determined that travel time, delay, and most of distance data are not normal and are dependent. Therefore, travel time data collection method paired data will be evaluated using the three non-parametric tests: Wilcoxon Signed Rank test, Sign test, and Minimum Chi-square test.Wilcoxon Signed Rank TestWilcoxon Signed Rank test is known as the nonparametric alternative to the paired t-test. The Wilcoxon Signed Rank Test is designed to test the hypothesis about a shift in location of a median Ө in the distribution. However, there are a few assumptions to be considered:■ the paired differences are assumed to be independent,■ each paired difference comes from a continuous distribution that issymmetric, and■ the paired differences have the same median.The null hypothesis assumes that there is a zero shift of each distribution for the differences. First, the observations of the study are taken in pairs, and then the differences between each pair are calculated. The next step includes rank Ri of the differences from the smallest to the biggest, ordered by absolute value |Z1|, ..., |Zn| and summing the positive values to obtain T+ [17].
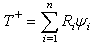 | (1) |
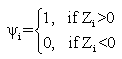 | (2) |
|
|
|
|
|
|
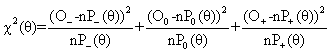 | (3) |
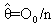 , the maximum likelihood estimator of θ, into χ2(θ), the minimum Chi-square statistic is equal to:
, the maximum likelihood estimator of θ, into χ2(θ), the minimum Chi-square statistic is equal to: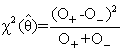 | (4) |
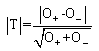 | (5) |
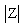 , where Z is a standard normal random variable. To solve Equation4,first the numbers of positive and negative values for each pair between the data methods are obtained. O+ is the number of positive signs and O- is the number of negative signs between the paired differences.An example of paired differences, that contains 23 zero values, is given below. We test Ho: P+ = P- and HA: P+≠ P-.An example is given for MAN-GPS travel time of northbound Segment 3:
, where Z is a standard normal random variable. To solve Equation4,first the numbers of positive and negative values for each pair between the data methods are obtained. O+ is the number of positive signs and O- is the number of negative signs between the paired differences.An example of paired differences, that contains 23 zero values, is given below. We test Ho: P+ = P- and HA: P+≠ P-.An example is given for MAN-GPS travel time of northbound Segment 3: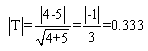 and
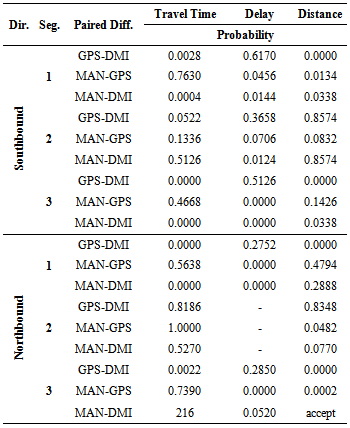
and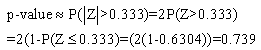 The results of the minimum Chi-square test are displayed in Table 12. According to the calculated values, manual and GPS methods for travel time measurements are not significantly different. In fact, the probability of them being equal is quite high. Comparing GPS and DMI methods and MAN-DMI methods, the results indicate that differences between the methods are not significant for Segment 2 only. For other segments, we reject the hypothesis that these data collection methods are equal. Differences between delay time measurements confirm that GPS and DMI methods are not significantly different when measuring delay times. However, comparisons between manual andGPS, as well as between manual and DMI, demonstrate that the pairs of these methods are not equal.
The results of the minimum Chi-square test are displayed in Table 12. According to the calculated values, manual and GPS methods for travel time measurements are not significantly different. In fact, the probability of them being equal is quite high. Comparing GPS and DMI methods and MAN-DMI methods, the results indicate that differences between the methods are not significant for Segment 2 only. For other segments, we reject the hypothesis that these data collection methods are equal. Differences between delay time measurements confirm that GPS and DMI methods are not significantly different when measuring delay times. However, comparisons between manual andGPS, as well as between manual and DMI, demonstrate that the pairs of these methods are not equal.
|
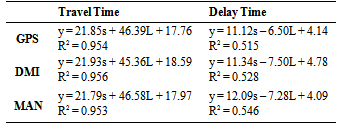
3.4. Additional Segment Analysis
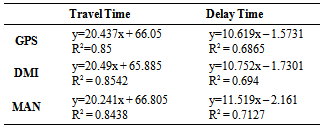
- The statistical analysis has shown that for certain roadway segments of the data collection the methods follow a pattern. It has been observed that Segment 2 in both directions has less difference between the methods.The tests possibly indicate that the methods vary according to the segment characteristics that have been described previously. The results might be a sign of correlation between the number of traffic lights on each segment and the impact on three data collection methods, as they become more apparent where segments with more traffic lights are present.Therefore, additional linear relationships measuring travel time and delay time per mile versus number of signals per mile have been created. Table 13 represents for each method, the linear regression of travel time and delay on the number of signals per mile. Results show that R2 values are fairly close to unity, which evidences the relationship between both the travel time and delay and the number of signals per mile. Moreover, a multiple regression analysis was conducted considering average travel time and average delay time as dependent values, and the average length of each segment and the number of lights per segment as independent values. L is the average length of segment in miles, and s represents the average number of lights per segment. Results are presented in Table 14.The result confirms that a relationship between the segment characteristics and travel time or delay time exists. However, one must be careful to draw conclusions, because the sample size of six is rather small to be sure about the results.
|
|
4. Conclusions and Recommendations
- The Wilcoxon Signed Rank Test, with a confidence level of 95%, has accepted Ho hypothesis for following number of data pairs:■ Travel time - 10 out of 18 data pairs■ Delay time - 8 out of 15 data pairs, and■ Distance - 7 out of 18 data pairs.On the other hand, the Sign test provides following results:■ Travel time - 10 out of 18 data pairs■ Delay time - 7 out of 15 data pairs, and■ Distance - 11 out of 18 data pairs.As a result, we conclude that at least a half of the data pairs rejects the Ho hypothesis and accepts HA hypothesis that the methods are not equal. The results show that the three travel data collection methods perform different for different data sets. We have reached a conclusion that manual and GPS methods perform equally well when collecting travel times on any of the segments. When conducting delay time studies, the GPS and DMI methods perform equally well. The manual method, assumingly, includes the difficulty of precisely reading the car's odometer, which is needed when estimating a speed of 5 mph and below.Distance measurements, using the three methods, indicate that manual-GPS and manual-DMI methods perform equally well. However, because we have rounded distance values for DMI to match the decimal places of odometer readings, we may get insufficient results to correctly conclude which method is performing better. The initial distance measurements collected by DMI represented rather close values in feet, sometimes ranging for only a couple of feet.On the other hand, the GPS collects the position data based on latitude and longitude, therefore a flat surface. Every great change in roadway grade introduces a small error in GPS distance measurements. Nevertheless, according to the statistical analysis, we would suggest the GPS method as the primary travel data collection method because we are interested in travel time and delay time consistent measurements.The comparison of the travel time data methods evaluated in this research, provided information about differences between the methods. It also indicated that the differences could be related to the road segment characteristics. However the sample size was not sufficient to make the final conclusions in this regard.An additional research could be conducted to investigate if the travel time method variations are based on road characteristics. This analysis could also be carried out comparing method performance during peak hour and compare with the off-peak hour performance. Also some odd results obtained could be attributed to rounding of the data and thus, it would be useful to perform more intensivedistance measurement comparison, and use the obtained values without data rounding.
ACKNOWLEDGEMENTS
- This work was partially supported by the Delaware Center for Transportation (DCT) co-sponsored by the University of Delaware and the Delaware Department of Transportation. The authors express their sincere gratitude to DCT for providing their extensive data sources.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML