Thomas Gabel1, Martin Riedmiller2
1Deutsche Flugsicherung GmbH, German Air Traffic Control, 61352, Langen, Germany
2Machine Learning Lab, Department of Computer Science, University of Freiburg, 79110, Freiburg, Germany
Correspondence to: Thomas Gabel, Deutsche Flugsicherung GmbH, German Air Traffic Control, 61352, Langen, Germany.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The optimization of traffic flow on roads and highways of modern industrialized countries is key to their economic growth and success. Besides, the reduction of traffic congestions and jams is also desirable from an ecological point of view as it yields a contribution to climate protection. In this article, we stick to a microscopic traffic simulation model and interpret the task of traffic flow optimization as a multi-agent learning problem. In so doing, we attach simple, adaptive agents to each of the vehicles and make them learn, using a distributed variant of model-free reinforcement learning, a cooperative driving behavior that is jointly optimal and aims at the prevention of traffic jams. Our approach is evaluated in a series of simulation experiments that emphasize that the substitution of selfish human behavior in traffic by the learned driving policies of the agents can result in substantial improvements in the quality of traffic flow.
Keywords:
Traffic Flow Control, Multi-Agent Systems, Reinforcement Learning, Microscopic Traffic Simulation
Cite this paper:
Thomas Gabel, Martin Riedmiller, "The Cooperative Driver: Multi-Agent Learning for Preventing Traffic Jams", International Journal of Traffic and Transportation Engineering, Vol. 1 No. 4, 2012, pp. 67-76. doi: 10.5923/j.ijtte.20120104.03.
1. Introduction
The amount of traffic has been growing continuously in the recent decades, and it is expected to increase even further in the future[1]. Since there is only limited space for new roads, a key factor to managing the growing volume of traffic is to use the existing infrastructure more efficiently. Meanwhile the computing power onboard individual vehicles has grown considerably recently and, therefore, is likely to facilitate an increased degree of autonomy in car control and, hence, a more efficient use of roads.Envisioning future car control systems, we might see the advent of vehicles that are controlled by fully autonomous agents such that the human can just lean back and enjoy the journey. In the scope of this work, we disregard the technical challenges of car control such as reliable vision and scene interpretation, track control, or the integration of sensing and acting (see[2] for a corresponding learning approach) and instead adopt a rather abstract, multi-agent point of view. While our focus is still on individual autonomous agents residing in the vehicles, we focus on these agents' goals of implementing a suitable high-level car control requiring the interaction with other traffic participants.We start by providing a review on contemporary methods for traffic flow simulation (Section 2). In so doing, we identify one microscopic traffic simulation model which is particularly suitable for our purposes as it reliably reproduces human behavior in traffic, including the sudden emergence of jams in dense traffic. Moreover, its microscopic character is beneficial, when intending to adopt a multi-agent perspective on traffic control. This is exactly what we do in Section 3. We attach simple, but adaptive agents to all vehicles involved in the simulation and make them learn a driving behavior that is jointly cooperative and aims at both, the prevention of traffic jams and the maximization of traffic flow. In order to achieve this the learning agents employ a distributed variant of model-free reinforcement learning. Moreover, we provide a formal grounding for our learning approach by embedding it into the framework of decentralized Markov decision processes. Finally, we devote Section 4 to an empirical evaluation that investigates to which extent the adaptive agents succeed in improving their driving behavior and the quality of traffic.
2. Traffic Flow Simulation
Modeling traffic flow is an active field of research. From an abstract point of view, existing traffic flow models can be classified with respect to the resolution of the dynamics they are modeling. On the one hand, macroscopic models are based on physical models and describe the traffic flow by equations for averaged quantities like vehicle density, average velocity, or traffic flow. By contrast, microscopic models address the problem by modeling individual vehicle dynamics. They describe the traffic flow based on the characteristics and behavior of single traffic units (driver and vehicle) and model, e.g., how individual vehicles follow one another or how lane changes are accomplished. There is also a third form of traffic models, mesoscopic models, where the individual behavior of a vehicle and driver, respectively, are described by mean field quantities, such as the mean vehicle density of a region in which a vehicle currently moves.In the article at hand, we advocate a multi-agent learning approach to traffic flow control. Accordingly, our focus is on microscopic traffic flow models because these correspond most naturally to a multi-agent view on traffic control. Therefore, we start by providing some basics about microscopic traffic flow models and about one particular instance of these models, before we present our learning approach.
2.1. Microscopic Car-Following
Microscopic traffic models describe the dynamics of individual vehicles as a function of the distances and velocities of neighboring vehicles. In this article, we consider single-lane traffic only, where the dynamics of interaction boil down to car-following. Extending our work towards more sophisticated models with multiple lanes and passing maneuvers are topics of future work.All car-following models start from the quite obvious observation that a change in velocity is only desired, if a vehicle's current velocity 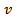 does not coincide with the corresponding driver's desired velocity
does not coincide with the corresponding driver's desired velocity 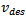 . The latter may be subject to physical limits, safety considerations, as well as legal regulations. Most of the classical car-following models can be traced back to the rather simple idea that a driver aims at reaching a desired velocity by using
. The latter may be subject to physical limits, safety considerations, as well as legal regulations. Most of the classical car-following models can be traced back to the rather simple idea that a driver aims at reaching a desired velocity by using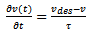 | (1) |
to modify the current velocity with strongly varying interpretations and values of 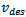 and
and 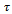 [3,4,5]. What is common to these classical models is that they determine vehicle velocities by solving differential equations. Another approach, called coupled map or cellular automata modeling, follows the idea to calculate vehicle velocities in discrete time steps, taking the situation in the preceding step into account to determine the velocities in the successor state[6,7]. This modeling approach features the advantage of being computationally efficient. Moreover, it is attractive from an agent-based perspective as it centers the focus on the individual vehicle or some kind of agent residing in it, enabling it to explicitly and autonomously act within the environment.The probably most important representative of this class of models is the Nagel-Schreckenberg model[8] which decomposes the road into segments of fixed length, allows each cell to be empty or occupied, and represents the velocity by an integer that indicates the number of cells a vehicle passes in a single time step. The model also incorporates stochasticity to account for imperfection in modeling driver behavior and, most importantly, very well simulates real traffic conditions including situations of traffic congestion.
[3,4,5]. What is common to these classical models is that they determine vehicle velocities by solving differential equations. Another approach, called coupled map or cellular automata modeling, follows the idea to calculate vehicle velocities in discrete time steps, taking the situation in the preceding step into account to determine the velocities in the successor state[6,7]. This modeling approach features the advantage of being computationally efficient. Moreover, it is attractive from an agent-based perspective as it centers the focus on the individual vehicle or some kind of agent residing in it, enabling it to explicitly and autonomously act within the environment.The probably most important representative of this class of models is the Nagel-Schreckenberg model[8] which decomposes the road into segments of fixed length, allows each cell to be empty or occupied, and represents the velocity by an integer that indicates the number of cells a vehicle passes in a single time step. The model also incorporates stochasticity to account for imperfection in modeling driver behavior and, most importantly, very well simulates real traffic conditions including situations of traffic congestion.
2.2. The Krauss Model
In what follows, we focus on an extension of the Nagel-Schreckenberg model which has been suggested[9] to reliably describe the behavior of humans in real traffic and, in particular, to describe jamming. This so-called Krauss model is a microscopic traffic flow model that is based on a small set of general and simple assumptions regarding traffic. Despite its simplicity it captures many properties of human behavior and real-world traffic clustering and jams. For example, it is capable of reflecting the fact that jams arise under “pure” conditions (i.e. not just due to obstacles) and that the transition from free flow to a jam occurs as a phase transition.The Krauss model utilizes a discrete time, but continuous space modeling of traffic. The basic assumption of the Krauss model is that there exist rather general properties of traffic flow which govern the behavior of the drivers. Thus, the macroscopic properties of traffic that can be observed are not pre-determined by the specific behavior of an individual traffic participant, but by general behavior patterns.Krauss distinguished between two different types of vehicle motion: free or interactionless motion and motion of a vehicle while interacting with another vehicle. Both of them are constrained by certain assumptions. The former one is restricted by the maximum speed of the vehicle, i.e. 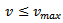 , while at the same time it is assumed that a driver desires to move as fast as possible. Thus, in free flow,
, while at the same time it is assumed that a driver desires to move as fast as possible. Thus, in free flow, 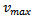 is the desired velocity
is the desired velocity 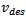 of a driver.Concerning motion while interacting with other vehicles, any driver's primary incentive is to avoid a collision with a preceding vehicle. To this end, Krauss makes the central assumption that any motion is free of collisions. As a consequence, drivers are constrained to always limit their velocity to a value
of a driver.Concerning motion while interacting with other vehicles, any driver's primary incentive is to avoid a collision with a preceding vehicle. To this end, Krauss makes the central assumption that any motion is free of collisions. As a consequence, drivers are constrained to always limit their velocity to a value 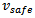 that guarantees breaking to a full stop while not colliding with the preceding vehicle, i.e. it always holds
that guarantees breaking to a full stop while not colliding with the preceding vehicle, i.e. it always holds 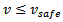 . The determination of
. The determination of 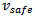 contains all the information about how vehicles interact with one another.A final assumption the Krauss model makes concerns the physical properties of the vehicles. The values of the maximal acceleration
contains all the information about how vehicles interact with one another.A final assumption the Krauss model makes concerns the physical properties of the vehicles. The values of the maximal acceleration 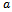 and the breaking acceleration
and the breaking acceleration 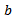 of vehicles are bounded, i.e.
of vehicles are bounded, i.e. 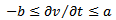 with
with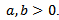 Traffic simulation in the Krauss model takes place in discrete time steps
Traffic simulation in the Krauss model takes place in discrete time steps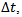 while space variables are continuous. This gives rise to the following inequation that holds true for the velocity of each vehicle:
while space variables are continuous. This gives rise to the following inequation that holds true for the velocity of each vehicle: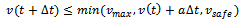 | (2) |
where 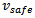 is determined with respect to the maximum breaking constraint
is determined with respect to the maximum breaking constraint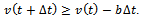 | (3) |
Given these ingredients, Krauss formulates his traffic flow model as follows: In each time step, every driver selects the highest velocity that is compatible with the constraints and limits mentioned so far. This boils down to the following four update rules that are to be applied for every vehicle in every time step:• Safety Considerations (collision-free movements):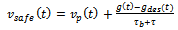 | (4) |
• Desired Velocity (fastest possible movement):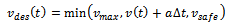 | (5) |
• Random Perturbation (lingering):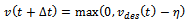 | (6) |
• Actual Movement in Space: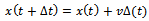 | (7) |
Furthermore, 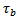 denotes the time required to come to a full stop which Krauss approximates by
denotes the time required to come to a full stop which Krauss approximates by 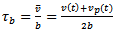 | (8) |
Accordingly, the concrete formula for the safe velocity takes the form 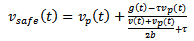 | (9) |
Finally, the Krauss model follows the Gipps family[6] of traffic flow models by assuming that a time step 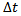 is equal to the reaction time
is equal to the reaction time 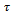 with a typical setting of
with a typical setting of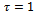 . Therefore, the length of a vehicle is not its true physical length, but the space that it covers in a dense jam, i.e. a slightly larger quantity. Putting these settings together, the formula for
. Therefore, the length of a vehicle is not its true physical length, but the space that it covers in a dense jam, i.e. a slightly larger quantity. Putting these settings together, the formula for 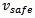 becomes
becomes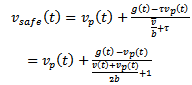 | (10) |
Equation 6 models the human factor in driving. It reflects the fact that during car-following individual drivers may linger, i.e. they deviate from the desire of driving at a maximal or safe velocity in a random manner, for example because they are distracted or too cautious. In this perturbation step, each car is slowed down by a random amount 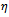 which is uniformly distributed over the interval
which is uniformly distributed over the interval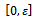 , where
, where 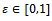 is the noise parameter of the model.
is the noise parameter of the model.
2.3. The Occurrence of Jams
The Krauss model is based on a set of four update equations and has four free parameters: the maximal velocity (though maximal velocity has a clear macroscopic meaning and is, thus, typically not considered a “free” parameter), 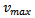 , the maximal acceleration
, the maximal acceleration 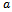 , the maximal deceleration
, the maximal deceleration 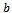 , and the noise (or lingering) parameter
, and the noise (or lingering) parameter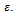 The relation of the exact values of
The relation of the exact values of 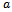 and
and 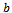 plays a crucial role as to whether a traffic flow simulation based on the Krauss model exhibits realistic properties, i.e. whether it successfully models real traffic, or not. To this end, three fundamentally different cases are distinguished[9] which result in qualitatively different types of behavior: • the high acceleration limit with
plays a crucial role as to whether a traffic flow simulation based on the Krauss model exhibits realistic properties, i.e. whether it successfully models real traffic, or not. To this end, three fundamentally different cases are distinguished[9] which result in qualitatively different types of behavior: • the high acceleration limit with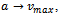 • the high deceleration limit with
• the high deceleration limit with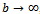 , and • the low acceleration, low deceleration setting with
, and • the low acceleration, low deceleration setting with 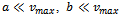 . However, only model instances of the third type exhibit macroscopically realistic behavior and, hence, describe real traffic in a qualitatively accurate way. For example, only in this setting jams feature a stable outflow and they arise “out of nothing”, i.e. the phase transition-like occurrence of jams is present. In essence, the Krauss model is capable of simulating real-world traffic well, if the acceleration and deceleration are limited to values that correspond to realistic vehicle dynamics. Clearly, we stick to such a setting in the remainder of this article.In order to realize a realistic model of jamming two basic ingredients must be given[9]. On the one hand, vehicles must be able to slow down to a velocity slower than that of the leading car. On the other hand, the outflow from traffic congestions must be lower than the maximum flow. In the traffic flow model under consideration both of these characteristics are implemented by the noise term (cf.
. However, only model instances of the third type exhibit macroscopically realistic behavior and, hence, describe real traffic in a qualitatively accurate way. For example, only in this setting jams feature a stable outflow and they arise “out of nothing”, i.e. the phase transition-like occurrence of jams is present. In essence, the Krauss model is capable of simulating real-world traffic well, if the acceleration and deceleration are limited to values that correspond to realistic vehicle dynamics. Clearly, we stick to such a setting in the remainder of this article.In order to realize a realistic model of jamming two basic ingredients must be given[9]. On the one hand, vehicles must be able to slow down to a velocity slower than that of the leading car. On the other hand, the outflow from traffic congestions must be lower than the maximum flow. In the traffic flow model under consideration both of these characteristics are implemented by the noise term (cf. 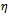 in Equation (6)) which is subject to the noise parameter
in Equation (6)) which is subject to the noise parameter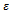 .Let us consider the first of these two features in more detail. The noise term implements overreactions that destabilize dense traffic. Drivers slow down their velocity to a value lower than necessary. This can lead to the emergence of a jam, where the probability for this to happen increases with the density of the traffic. Krauss points out that for any value of the noise parameter there is a value of the traffic's density, where the traffic typically breaks down due to the drivers' overreactions modeled by
.Let us consider the first of these two features in more detail. The noise term implements overreactions that destabilize dense traffic. Drivers slow down their velocity to a value lower than necessary. This can lead to the emergence of a jam, where the probability for this to happen increases with the density of the traffic. Krauss points out that for any value of the noise parameter there is a value of the traffic's density, where the traffic typically breaks down due to the drivers' overreactions modeled by 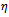 . This breakdown comes along with a reduction of the average flow of traffic – which is the average number of vehicles passing a fixed section within a given time interval – and can be characterized by the difference of the homogeneous flow and the flow in a jammed state. While this difference vanishes for small noise values, it grows to a substantial amount as
. This breakdown comes along with a reduction of the average flow of traffic – which is the average number of vehicles passing a fixed section within a given time interval – and can be characterized by the difference of the homogeneous flow and the flow in a jammed state. While this difference vanishes for small noise values, it grows to a substantial amount as 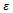 becomes larger than 0.5. In other words, for a fixed traffic density and small values of
becomes larger than 0.5. In other words, for a fixed traffic density and small values of 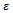 (and, in particular, for the noise-free setting
(and, in particular, for the noise-free setting 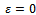 ) the entire traffic flow is deterministic and the model degenerates to a simulation that remains unchangeably in a state of constant flow. Consequently, to allow for a meaningful simulation and to allow for a realistic occurrence and analysis of jams, the noise parameter must be set to reasonably large values.
) the entire traffic flow is deterministic and the model degenerates to a simulation that remains unchangeably in a state of constant flow. Consequently, to allow for a meaningful simulation and to allow for a realistic occurrence and analysis of jams, the noise parameter must be set to reasonably large values.
2.4. Motivation for a Multi-Agent Approach
So far, we have summarized the foundations of the Krauss model. This microscopic traffic flow model is able to accomplish a realistic traffic simulation, including traffic congestions, as it appropriately models how humans behave in real-world traffic. In essence, humans aim at moving as fast as possible, but also tend to linger from time to time.In the following, we suggest to replace the human drivers in this microscopic simulation by intelligent autonomous agents that are capable of learning to behave in a cooperative manner. By cooperative we mean a behavior that reduces the costs for the entire set of traffic participants, where the interpretation of costs may take different forms. For example, it may be desired to maximize the average velocity of all vehicles, to limit or ban the occurrence of jams, or to reduce the joint emission of fumes. These optimization goals are, in general, not achieved with human drivers due to the selfish behavior of humans captured in the Krauss model. To the best of the authors' knowledge this approach is novel.A microscopic traffic flow model like the Krauss model represents a good starting point for our research for two main reasons. First, the concept of individually acting agents can be easily implemented due to the microscopic character of the model. Second, Krauss-based simulations model very well human and real-world traffic. As a consequence, we might expect that a machine learning approach using a massive set of independently learning agents might overcome certain limitations and disadvantages of the macroscopic traffic patterns that are arising due to suboptimal human behavior in traffic. In order to allow for a fair comparison, it is also our goal to facilitate the application of an agent's learned behavior without extensive requirements regarding inter-vehicle communication. This means the car controlling agents must base their decisions on the same amount of information as human drivers do.
3. Traffic Simulation as Decentralized MDP
We have pointed out that selfish and not farsighted human behavior can yield severe disturbances to dense traffic. In what follows, we propose a multi-agent reinforcement learning approach in which we attach a single learning agent to each vehicle and aim at making the collective of all agents learn a behavior that is jointly cooperative and superior to human car control in the Krauss model.
3.1. Foundations
For a formal characterization of the learning problem, we embed the problem settings of our interest into the framework of decentralized Markov decision processes (DEC-MDP) by Bernstein et al.[10].Definition 1. A factored 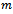 -agent DEC-MDP
-agent DEC-MDP 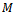 is defined by a tuple
is defined by a tuple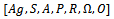 with•
with• 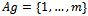 as the set of agents,•
as the set of agents,• 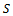 as the set of world states which can be factored into
as the set of world states which can be factored into 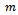 components
components 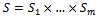 (the
(the 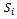 belong to one of the agents each)• and
belong to one of the agents each)• and 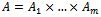 as the set of joint actions to be performed by the agents (
as the set of joint actions to be performed by the agents ( denotes a joint action that is made up of elementary actions
denotes a joint action that is made up of elementary actions 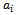 taken by agent
taken by agent 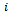 ).•
).• 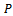 is the transition function with
is the transition function with 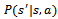 denoting the probability that the system arrives at state
denoting the probability that the system arrives at state 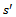 upon executing
upon executing 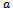 in
in 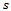 and•
and• 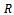 is the reward function with
is the reward function with 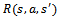 denoting the reward for executing
denoting the reward for executing 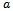 in
in 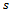 and transitioning to
and transitioning to 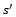 .•
.• 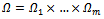 represents the set of all observations of all agents (
represents the set of all observations of all agents ( denotes a joint observation with
denotes a joint observation with 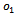 as the observation for agent
as the observation for agent 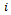 ) and•
) and• 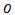 is the observation function that determines the probability
is the observation function that determines the probability 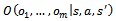 that agent 1 through
that agent 1 through 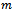 perceive observations
perceive observations 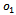 through
through 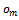 upon the execution of
upon the execution of 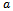 in
in 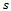 and entering
and entering 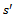 .•
.• 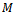 s jointly fully observable, i.e. the current state is fully determined by the amalgamation of all agents' observations:
s jointly fully observable, i.e. the current state is fully determined by the amalgamation of all agents' observations: 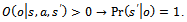 To the agent-specific components,
To the agent-specific components, 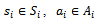 ,
, 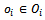 we refer as local state, local action, and local observation of agent
we refer as local state, local action, and local observation of agent 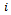 , respectively.A joint policy
, respectively.A joint policy 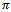 is a set of local policies
is a set of local policies 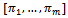 each of which is, in the general case, a mapping from agent
each of which is, in the general case, a mapping from agent 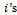 sequence of local observations to local actions, i.e.
sequence of local observations to local actions, i.e. 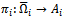 . In a memoryless, reactive setting, local policies are defined over the most recent observation only, i.e.
. In a memoryless, reactive setting, local policies are defined over the most recent observation only, i.e. 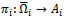 .A practically relevant case, however, is when each agent can fully observe its local state.Definition 2. A factored
.A practically relevant case, however, is when each agent can fully observe its local state.Definition 2. A factored 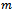 -agent DEC-MDP has local full observability, if for all agents
-agent DEC-MDP has local full observability, if for all agents 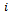 and for all local observations
and for all local observations 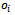 there is a local state
there is a local state 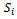 such that
such that 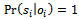 .It is important to note that joint full observability together with local full observability of a decentralized MDP do generally not imply full observability. Instead, vast parts of the global state are hidden from each of the agents[11].We also need to characterize the problems of our interest with respect to the inter-agent dependencies in their reward, transition, and observation functions. A factored
.It is important to note that joint full observability together with local full observability of a decentralized MDP do generally not imply full observability. Instead, vast parts of the global state are hidden from each of the agents[11].We also need to characterize the problems of our interest with respect to the inter-agent dependencies in their reward, transition, and observation functions. A factored 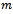 -agent DEC-MDP is called reward independent, if there exist local functions
-agent DEC-MDP is called reward independent, if there exist local functions 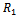 through
through 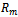 , each depending on local states and actions of the agents only, as well as a function
, each depending on local states and actions of the agents only, as well as a function 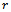 that amalgamates the global reward value from the local ones, such that maximizing each
that amalgamates the global reward value from the local ones, such that maximizing each 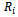 individually also yields a maximization of
individually also yields a maximization of 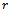 .If, in a factored
.If, in a factored 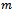 -agent DEC-MDP, the observation each agent sees depends only on its current and next local state and on its action, then the corresponding DEC-MDP is called observation independent, i.e.
-agent DEC-MDP, the observation each agent sees depends only on its current and next local state and on its action, then the corresponding DEC-MDP is called observation independent, i.e.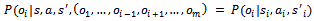 . Then, in combination with local full observability, the observation-related components
. Then, in combination with local full observability, the observation-related components 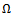 and
and 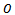 are redundant and can be removed from Definition 2.The DEC-MDPs we consider subsequently are observation and reward independent, but they are not transition independent. Hence, the state transition probabilities of one agent are in general also influenced by other agents. However, in what follows, we assume that there are certain regularities in the dependencies between the agents. In particular, the local action of agent
are redundant and can be removed from Definition 2.The DEC-MDPs we consider subsequently are observation and reward independent, but they are not transition independent. Hence, the state transition probabilities of one agent are in general also influenced by other agents. However, in what follows, we assume that there are certain regularities in the dependencies between the agents. In particular, the local action of agent 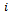 affects its own local state as well as the local state of exactly one other (always the same) agent
affects its own local state as well as the local state of exactly one other (always the same) agent 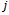 . This gives rise to the following definition.Definition 3. A factored
. This gives rise to the following definition.Definition 3. A factored 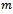 -agent DEC-MDP has circular transition dependencies, if the local state of agent
-agent DEC-MDP has circular transition dependencies, if the local state of agent 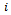 is influenced by the local action of itself as well as by the local action of agent
is influenced by the local action of itself as well as by the local action of agent 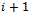 for all
for all 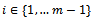 and by the local action of agent
and by the local action of agent 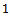 for
for 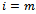 .
.
3.2. Problem Modeling
Obviously, this definition has been chosen in regard to the traffic simulation in the Krauss model where binary interactions between vehicles are captured. To be exact, traffic flow optimization problems can be modelled using factored 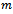 -agent DEC-MDPs with circular dependencies because:• The state of the road, i.e. the global world state is factored where each vehicle observes only a small fraction of it. We attach to each vehicle an agent
-agent DEC-MDPs with circular dependencies because:• The state of the road, i.e. the global world state is factored where each vehicle observes only a small fraction of it. We attach to each vehicle an agent 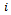 whose local state can be described by the observations that individual vehicles get hold of in the Krauss model.• State transitions are non-deterministic for a noise level
whose local state can be described by the observations that individual vehicles get hold of in the Krauss model.• State transitions are non-deterministic for a noise level 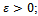 the system model is not known by the agents.• The local state
the system model is not known by the agents.• The local state 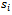 is fully described by its velocity, the velocity of its preceding vehicle as well as the gap between the two. These are the variables necessary in the Krauss model to calculate the current value of the safe velocity
is fully described by its velocity, the velocity of its preceding vehicle as well as the gap between the two. These are the variables necessary in the Krauss model to calculate the current value of the safe velocity 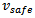 (cf. Equation 10). The combination of all local states fully identifies the global system state, i.e. the problem is a DEC-MDP, and not a DEC-POMDP.The local state space of each agent
(cf. Equation 10). The combination of all local states fully identifies the global system state, i.e. the problem is a DEC-MDP, and not a DEC-POMDP.The local state space of each agent 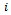 is a real-valued three-dimensional vector, i.e.
is a real-valued three-dimensional vector, i.e. 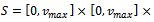
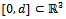 with
with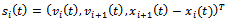 | (11) |
• Interactions between agents are strongly limited. The local state of any vehicle can be affected only by its own actions and by the actions of the directly preceding vehicle. This is reflected by the constraint of circular transition dependencies 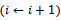 specified in Definition 3.• Given a fixed traffic density
specified in Definition 3.• Given a fixed traffic density 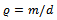 (with
(with 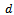 denoting the length of the track considered and
denoting the length of the track considered and 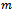 the number of vehicles), the traffic flow is defined as
the number of vehicles), the traffic flow is defined as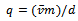 with
with 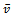 indicating the average velocity of all vehicles. Rewriting this equation, we see that it holds
indicating the average velocity of all vehicles. Rewriting this equation, we see that it holds 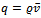 , which hints to the fact that the global traffic flow is proportional to the average velocity
, which hints to the fact that the global traffic flow is proportional to the average velocity 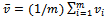 of the vehicles, given a fixed traffic density, i.e. a constant number of
of the vehicles, given a fixed traffic density, i.e. a constant number of 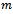 vehicles on the track. As a consequence, the corresponding DEC-MDP can be constructed to be reward-independent, if we associate the differences between the velocities of individual vehicles in their next and current time step with the local reward functions
vehicles on the track. As a consequence, the corresponding DEC-MDP can be constructed to be reward-independent, if we associate the differences between the velocities of individual vehicles in their next and current time step with the local reward functions 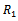 through
through 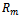 , i.e.
, i.e. 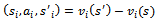 and use
and use 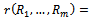
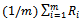 as amalgamation function (cf. Definition 1).All vehicles are independent of one another. They do not communicate with one another and choose their driving behavior independently. In the Krauss model each driver increments selfishly the desired velocity
as amalgamation function (cf. Definition 1).All vehicles are independent of one another. They do not communicate with one another and choose their driving behavior independently. In the Krauss model each driver increments selfishly the desired velocity 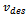 , until
, until 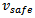 or
or 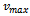 are reached. In order to allow for cooperative behavior, each agent must be enabled to willingly decide to not increase its current velocity as much as it possibly could, considering the current traffic situation.To this end, we facilitate each agent with the degree of freedom to select its desired velocity
are reached. In order to allow for cooperative behavior, each agent must be enabled to willingly decide to not increase its current velocity as much as it possibly could, considering the current traffic situation.To this end, we facilitate each agent with the degree of freedom to select its desired velocity 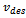 according to
according to 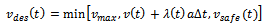 | (12) |
Here, the value of 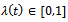 determines the share of the acceleration capabilities that the agent uses in the current time step. Thus, the choice for a concrete value of
determines the share of the acceleration capabilities that the agent uses in the current time step. Thus, the choice for a concrete value of 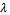 must be done in each time step and, accordingly, corresponds to the current action of the agent considered. Based on this we define the agents' local policies as follows.Definition 4. Given a factored
must be done in each time step and, accordingly, corresponds to the current action of the agent considered. Based on this we define the agents' local policies as follows.Definition 4. Given a factored 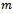 -agent DEC-MDP with circular transition dependencies, a local reactive policy of agent
-agent DEC-MDP with circular transition dependencies, a local reactive policy of agent 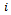 is defined as a mapping
is defined as a mapping 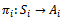 where
where 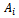 is a finite subset of
is a finite subset of 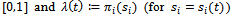 is used in update Equation 12.In the remainder of this article, we set
is used in update Equation 12.In the remainder of this article, we set 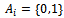 for all
for all 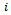 , which means that at any time step each agent can choose between a full acceleration as determined by Equation 5 and a steady motion, i.e. not to alter its current velocity. Note, however, that the velocity of an agent is still subject to the noise term (cf. Equation 7) and may, thus, be decreased randomly. More fine-grained or even continuous action sets might be employed, too, and would allow for an even higher degree of velocity control by the agent. This is subject of future work.
, which means that at any time step each agent can choose between a full acceleration as determined by Equation 5 and a steady motion, i.e. not to alter its current velocity. Note, however, that the velocity of an agent is still subject to the noise term (cf. Equation 7) and may, thus, be decreased randomly. More fine-grained or even continuous action sets might be employed, too, and would allow for an even higher degree of velocity control by the agent. This is subject of future work.
3.3. Massive Multi-Agent Learning
Solving a DEC-MDP optimally is NEXP-hard and thus intractable for all except the smallest problem sizes[12]. However, it is not our goal to find the optimal joint policy, but to come up with a policy of high quality in reasonable time. Speaking about the quality of a policy, the term quality translates to a policy that yields high traffic flow while avoiding traffic jams. We let the agents acquire their local policies jointly with the other agents by repeated interaction with the DEC-MDP and concurrent evolvement of the policies. Since the state transition and reward model of the problem are not known to the agents we employ model-free reinforcement learning[13].The agents use the well-known Q learning algorithm to update a local value function 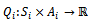 according to
according to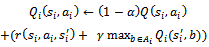 | (13) |
after having experienced a single local state transition 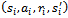 [14]. The learning rate is denoted by
[14]. The learning rate is denoted by  , the discount factor by
, the discount factor by 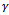 . For the case of finite state and action spaces where the Q function can be represented using a look-up table, there are convergence guarantees that say Q learning converges to the optimal state-action value function with probability one, assuming that all state-action pairs are visited infinitely often and that the learning rate
. For the case of finite state and action spaces where the Q function can be represented using a look-up table, there are convergence guarantees that say Q learning converges to the optimal state-action value function with probability one, assuming that all state-action pairs are visited infinitely often and that the learning rate  diminishes appropriately. From a given state-action value function
diminishes appropriately. From a given state-action value function 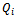 a greedy policy can be derived according to
a greedy policy can be derived according to 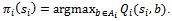 | (14) |
As the state space 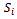 to be considered by the agents is continuous, we employ a straightforward regular grid in order to discretize
to be considered by the agents is continuous, we employ a straightforward regular grid in order to discretize 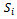 . To this end, we decompose the first state variable (relating to the vehicle's velocity) into 41 different values, the second one (preceding vehicle's velocity) into 21 values, and the third one (the gap between the two) into 21 values, giving rise to an abstract state space made up of
. To this end, we decompose the first state variable (relating to the vehicle's velocity) into 41 different values, the second one (preceding vehicle's velocity) into 21 values, and the third one (the gap between the two) into 21 values, giving rise to an abstract state space made up of 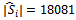 abstract states.For the time being, we grant all agents access to the same
abstract states.For the time being, we grant all agents access to the same 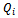 table, i.e. to the same data structure. This approach allows for a tremendous speed-up of the learning process as the experience tuples and belonging Q updates according to Equation 13 work on the same function
table, i.e. to the same data structure. This approach allows for a tremendous speed-up of the learning process as the experience tuples and belonging Q updates according to Equation 13 work on the same function  . Note that this, in principle, could enable the agents to get access to the other agents'
. Note that this, in principle, could enable the agents to get access to the other agents' 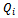 (because
(because 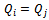 for all
for all 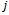 ) function and, thus, to their local policies
) function and, thus, to their local policies 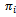 . However, this knowledge is not exploited during the learning process at all, i.e. our learning agents do not use
. However, this knowledge is not exploited during the learning process at all, i.e. our learning agents do not use 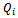 to draw conclusions regarding the other vehicles' behavior. In other words, we utilize a shared local state-action value function
to draw conclusions regarding the other vehicles' behavior. In other words, we utilize a shared local state-action value function 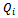 only for reasons of computational efficiency.In this regard, one might object that the coupling of all agents' local state-action value functions contradicts the idea of entirely independent and decoupled learners. Nevertheless, this approach is meaningful and of high practical relevance for several reasons: First, the agents still must act under extreme restrictions with respect to the global system state – they know only about the local traffic situation
only for reasons of computational efficiency.In this regard, one might object that the coupling of all agents' local state-action value functions contradicts the idea of entirely independent and decoupled learners. Nevertheless, this approach is meaningful and of high practical relevance for several reasons: First, the agents still must act under extreme restrictions with respect to the global system state – they know only about the local traffic situation 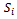 at their current location and they know nothing about the local state of other agents. Second, they do not know which actions were taken by the other agents (in fact, we disallow the agents to draw corresponding conclusions), and, as a matter of fact, even if they knew, this would be of little use because they are clueless about the local states other agents are in. Third, when thinking about a real-world implementation of a reinforcement learning approach for traffic flow optimization, it is standing to reason that the participating vehicles collect and transmit their transition data to a centralized entity (e.g. the manufacturer of certain vehicles or even a public traffic control institution), which distributes learned (and fixed)
at their current location and they know nothing about the local state of other agents. Second, they do not know which actions were taken by the other agents (in fact, we disallow the agents to draw corresponding conclusions), and, as a matter of fact, even if they knew, this would be of little use because they are clueless about the local states other agents are in. Third, when thinking about a real-world implementation of a reinforcement learning approach for traffic flow optimization, it is standing to reason that the participating vehicles collect and transmit their transition data to a centralized entity (e.g. the manufacturer of certain vehicles or even a public traffic control institution), which distributes learned (and fixed) 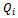 functions to all agents and lets the agents derive their local policies from this local state-action value function independently.
functions to all agents and lets the agents derive their local policies from this local state-action value function independently.
4. Empirical Evaluation
We start our investigations by examining under which circumstances the Krauss model yields a realistic simulation of human behavior and, thus, results in the emergence of jams out of nowhere in dense traffic. After having analyzed the specific conditions of the simulation model, we apply and evaluate the learning approach presented in the preceding chapter.
4.1. The Occurrence of Jams Revisited
We use a circular track of 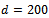 units in length that is populated with
units in length that is populated with 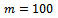 vehicles, where we start the simulation with all vehicles distributed equidistantly over the track with no initial velocity. Thus, for all
vehicles, where we start the simulation with all vehicles distributed equidistantly over the track with no initial velocity. Thus, for all 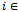
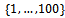 we have a gap
we have a gap 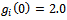 and initial velocities
and initial velocities 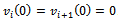 . Furthermore, we employ the settings of the acceleration and deceleration that Krauss identified to belong to the class of the “low acceleration, low deceleration” limit simulations
. Furthermore, we employ the settings of the acceleration and deceleration that Krauss identified to belong to the class of the “low acceleration, low deceleration” limit simulations 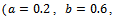
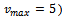 which, in general, yield the most realistic simulation.For ease of notion, we subsequently refer to the average velocity
which, in general, yield the most realistic simulation.For ease of notion, we subsequently refer to the average velocity 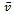 of all vehicles, when speaking about traffic flow
of all vehicles, when speaking about traffic flow 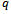 , because these two variables are proportional to one another (
, because these two variables are proportional to one another (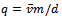 ). Speaking about realistic traffic, however, we have to clearly define what we consider to be a jamming state. Homogeneous flow – being the opposite of a jam – is characterized by all vehicles moving at constant speed under equidistant distribution over the track with a gap
). Speaking about realistic traffic, however, we have to clearly define what we consider to be a jamming state. Homogeneous flow – being the opposite of a jam – is characterized by all vehicles moving at constant speed under equidistant distribution over the track with a gap 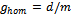 . Clearly, this state (for which it holds
. Clearly, this state (for which it holds 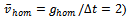 can only be attained in a noise free setting. In the remainder of this article, we say that a jam is present on the track, if• the traffic congestion results in a substantial reduction of the velocity of the cars involved, i.e. their velocity is below
can only be attained in a noise free setting. In the remainder of this article, we say that a jam is present on the track, if• the traffic congestion results in a substantial reduction of the velocity of the cars involved, i.e. their velocity is below  • the traffic congestion results in a crowding of vehicles, i.e. the gaps between the vehicles involved is below
• the traffic congestion results in a crowding of vehicles, i.e. the gaps between the vehicles involved is below 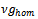 (we set
(we set 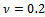 ), and• the traffic congestion is large enough, i.e. concerns at least
), and• the traffic congestion is large enough, i.e. concerns at least 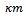 vehicles (we set
vehicles (we set 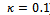 ).In Figure 1 we analyze the impact of the single remaining free parameter of the Krauss model (cf. Section 3.2), the noise or lingering parameter
).In Figure 1 we analyze the impact of the single remaining free parameter of the Krauss model (cf. Section 3.2), the noise or lingering parameter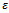 . The top chart shows for which noise levels jams emerge at all. Obviously for values of
. The top chart shows for which noise levels jams emerge at all. Obviously for values of 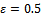 and below, traffic remains in a state of nearly homogeneous flow and the jamming conditions never occur (tested for
and below, traffic remains in a state of nearly homogeneous flow and the jamming conditions never occur (tested for 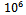 simulation steps). If we start the simulation for increasing values of
simulation steps). If we start the simulation for increasing values of 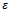 , however, the jamming state arises more and more quickly, for instance, on average after
, however, the jamming state arises more and more quickly, for instance, on average after 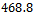 simulation steps for
simulation steps for 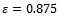 , if we start the simulation from the mentioned equidistant distribution of vehicles.The bottom part of Figure 1 visualizes to which average velocity the system converges in the long run. Apparently, for increasing noise values the flow of traffic is decreasing. It is important to note that for
, if we start the simulation from the mentioned equidistant distribution of vehicles.The bottom part of Figure 1 visualizes to which average velocity the system converges in the long run. Apparently, for increasing noise values the flow of traffic is decreasing. It is important to note that for 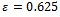 and above the equilibrium state, whose average velocity is plotted, contains a traffic jam (as indicated by the top chart).
and above the equilibrium state, whose average velocity is plotted, contains a traffic jam (as indicated by the top chart).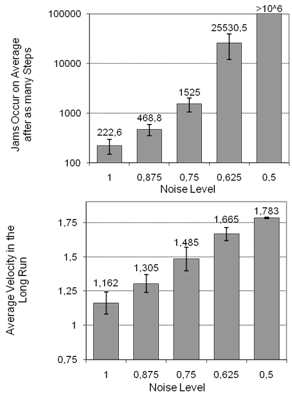 | Figure 1. Krauss-based traffic simulation for the scenario described in the text: Jam emergence and average vehicle velocity subject to varying noise levels |
Figure 2a) visualizes the development of the situation on the track for a noise value of 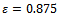 . While, initially, traffic is running smoothly, at some point of time small disturbances start to grow into significant congestions with a drop in average traffic flow. In this figure, a row of pixels shows the distribution of vehicles across the track for one instant of time (they move from left to right). With time steps increasing from top to bottom, this type of visualization captures the development of traffic flow over time. Specifically, this plot visualizes the first 700 simulation steps. Note that the varying colors of the individual vehicles are used for the purpose of better presentation only. Part b) of this figure shows the saturation state of the same scenario reached after 2000 time steps: Obviously, the system has gone into an equilibrium state with one big traffic jam and an average vehicle velocity of only
. While, initially, traffic is running smoothly, at some point of time small disturbances start to grow into significant congestions with a drop in average traffic flow. In this figure, a row of pixels shows the distribution of vehicles across the track for one instant of time (they move from left to right). With time steps increasing from top to bottom, this type of visualization captures the development of traffic flow over time. Specifically, this plot visualizes the first 700 simulation steps. Note that the varying colors of the individual vehicles are used for the purpose of better presentation only. Part b) of this figure shows the saturation state of the same scenario reached after 2000 time steps: Obviously, the system has gone into an equilibrium state with one big traffic jam and an average vehicle velocity of only 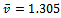 .
.
4.2. Learning Experiments
So far, we have focused on the actual conditions present in traffic simulations following the Krauss model. Next, we pursue the approach proposed in Section 4 and equip all vehicles with a learning agent. As pointed out, the agents' goal is to move quickly, where the reinforcement learning approach ought to make them develop an incentive to avoid jammings since the velocity of any vehicle in a jamming state is low. Consequently, we are interested in both the average velocity the agents yield when testing their learned policies as well as in the question whether they successfully avoid traffic congestions. In so doing, we target the following primary learning goals. | Figure 2. Starting from the initial state with equidistantly distributed vehicles, the selfish driving behavior under the Krauss update equations soon leads to minor congestions (a). After 2000 simulation steps a steady jam has emerged (b). Part (c) provides a snapshot taken during learning. The vehicles are reset to the starting state, after their inexperience has brought them into a jamming state. When the finally learned state-action value function is exploited greedily by the agents (shown in (d)), a homogeneous flow of high average velocity arises. The noise level in all parts is 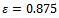 |
• As depicted in Figure 1, the human driving behavior captured in the Krauss model leads to the emergence of severe traffic jams. Avoiding this by the use of intelligent agents controlling the vehicles is our first goal.• No jam ever emerges under the “trivial” policy where the traffic participants move not at all or at very little speed. Of course, this is not a reasonable approach, which is why our second goal is to make the agents learn to move at least as quickly as in the Krauss model, while also striving for the first goal, i.e. preventing jams. • Our third concern regards the amount of fuel consumed by the learning agents which, of course, ought to be minimized.We start by focussing on the problem setting with 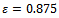 . The agents use a discount factor of
. The agents use a discount factor of 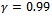 and, in order to account for the non-Markovian environment due to the changes in the policies of the other agents, a non-decaying learning rate
and, in order to account for the non-Markovian environment due to the changes in the policies of the other agents, a non-decaying learning rate 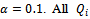 functions are initialized to
functions are initialized to  . During learning, each agent picks a random action with probability of 0.01, and otherwise its currently best action as indicated by its
. During learning, each agent picks a random action with probability of 0.01, and otherwise its currently best action as indicated by its  function (cf. Equation 14).Part (c) of Figure 2 provides a snapshot from the track while the learning process is going on. Every time the system has entered a jamming state, the simulation is reset and the learning process continues again from the initial situation with all vehicles distributed equidistantly. As can be seen, the number of simulation steps until the collective of agents runs into a jam is increasing as learning proceeds.
function (cf. Equation 14).Part (c) of Figure 2 provides a snapshot from the track while the learning process is going on. Every time the system has entered a jamming state, the simulation is reset and the learning process continues again from the initial situation with all vehicles distributed equidistantly. As can be seen, the number of simulation steps until the collective of agents runs into a jam is increasing as learning proceeds. | Figure 3. Online learning progress for a setting with 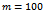 independent learning agents: The vehicle controlling behavior of the Krauss model is clearly outperformed. Noise level: independent learning agents: The vehicle controlling behavior of the Krauss model is clearly outperformed. Noise level: 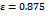 |
Figure 3 summarizes the development of the traffic flow, i.e. the average velocity of all vehicles, during a typical learning run for 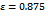 . As already said, at the beginning of learning the traffic flow breaks down due to the emergence of a jam, but after approximately 2000 simulation steps the agents have successfully learned to prevent jams from occurring any further. Note that in a single time step each agent does an individual update to the shared data structure storing the
. As already said, at the beginning of learning the traffic flow breaks down due to the emergence of a jam, but after approximately 2000 simulation steps the agents have successfully learned to prevent jams from occurring any further. Note that in a single time step each agent does an individual update to the shared data structure storing the 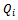 function. Thus, because we have
function. Thus, because we have 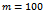 agents, this plot corresponds to a total of 500k updates to the local state-action value function.On the one hand, this is a strong result as it indicates that the agents have learned in which situations it is advisable to drive less aggressively and to no further increase their speed. On the other hand, this more farsighted driving policy stabilizes the average velocity at about
agents, this plot corresponds to a total of 500k updates to the local state-action value function.On the one hand, this is a strong result as it indicates that the agents have learned in which situations it is advisable to drive less aggressively and to no further increase their speed. On the other hand, this more farsighted driving policy stabilizes the average velocity at about 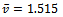 which is 16.1% above the value
which is 16.1% above the value 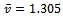 achieved in the standard Krauss model under the same settings (cf. Figure 1, right).In Figure 4 an excerpt of the resulting vehicle controlling policy, derived greedily from the learned state-action value function, is plotted. The state space to be considered by the agents is three-dimensional, so the figure plots, for six different values of the vehicle's own velocity the optimal action subject to the preceding vehicle's current velocity and the gap between the vehicle at hand and its predecessor. The two actions available to the agent (
achieved in the standard Krauss model under the same settings (cf. Figure 1, right).In Figure 4 an excerpt of the resulting vehicle controlling policy, derived greedily from the learned state-action value function, is plotted. The state space to be considered by the agents is three-dimensional, so the figure plots, for six different values of the vehicle's own velocity the optimal action subject to the preceding vehicle's current velocity and the gap between the vehicle at hand and its predecessor. The two actions available to the agent (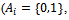 cf. Definition 4) are shown in different shades of gray (light: accelerate, dark: do not accelerate).
cf. Definition 4) are shown in different shades of gray (light: accelerate, dark: do not accelerate). 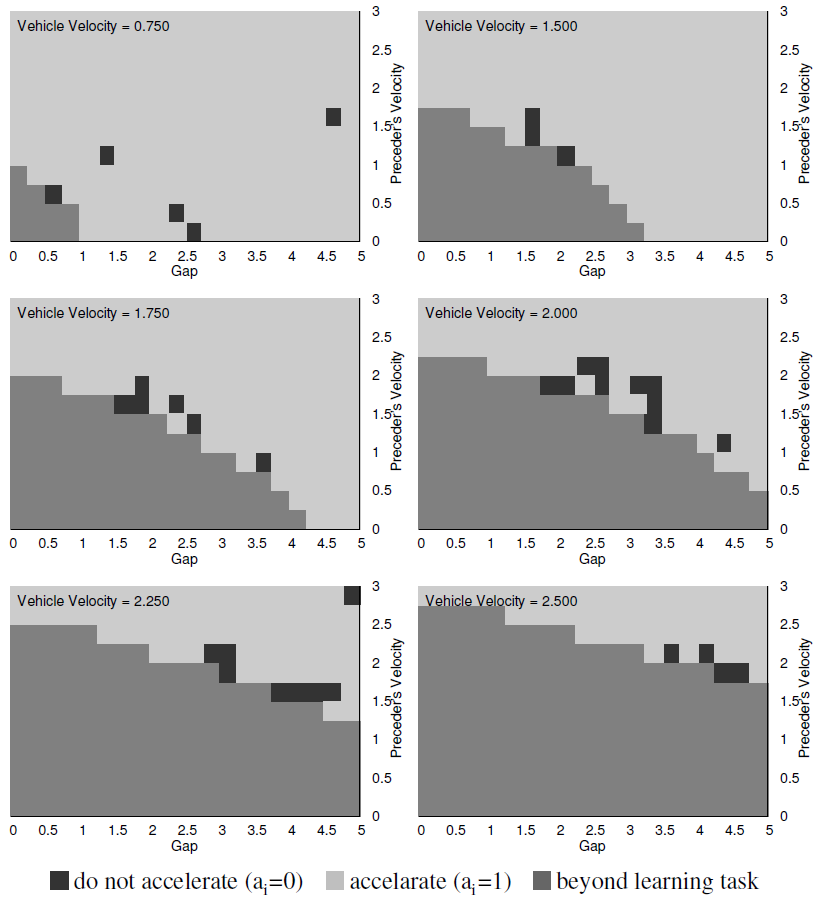 | Figure 4. Part of the local driving policy acquired: The agents have discovered regions of  where it is advantageous to behave less selfishly and accelerate no further (dark gray). This cautiousness prevents traffic jams from emerging where it is advantageous to behave less selfishly and accelerate no further (dark gray). This cautiousness prevents traffic jams from emerging |
Clearly, in the Krauss model – and, hence, by human drivers – the action “accelerate” would be chosen in any situation. The adaptive agents, by contrast, have figured out those regions of the abstract state space in which it is better to no further accelerate their current velocity (entries in dark gray). This cautiousness prevents traffic jams from emerging. Note that the medium gray regions are beyond the scope of the learning task as they cannot be entered due to the dynamics of the Krauss model. For example, those states correspond to situations that would violate the guarantee of motion without collision in the Krauss model.The traffic patterns that arise when the learned joint policy is applied in the simulation are shown in part (d) of Figure 4. The behavior of the drivers is now less selfish, possibly a little more conservative and, as a consequence, no longer yields traffic jams (tested for  simulation steps). If, due to the challenging level of noise (
simulation steps). If, due to the challenging level of noise ( , minor congestions emerge, then these can be resolved and do not lead to a jam – instead a homogeneous, constant flow is attained. This also comes along with a
, minor congestions emerge, then these can be resolved and do not lead to a jam – instead a homogeneous, constant flow is attained. This also comes along with a 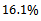 gain in terms of increased average vehicle velocity as pointed out above.We also investigated the even more challenging task of applying the learned driving policy to different noise levels
gain in terms of increased average vehicle velocity as pointed out above.We also investigated the even more challenging task of applying the learned driving policy to different noise levels 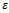 , i.e. to situations for which it was actually not trained. Most notably, the acquired policy outperforms the standard Krauss behavior as it reliably prevents jams from emerging for all noise values
, i.e. to situations for which it was actually not trained. Most notably, the acquired policy outperforms the standard Krauss behavior as it reliably prevents jams from emerging for all noise values 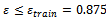 . Beyond this, for noise levels not too unsimilar from
. Beyond this, for noise levels not too unsimilar from 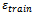 there is also a gain in terms of increased traffic flow (printed in bold in Table 1).
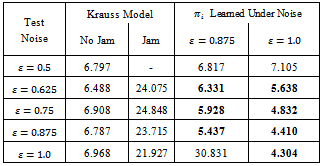
there is also a gain in terms of increased traffic flow (printed in bold in Table 1).Table 1. Learning results for different noise levels during learning and during the application of the learned policy
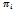 are contrasted to the traffic patterns arising under the standard Krauss model. The learners are successful in preventing traffic jams (jam: •, no jam: o) and in achieving high average vehicle velocities (recall that are contrasted to the traffic patterns arising under the standard Krauss model. The learners are successful in preventing traffic jams (jam: •, no jam: o) and in achieving high average vehicle velocities (recall that
 ), when compared to the standard Krauss model ), when compared to the standard Krauss model
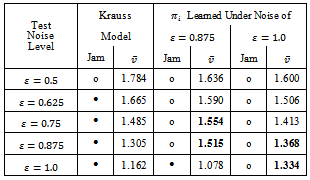 |
| |
|
We repeated the entire series of experiments also for an even larger noise level during training 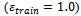 and achieved comparably convincing results: The trained agents reliably avoid jams for any noise level they are faced with. Moreover, they yield higher traffic flows than the standard Krauss behavior for values of
and achieved comparably convincing results: The trained agents reliably avoid jams for any noise level they are faced with. Moreover, they yield higher traffic flows than the standard Krauss behavior for values of 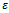 that are equal or slightly smaller than the noise present during the training phase.A secondary measure which might be easily derived from the driving behavior of the agents is their fuel consumption (and, hence, their emission of fumes). We employ a straightforward estimation of fuel consumption according to
that are equal or slightly smaller than the noise present during the training phase.A secondary measure which might be easily derived from the driving behavior of the agents is their fuel consumption (and, hence, their emission of fumes). We employ a straightforward estimation of fuel consumption according to 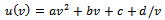 where
where 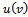 denotes the fuel usage per distance subject to the velocity
denotes the fuel usage per distance subject to the velocity 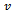 of the vehicle. Clearly, the constants in this simple model would have to be fitted to the parameters of the vehicles as well as to external factors. For a rough estimation that fits our simulation setting, we employ
of the vehicle. Clearly, the constants in this simple model would have to be fitted to the parameters of the vehicles as well as to external factors. For a rough estimation that fits our simulation setting, we employ 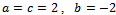 , and
, and 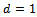 . Thus, for example, driving constantly at
. Thus, for example, driving constantly at 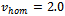 , a vehicle consumes
, a vehicle consumes 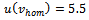 fuel units for passing the track of length
fuel units for passing the track of length 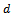 .Table 2 summarizes the fuel consumption levels for different noise levels in the standard Krauss model under free flow (e.g. at the beginning of a simulation) and when a jam has emerged (as in Figure 3b).When comparing to the fuel consumed by the vehicles controlled by the adaptive agents, we observe a significant reduction of fuel usage which can be tributed to two key facts: On the one hand, the learning agents aim at preventing the emergence of traffic jams. Since jams are the main reason for excessive fuel usage, to this end a substantial advantage is achieved. On the other hand, the learners also acquire a smooth and less aggressive driving behavior which, by default, also lowers fuel consumption in free flow. This, of course, comes along with slightly smaller average vehicle velocities compared to the ones attained by the standard Krauss model (cf. Table 1).
.Table 2 summarizes the fuel consumption levels for different noise levels in the standard Krauss model under free flow (e.g. at the beginning of a simulation) and when a jam has emerged (as in Figure 3b).When comparing to the fuel consumed by the vehicles controlled by the adaptive agents, we observe a significant reduction of fuel usage which can be tributed to two key facts: On the one hand, the learning agents aim at preventing the emergence of traffic jams. Since jams are the main reason for excessive fuel usage, to this end a substantial advantage is achieved. On the other hand, the learners also acquire a smooth and less aggressive driving behavior which, by default, also lowers fuel consumption in free flow. This, of course, comes along with slightly smaller average vehicle velocities compared to the ones attained by the standard Krauss model (cf. Table 1).Table 2. Approximate levels of fuel consumption for varying noise level. Compared to the consumption in the standard Krauss model fuel usage is heavily reduced, if the vehicles employ the learned policies
 |
| |
|
5. Conclusions and Future Work
In this article, we have proposed a novel multi-agent learning approach to microscopic traffic flow control. We have provided both a formal grounding of the approach taken as well as an empirical evaluation of its properties. The latter has shown that a significant improvement of traffic quality – in terms of jam prevention, flow optimization, and fuel consumption minimization – can be achieved, if the selfish behavior of human drivers is replaced by the vehicle controlling policies learned by the agents.Our study opens a number of opportunities for interesting directions of future research. The online learning algorithm we were using deals wastefully with the training data it collects. To this end, the utilization of state-of-the-art batch-mode reinforcement learning algorithms, which are known for their efficiency in data usage, seems promising. This point is also accompanied by the issue of using a more sophisticated approach for approximating the state-action value function. Another interesting challenge is the transfer of our ideas to a simulation with multiple lanes and passing maneuvers which are also supported by the Krauss model, as this would also increase the relevance of our approach to a practical application.
ACKNOWLEDGEMENTS
The authors would like to thank the anonymous reviewers whose comments helped considerably in improving an earlier version of this manuscript.
References
| [1] | Department for Transport, “Road Transport Forecasts 2011: Results from the Department for Transport’s National Transport Model”, United Kingdom Government, 2012. Online Available: http://dft.gov.uk/publications/road -transport-forecasts-2011 |
| [2] | M. Riedmiller, M. Montemerlo and H. Dahlkamp, “Learning to Drive in 20 Minutes”, in Proceedings of Frontiers in the Convergence of Bioscience and IT 2007 (FBIT 2007), 2007. |
| [3] | L. Pipes, “An Operational Analysis of Traffic Dynamics”, Journ. Appl. Physics, vol. 24, pp. 274-281, 1953. |
| [4] | D. Gazis, R. Herman and R. Rothery, R, “Nonlinear Follow-the-Leader Models of Traffic Flow”, Operations Research, vol. 9, pp. 545-567, 1961. |
| [5] | M. Bando, K. Hasebe, A. Nakayama, A. Shibata and Y. Sugiyama, “Structure Stability of Congestion in Traffic Dynamics”, Japan Journal of Industrial Applied Mathematics, vol. 11, no. 2, pp. 203-223, 1994. |
| [6] | P. Gipps, “A Behavioral Car Following Model for Computer Simulation”, Transportation Research Part B: Methodological, vol. 15, no. 2, pp. 105-111, 1981. |
| [7] | S. Yukawa and M. Kikuchi, “Coupled-Map Modeling of One-Dimensional Traffic Flow”, Journal of the Physical Society of Japan, vol. 65, no. 4, pp. 916-919, 1996. |
| [8] | K. Nagel and M. Schreckenberg, “A Cellular Automaton Model for Freeway Traffic”, Journal de Physique I, vol. 2, no. 12, pp. 2221-2229, 1992. |
| [9] | S. Krauss, “Microscopic Modeling of Traffic Flow: Collision Free Vehicle Dynamics”, Ph.D. thesis, University of Cologne, Germany, 1998. |
| [10] | D. Bernstein, D. Givan, N. Immerman and S. Zilberstein, “The Complexity of Decentralized Control of Markov Decision Processes”, Mathematics of Operations Research, vol. 27, no. 4, pp. 819-840, 2002. |
| [11] | T. Gabel and M. Riedmiller, “Reinforcement Learning for DEC-MDPs with Changing Action Sets and Partially Ordered Dependencies”, in Proceedings of the 7th International Conference on Autonomous Agents and Multi-Agent Systems (AAMAS 2008), 2008. |
| [12] | D. Bernstein, R. Givan, N. Immerman and S. Zilberstein, “The Complexity of Decentralized Control of Markov Decision Processes”, in Proceedings of the 16th Conference in Uncertainty in Artificial Intelligence (UAI 2000), pp. 32-37, 2000. |
| [13] | R. Sutton and A. Barto, “Reinforcement Learning. An Introduction”, MIT Press / A Bradford Book, Cambridge, USA, 1998. |
| [14] | C. Watkins and P. Dayan, “Q-Learning”, Machine Learning, vol. 8, pp. 279-292, 1992. |
 does not coincide with the corresponding driver's desired velocity
does not coincide with the corresponding driver's desired velocity  . The latter may be subject to physical limits, safety considerations, as well as legal regulations. Most of the classical car-following models can be traced back to the rather simple idea that a driver aims at reaching a desired velocity by using
. The latter may be subject to physical limits, safety considerations, as well as legal regulations. Most of the classical car-following models can be traced back to the rather simple idea that a driver aims at reaching a desired velocity by using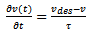
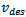 and
and 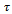 [3,4,5]. What is common to these classical models is that they determine vehicle velocities by solving differential equations. Another approach, called coupled map or cellular automata modeling, follows the idea to calculate vehicle velocities in discrete time steps, taking the situation in the preceding step into account to determine the velocities in the successor state[6,7]. This modeling approach features the advantage of being computationally efficient. Moreover, it is attractive from an agent-based perspective as it centers the focus on the individual vehicle or some kind of agent residing in it, enabling it to explicitly and autonomously act within the environment.The probably most important representative of this class of models is the Nagel-Schreckenberg model[8] which decomposes the road into segments of fixed length, allows each cell to be empty or occupied, and represents the velocity by an integer that indicates the number of cells a vehicle passes in a single time step. The model also incorporates stochasticity to account for imperfection in modeling driver behavior and, most importantly, very well simulates real traffic conditions including situations of traffic congestion.
[3,4,5]. What is common to these classical models is that they determine vehicle velocities by solving differential equations. Another approach, called coupled map or cellular automata modeling, follows the idea to calculate vehicle velocities in discrete time steps, taking the situation in the preceding step into account to determine the velocities in the successor state[6,7]. This modeling approach features the advantage of being computationally efficient. Moreover, it is attractive from an agent-based perspective as it centers the focus on the individual vehicle or some kind of agent residing in it, enabling it to explicitly and autonomously act within the environment.The probably most important representative of this class of models is the Nagel-Schreckenberg model[8] which decomposes the road into segments of fixed length, allows each cell to be empty or occupied, and represents the velocity by an integer that indicates the number of cells a vehicle passes in a single time step. The model also incorporates stochasticity to account for imperfection in modeling driver behavior and, most importantly, very well simulates real traffic conditions including situations of traffic congestion.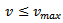 , while at the same time it is assumed that a driver desires to move as fast as possible. Thus, in free flow,
, while at the same time it is assumed that a driver desires to move as fast as possible. Thus, in free flow, 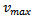 is the desired velocity
is the desired velocity 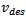 of a driver.Concerning motion while interacting with other vehicles, any driver's primary incentive is to avoid a collision with a preceding vehicle. To this end, Krauss makes the central assumption that any motion is free of collisions. As a consequence, drivers are constrained to always limit their velocity to a value
of a driver.Concerning motion while interacting with other vehicles, any driver's primary incentive is to avoid a collision with a preceding vehicle. To this end, Krauss makes the central assumption that any motion is free of collisions. As a consequence, drivers are constrained to always limit their velocity to a value 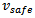 that guarantees breaking to a full stop while not colliding with the preceding vehicle, i.e. it always holds
that guarantees breaking to a full stop while not colliding with the preceding vehicle, i.e. it always holds 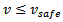 . The determination of
. The determination of 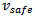 contains all the information about how vehicles interact with one another.A final assumption the Krauss model makes concerns the physical properties of the vehicles. The values of the maximal acceleration
contains all the information about how vehicles interact with one another.A final assumption the Krauss model makes concerns the physical properties of the vehicles. The values of the maximal acceleration 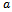 and the breaking acceleration
and the breaking acceleration 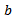 of vehicles are bounded, i.e.
of vehicles are bounded, i.e. 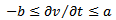 with
with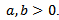 Traffic simulation in the Krauss model takes place in discrete time steps
Traffic simulation in the Krauss model takes place in discrete time steps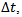 while space variables are continuous. This gives rise to the following inequation that holds true for the velocity of each vehicle:
while space variables are continuous. This gives rise to the following inequation that holds true for the velocity of each vehicle: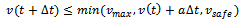
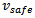 is determined with respect to the maximum breaking constraint
is determined with respect to the maximum breaking constraint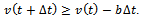
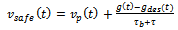
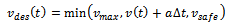
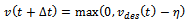
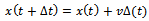
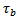 denotes the time required to come to a full stop which Krauss approximates by
denotes the time required to come to a full stop which Krauss approximates by 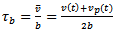
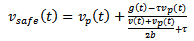
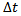 is equal to the reaction time
is equal to the reaction time 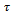 with a typical setting of
with a typical setting of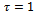 . Therefore, the length of a vehicle is not its true physical length, but the space that it covers in a dense jam, i.e. a slightly larger quantity. Putting these settings together, the formula for
. Therefore, the length of a vehicle is not its true physical length, but the space that it covers in a dense jam, i.e. a slightly larger quantity. Putting these settings together, the formula for 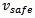 becomes
becomes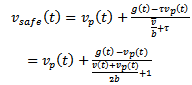
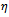 which is uniformly distributed over the interval
which is uniformly distributed over the interval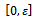 , where
, where 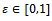 is the noise parameter of the model.
is the noise parameter of the model.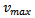 , the maximal acceleration
, the maximal acceleration 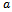 , the maximal deceleration
, the maximal deceleration 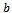 , and the noise (or lingering) parameter
, and the noise (or lingering) parameter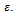 The relation of the exact values of
The relation of the exact values of 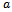 and
and 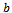 plays a crucial role as to whether a traffic flow simulation based on the Krauss model exhibits realistic properties, i.e. whether it successfully models real traffic, or not. To this end, three fundamentally different cases are distinguished[9] which result in qualitatively different types of behavior: • the high acceleration limit with
plays a crucial role as to whether a traffic flow simulation based on the Krauss model exhibits realistic properties, i.e. whether it successfully models real traffic, or not. To this end, three fundamentally different cases are distinguished[9] which result in qualitatively different types of behavior: • the high acceleration limit with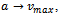 • the high deceleration limit with
• the high deceleration limit with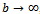 , and • the low acceleration, low deceleration setting with
, and • the low acceleration, low deceleration setting with 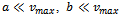 . However, only model instances of the third type exhibit macroscopically realistic behavior and, hence, describe real traffic in a qualitatively accurate way. For example, only in this setting jams feature a stable outflow and they arise “out of nothing”, i.e. the phase transition-like occurrence of jams is present. In essence, the Krauss model is capable of simulating real-world traffic well, if the acceleration and deceleration are limited to values that correspond to realistic vehicle dynamics. Clearly, we stick to such a setting in the remainder of this article.In order to realize a realistic model of jamming two basic ingredients must be given[9]. On the one hand, vehicles must be able to slow down to a velocity slower than that of the leading car. On the other hand, the outflow from traffic congestions must be lower than the maximum flow. In the traffic flow model under consideration both of these characteristics are implemented by the noise term (cf.
. However, only model instances of the third type exhibit macroscopically realistic behavior and, hence, describe real traffic in a qualitatively accurate way. For example, only in this setting jams feature a stable outflow and they arise “out of nothing”, i.e. the phase transition-like occurrence of jams is present. In essence, the Krauss model is capable of simulating real-world traffic well, if the acceleration and deceleration are limited to values that correspond to realistic vehicle dynamics. Clearly, we stick to such a setting in the remainder of this article.In order to realize a realistic model of jamming two basic ingredients must be given[9]. On the one hand, vehicles must be able to slow down to a velocity slower than that of the leading car. On the other hand, the outflow from traffic congestions must be lower than the maximum flow. In the traffic flow model under consideration both of these characteristics are implemented by the noise term (cf. 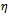 in Equation (6)) which is subject to the noise parameter
in Equation (6)) which is subject to the noise parameter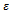 .Let us consider the first of these two features in more detail. The noise term implements overreactions that destabilize dense traffic. Drivers slow down their velocity to a value lower than necessary. This can lead to the emergence of a jam, where the probability for this to happen increases with the density of the traffic. Krauss points out that for any value of the noise parameter there is a value of the traffic's density, where the traffic typically breaks down due to the drivers' overreactions modeled by
.Let us consider the first of these two features in more detail. The noise term implements overreactions that destabilize dense traffic. Drivers slow down their velocity to a value lower than necessary. This can lead to the emergence of a jam, where the probability for this to happen increases with the density of the traffic. Krauss points out that for any value of the noise parameter there is a value of the traffic's density, where the traffic typically breaks down due to the drivers' overreactions modeled by 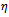 . This breakdown comes along with a reduction of the average flow of traffic – which is the average number of vehicles passing a fixed section within a given time interval – and can be characterized by the difference of the homogeneous flow and the flow in a jammed state. While this difference vanishes for small noise values, it grows to a substantial amount as
. This breakdown comes along with a reduction of the average flow of traffic – which is the average number of vehicles passing a fixed section within a given time interval – and can be characterized by the difference of the homogeneous flow and the flow in a jammed state. While this difference vanishes for small noise values, it grows to a substantial amount as 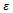 becomes larger than 0.5. In other words, for a fixed traffic density and small values of
becomes larger than 0.5. In other words, for a fixed traffic density and small values of 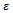 (and, in particular, for the noise-free setting
(and, in particular, for the noise-free setting 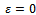 ) the entire traffic flow is deterministic and the model degenerates to a simulation that remains unchangeably in a state of constant flow. Consequently, to allow for a meaningful simulation and to allow for a realistic occurrence and analysis of jams, the noise parameter must be set to reasonably large values.
) the entire traffic flow is deterministic and the model degenerates to a simulation that remains unchangeably in a state of constant flow. Consequently, to allow for a meaningful simulation and to allow for a realistic occurrence and analysis of jams, the noise parameter must be set to reasonably large values.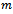 -agent DEC-MDP
-agent DEC-MDP 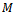 is defined by a tuple
is defined by a tuple with•
with•  as the set of agents,•
as the set of agents,•  as the set of world states which can be factored into
as the set of world states which can be factored into 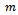 components
components 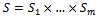 (the
(the  belong to one of the agents each)• and
belong to one of the agents each)• and  as the set of joint actions to be performed by the agents (
as the set of joint actions to be performed by the agents ( denotes a joint action that is made up of elementary actions
denotes a joint action that is made up of elementary actions 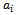 taken by agent
taken by agent 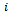 ).•
).• 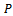 is the transition function with
is the transition function with 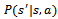 denoting the probability that the system arrives at state
denoting the probability that the system arrives at state 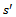 upon executing
upon executing 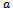 in
in 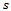 and•
and• 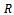 is the reward function with
is the reward function with 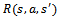 denoting the reward for executing
denoting the reward for executing 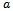 in
in 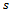 and transitioning to
and transitioning to 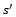 .•
.• 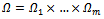 represents the set of all observations of all agents (
represents the set of all observations of all agents ( denotes a joint observation with
denotes a joint observation with 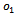 as the observation for agent
as the observation for agent 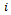 ) and•
) and• 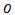 is the observation function that determines the probability
is the observation function that determines the probability 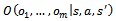 that agent 1 through
that agent 1 through 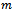 perceive observations
perceive observations 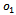 through
through 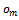 upon the execution of
upon the execution of 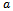 in
in 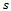 and entering
and entering 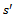 .•
.• 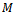 s jointly fully observable, i.e. the current state is fully determined by the amalgamation of all agents' observations:
s jointly fully observable, i.e. the current state is fully determined by the amalgamation of all agents' observations: 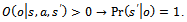 To the agent-specific components,
To the agent-specific components, 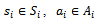 ,
, 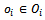 we refer as local state, local action, and local observation of agent
we refer as local state, local action, and local observation of agent 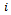 , respectively.A joint policy
, respectively.A joint policy 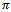 is a set of local policies
is a set of local policies 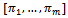 each of which is, in the general case, a mapping from agent
each of which is, in the general case, a mapping from agent 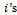 sequence of local observations to local actions, i.e.
sequence of local observations to local actions, i.e. 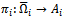 . In a memoryless, reactive setting, local policies are defined over the most recent observation only, i.e.
. In a memoryless, reactive setting, local policies are defined over the most recent observation only, i.e. 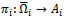 .A practically relevant case, however, is when each agent can fully observe its local state.Definition 2. A factored
.A practically relevant case, however, is when each agent can fully observe its local state.Definition 2. A factored 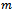 -agent DEC-MDP has local full observability, if for all agents
-agent DEC-MDP has local full observability, if for all agents 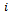 and for all local observations
and for all local observations 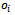 there is a local state
there is a local state 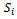 such that
such that 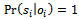 .It is important to note that joint full observability together with local full observability of a decentralized MDP do generally not imply full observability. Instead, vast parts of the global state are hidden from each of the agents[11].We also need to characterize the problems of our interest with respect to the inter-agent dependencies in their reward, transition, and observation functions. A factored
.It is important to note that joint full observability together with local full observability of a decentralized MDP do generally not imply full observability. Instead, vast parts of the global state are hidden from each of the agents[11].We also need to characterize the problems of our interest with respect to the inter-agent dependencies in their reward, transition, and observation functions. A factored 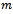 -agent DEC-MDP is called reward independent, if there exist local functions
-agent DEC-MDP is called reward independent, if there exist local functions 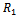 through
through 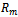 , each depending on local states and actions of the agents only, as well as a function
, each depending on local states and actions of the agents only, as well as a function 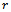 that amalgamates the global reward value from the local ones, such that maximizing each
that amalgamates the global reward value from the local ones, such that maximizing each 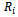 individually also yields a maximization of
individually also yields a maximization of 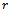 .If, in a factored
.If, in a factored 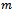 -agent DEC-MDP, the observation each agent sees depends only on its current and next local state and on its action, then the corresponding DEC-MDP is called observation independent, i.e.
-agent DEC-MDP, the observation each agent sees depends only on its current and next local state and on its action, then the corresponding DEC-MDP is called observation independent, i.e. . Then, in combination with local full observability, the observation-related components
. Then, in combination with local full observability, the observation-related components  and
and 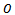 are redundant and can be removed from Definition 2.The DEC-MDPs we consider subsequently are observation and reward independent, but they are not transition independent. Hence, the state transition probabilities of one agent are in general also influenced by other agents. However, in what follows, we assume that there are certain regularities in the dependencies between the agents. In particular, the local action of agent
are redundant and can be removed from Definition 2.The DEC-MDPs we consider subsequently are observation and reward independent, but they are not transition independent. Hence, the state transition probabilities of one agent are in general also influenced by other agents. However, in what follows, we assume that there are certain regularities in the dependencies between the agents. In particular, the local action of agent 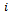 affects its own local state as well as the local state of exactly one other (always the same) agent
affects its own local state as well as the local state of exactly one other (always the same) agent 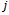 . This gives rise to the following definition.Definition 3. A factored
. This gives rise to the following definition.Definition 3. A factored 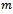 -agent DEC-MDP has circular transition dependencies, if the local state of agent
-agent DEC-MDP has circular transition dependencies, if the local state of agent 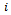 is influenced by the local action of itself as well as by the local action of agent
is influenced by the local action of itself as well as by the local action of agent 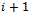 for all
for all 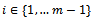 and by the local action of agent
and by the local action of agent 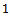 for
for 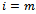 .
.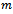 -agent DEC-MDPs with circular dependencies because:• The state of the road, i.e. the global world state is factored where each vehicle observes only a small fraction of it. We attach to each vehicle an agent
-agent DEC-MDPs with circular dependencies because:• The state of the road, i.e. the global world state is factored where each vehicle observes only a small fraction of it. We attach to each vehicle an agent 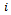 whose local state can be described by the observations that individual vehicles get hold of in the Krauss model.• State transitions are non-deterministic for a noise level
whose local state can be described by the observations that individual vehicles get hold of in the Krauss model.• State transitions are non-deterministic for a noise level 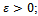 the system model is not known by the agents.• The local state
the system model is not known by the agents.• The local state 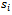 is fully described by its velocity, the velocity of its preceding vehicle as well as the gap between the two. These are the variables necessary in the Krauss model to calculate the current value of the safe velocity
is fully described by its velocity, the velocity of its preceding vehicle as well as the gap between the two. These are the variables necessary in the Krauss model to calculate the current value of the safe velocity 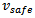 (cf. Equation 10). The combination of all local states fully identifies the global system state, i.e. the problem is a DEC-MDP, and not a DEC-POMDP.The local state space of each agent
(cf. Equation 10). The combination of all local states fully identifies the global system state, i.e. the problem is a DEC-MDP, and not a DEC-POMDP.The local state space of each agent 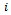 is a real-valued three-dimensional vector, i.e.
is a real-valued three-dimensional vector, i.e. 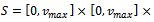
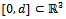 with
with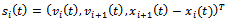
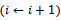 specified in Definition 3.• Given a fixed traffic density
specified in Definition 3.• Given a fixed traffic density 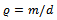 (with
(with 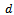 denoting the length of the track considered and
denoting the length of the track considered and 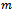 the number of vehicles), the traffic flow is defined as
the number of vehicles), the traffic flow is defined as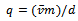 with
with 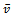 indicating the average velocity of all vehicles. Rewriting this equation, we see that it holds
indicating the average velocity of all vehicles. Rewriting this equation, we see that it holds 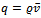 , which hints to the fact that the global traffic flow is proportional to the average velocity
, which hints to the fact that the global traffic flow is proportional to the average velocity 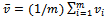 of the vehicles, given a fixed traffic density, i.e. a constant number of
of the vehicles, given a fixed traffic density, i.e. a constant number of 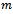 vehicles on the track. As a consequence, the corresponding DEC-MDP can be constructed to be reward-independent, if we associate the differences between the velocities of individual vehicles in their next and current time step with the local reward functions
vehicles on the track. As a consequence, the corresponding DEC-MDP can be constructed to be reward-independent, if we associate the differences between the velocities of individual vehicles in their next and current time step with the local reward functions 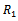 through
through 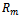 , i.e.
, i.e. 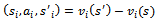 and use
and use 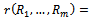
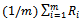 as amalgamation function (cf. Definition 1).All vehicles are independent of one another. They do not communicate with one another and choose their driving behavior independently. In the Krauss model each driver increments selfishly the desired velocity
as amalgamation function (cf. Definition 1).All vehicles are independent of one another. They do not communicate with one another and choose their driving behavior independently. In the Krauss model each driver increments selfishly the desired velocity 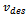 , until
, until 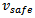 or
or 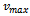 are reached. In order to allow for cooperative behavior, each agent must be enabled to willingly decide to not increase its current velocity as much as it possibly could, considering the current traffic situation.To this end, we facilitate each agent with the degree of freedom to select its desired velocity
are reached. In order to allow for cooperative behavior, each agent must be enabled to willingly decide to not increase its current velocity as much as it possibly could, considering the current traffic situation.To this end, we facilitate each agent with the degree of freedom to select its desired velocity 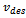 according to
according to 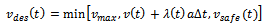
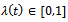 determines the share of the acceleration capabilities that the agent uses in the current time step. Thus, the choice for a concrete value of
determines the share of the acceleration capabilities that the agent uses in the current time step. Thus, the choice for a concrete value of 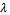 must be done in each time step and, accordingly, corresponds to the current action of the agent considered. Based on this we define the agents' local policies as follows.Definition 4. Given a factored
must be done in each time step and, accordingly, corresponds to the current action of the agent considered. Based on this we define the agents' local policies as follows.Definition 4. Given a factored 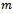 -agent DEC-MDP with circular transition dependencies, a local reactive policy of agent
-agent DEC-MDP with circular transition dependencies, a local reactive policy of agent 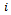 is defined as a mapping
is defined as a mapping 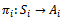 where
where 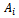 is a finite subset of
is a finite subset of 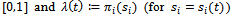 is used in update Equation 12.In the remainder of this article, we set
is used in update Equation 12.In the remainder of this article, we set 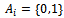 for all
for all 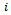 , which means that at any time step each agent can choose between a full acceleration as determined by Equation 5 and a steady motion, i.e. not to alter its current velocity. Note, however, that the velocity of an agent is still subject to the noise term (cf. Equation 7) and may, thus, be decreased randomly. More fine-grained or even continuous action sets might be employed, too, and would allow for an even higher degree of velocity control by the agent. This is subject of future work.
, which means that at any time step each agent can choose between a full acceleration as determined by Equation 5 and a steady motion, i.e. not to alter its current velocity. Note, however, that the velocity of an agent is still subject to the noise term (cf. Equation 7) and may, thus, be decreased randomly. More fine-grained or even continuous action sets might be employed, too, and would allow for an even higher degree of velocity control by the agent. This is subject of future work.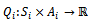 according to
according to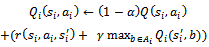
 [14]. The learning rate is denoted by
[14]. The learning rate is denoted by  , the discount factor by
, the discount factor by 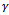 . For the case of finite state and action spaces where the Q function can be represented using a look-up table, there are convergence guarantees that say Q learning converges to the optimal state-action value function with probability one, assuming that all state-action pairs are visited infinitely often and that the learning rate
. For the case of finite state and action spaces where the Q function can be represented using a look-up table, there are convergence guarantees that say Q learning converges to the optimal state-action value function with probability one, assuming that all state-action pairs are visited infinitely often and that the learning rate  diminishes appropriately. From a given state-action value function
diminishes appropriately. From a given state-action value function 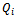 a greedy policy can be derived according to
a greedy policy can be derived according to 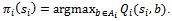
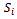 to be considered by the agents is continuous, we employ a straightforward regular grid in order to discretize
to be considered by the agents is continuous, we employ a straightforward regular grid in order to discretize 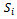 . To this end, we decompose the first state variable (relating to the vehicle's velocity) into 41 different values, the second one (preceding vehicle's velocity) into 21 values, and the third one (the gap between the two) into 21 values, giving rise to an abstract state space made up of
. To this end, we decompose the first state variable (relating to the vehicle's velocity) into 41 different values, the second one (preceding vehicle's velocity) into 21 values, and the third one (the gap between the two) into 21 values, giving rise to an abstract state space made up of 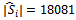 abstract states.For the time being, we grant all agents access to the same
abstract states.For the time being, we grant all agents access to the same 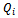 table, i.e. to the same data structure. This approach allows for a tremendous speed-up of the learning process as the experience tuples and belonging Q updates according to Equation 13 work on the same function
table, i.e. to the same data structure. This approach allows for a tremendous speed-up of the learning process as the experience tuples and belonging Q updates according to Equation 13 work on the same function  . Note that this, in principle, could enable the agents to get access to the other agents'
. Note that this, in principle, could enable the agents to get access to the other agents' 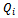 (because
(because 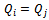 for all
for all 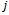 ) function and, thus, to their local policies
) function and, thus, to their local policies 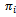 . However, this knowledge is not exploited during the learning process at all, i.e. our learning agents do not use
. However, this knowledge is not exploited during the learning process at all, i.e. our learning agents do not use 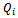 to draw conclusions regarding the other vehicles' behavior. In other words, we utilize a shared local state-action value function
to draw conclusions regarding the other vehicles' behavior. In other words, we utilize a shared local state-action value function 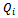 only for reasons of computational efficiency.In this regard, one might object that the coupling of all agents' local state-action value functions contradicts the idea of entirely independent and decoupled learners. Nevertheless, this approach is meaningful and of high practical relevance for several reasons: First, the agents still must act under extreme restrictions with respect to the global system state – they know only about the local traffic situation
only for reasons of computational efficiency.In this regard, one might object that the coupling of all agents' local state-action value functions contradicts the idea of entirely independent and decoupled learners. Nevertheless, this approach is meaningful and of high practical relevance for several reasons: First, the agents still must act under extreme restrictions with respect to the global system state – they know only about the local traffic situation 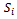 at their current location and they know nothing about the local state of other agents. Second, they do not know which actions were taken by the other agents (in fact, we disallow the agents to draw corresponding conclusions), and, as a matter of fact, even if they knew, this would be of little use because they are clueless about the local states other agents are in. Third, when thinking about a real-world implementation of a reinforcement learning approach for traffic flow optimization, it is standing to reason that the participating vehicles collect and transmit their transition data to a centralized entity (e.g. the manufacturer of certain vehicles or even a public traffic control institution), which distributes learned (and fixed)
at their current location and they know nothing about the local state of other agents. Second, they do not know which actions were taken by the other agents (in fact, we disallow the agents to draw corresponding conclusions), and, as a matter of fact, even if they knew, this would be of little use because they are clueless about the local states other agents are in. Third, when thinking about a real-world implementation of a reinforcement learning approach for traffic flow optimization, it is standing to reason that the participating vehicles collect and transmit their transition data to a centralized entity (e.g. the manufacturer of certain vehicles or even a public traffic control institution), which distributes learned (and fixed) 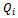 functions to all agents and lets the agents derive their local policies from this local state-action value function independently.
functions to all agents and lets the agents derive their local policies from this local state-action value function independently.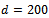 units in length that is populated with
units in length that is populated with 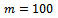 vehicles, where we start the simulation with all vehicles distributed equidistantly over the track with no initial velocity. Thus, for all
vehicles, where we start the simulation with all vehicles distributed equidistantly over the track with no initial velocity. Thus, for all 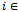
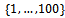 we have a gap
we have a gap 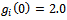 and initial velocities
and initial velocities 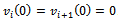 . Furthermore, we employ the settings of the acceleration and deceleration that Krauss identified to belong to the class of the “low acceleration, low deceleration” limit simulations
. Furthermore, we employ the settings of the acceleration and deceleration that Krauss identified to belong to the class of the “low acceleration, low deceleration” limit simulations 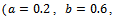
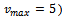 which, in general, yield the most realistic simulation.For ease of notion, we subsequently refer to the average velocity
which, in general, yield the most realistic simulation.For ease of notion, we subsequently refer to the average velocity 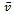 of all vehicles, when speaking about traffic flow
of all vehicles, when speaking about traffic flow 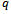 , because these two variables are proportional to one another (
, because these two variables are proportional to one another (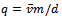 ). Speaking about realistic traffic, however, we have to clearly define what we consider to be a jamming state. Homogeneous flow – being the opposite of a jam – is characterized by all vehicles moving at constant speed under equidistant distribution over the track with a gap
). Speaking about realistic traffic, however, we have to clearly define what we consider to be a jamming state. Homogeneous flow – being the opposite of a jam – is characterized by all vehicles moving at constant speed under equidistant distribution over the track with a gap 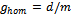 . Clearly, this state (for which it holds
. Clearly, this state (for which it holds 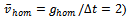 can only be attained in a noise free setting. In the remainder of this article, we say that a jam is present on the track, if• the traffic congestion results in a substantial reduction of the velocity of the cars involved, i.e. their velocity is below
can only be attained in a noise free setting. In the remainder of this article, we say that a jam is present on the track, if• the traffic congestion results in a substantial reduction of the velocity of the cars involved, i.e. their velocity is below  • the traffic congestion results in a crowding of vehicles, i.e. the gaps between the vehicles involved is below
• the traffic congestion results in a crowding of vehicles, i.e. the gaps between the vehicles involved is below 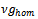 (we set
(we set 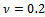 ), and• the traffic congestion is large enough, i.e. concerns at least
), and• the traffic congestion is large enough, i.e. concerns at least 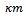 vehicles (we set
vehicles (we set 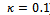 ).In Figure 1 we analyze the impact of the single remaining free parameter of the Krauss model (cf. Section 3.2), the noise or lingering parameter
).In Figure 1 we analyze the impact of the single remaining free parameter of the Krauss model (cf. Section 3.2), the noise or lingering parameter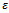 . The top chart shows for which noise levels jams emerge at all. Obviously for values of
. The top chart shows for which noise levels jams emerge at all. Obviously for values of 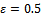 and below, traffic remains in a state of nearly homogeneous flow and the jamming conditions never occur (tested for
and below, traffic remains in a state of nearly homogeneous flow and the jamming conditions never occur (tested for 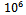 simulation steps). If we start the simulation for increasing values of
simulation steps). If we start the simulation for increasing values of 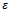 , however, the jamming state arises more and more quickly, for instance, on average after
, however, the jamming state arises more and more quickly, for instance, on average after 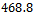 simulation steps for
simulation steps for 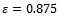 , if we start the simulation from the mentioned equidistant distribution of vehicles.The bottom part of Figure 1 visualizes to which average velocity the system converges in the long run. Apparently, for increasing noise values the flow of traffic is decreasing. It is important to note that for
, if we start the simulation from the mentioned equidistant distribution of vehicles.The bottom part of Figure 1 visualizes to which average velocity the system converges in the long run. Apparently, for increasing noise values the flow of traffic is decreasing. It is important to note that for 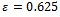 and above the equilibrium state, whose average velocity is plotted, contains a traffic jam (as indicated by the top chart).
and above the equilibrium state, whose average velocity is plotted, contains a traffic jam (as indicated by the top chart).
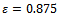 . While, initially, traffic is running smoothly, at some point of time small disturbances start to grow into significant congestions with a drop in average traffic flow. In this figure, a row of pixels shows the distribution of vehicles across the track for one instant of time (they move from left to right). With time steps increasing from top to bottom, this type of visualization captures the development of traffic flow over time. Specifically, this plot visualizes the first 700 simulation steps. Note that the varying colors of the individual vehicles are used for the purpose of better presentation only. Part b) of this figure shows the saturation state of the same scenario reached after 2000 time steps: Obviously, the system has gone into an equilibrium state with one big traffic jam and an average vehicle velocity of only
. While, initially, traffic is running smoothly, at some point of time small disturbances start to grow into significant congestions with a drop in average traffic flow. In this figure, a row of pixels shows the distribution of vehicles across the track for one instant of time (they move from left to right). With time steps increasing from top to bottom, this type of visualization captures the development of traffic flow over time. Specifically, this plot visualizes the first 700 simulation steps. Note that the varying colors of the individual vehicles are used for the purpose of better presentation only. Part b) of this figure shows the saturation state of the same scenario reached after 2000 time steps: Obviously, the system has gone into an equilibrium state with one big traffic jam and an average vehicle velocity of only 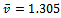 .
.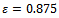 . The agents use a discount factor of
. The agents use a discount factor of 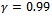 and, in order to account for the non-Markovian environment due to the changes in the policies of the other agents, a non-decaying learning rate
and, in order to account for the non-Markovian environment due to the changes in the policies of the other agents, a non-decaying learning rate 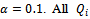 functions are initialized to
functions are initialized to 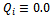 . During learning, each agent picks a random action with probability of 0.01, and otherwise its currently best action as indicated by its
. During learning, each agent picks a random action with probability of 0.01, and otherwise its currently best action as indicated by its 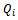 function (cf. Equation 14).Part (c) of Figure 2 provides a snapshot from the track while the learning process is going on. Every time the system has entered a jamming state, the simulation is reset and the learning process continues again from the initial situation with all vehicles distributed equidistantly. As can be seen, the number of simulation steps until the collective of agents runs into a jam is increasing as learning proceeds.
function (cf. Equation 14).Part (c) of Figure 2 provides a snapshot from the track while the learning process is going on. Every time the system has entered a jamming state, the simulation is reset and the learning process continues again from the initial situation with all vehicles distributed equidistantly. As can be seen, the number of simulation steps until the collective of agents runs into a jam is increasing as learning proceeds.
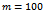 independent learning agents: The vehicle controlling behavior of the Krauss model is clearly outperformed. Noise level:
independent learning agents: The vehicle controlling behavior of the Krauss model is clearly outperformed. Noise level: 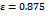
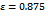 . As already said, at the beginning of learning the traffic flow breaks down due to the emergence of a jam, but after approximately 2000 simulation steps the agents have successfully learned to prevent jams from occurring any further. Note that in a single time step each agent does an individual update to the shared data structure storing the
. As already said, at the beginning of learning the traffic flow breaks down due to the emergence of a jam, but after approximately 2000 simulation steps the agents have successfully learned to prevent jams from occurring any further. Note that in a single time step each agent does an individual update to the shared data structure storing the 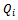 function. Thus, because we have
function. Thus, because we have 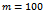 agents, this plot corresponds to a total of 500k updates to the local state-action value function.On the one hand, this is a strong result as it indicates that the agents have learned in which situations it is advisable to drive less aggressively and to no further increase their speed. On the other hand, this more farsighted driving policy stabilizes the average velocity at about
agents, this plot corresponds to a total of 500k updates to the local state-action value function.On the one hand, this is a strong result as it indicates that the agents have learned in which situations it is advisable to drive less aggressively and to no further increase their speed. On the other hand, this more farsighted driving policy stabilizes the average velocity at about 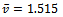 which is 16.1% above the value
which is 16.1% above the value 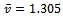 achieved in the standard Krauss model under the same settings (cf. Figure 1, right).In Figure 4 an excerpt of the resulting vehicle controlling policy, derived greedily from the learned state-action value function, is plotted. The state space to be considered by the agents is three-dimensional, so the figure plots, for six different values of the vehicle's own velocity the optimal action subject to the preceding vehicle's current velocity and the gap between the vehicle at hand and its predecessor. The two actions available to the agent (
achieved in the standard Krauss model under the same settings (cf. Figure 1, right).In Figure 4 an excerpt of the resulting vehicle controlling policy, derived greedily from the learned state-action value function, is plotted. The state space to be considered by the agents is three-dimensional, so the figure plots, for six different values of the vehicle's own velocity the optimal action subject to the preceding vehicle's current velocity and the gap between the vehicle at hand and its predecessor. The two actions available to the agent (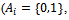 cf. Definition 4) are shown in different shades of gray (light: accelerate, dark: do not accelerate).
cf. Definition 4) are shown in different shades of gray (light: accelerate, dark: do not accelerate). 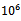 simulation steps). If, due to the challenging level of noise (
simulation steps). If, due to the challenging level of noise (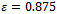 , minor congestions emerge, then these can be resolved and do not lead to a jam – instead a homogeneous, constant flow is attained. This also comes along with a
, minor congestions emerge, then these can be resolved and do not lead to a jam – instead a homogeneous, constant flow is attained. This also comes along with a 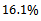 gain in terms of increased average vehicle velocity as pointed out above.We also investigated the even more challenging task of applying the learned driving policy to different noise levels
gain in terms of increased average vehicle velocity as pointed out above.We also investigated the even more challenging task of applying the learned driving policy to different noise levels 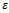 , i.e. to situations for which it was actually not trained. Most notably, the acquired policy outperforms the standard Krauss behavior as it reliably prevents jams from emerging for all noise values
, i.e. to situations for which it was actually not trained. Most notably, the acquired policy outperforms the standard Krauss behavior as it reliably prevents jams from emerging for all noise values 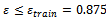 . Beyond this, for noise levels not too unsimilar from
. Beyond this, for noise levels not too unsimilar from 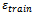 there is also a gain in terms of increased traffic flow (printed in bold in Table 1).
there is also a gain in terms of increased traffic flow (printed in bold in Table 1).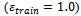 and achieved comparably convincing results: The trained agents reliably avoid jams for any noise level they are faced with. Moreover, they yield higher traffic flows than the standard Krauss behavior for values of
and achieved comparably convincing results: The trained agents reliably avoid jams for any noise level they are faced with. Moreover, they yield higher traffic flows than the standard Krauss behavior for values of 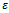 that are equal or slightly smaller than the noise present during the training phase.A secondary measure which might be easily derived from the driving behavior of the agents is their fuel consumption (and, hence, their emission of fumes). We employ a straightforward estimation of fuel consumption according to
that are equal or slightly smaller than the noise present during the training phase.A secondary measure which might be easily derived from the driving behavior of the agents is their fuel consumption (and, hence, their emission of fumes). We employ a straightforward estimation of fuel consumption according to 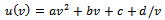 where
where 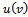 denotes the fuel usage per distance subject to the velocity
denotes the fuel usage per distance subject to the velocity 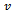 of the vehicle. Clearly, the constants in this simple model would have to be fitted to the parameters of the vehicles as well as to external factors. For a rough estimation that fits our simulation setting, we employ
of the vehicle. Clearly, the constants in this simple model would have to be fitted to the parameters of the vehicles as well as to external factors. For a rough estimation that fits our simulation setting, we employ 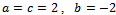 , and
, and 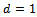 . Thus, for example, driving constantly at
. Thus, for example, driving constantly at 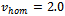 , a vehicle consumes
, a vehicle consumes 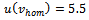 fuel units for passing the track of length
fuel units for passing the track of length 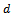 .Table 2 summarizes the fuel consumption levels for different noise levels in the standard Krauss model under free flow (e.g. at the beginning of a simulation) and when a jam has emerged (as in Figure 3b).When comparing to the fuel consumed by the vehicles controlled by the adaptive agents, we observe a significant reduction of fuel usage which can be tributed to two key facts: On the one hand, the learning agents aim at preventing the emergence of traffic jams. Since jams are the main reason for excessive fuel usage, to this end a substantial advantage is achieved. On the other hand, the learners also acquire a smooth and less aggressive driving behavior which, by default, also lowers fuel consumption in free flow. This, of course, comes along with slightly smaller average vehicle velocities compared to the ones attained by the standard Krauss model (cf. Table 1).
.Table 2 summarizes the fuel consumption levels for different noise levels in the standard Krauss model under free flow (e.g. at the beginning of a simulation) and when a jam has emerged (as in Figure 3b).When comparing to the fuel consumed by the vehicles controlled by the adaptive agents, we observe a significant reduction of fuel usage which can be tributed to two key facts: On the one hand, the learning agents aim at preventing the emergence of traffic jams. Since jams are the main reason for excessive fuel usage, to this end a substantial advantage is achieved. On the other hand, the learners also acquire a smooth and less aggressive driving behavior which, by default, also lowers fuel consumption in free flow. This, of course, comes along with slightly smaller average vehicle velocities compared to the ones attained by the standard Krauss model (cf. Table 1). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
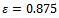

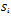 where it is advantageous to behave less selfishly and accelerate no further (dark gray). This cautiousness prevents traffic jams from emerging
where it is advantageous to behave less selfishly and accelerate no further (dark gray). This cautiousness prevents traffic jams from emerging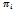 are contrasted to the traffic patterns arising under the standard Krauss model. The learners are successful in preventing traffic jams (jam: •, no jam: o) and in achieving high average vehicle velocities (recall that
are contrasted to the traffic patterns arising under the standard Krauss model. The learners are successful in preventing traffic jams (jam: •, no jam: o) and in achieving high average vehicle velocities (recall that  ), when compared to the standard Krauss model
), when compared to the standard Krauss model
