-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Traffic and Transportation Engineering
2012; 1(3): 40-45
doi: 10.5923/j.ijtte.20120103.02
Operations of Winter Maintenance of Airport
Peter Koščák 1, Štefan Berežný 2, Ján Ferenc 1
1Department of Aviation Engineering Faculty of Aeronautics Technical university of Kosice, 041 21, Slovakia, Airports Operation
2Department of Mathematics and Theoretical Informatics of Electrical Engineering and Informatics Faculty Technical university of Kosice, 041 21, Slovakia, Mathematics
Correspondence to: Peter Koščák , Department of Aviation Engineering Faculty of Aeronautics Technical university of Kosice, 041 21, Slovakia, Airports Operation.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The direct ensuring process of air transport by airport operators means to provide all components for safety landings, movements and clearance of particular flights. The mentioned factors depend on the quality and quantity of airport personnel and technical resources. Financial turnover of the airport depends on the number of flights and passengers. The higher the frequency, the higher profit items, whether it is the airport taxes or business of the company. However, to ensure regular income, the airport company has to ensure safe and regular air travel, especially without long-term and frequent limitations. These tasks are of particular importance in the winter, when the weather - snow and ice limit the effects of airfield serviceability.
Keywords: Winter Maintenance of Airport, the Optimal Deployment of Technical Means, Regression Analysism
Cite this paper: Peter Koščák , Štefan Berežný , Ján Ferenc , "Operations of Winter Maintenance of Airport", International Journal of Traffic and Transportation Engineering, Vol. 1 No. 3, 2012, pp. 40-45. doi: 10.5923/j.ijtte.20120103.02.
Article Outline
1. Introduction
- Winter maintenance of airport (WMA) must be organized and carried out in order to maintain the all weather operational capability of airport operating areas in a comprehensive, cost-effective and expedient use of people and equipment intended for winter maintenance.Composition of the WMA group must ensure continuity of the winter maintenance of the airport. Group WMA consists of a shift and the master (head) and drivers – mechanists of a single technique .
2. Snow Properties
- Formation of snow must be seen as a part of the hydrological cycle which happens in the atmosphere. Evaporation of water from the earth gets a large amount of water vapour into the atmosphere. If atmosphere is overloaded or water vapours decrease the temperature to so-called dew point, water vapours in the atmosphere condense and there is rain. If temperature is below 0 ℃, the gaseous state of water change right in the solid, recrystallization occurs. This process is linked to so-called crystallisation centres, which are ice cores or dust. Because of valence forces huge number of water molecules creates the formations of a crystal system resulting to snow crystals. The whole process can be represented as follows: saturation of water vapour + centres of crystallization + temperature < 0℃ Snow is hydroscopic and quite quickly depending on the temperature rise and its density increases. Snow density can be determined by sampling a certain volume of snow and measuring a volume of water after it melted.[1][2]
 | Figure 1. Snow at the Apron |
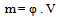 | (1) |
|
3. The Analysis of Technological Practices of Winter Maintenance of Airports
- Enforcement of activities associated with WMA depends on:●a size of the airport - the maintenance area → runway, taxiway, apron and service communications,●density of air traffic for the airport → number of movements of aviation technology for the assessment period,●an average amount of snowfall and snow under a year.Following two factors determine the staffing and technical support WMA:●whereby more movements of aviation technology, thereby reducing the time devoted to the maintenance of airport,●more snowfalls with the higher volume of snow and extensive areas of maintenance, the more frequent changes of WMA.For purposes of calculating the optimal deployment of technology to the winter maintenance of airports and the subsequent determination of the dimensions of the model airport, the following size of the airfield is used:●Runway (RWY) 3000 x 45 meters●Taxiways (TWY) - parallel taxiway with runway 3000 x 23 m + coupling paths 2 x 300 x 23 m,●Apron (APN) 200 x 100 m.Total area is 237,800 m²
 | Figure 2. Airport sweepers |
 | Figure 3. Airport’s area |
3.1. The Performance Characteristics of Technology
- Despite the technological process of disposal of snow in the movement area of airport, the performance characteristics of snow surfaces are primary rated, as the performance of airport sweeper motor is necessary to count with respect to amount and weight of removed snow. This quantity is given by the ability of snow blades to draw aside snow to the weight limits of the snow, which is affected by the technical design of airport snow blades.
3.2. The Performance Characteristics of Equipment
- Despite the technological procedure of liquidation of snow on the movement areas in order to evaluate first the performance characteristics of snow blowers, since the motor performance of airport sweepers should be counted with respect to sweep and number and weight of snow. This amount is the possibility of snow ploughs snow pushed back into the weight limits of snow, which is influenced by the technical design of airport snow ploughs. The width of snow plough of 5 or more meters in the weight of snow above 350 kg per 1 meter of purified surface width is a real threat of damage to the handle or blade or its parts.To approximate the distribution of basic snow blowers it is necessary to take into consideration their performance characteristics and engine performance, operating speed and overall performance. The techniques are divided into three performance groups listed in the Table No. 3.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Optimization of Employment of Means WMA
- As a means to solve the tasks of optimization of airport maintenance we can use fictional model of employment of proposed technique using the standard size of the international airport.We assume that we are cleaning constant size of airfields:Cleaning of the airport area can only be done by whole sets of airport technique, which is intended to winter maintenance of the airport (a kit consists of two airport motor snow blowers and one sweeper).[13]
 | Figure 4. Cache regression line and residues detected values |
 {1;2;3}, K
{1;2;3}, K 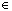 {1;2;3}, and S
{1;2;3}, and S 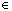 {0,03;0,06}.We created a table, which corresponds to 18 theoretical measurements for the WMA at Kosice airport by given technique.Under these assumptions and given numeric data, which are clearly shown in Table 2, we can establish a multiple linear model using the method of least squares.[14]
{0,03;0,06}.We created a table, which corresponds to 18 theoretical measurements for the WMA at Kosice airport by given technique.Under these assumptions and given numeric data, which are clearly shown in Table 2, we can establish a multiple linear model using the method of least squares.[14] 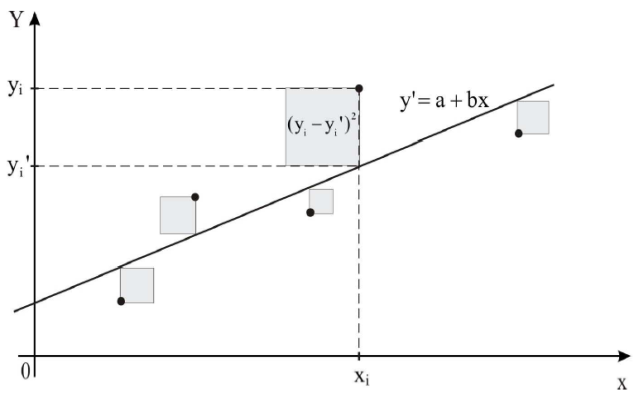 | Figure 5. The graph of the least square method for linear dependence |
|
 | (2) |
 | (3) |
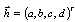 a vector →
a vector → 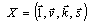 | (4) |
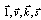 are column vectors of the size of 18x1, the
are column vectors of the size of 18x1, the 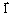 vector is a vector of the counted quantity, and
vector is a vector of the counted quantity, and 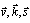 vectors and
vectors and 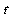 the vectors are broken down above the table.With this designation, we can then write the model described above in the form:
the vectors are broken down above the table.With this designation, we can then write the model described above in the form: 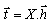 | (5) |
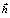 is:
is: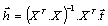 | (6) |
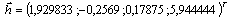 Specifically, we can write thata = 1.929853b = -0.2565c = 0.17875d = 5.944444We get a model that has the form:ti = 1,929853 – 0,2565.vi + 0,17875.ki + 5,944444.siAt first glance it may seem that this model does not describe our situation properly, because the parameter value is not zero.We could assume that if we have no snow, so WMA is the zero-time. This is not possible, because this would be contrary to the assumptions which we put to our model. In them it is stated that the variables v and k do not have zero values, i.e. if we have the snow height of 0, then maintenance takes place in non-zero time, because technique would be idle.[15]
Specifically, we can write thata = 1.929853b = -0.2565c = 0.17875d = 5.944444We get a model that has the form:ti = 1,929853 – 0,2565.vi + 0,17875.ki + 5,944444.siAt first glance it may seem that this model does not describe our situation properly, because the parameter value is not zero.We could assume that if we have no snow, so WMA is the zero-time. This is not possible, because this would be contrary to the assumptions which we put to our model. In them it is stated that the variables v and k do not have zero values, i.e. if we have the snow height of 0, then maintenance takes place in non-zero time, because technique would be idle.[15]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
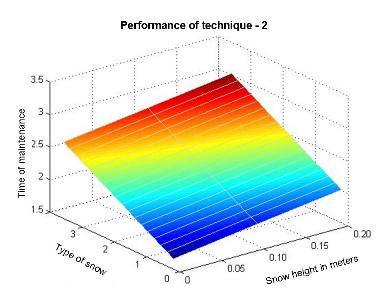 | Figure 6. The graph of the dependence on performance techniques 2 |
5. Conclusions
- Currently, for assessment of the effectiveness of deployment and variation of technical means, information technology can be widely used. The design of optimal set of means of WMA can be solved according to specified input and output for a specific period of such as five years. Then we can compare the actual cost and the solution of proposal of techniques to WMA for the two largest Slovak airports with outputs of a mathematical model of the winter maintenance of the airport.The designed model to optimize the use of technical means of winter maintenance of the airport and to establish the optimal time depends on the capacity of airfields. For the established technique, also envisaged economic benefits, particularly in connection with the setting of input parameters of the airport in increasing density of air traffic, the management of airport can find an optimized set of techniques to airport maintenance and conversely of existing airport maintenance.
References
| [1] | S. N. Kartashov: Physical properties of snow and firn, Institute of Geocryology, Academy of sciences, Siberian department, Russia. Online Available:http://iahs.info/redbooks/a069/069014.pdf |
| [2] | P. Koščák, M. Petruf, M. Lazorik: Analysis winter maintenance of airport, New Trends in Aviation Development, proceedings of the 9th international scientific conference, High Tatras, Slovak Republic. Fakulty of Aeronautics TU Košice, 2010, pp. 89-92. - ISBN 978-80-553-0475-5 |
| [3] | J. Kolesár, P. Koščák: Winter Maintenance of Airport Movement Area, scripts. Vol. 1, Fakulty of Aeronautics TU Košice, Slovak Republic, 2012, 172 p. ISBN 978-80-553-0886-9. |
| [4] | A. Kazda,, R. E Caves: Airport design and operation, Second edition, Elsevier Amsterdam, 2007, ISBN-13: 978-0-08-045104-6, |
| [5] | P. Koščák, M. Lazorik: Maintenance of airports in winter, Acta Avionica. Volume 11, No. 17, 2009, pp. 213-215. - ISSN 1335-9479 |
| [6] | Z. Žihla: Operation of Air Transport and Airports, CERM, Brno, 2010, ISBN 978-80-7204-677-5 |
| [7] | P. Koščák, J. Kolesár, J. Ferenc: Chemical De-icing Agents and Their Use in Winter Maintenance of Airports, Building Materials. Vol. 8, No. 1-2, 2012, pp. 28-32. - ISSN 1336-6041 |
| [8] | ACI EUROPE: Winter Services Yearbook 2008, PPS Publications Ltd, Publications House Bell Street Reigate Surrey, United Kingdom, |
| [9] | P. Koščák, M. Petruf: Ramp Security Management, Internet, competitiveness and organizational security, 8th annual international conference, T. Bata University in Zlín, Czech Republick, 2011 pp. 173-178. ISBN 978-80-7454-012-7 |
| [10] | P. Koščák, J. Kolesár: Equipment for the Operation and Maintenance of Airports, Vol.1, Fakulty of Aeronautics TU Košice, Slovak Republic,2011. 201 p. ISBN 978-80-553-0752-7. |
| [11] | P. Koščák, E. Straková: Aspects affecting winter maintenance of airports, Acta Avionica. Vol. 12, No. 19, 2010, pp. 102-106. - ISSN 1335-9479 |
| [12] | A. Hoffmann: Winter operations at Munich Airport, Vice President, Airport Operations, Munich International Airport, 2009 |
| [13] | E. Šoltés: Regression and Correlation Analysis with Applications, IURA Edition, Bratislava, 2008. ISBN 978-80-8078-163-7 |
| [14] | Ľ. Floreková, M. Benková: Statistical Methods, TU Košice, 2006, ISBN: 80-7099-411-8, |
| [15] | P. Koščák: Optimization Process Recovery of Selected Technical Means Winter Maintenance of Airports. Thesis, Technical university of Košice, 2010. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML