-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2025; 15(2): 43-56
doi:10.5923/j.ijtmp.20251502.03
Received: Aug. 7, 2025; Accepted: Sep. 2, 2025; Published: Oct. 31, 2025

Analysis of Natural Convection along a Vertical Flat Plate with Temperature-Dependent Viscosity and Thermal Conductivity under Heat Conduction and Viscous Dissipation
Md. Al- Amin, Md. Mahmud Alam, Sree Pradip Kumer Sarker
Department of Mathematics, Dhaka University of Engineering and Technology, Gazipur, Bangladesh
Correspondence to: Md. Mahmud Alam, Sree Pradip Kumer Sarker, Department of Mathematics, Dhaka University of Engineering and Technology, Gazipur, Bangladesh.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This study presents a comprehensive analysis of natural convection flow along a vertical flat plate, incorporating the effects of temperature-dependent viscosity and thermal conductivity, with additional consideration of internal heat conduction and viscous dissipation. The governing equations of continuity, momentum, and energy are formulated to include variable thermophysical properties and are solved numerically under appropriate boundary conditions using an implicit Crank–Nicolson finite difference scheme. The influence of variable viscosity and thermal conductivity on the development of thermal boundary layers, velocity profiles, temperature distributions, and local Nusselt number is systematically investigated. Results reveal that neglecting the temperature dependence of viscosity and thermal conductivity may lead to significant inaccuracies in predicting flow behavior and heat transfer performance. The analysis highlights that enhanced thermal conductivity intensifies heat transfer, while increased viscosity variation notably alters velocity gradients near the wall. This investigation contributes to the development of more accurate predictive models for natural convection-driven thermal systems and offers practical insights relevant to thermal management applications such as electronics cooling, energy systems, and passive ventilation technologies. This numerical study can be explored for different mathematical model. This study can be expanded considering Magneto hydrodynamics, for unsteady flows, considering different physics like radiation effects. This analysis can be extended by considering the moving surface.
Keywords: Natural Convection, Dependent viscosity, Thermal Conductivity, Heat Conduction, Viscous Dissipation, Joule Heating
Cite this paper: Md. Al- Amin, Md. Mahmud Alam, Sree Pradip Kumer Sarker, Analysis of Natural Convection along a Vertical Flat Plate with Temperature-Dependent Viscosity and Thermal Conductivity under Heat Conduction and Viscous Dissipation, International Journal of Theoretical and Mathematical Physics, Vol. 15 No. 2, 2025, pp. 43-56. doi: 10.5923/j.ijtmp.20251502.03.
Article Outline
1. Introduction
- Investigating the interplay between key thermophysical properties and convective heat transfer has long been a subject of both academic interest and practical importance in the fields of fluid dynamics and heat transfer. Among these properties, viscosity and thermal conductivity significantly influence fluid behavior and thermal transport characteristics. In recent years, increasing attention has been directed toward understanding how temperature-dependent variations in viscosity and thermal conductivity affect natural convection, particularly in scenarios involving vertical flat plates subjected to Joule heating and internal heat conduction. This study aims to advance that understanding by analyzing the complex coupling between these variable properties and convective phenomena using robust numerical techniques. By incorporating temperature-dependent viscosity and thermal conductivity into the governing equations, and solving them under realistic boundary conditions, this work seeks to reveal the nuanced effects these parameters have on velocity fields, thermal boundary layers, and heat transfer efficiency. Such insights are critical for optimizing the thermal performance of engineering systems where natural convection plays a dominant role, including passive cooling technologies, electronic thermal management, and energy-efficient building design. The subsequent sections of this paper detail the mathematical formulation, numerical solution methodology, and key findings of the investigation. Through this analysis, the study contributes to the broader effort to develop more predictive and application-oriented models for natural convection processes in the presence of variable thermophysical properties. Sarker et al. [1] investigated the Variable viscosity and thermal conductivity's effects on magneto hydrodynamic (MHD) natural convection flow in a vertical flat plate. Alam et al. [2] examined the impact of a vertical flat plate with heat conduction, pressure stress work, and viscous dissipation in natural convection flow. Alim et al. [3] examined the effect of Joule heating on the coupling of conduction with magneto hydrodynamic (MHD) free convection flow from a vertical flat plate. Rahman et al. [4] demonstrated the effects of temperature-dependent thermal conductivity on magneto hydrodynamic (MHD) free convection flow and a vertical flat plate with heat conduction.Alim et al. [5] investigated the combined effects of viscous dissipation and Joule heating on the coupling of conduction and free convection. Molla et al. [6] examined the natural convection laminar flow with temperature-dependent viscosity and thermal conductivity and a vertically wavy surface. Safiqul Islam et al. [7] demonstrated the effects of temperature-dependent thermal conductivity on natural convection flow along a vertical flat plate with heat generation. Kabir et al. [8] examined the effects of viscous dissipation on magneto hydrodynamic (MHD) spontaneous convection flow along a vertical wavy surface. Hossain [9] examines the effects of viscous and Joule heating on magneto hydrodynamic (MHD) free convection flow with varying plate temperature. Soundalgekar et al. [10] investigate the transient free convection on an isothermal flat plate using finite difference analysis. Elbashbeshy et al. [11] analyse a steady free convection flow down a vertical plate with changing viscosity and thermal diffusivity. Kafoussius et al. [12] explore the numerical investigation of the mixed free and forced convective laminar boundary layer flow past a vertical isothermal flat plate with temperature dependent viscosity.Anwar Hossain et al. [13] present the influence of radiation on the free convection flow of fluid with changing viscosity from a porous vertical plate. In the situation of unsteady flow, Seddeek [14] investigates the impact of varying viscosity on a magneto hydrodynamic (MHD) free convection flow past a semi-infinite flat plate with an aligned magnetic field. G. Palani Kwan et al. [15] calculated A numerical investigation on a vertical plate with changing viscosity and heat conductivity. Siattery JC [16] investigated Momentum, energy and mass transfer in continua. Ockendon H, Ockendon JR. [17] investigated Variable viscosity flows in heated and cooled channels. Elbashbeshy EMA, Dimian MF [18] computed the effects of radiation on the flow and heat transfer over a wedge with variable viscosity. Seddeek MA, Abdelmeguid MS. [19] investigated the effects of radiation and thermal diffusivity on heat transfer over a stretching surface with variable heat flux Balamurugan, K. and Karthikeyan, R [20] studied viscous dissipation effect on steady free convection flow past a semi-infinite flat plate in the presence of magnetic field. Borah, G. and Hazarika, G. C. [21] calculated the effects of variable viscosity & thermal conductivity on steady free convection flow along a semi-infinite vertical plate (in presence of uniform transverse magnetic field). Abdel-Rahman, G. M. [22] investigated the effects of variable viscosity and thermal conductivity on unsteady MHD flow of non-Newtonian fluid over a stretching porous sheet. Alam, M. M., Alim, M. A. and Chowdhury, M. M. K. [23] investigated free convection from a vertical permeable circular cone with pressure work and non-uniform surface temperature. Aktar, S., Mahmuda Binte Mostafa Ruma and Alim, M. A. [24] calculated the conjugate effects of heat and mass transfer on natural convection flow along an isothermal sphere with radiation heat loss was. Nasrin, R. and Alim, M. A. [25] studied the MHD free convection flow along a vertical flat plate with thermal conductivity and viscosity depending on temperature. Miraj et al. [26] calculated the effects of viscous dissipation and radiation on natural convection flow on a sphere in presence of heat generation. Haque et al. [27] investigated the effects of viscous dissipation on Natural convection flow over a sphere with temperature dependent thermal conductivity. Gebhart, B. [28] studied the effects of viscous dissipation in natural convection. Based on experimental analysis, an analytical solution for the dependent thermal conductivity and variable viscosity in natural convection flow over a vertical flat plate in the presence of heat conduction will be created in this work. A. Pozzi, and M. Lupo, [29] investigated the coupling of conduction with laminar natural convection along a flat plate. Al-Mahasne Mayas Mohammad et al. [30] calculated the variable Temperature Plate Heat Transfer: MHD Fluid Natural Convection Flow in Porous Medium. Journal of Advanced Research in Numerical Heat Transfer. Iqbal Athal et al. [31] studied the Viscosity dissipation and mixed convection flow in a vertical double-passage channel with permeable fluid. Md. Farhad Hasan et al. [32] calculated the Natural Convection Flow over a Vertical Permeable Circular Cone with Uniform Surface Heat Flux in Temperature-Dependent Viscosity with Three-Fold Solutions within the Boundary Layer. Sujit Mishra et al. [33] studied Thermal performance of nanofluid flow along an isothermal vertical plate with velocity, thermal, and concentration slip boundary conditions employing buongiorno’s revised non-homogeneous model. East European Journal of Physics. Uzma Ahmad et al. [34] investigated the Effects of temperature dependent viscosity and thermal conductivity on natural convection flow along a curved surface in the presence of exothermic catalytic chemical reaction.The governing momentum and energy equations are discretized using central difference approximations for both spatial coordinates in their non-dimensional form. To solve these equations, an implicit finite difference scheme based on the Crank–Nicolson method—recognized for its numerical stability and convergence—has been employed. A custom computational code was developed to simulate the flow and thermal behavior of the system under varying conditions. The analysis yields detailed results for velocity and temperature distributions, local and average skin friction coefficients, and local and average Nusselt numbers across a range of parameters, including temperature-dependent viscosity and thermal conductivity, heat generation, viscous dissipation, Joule heating, and the Prandtl number.By integrating the effects of internal heat conduction and Joule heating into the numerical model, this study offers a comprehensive understanding of the fundamental mechanisms governing complex convective heat transfer processes. The insights derived are particularly relevant for improving predictive modeling in thermal-fluid systems, with practical applications in environmental control, electronic cooling, and renewable energy technologies. Understanding the influence of temperature-dependent fluid properties on natural convection along vertical surfaces is essential for optimizing thermal performance, enhancing energy efficiency, and mitigating thermal management challenges in advanced engineering systems.
2. Mathematical Analysis
- This study addresses the unsteady, laminar flow of a viscous, incompressible fluid along a semi-infinite vertical flat plate. The coordinate system is defined such that the x-axis is aligned vertically upward along the plate surface, while the y-axis extends perpendicularly from the leading edge of the plate, as illustrated in Figure 1. The origin is located at the leading edge of the plate. All thermophysical properties of the fluid are considered constant, except for the density in the buoyancy term of the momentum equation, where the Boussinesq approximation is applied. Additionally, the thermal conductivity is assumed to vary linearly with temperature, while the fluid viscosity exhibits an exponential dependence on temperature. The problem also can be solved improved analytical analysis via perturbation methods for small variations in viscosity and thermal conductivity.
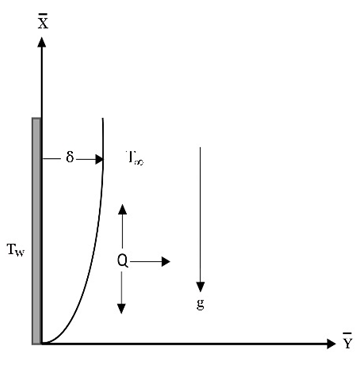 | Figure 1. Geometry |
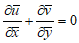 | (1) |
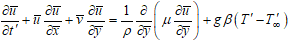 | (2) |
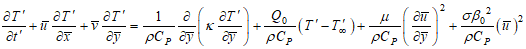 | (3) |
 and
and  are the velocity components along with the
are the velocity components along with the  and
and  axis respectively,
axis respectively,  is the time,
is the time,  is the temperature of the fluid in the boundary layer and
is the temperature of the fluid in the boundary layer and  is the fluid temperature far away from the plate, g is the acceleration due to gravity,
is the fluid temperature far away from the plate, g is the acceleration due to gravity,  is the thermal conductivity of the fluid,
is the thermal conductivity of the fluid,  is the density,
is the density,  is the specific heat at constant pressure and
is the specific heat at constant pressure and  is the variable dynamic co-efficient of viscosity of the fluid. The amount of heat generated or absorbed per unit volume is
is the variable dynamic co-efficient of viscosity of the fluid. The amount of heat generated or absorbed per unit volume is 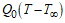 ,
,  being a constant, which may take either positive or negative and the hydrostatic pressure
being a constant, which may take either positive or negative and the hydrostatic pressure 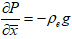 where,
where, 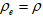 . The source term represents the heat formation when Q0 > 0 and the heat absorption when Q0 < 0.
. The source term represents the heat formation when Q0 > 0 and the heat absorption when Q0 < 0. 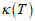 is the thermal conductivity of the fluid depending on the fluid temperature
is the thermal conductivity of the fluid depending on the fluid temperature  ,
,  is the electric conduction and
is the electric conduction and  is the magnetic field strength.The initial and boundary dimensional conditions are
is the magnetic field strength.The initial and boundary dimensional conditions are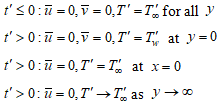 | (4) |
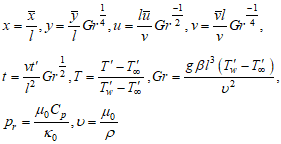 | (5) |
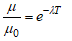 | (6) |
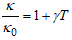 | (7) |
 and
and  denote the viscosity and thermal conductivity variation parameters respectively, depended on the nature of the fluid. Here
denote the viscosity and thermal conductivity variation parameters respectively, depended on the nature of the fluid. Here  and
and  are the viscosity and the thermal conductivity at temperature
are the viscosity and the thermal conductivity at temperature  The equation of continuity is
The equation of continuity is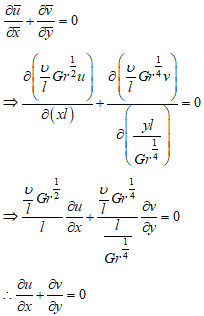 | (8) |
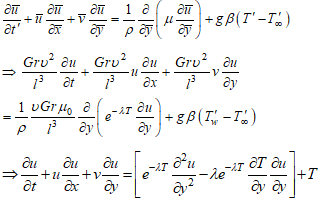 | (9) |
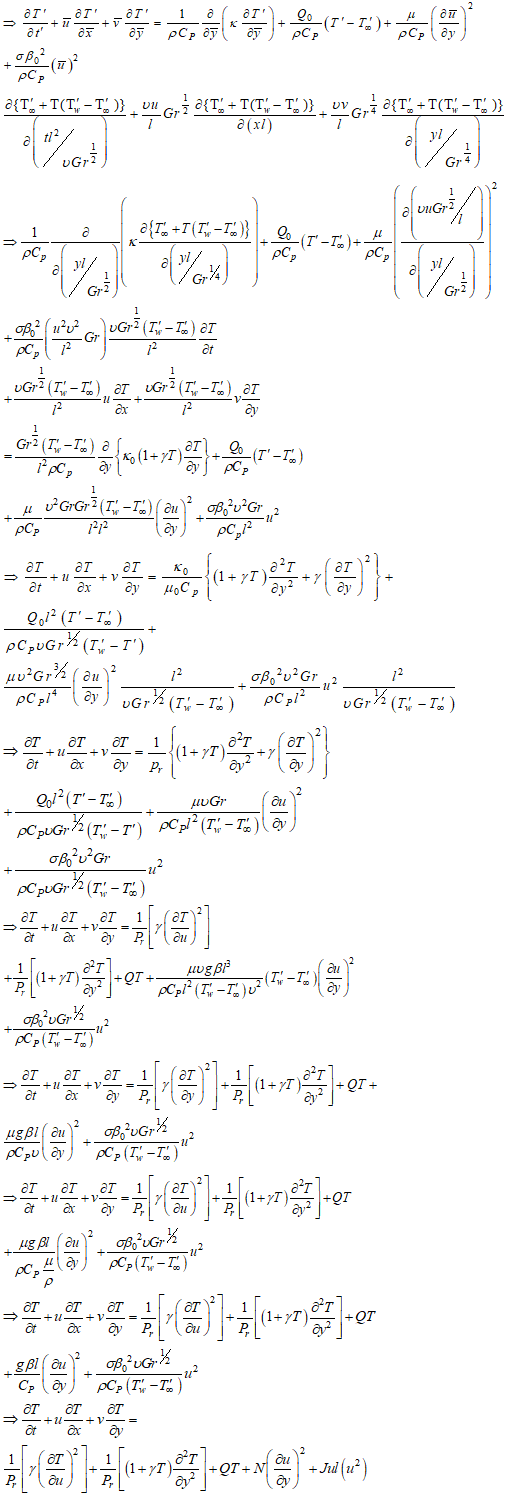 | (10) |
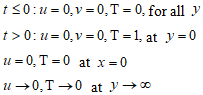 | (11) |
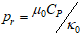 , the Prandtl’s number,
, the Prandtl’s number, 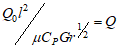 is the heat formation parameter
is the heat formation parameter 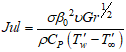 , is the joule heating parameter and
, is the joule heating parameter and 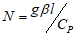 is viscous dissipation parameter.The local shear stress in the plate is defined by
is viscous dissipation parameter.The local shear stress in the plate is defined by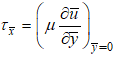 | (12) |
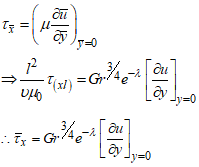 | (13) |
 to gives
to gives  the average skin friction and it is given by
the average skin friction and it is given by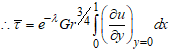 | (14) |
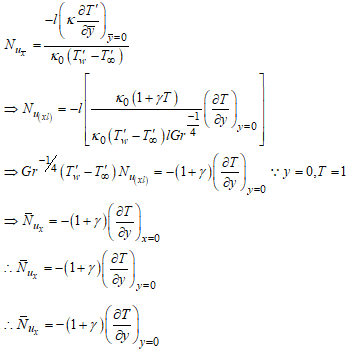 | (15) |
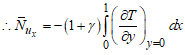 | (16) |
3. Numerical Techniques
- There are many advanced numerical methods like finite difference method, Keller box method, Runge- Kutta shooting method, Spectral collocation method, Finite element method. The two-dimensional, non-linear, unsteady and coupled partial differential “EQ” (8), “EQ” (10) under the initial and boundary conditions in “EQ” (11) are solved using an implicit finite difference scheme of Crank-Nicolson type which is the fast convergent and unconditionally stable. The finite difference equation corresponding to the “EQ” (8) to “EQ” (10) are given by
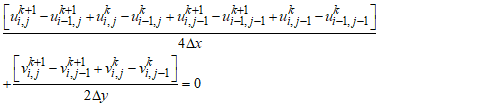 | (17) |
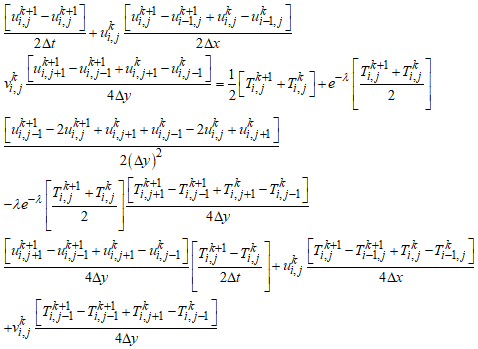 | (18) |
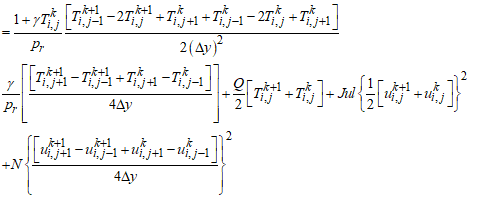 | (19) |
 (=1) and
(=1) and  (=10), where
(=10), where  corresponds to y approaches to ∞. The maximum of y was chosen as 6 after some preliminary investigations so that the last two of the boundary conditions (11) are satisfied. In this case, the grid point along the u-direction is indicated by the subscript i, the v-direction by j, and the t-direction by the superscript k. The coefficients
corresponds to y approaches to ∞. The maximum of y was chosen as 6 after some preliminary investigations so that the last two of the boundary conditions (11) are satisfied. In this case, the grid point along the u-direction is indicated by the subscript i, the v-direction by j, and the t-direction by the superscript k. The coefficients 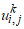 and
and  that appear in the difference equations are treated as constants throughout any one-time step.Because of the beginning conditions, we know the values of u, v, and T at every grid point at t = 0. The following is how the data from the previous time level (fe) are used to calculate u, v, and T at time level (k + 1): The tridiagonal system of equations is made up of the finite difference “EQ” (18) at each internal nodal point on a specific i-level. According to Carnahan et al. [19], the Thomas method solves such a system of equations. For a given i at the (k + l) th time level, the values of T are therefore determined at each nodal point.The values of u at (k + 1) th time level are found similarly to the values of T at (k + 1) th time level in “EQ” (13). Consequently, on a specific i-level, the values of T and u are known. Lastly, at each nodal point on a certain i-level at (k + 1) th time level, the values of v are explicitly determined using the “EQ” (12). For different i-levels, this procedure is repeated. Thus, at the (k + 1) th time level, the values of T, u, and v are known at every grid point in the rectangular region.They have been fixed at the level
that appear in the difference equations are treated as constants throughout any one-time step.Because of the beginning conditions, we know the values of u, v, and T at every grid point at t = 0. The following is how the data from the previous time level (fe) are used to calculate u, v, and T at time level (k + 1): The tridiagonal system of equations is made up of the finite difference “EQ” (18) at each internal nodal point on a specific i-level. According to Carnahan et al. [19], the Thomas method solves such a system of equations. For a given i at the (k + l) th time level, the values of T are therefore determined at each nodal point.The values of u at (k + 1) th time level are found similarly to the values of T at (k + 1) th time level in “EQ” (13). Consequently, on a specific i-level, the values of T and u are known. Lastly, at each nodal point on a certain i-level at (k + 1) th time level, the values of v are explicitly determined using the “EQ” (12). For different i-levels, this procedure is repeated. Thus, at the (k + 1) th time level, the values of T, u, and v are known at every grid point in the rectangular region.They have been fixed at the level  = 0.05,
= 0.05,  = 0.25, and time step
= 0.25, and time step  = 0.01 after a few sets of mesh sizes were taken into consideration. The results are compared after the spatial mesh size is reduced by 50% in one direction and subsequently in both directions. It has been noted that the results vary to the fourth decimal place when the mesh size is decreased by 50% in both the x and y directions. As a result, the sizes listed above have been deemed suitable for calculations.Until the steady-state is achieved, calculations are made. When the absolute difference between the values of u and temperature T at two consecutive time steps is smaller than 10-5 at all grid points, the steady-state solution is said to have been reached.The local truncation error is O (Δf2 + ΔF2 + ΔAx) and it
= 0.01 after a few sets of mesh sizes were taken into consideration. The results are compared after the spatial mesh size is reduced by 50% in one direction and subsequently in both directions. It has been noted that the results vary to the fourth decimal place when the mesh size is decreased by 50% in both the x and y directions. As a result, the sizes listed above have been deemed suitable for calculations.Until the steady-state is achieved, calculations are made. When the absolute difference between the values of u and temperature T at two consecutive time steps is smaller than 10-5 at all grid points, the steady-state solution is said to have been reached.The local truncation error is O (Δf2 + ΔF2 + ΔAx) and it  0 as Δt. Δx and Δy
0 as Δt. Δx and Δy  0, which shows that the scheme is compatible. Additionally, it is demonstrated that the Crank-Nicolson type of implicit finite difference scheme is unconditionally stable for a natural convective flow, where the velocity u and v are always non-negative and non-positive, respectively. Therefore, the implicit finite difference scheme's convergence is guaranteed by compatibility and stability.
0, which shows that the scheme is compatible. Additionally, it is demonstrated that the Crank-Nicolson type of implicit finite difference scheme is unconditionally stable for a natural convective flow, where the velocity u and v are always non-negative and non-positive, respectively. Therefore, the implicit finite difference scheme's convergence is guaranteed by compatibility and stability.4. Results and Discussion
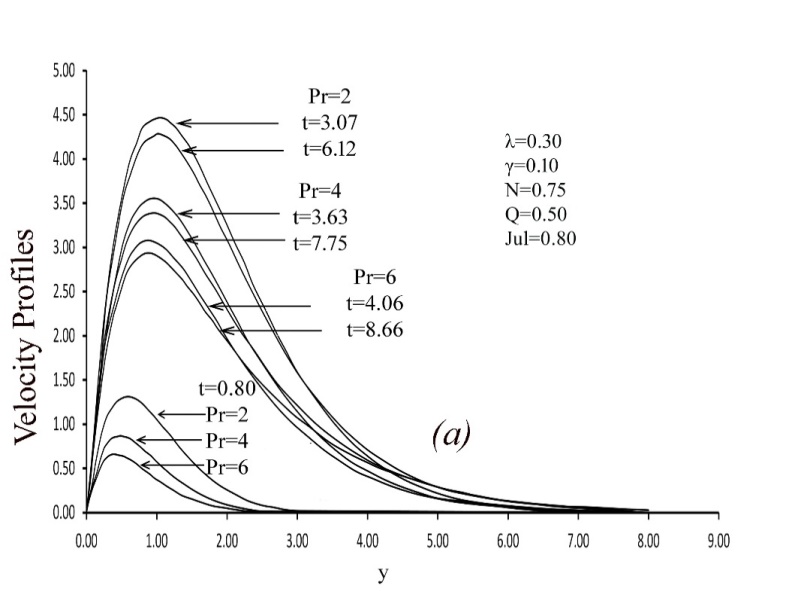
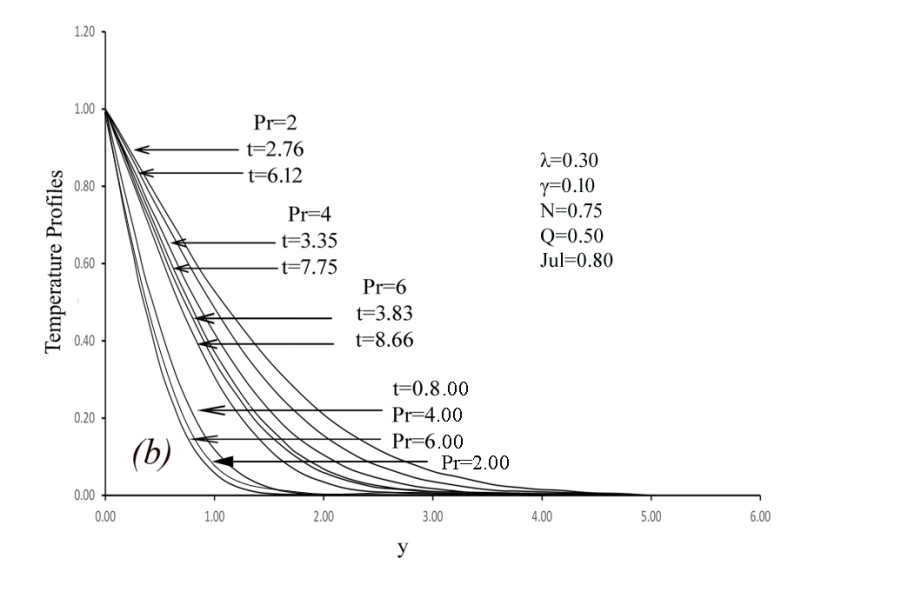
- Heat conduction, also known as thermal diffusion, refers to the microscopic transfer of kinetic energy between particles across a temperature gradient. Among conventional fluids, water is widely used in thermal systems due to its high specific heat capacity and low viscosity, which facilitate efficient heat transport. In certain applications, oil is preferred over water because of its higher boiling point, which enables operation at elevated temperatures without the complications associated with high pressure.Heat transfer mechanisms can generally be categorized into three modes: conduction, convection, and radiation. Convection involves the bulk movement of fluid—such as air or water—carrying thermal energy from one region to another, typically driven by temperature-induced density gradients. For instance, when air is heated, it expands, becomes less dense, and rises, thereby transporting heat through natural convection. Even in fully developed turbulent flows, thermal conduction at the molecular level remains significant, particularly in the near-wall region and within the core of the flow, especially for low-Prandtl-number fluids such as liquid metals.The following ranges for λ, γ and Pr are considered in the present study are:For air: - 0.7 ≤ λ ≤ 0, 0 ≤ γ ≤ 6, Pr = 0.733For water: 0 ≤ λ ≤ 0.6, 0 ≤ γ ≤ 0.12, 2 ≤ Pr ≤ 7.00To assess the precision of our calculated values, we plot the curves calculated by G. palani, Kwang-Yong Kim, and Elbashbeshy & Ibrahim for different values of λ and γ for air (Pr = 0.733) in Figure 2 and Figure 3. Our results show excellent agreement with those of G. palani, Kwang-Yong Kim, and Elbashbeshy & Ibrahim at the steady state.The body force hasn't had enough time to create the proper motion in the fluid during the first phase of the subsequent step changes in the wall temperature. For short times t, the velocity components u and v are therefore insignificant. For constant viscosity and thermal conductivity, pure heat conduction dominates the heat transfer throughout this first transient period. The result of “EQ” (10) is
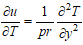 For brief periods, it is seen that the temperature profile depends solely on time and the normal distance from the wall for a given Prandtl's number. Under the beginning and boundary conditions specified in the local Nusellt number, the solutions of “EQ” (15) with Pr = 1 are
For brief periods, it is seen that the temperature profile depends solely on time and the normal distance from the wall for a given Prandtl's number. Under the beginning and boundary conditions specified in the local Nusellt number, the solutions of “EQ” (15) with Pr = 1 are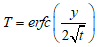 | (20) |
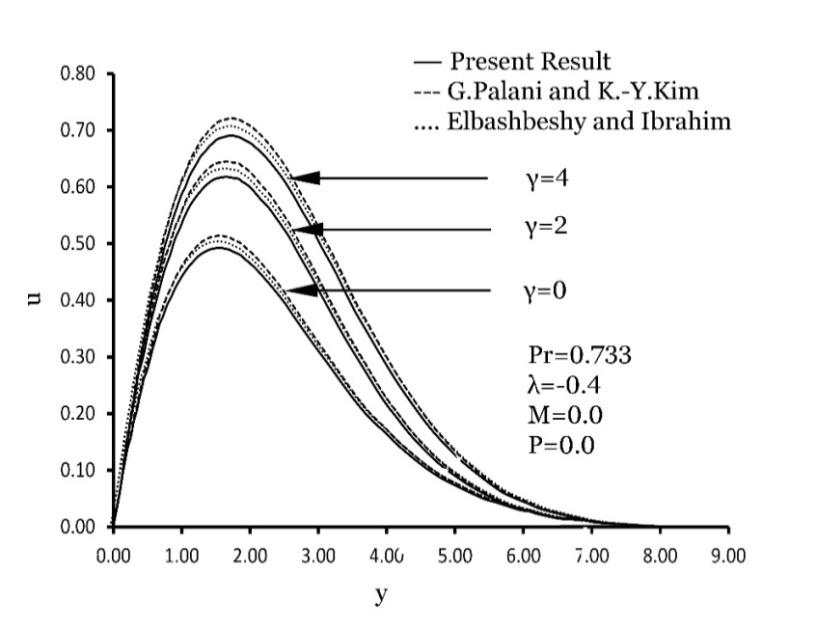 | Figure 2. Comparison of Velocity profiles G. Palani and K.-Y. Kim. Elbashbeshy and Ibrahim for various values |
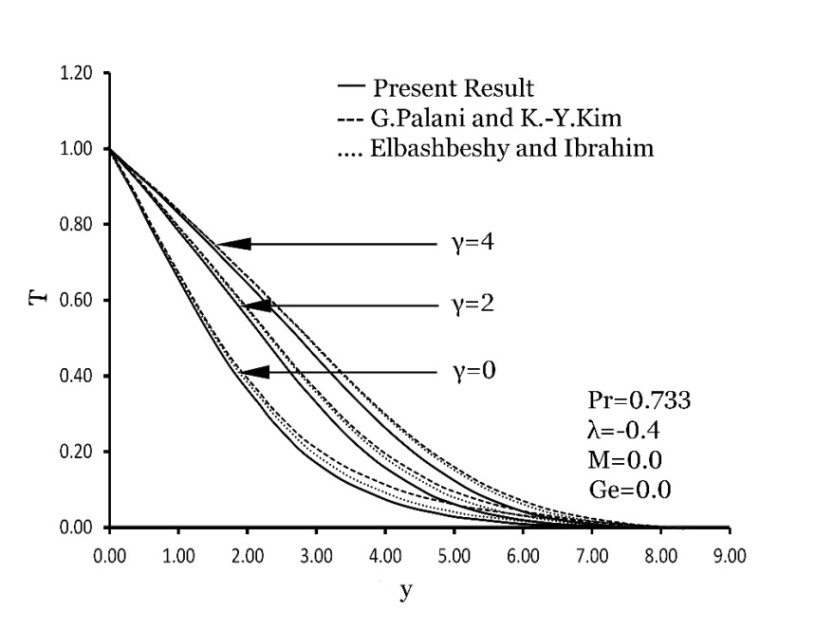 | Figure 3. Comparison of Temperature profiles G. Palani and K.-Y. Kim. Elbashbeshy and Ibrahim for various values |
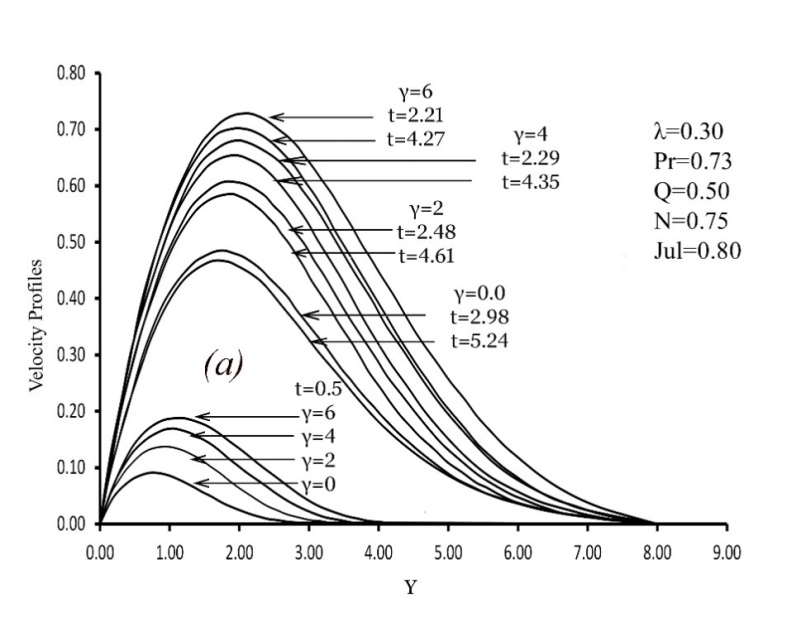
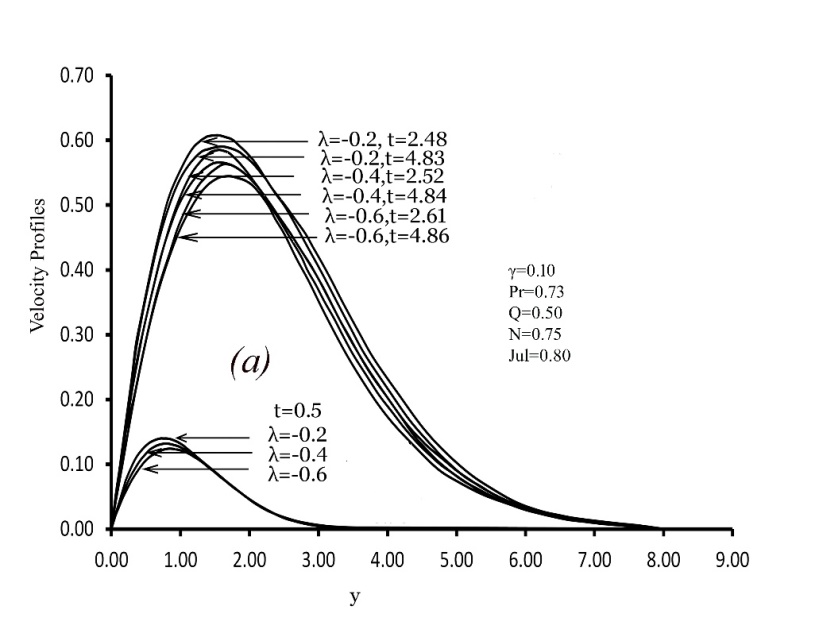 | Figure 4. Variation of dimensionless Velocity profiles versus dimensionless y for various values of viscosity λ and steady state condition with Q=0.5, N=0.75, Jul=0.8, γ =0.1 and Pr= 0.73 |
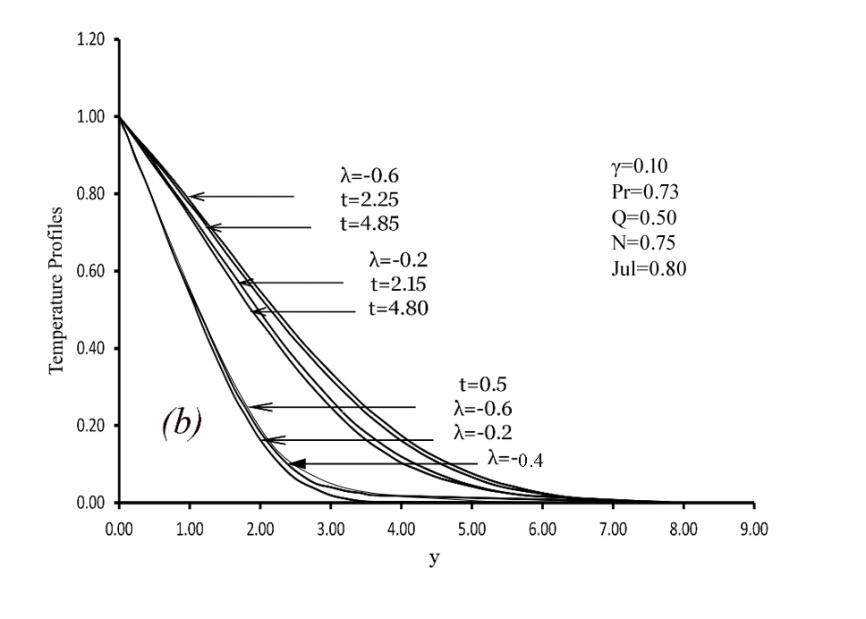 | Figure 5. Variation of dimensionless Temperature profiles versus dimensionless y for various values of viscosity λ and steady state condition with Q=0.5, N=0.75, Jul=0.8, γ =0.1 and Pr= 0.73 |
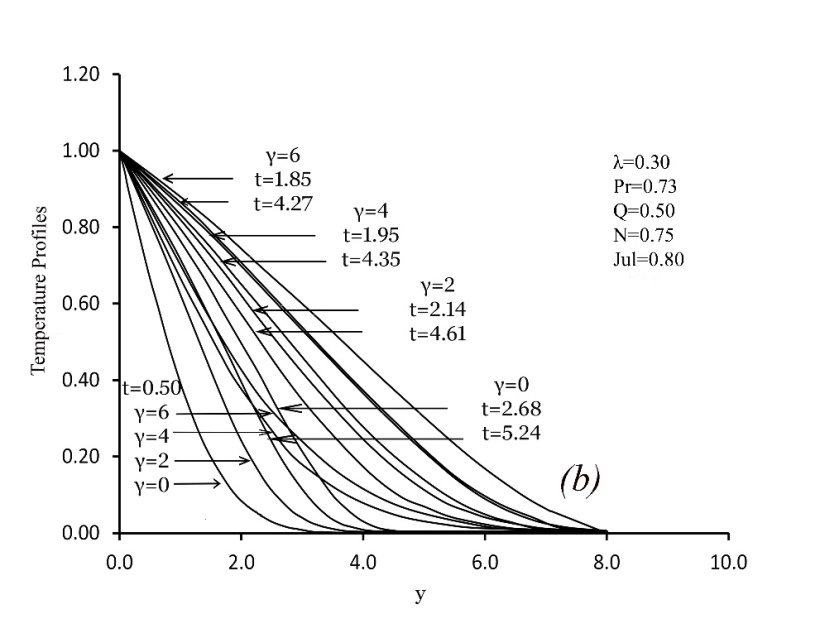
 | Figure 6. Variation of dimensionless Velocity profiles versus dimensionless y for various values of thermal conductivity γ and steady state condition with Q=0.5, N=0.75, Jul=0.8, λ =0.30 and Pr= 0.73 |
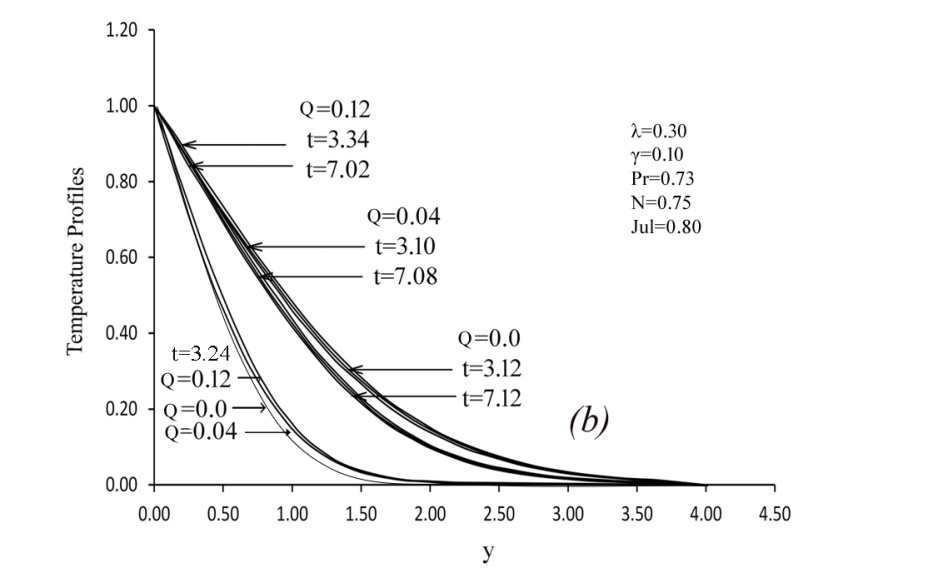
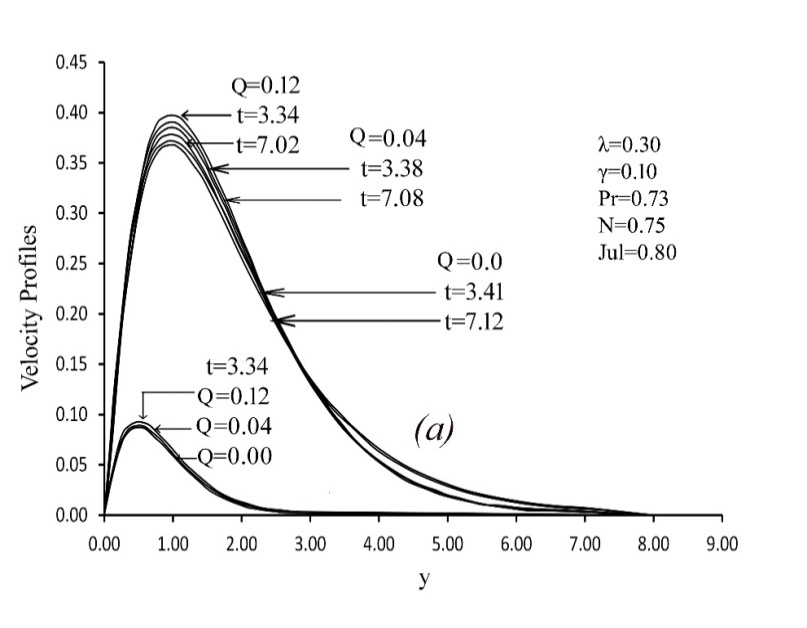 | Figure 10. Variation of dimensionless Velocity profiles versus dimensionless y for different values of heat generation Q and steady state condition with N=0.75, γ =0.10, Jul=0.8, λ =0.30 and Pr= 0.73 |
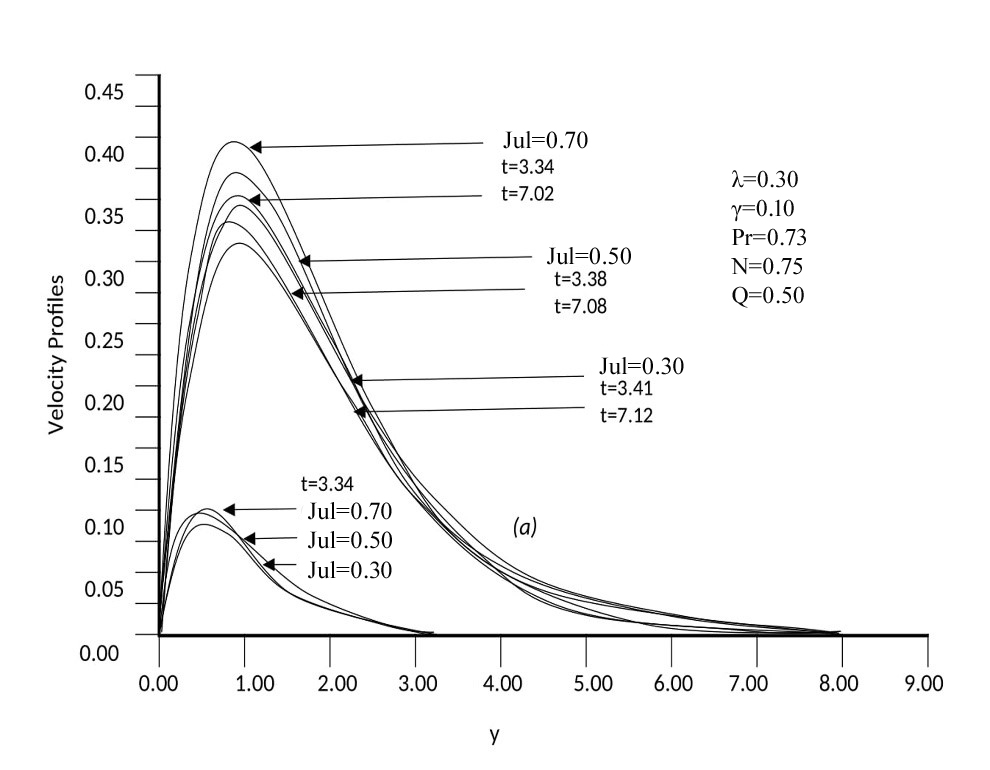 | Figure 12. Variation of dimensionless Velocity profiles versus dimensionless y for different values of Joule and steady state condition with N=0.75, γ =0.10, Q=0.50, λ =0.30 and Pr= 0.73 |
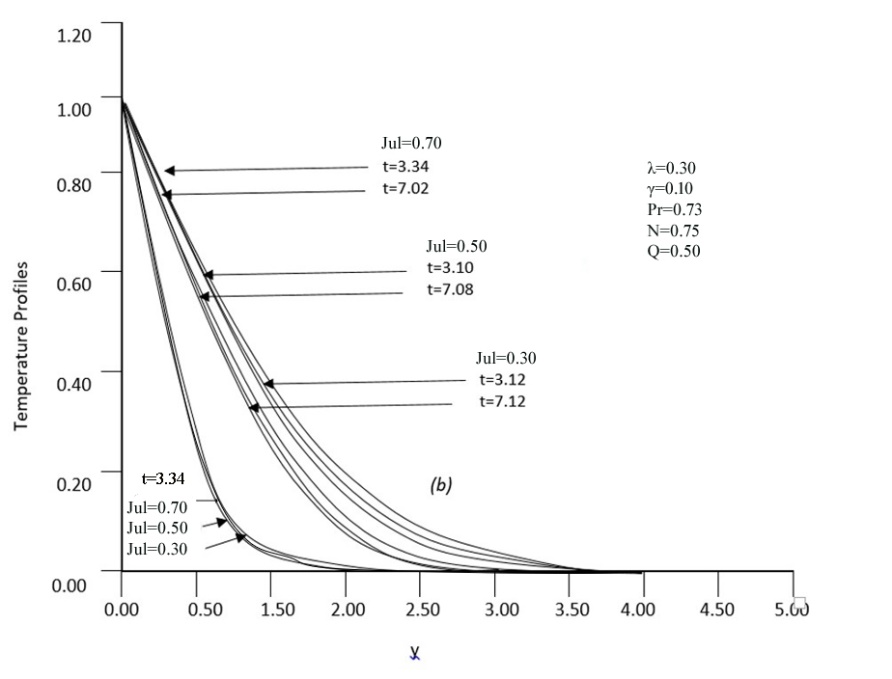 | Figure 13. Variation of dimensionless Temperature profiles versus dimensionless y for different values of Joule and steady state condition with N=0.75, γ =0.10, Q=0.50, λ =0.30 and Pr= 0.73 |
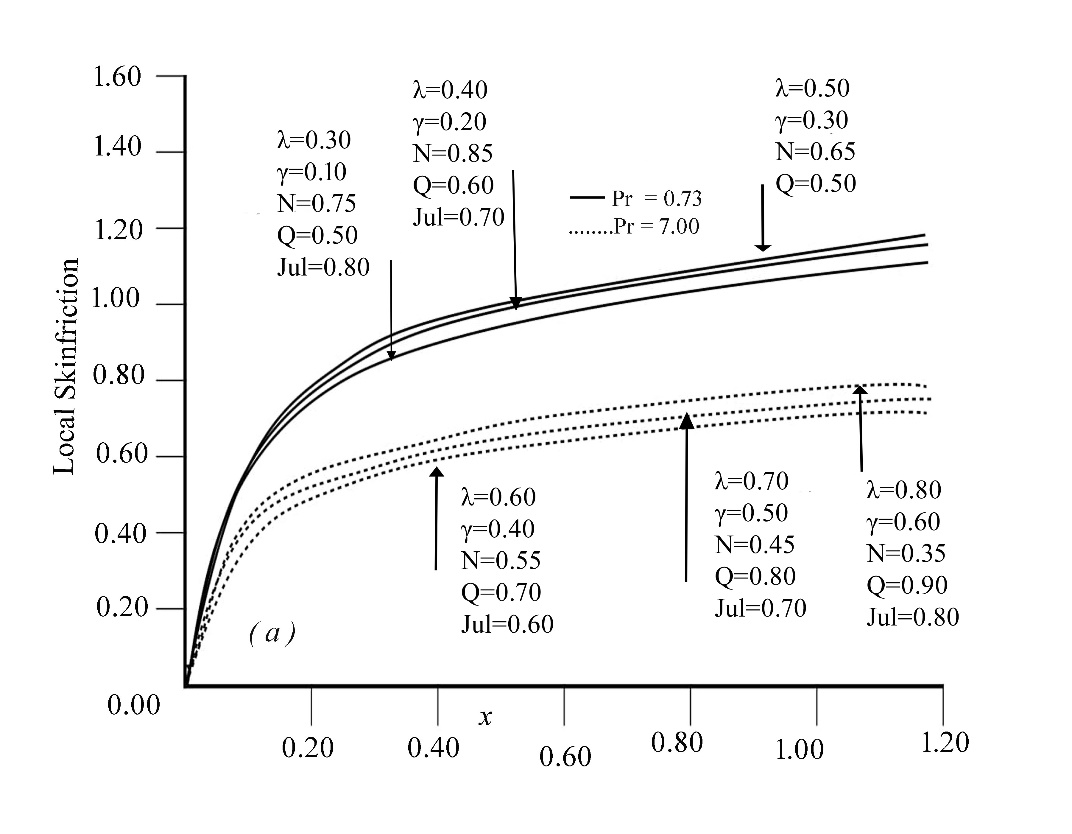 | Figure 16. Variation of dimensionless Local Skin Friction versus dimensionless distance x for different values of Q, λ, γ, N, Jul and Pr at steady state condition |
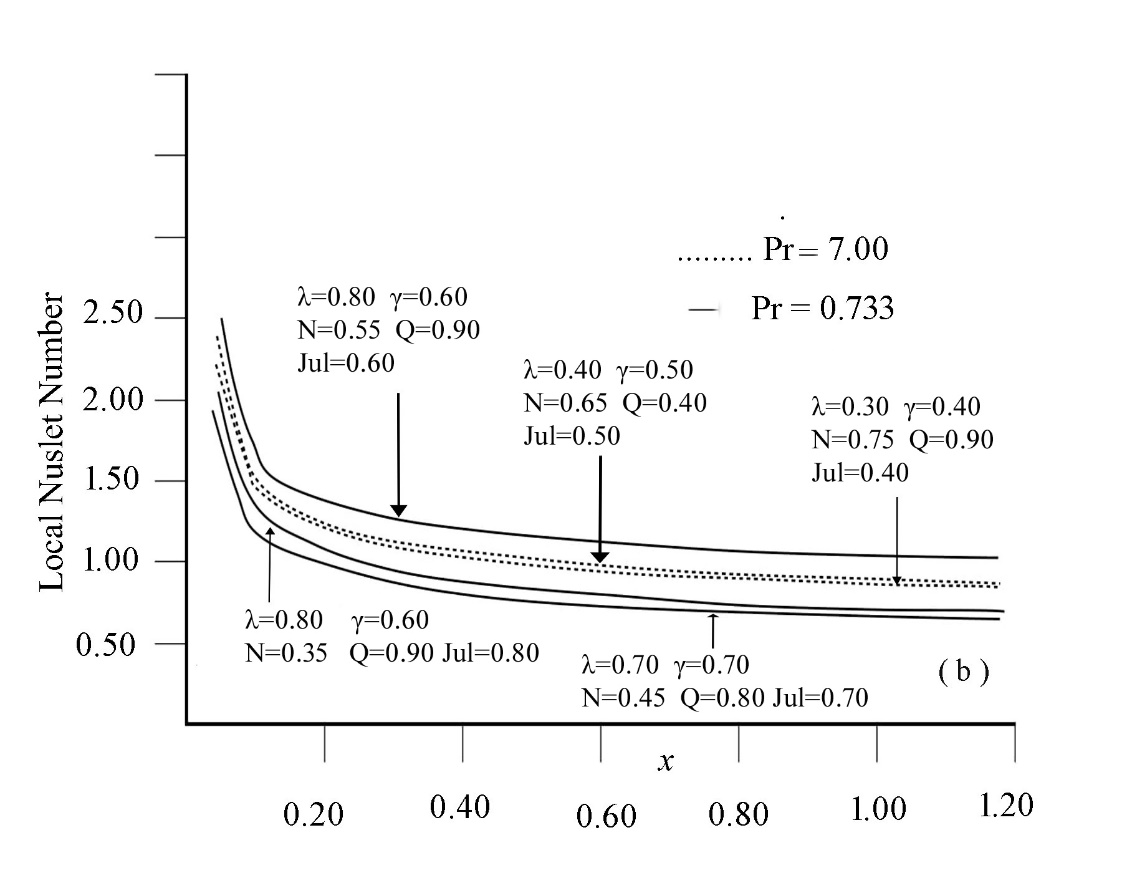 | Figure 17. Variation of dimensionless Local Nusselt number versus dimensionless distance x for different values of Q, λ, γ, N, Jul and Pr at steady state condition |
5. Conclusions
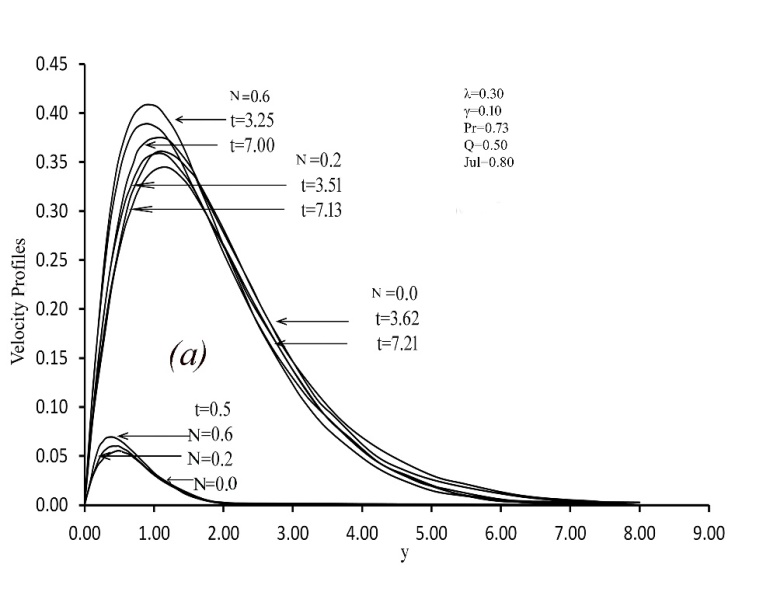
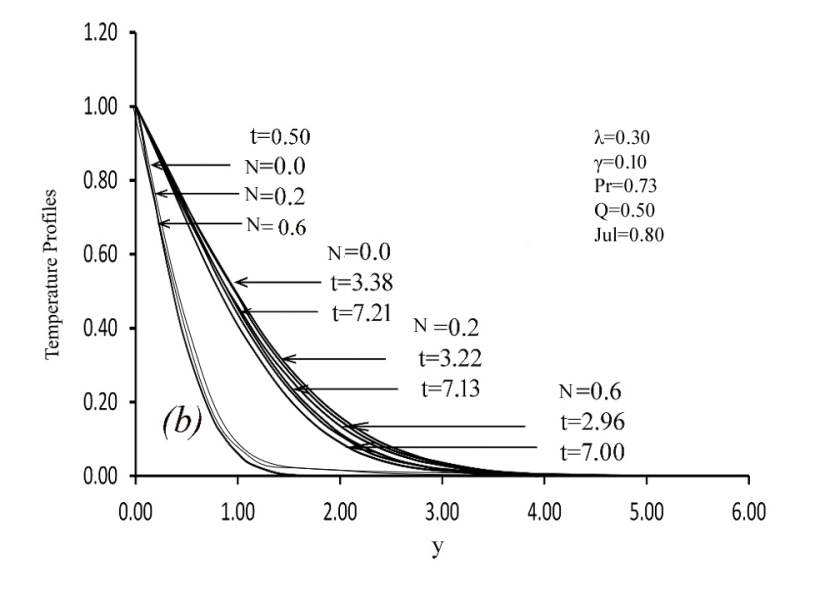
- This study investigates the influence of temperature-dependent viscosity and thermal conductivity on heat generation in laminar natural convection boundary-layer flow along a vertical plate, incorporating the effect of Joule heating, characterized by the parameter Jul. The fluid viscosity is modeled as an exponential function of temperature, while thermal conductivity is assumed to vary linearly with temperature. The dimensionless governing equations are discretized and solved using an implicit Crank–Nicolson finite difference scheme. Numerical results are validated through graphical comparison with previously published studies, demonstrating excellent agreement and confirming the accuracy of the computational approach. The analysis reveals the following key findings:i. Effect of Viscosity Variation: An increase in the viscosity variation parameter enhances the dimensionless velocity near the wall, particularly at lower fluid temperatures. This behavior leads to a higher local Nusselt number and reduced skin friction, indicating improved heat transfer performance.ii. Effect of Thermal Conductivity Variation: As the thermal conductivity parameter increases, both the fluid temperature and velocity rise. Additionally, the wall velocity gradient and the dimensionless heat transfer rate (Nusselt number) are significantly enhanced, indicating stronger convective transport.iii. Importance of Variable Properties: Neglecting the temperature dependency of viscosity and thermal conductivity introduces substantial errors in predicting flow and thermal fields. Accurate modeling of these variations is essential for reliable simulation of natural convection phenomena.iv. Influence of Joule Heating and Heat Generation: Increasing the Joule heating parameter Jul slightly enhances both velocity and temperature profiles. A rise in the internal heat generation parameter Q significantly increases fluid velocity and temperature throughout the boundary layer.v. Combined Effects on Flow and Heat Transfer: Simultaneous variation of Q, the pressure work parameter, and temperature-dependent viscosity and thermal conductivity leads to a decrease in the local skin friction coefficient, local Nusselt number, and velocity across the boundary layer, while the temperature field exhibits a noticeable increase.vi. Effect of Heat Generation Parameter Alone: An isolated increase in Q produces a marked rise in both velocity and temperature profiles, intensifying the convective transport mechanism.vii. Cumulative Parameter Influence: When all key parameters Q, Jul, variable viscosity, and thermal conductivity—are varied together, the trend shows a general decrease in local skin friction and Nusselt number, with a concurrent rise in fluid temperature, emphasizing the dominance of thermal effects over momentum diffusion.Future studies may include the effects of magnetic fields (MHD), use of Nano fluids or hybrid Nano fluids, and extension to three-dimensional or transient models. Investigating variable surface conditions, porous media, and advanced numerical or optimization techniques could further enhance accuracy. Experimental validation is also recommended to support the numerical findings.
Conflicts of Interest
- The authors declare no conflicts of interest.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML