Daddy Balondo Iyela1, 2, Lourenco Conde Macuama1, Prosper Lufungula Nkwambiaya1, Didier Kileba Matondo1, Nestor Anzola Kibamba3
1Department of Physics, University of Kinshasa (UNIKIN), Kinshasa XI, Democratic Republic of Congo
2International Chair in Mathematical Physics and Applications (ICMPA–UNESCO Chair), University of Abomey–Calavi, Cotonou, Republic of Benin
3Department of Mathematics, Statistics and Science Computer, University of Kinshasa (UNIKIN), Kinshasa XI, Democratic Republic of Congo
Correspondence to: Daddy Balondo Iyela, Department of Physics, University of Kinshasa (UNIKIN), Kinshasa XI, Democratic Republic of Congo.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This present work is built on references [1,2]. We restarted all analyses conducted previously and utilized a quantization technique based on a deformed version of Heisenberg's algebra. We applied this method to the quantum harmonic oscillator. Finally, we established the squeezed and coherent states associated with the system of the group SU(1,1), as well as the Wigner distribution function.
Keywords:
Quantization
Cite this paper: Daddy Balondo Iyela, Lourenco Conde Macuama, Prosper Lufungula Nkwambiaya, Didier Kileba Matondo, Nestor Anzola Kibamba, Quantization by Deformation  of the Harmonic Oscillator, Squeezed and Coherent States, International Journal of Theoretical and Mathematical Physics, Vol. 15 No. 1, 2025, pp. 4-9. doi: 10.5923/j.ijtmp.20251501.02.
of the Harmonic Oscillator, Squeezed and Coherent States, International Journal of Theoretical and Mathematical Physics, Vol. 15 No. 1, 2025, pp. 4-9. doi: 10.5923/j.ijtmp.20251501.02.
1. Introduction
For several years, scientists have been interested in defining a structure based on Heisenberg’s algebra.The transition from commutative to non-commutative structures is a frontier of physics and mathematics.Many authors have discussed and applied this approach in various contexts.In 1926, Schrodinger introduced the concept of coherent states in his work on the single harmonic oscillator [3,4]. It is important to note that Glauber, Klauder, and Sudarshan, in the 1960s, were pioneers in applying the concept of coherent states to quantum optics. The term "coherent states" was first coined by Glauber during his research on electromagnetic radiation, where he defined these states as the eigenstates of the annihilation operator for the quantum harmonic oscillator. Furthermore, it has been demonstrated that the coherent states of the harmonic oscillator satisfy the minimization of Heisenberg's uncertainty principle. The algebraic method has proven to be beneficial in providing a unified treatment of these states and their interrelationships. This method has also led to the construction of squeezed states and other related states. The elegant and powerful algebraic approach to construction is rooted in the Heisenberg-Weyl algebra, defined by the relations [a, a†] = 1, in relation to the harmonic oscillator.This current work stemmed from earlier findings discussed in Refs. [1,2], where we revisited the analysis and explored the problem concerning deformation. We have established the relationships associated with the structure of our system through a Harmonic approach, allowing us to diagonalize it using an algebraic method. Furthermore, we examined the symmetries pertinent to our system by employing the group algebraic SU(1,1). As we continue our analysis, we aim to verify Heisenberg’s inequality by utilizing linear combinations of position and momentum operators in terms of creation and annihilation operators.The paper is organized as follows. We demonstrate, through an algebraic approach, the connection between the wave functions of exactly solvable potentials. In Section 1, we present the mathematical formulation of the quantum harmonic oscillator. Section 2 includes the calculation of several commutators. In Section 3, we construct the creation and annihilation operators, which facilitate the diagonalization of the quantum Hamiltonian. Section 4 introduces the elements of the SU(1,1) group to generate squeezed states. In Section 5, we explore various representations in position and momentum to establish the wave functions of excited states for both representations. Section 6 is dedicated to building coherent state wave functions and their corresponding Wigner distribution functions. Finally, in Section 7, we draw our conclusions.
2. Quantum Harmonic Oscillator
In this section, we present our system as defined by the Hamiltonian.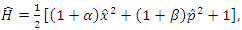 | (1.1) |
where 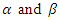 are real parameters. The position and momentum operators obey the commutators as follows
are real parameters. The position and momentum operators obey the commutators as follows 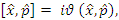 | (1.2) |
where 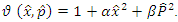 The position and momentum operators are referred to as Hermitian operators and defined as:
The position and momentum operators are referred to as Hermitian operators and defined as: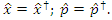 | (1.3) |
3. Construction of the Commutators Relations
We start with the anti-commutator, which can be expressed as follows: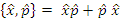 | (1.4) |
We are establishing the commutation relations by examining the position and momentum operators, referencing the deformation relation in Eq. (1.2) as follows: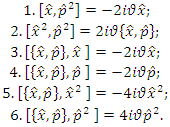 | (1.5) |
4. Diagonalization of the Hamiltonian
a. FOCK states of the systemIn this subsection, we discuss the construction of creation and annihilation operators as linear combinations of position and momentum operators, based on Refs. [5].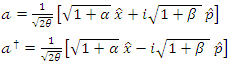 | (1.6) |
From Eq. (1.6ab), we obtain the inverses equations as follows 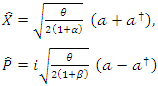 | (1.7) |
Substituting equations (1.7ab) in equation (1.2), we got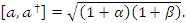 | (1.8) |
Special cases if 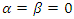 , then the equations above namely (1.1), (1.6ab) and (1.7ab) becomes as follows
, then the equations above namely (1.1), (1.6ab) and (1.7ab) becomes as follows 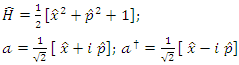 | (1.9) |
Also 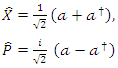 | (1.10) |
Substituting equations (1.6ab) in equation (1.1), we got 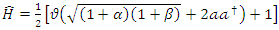 | (1.11) |
If 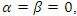 then equation (1.11) reduce as follows
then equation (1.11) reduce as follows 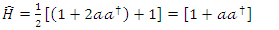 | (1.12) |
From Refs. [5], we draw the notations of algebraic structures as follows 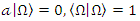 | (1.13) |
In other contexts, we can define a set of orthonormalized states within Hilbert space for the Hamiltonian in the following manner: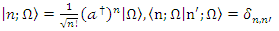 | (1.14) |
where 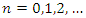 We define the identity operator in the following way:
We define the identity operator in the following way: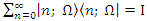 | (1.15) |
This state allows the diagonalisation of the Hamiltonian of the system. We define the projector in the quantum state of the system as follows.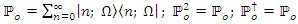 | (1.16) |
We establish the following notation for the remainder of our discussion: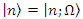 | (1.17) |
Based on the above, the projector of the operators 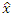 and
and 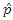 in Hilbert space are
in Hilbert space are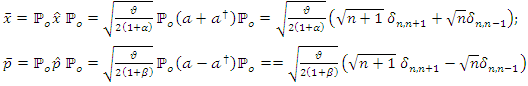 | (1.18) |
The projection of the deformed commutator yields the following results: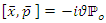 | (1.19) |
This projection of the Heisenberg algebra is deformed across the entire space.b. Energy spectrumWe express the equation for the eigenvalue as follows 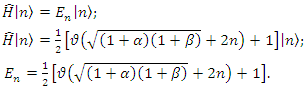 | (1.20) |
If 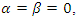 we get the special case where
we get the special case where 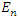 becomes
becomes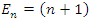 | (1.21) |
We can remark that here, the energy level 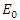 ground state is not zero.
ground state is not zero.
5. Group SU(1,1)
The quantum group SU(1,1) and its associated algebra play a significant role in various quantum physics systems where the formalism of coherent states and squeezing is applied (Refs. [6,7]).The group generators of SU(1,1) are 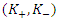 and
and 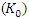 . These generators are defined as follows:
. These generators are defined as follows: | (1.22) |
These group generators SU(1,1) act on the complete base of the FOCK vectors 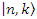 , where
, where 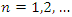 etc. as
etc. as 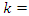
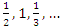 is Bargmann’s index with as representation what follows
is Bargmann’s index with as representation what follows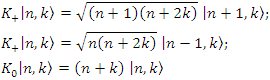 | (1.23) |
In these cases, these three generators 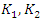 and
and 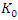 are of the from
are of the from 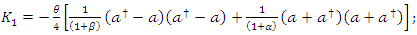 Finally, for
Finally, for 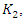 we have
we have 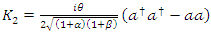 | (1.24) |
Special cases, if 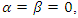 then
then 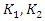 and
and 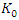 become
become 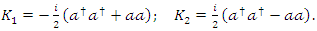 | (1.25) |
We can calculate 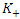 and
and 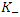 as follows
as follows 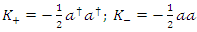 | (1.26) |
we compute 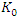 from of the equation (1.22ab) as
from of the equation (1.22ab) as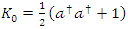 | (1.27) |
From [8,9], knowing 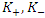 and
and 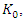 we can establish the commutation relations between then as follows
we can establish the commutation relations between then as follows 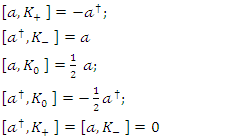 | (1.28) |
The equations (1.7ab) of the squared position and momentum operators as follows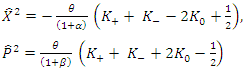 | (1.29) |
The dispersions of the coordinate ant momentum given by 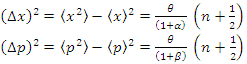 Consequently
Consequently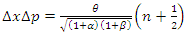 From references [8,9], we introduce the displacement operator of squeezed states for the quantum harmonic oscillator, which is the most complex.Given the unitary squeezed operator as follows
From references [8,9], we introduce the displacement operator of squeezed states for the quantum harmonic oscillator, which is the most complex.Given the unitary squeezed operator as follows 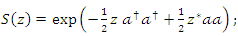 with
with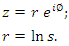 | (1.30) |
Using (1.30ab) in the previous equation, we finally get 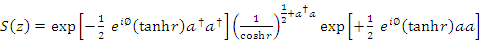 | (1.31) |
We can still rewrite the equation (1.21) in term of the Bargamann indexe 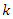 as follows
as follows 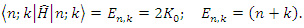 | (1.32) |
Special case, if 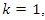 then the equation (1.32b), we got
then the equation (1.32b), we got 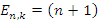 | (1.33) |
6. Position and Momentum Representation
In this section, we build the wave functions under two representations as described in Refs. [10]. Using the creation and annihilation operators, we can define the position and momentum operators as follows: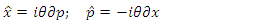 | (1.34) |
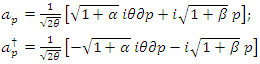 | (1.35) |
From of the equation (1.34a), we built a weve function as follows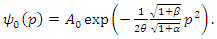 | (1.36) |
Where 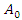 is normalization constant.According to Refs. [11,12,13], the orthogonality properties in the two representations in position and momentum are given by
is normalization constant.According to Refs. [11,12,13], the orthogonality properties in the two representations in position and momentum are given by 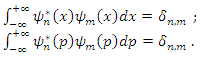 | (1.37) |
After performing the calculations and simplifications, the result for 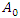 is as follows
is as follows 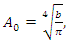 | (1.38) |
where 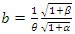 Substituting equations (1.38) in equation (1.36), we got
Substituting equations (1.38) in equation (1.36), we got 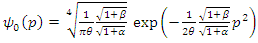 By analogy, we got a wave function in the position representation as follows
By analogy, we got a wave function in the position representation as follows 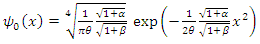 | (1.39) |
In the following discussion, we will consider 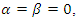 to simplify equations (1.39ab) be easy, as follows:
to simplify equations (1.39ab) be easy, as follows: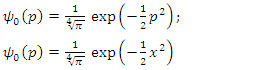 | (1.40) |
We are going to build the excited state as follows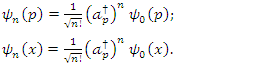 | (1.41) |
We got the two functions in terms position and momentum representations 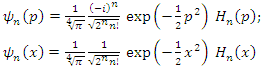 | (1.42) |
7. Quantum Coherent States and Wigner Distributions Functions
a. Quantum coherent states We start by exploring the fundamental relationships of canonical coherent states, as discussed in references [12,13,14,15,16]. These quantum states are defined for all complex numbers Z. We can express a linear superposition of the energy eigenstates in the following manner.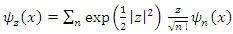 | (1.43) |
Substituting the equation (1.42b) in equation (1.43), we got 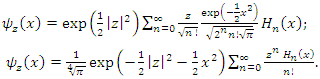 | (1.44) |
We know that 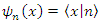 | (1.45) |
We recall the formula for the generating function of Hermite polynomials as follows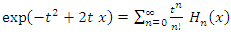 | (1.46) |
Given equation (1.46), equation (1.44b) becomes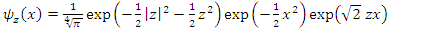 | (1.47) |
By analogy, 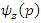 can write as coherent states function writes as follows
can write as coherent states function writes as follows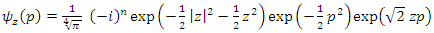 | (1.48) |
b. Wigner distribution function We present the Wigner function as an alternative to the Schrödinger image for addressing quantum mechanical problems, as noted in Refs. [11,12]. Let us recall the Wigner function for the stationary states of a quantum system, denoted as 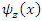 and
and 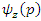 , which are defined by the following relationship:
, which are defined by the following relationship: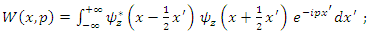 Also
Also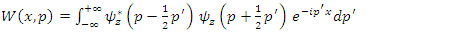 | (1.49) |
By substitution of the equation (1.47) and (1.48) in equations (1.49ab), we get these results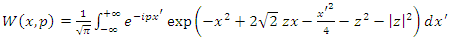 | (1.50) |
According to Refs. [7,12,13], we have the Gaussian integral of the form 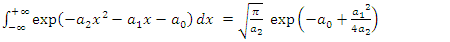 | (1.51) |
Where 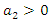 and
and 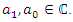 Given the equation (1.51), equation (1.40) becomes
Given the equation (1.51), equation (1.40) becomes 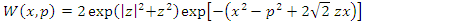 | (1.52) |
By analogy, in the momentum representation, the Wigner function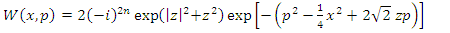 | (1.53) |
8. Conclusions
Our work involved replicating all analyses conducted in Refs. [1,2] while also exploring new directions that are not addressed here. We employed the technique of quantization by deformation, utilizing the deformed Heisenberg algebra to construct the creation and annihilation operators and to determine the physical spectrum of this system. Subsequently, we established the generators of the SU(1,1) group to derive the squeezed states. Building on this foundation, we used the definition of linear superpositions of energy eigenstates to establish the wave functions of coherent states in both position and momentum representations. Finally, we presented the Wigner functions, beginning with a review of the mathematical formulas for the Wigner distribution functions to construct them in the position and momentum frameworks.We provided three illustrative examples of non-Hermitian systems within the domain of quantum mechanics, noting that all these Hamiltonians exhibit a real energy spectrum. This demonstrates that our approach is straightforward and yields reliable results. In our analysis, we observed that among these three examples, only the second one features an energy spectrum that is scaled by a complex phase. This indicates that it is not always evident for two distinct systems governed by different Hamiltonians to share the same equation of motion or energy spectrum.Additionally, we presented a general form of the Hamiltonian that generates these examples. We introduced a local similarity transformation which establishes a connection between the spectra of two related Hamiltonians. This general Hamiltonian can be addressed through an algebraic method, specifically bi-Fock algebras. These bi-Fock algebras enable us to diagonalize the general form of the Hamiltonian and ascertain their physical spectra, which are real.
References
| [1] | M. N. Hounkonnou, D. Ousmane Samary, E. Baloïtcha and S. Arjika:  , deformation of the Harmonic oscillator in a 2D-phase space: [arXiv: 211.0308]. , deformation of the Harmonic oscillator in a 2D-phase space: [arXiv: 211.0308]. |
| [2] | Jean Pierre Atoine: Coherent states and Wavelets, a contemporary panorama: https://dial.uclouvain.be. |
| [3] | T. Shreecharan, Prasant K. Panigrahi and J. Banerji: Coherent states for exactly solvable potentials: [arXiv: 0309038v1 (quant. Ph)]. |
| [4] | Bruno G. Dacosta, Genilson A. C. Da Silva and Ignacio S. Gomez, oscillator with position-dependent effective mass, arXiv 2106.08467v1 (quant. Ph). |
| [5] | Jan Govaerts, Calvin Matondo Bwayi and Olivier Mattelaer, the Klauder. Daubechies construction of the phase space path integral and the Harmonic oscillator: [arXiv: 0908.0805v1]. |
| [6] | H. A. Kastrup, A New LOOK at the quantum méchanics of the Harmonic oscillator: [arXiv: quant. Ph/0612032v1]. |
| [7] | Dusan Popov, Vjekoslav Sajfert, Jovan P. Setrajcic, and Nicolina Pop; Coherent states Formalism applied to the quantum well Model: doi: 10.1166/qm. 2014. 1137. |
| [8] | Bijan Bagch, Rupamanjari Ghosh and Avinash Khare, A pedestrian introduction to coherent and squeezed states, arXiv: 2004.08829v4 (quant-th). |
| [9] | Bogdan M. Mihalcea, Quasienergy operators and generalised squeezed states for systems of trapped ions, arXiv: 2108.11628v2 (quant-th). |
| [10] | Diego J. Cirilo-Lambardo and Norma G. Sanchez, Coherent states of quantum space-times for black Holes and the Sitter space-time: [arXiv: 2312.06628v1]. |
| [11] | A. Isar, Wigner distribution Function for the Harmonic oscillator with dissipation within the Theory of open quatum systems: [arXiv: hep. Th/9310065v1]. |
| [12] | E. I. Jafarov, S. Lievens, S. M. Nagiyev and J. Van der Jeugt, The Wigner function of a q-deformed harmonic oscillator model: [arXiv: math-ph/0702082v2]. |
| [13] | E. I. Jafarov, A. M. Jafarova and S. M. Nagiyev, The Husimi function of a semi confined harmonic oscillator model with a position-dependent effective mass: [arXiv: 2204.02039v2]. |
| [14] | C. L. Ching, C. X. Yeo and W. K. Mg; Non-relativistic Anti-snyder Model end Some Applications: [arXiv: 1601.04420v1]. |
| [15] | Stjepan Meljanac and Salvatore Mignemi; Quantum Mechanics of the Extended Snyder Model: https://doi.org/10.3390/sym15071373. |
| [16] | Jan Mostowski and Joanna Pietraszewicz; Winger Function for Harmonic oscillator and the classical limit: [arXiv: 2104.06638v1]. |

 of the Harmonic Oscillator, Squeezed and Coherent States
of the Harmonic Oscillator, Squeezed and Coherent States

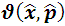 of the Harmonic Oscillator, Squeezed and Coherent States, International Journal of Theoretical and Mathematical Physics, Vol. 15 No. 1, 2025, pp. 4-9. doi: 10.5923/j.ijtmp.20251501.02.
of the Harmonic Oscillator, Squeezed and Coherent States, International Journal of Theoretical and Mathematical Physics, Vol. 15 No. 1, 2025, pp. 4-9. doi: 10.5923/j.ijtmp.20251501.02.
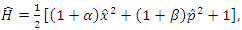
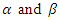 are real parameters. The position and momentum operators obey the commutators as follows
are real parameters. The position and momentum operators obey the commutators as follows 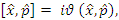
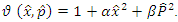 The position and momentum operators are referred to as Hermitian operators and defined as:
The position and momentum operators are referred to as Hermitian operators and defined as: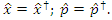
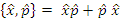
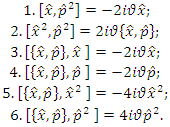
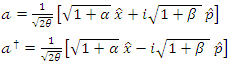
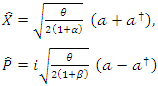
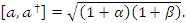
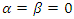 , then the equations above namely (1.1), (1.6ab) and (1.7ab) becomes as follows
, then the equations above namely (1.1), (1.6ab) and (1.7ab) becomes as follows 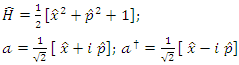
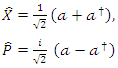
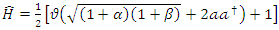
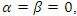 then equation (1.11) reduce as follows
then equation (1.11) reduce as follows 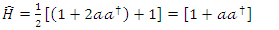
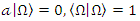
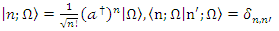
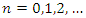 We define the identity operator in the following way:
We define the identity operator in the following way: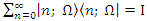
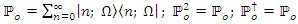
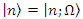
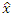 and
and 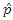 in Hilbert space are
in Hilbert space are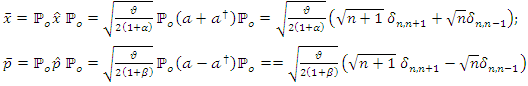
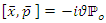
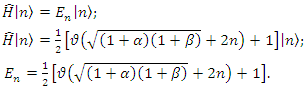
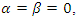 we get the special case where
we get the special case where 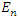 becomes
becomes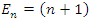
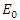 ground state is not zero.
ground state is not zero.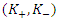 and
and 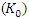 . These generators are defined as follows:
. These generators are defined as follows:
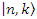 , where
, where 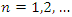 etc. as
etc. as 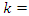
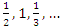 is Bargmann’s index with as representation what follows
is Bargmann’s index with as representation what follows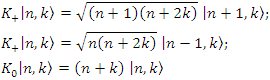
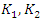 and
and 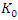 are of the from
are of the from 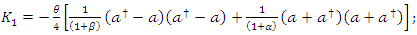 Finally, for
Finally, for 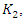 we have
we have 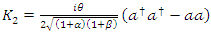
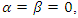 then
then 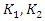 and
and 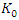 become
become 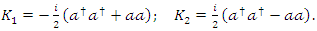
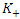 and
and 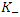 as follows
as follows 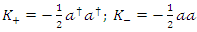
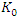 from of the equation (1.22ab) as
from of the equation (1.22ab) as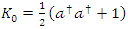
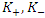 and
and 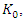 we can establish the commutation relations between then as follows
we can establish the commutation relations between then as follows 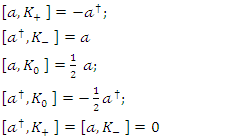
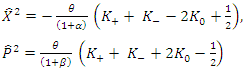
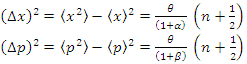 Consequently
Consequently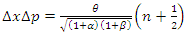 From references [8,9], we introduce the displacement operator of squeezed states for the quantum harmonic oscillator, which is the most complex.Given the unitary squeezed operator as follows
From references [8,9], we introduce the displacement operator of squeezed states for the quantum harmonic oscillator, which is the most complex.Given the unitary squeezed operator as follows 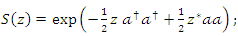 with
with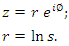
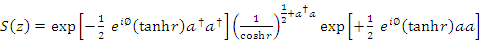
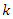 as follows
as follows 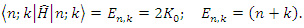
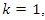 then the equation (1.32b), we got
then the equation (1.32b), we got 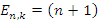
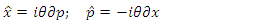
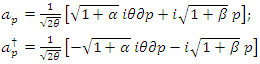
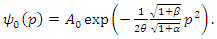
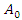 is normalization constant.According to Refs. [11,12,13], the orthogonality properties in the two representations in position and momentum are given by
is normalization constant.According to Refs. [11,12,13], the orthogonality properties in the two representations in position and momentum are given by 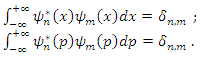
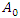 is as follows
is as follows 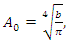
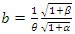 Substituting equations (1.38) in equation (1.36), we got
Substituting equations (1.38) in equation (1.36), we got 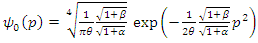 By analogy, we got a wave function in the position representation as follows
By analogy, we got a wave function in the position representation as follows 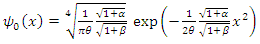
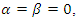 to simplify equations (1.39ab) be easy, as follows:
to simplify equations (1.39ab) be easy, as follows: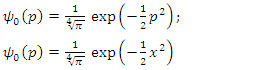
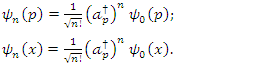
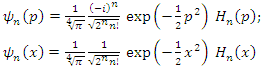
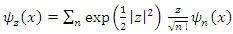
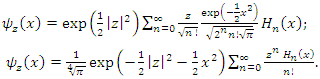
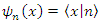
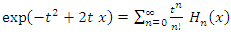
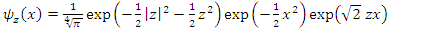
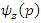 can write as coherent states function writes as follows
can write as coherent states function writes as follows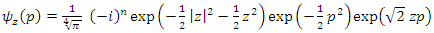
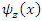 and
and 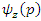 , which are defined by the following relationship:
, which are defined by the following relationship: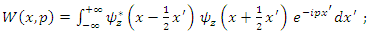 Also
Also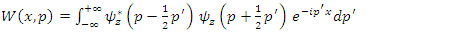
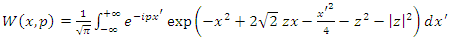
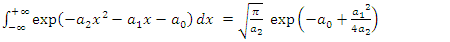
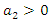 and
and 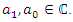 Given the equation (1.51), equation (1.40) becomes
Given the equation (1.51), equation (1.40) becomes 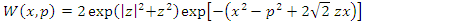
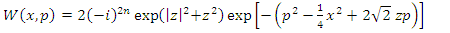
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML , deformation of the Harmonic oscillator in a 2D-phase space: [arXiv: 211.0308].
, deformation of the Harmonic oscillator in a 2D-phase space: [arXiv: 211.0308].