| [1] | Grätzel M. And O’Regan B. (1991). A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films, Nature, 353:737–740. |
| [2] | Duong, T. T., Choi, H. J., He, Q. J., Le, A. T., & Yoon, S. G. (2013). Enhancing the efficiency of dye sensitized solar cells with a SnO2 blocking layer grown by nanocluster deposition. Journal of Alloys and Compounds, 561, 206-210. |
| [3] | Xu, F., Zhang, X., Wu, Y., Wu, D., Gao, Z., & Jiang, K. (2013). Facile synthesis of TiO2 hierarchical microspheres assembled by ultrathin nanosheets for dye-sensitized solar cells. Journal of Alloys and Compounds, 574, 227-232. |
| [4] | Govindaraj R., Senthil M., Ramasamy P. and Mukhopadhyay S. (2014). Synthesis oftitanium dioxide nanostructures and their effects on current-voltage (I-V) performance in dye sensitized solar cells, International Journal of Chem Tech Research, 6:5220-5225. |
| [5] | Grätzel, M. (2003). Dye-sensitized solar cells. Journal of photochemistry and photobiology C: Photochemistry Reviews, 4(2), 145-153. |
| [6] | Huang, J., Yin, Z., & Zheng, Q. (2011). Applications of ZnO in organic and hybrid solar cells. Energy & Environmental Science, 4(10), 3861-3877. |
| [7] | Beek, W. J., Wienk, M. M., & Janssen, R. A. (2006). Hybrid solar cells from regioregularpolythiophene and ZnO nanoparticles. Advanced Functional Materials, 16(8), 1112-1116. |
| [8] | Zhang, Q., Dandeneau, C. S., Zhou, X., & Cao, G. (2009). ZnO nanostructures for dye-sensitized solar cells. Advanced materials, 21(41), 4087-4108. |
| [9] | Lin, C. Y., Lai, Y. H., Chen, H. W., Chen, J. G., Kung, C. W., Vittal, R., & Ho, K. C. Energy Environ. Sci. 4, 3448 (2011). |
| [10] | Lai, T. H., Tsang, S. W., Manders, J. R., Chen, S., & So, F. (2013). Properties of interlayer for organic photovoltaics. Materials Today, 16(11), 424-432. |
| [11] | M.Tan, M. J., Zhong, S., Li, J., Chen, Z., & Chen, W. (2013). Air-stable efficient inverted polymer solar cells using solution-processed nanocrystalline ZnO interfacial layer. ACS applied materials & interfaces, 5(11), 4696-4701. |
| [12] | Look, D. C., Reynolds, D. C., Sizelove, J. R., Jones, R. L., Litton, C. W., Cantwell, G., &Harsch, W. C. (1998). Electrical properties of bulk ZnO. Solid state communications, 105(6), 399-401. |
| [13] | Forro, L., Chauvet, O., Emin, D., Zuppiroli, L., Berger, H., & Levy, F. (1994). High mobility n-type charge carriers in large single crystals of anatase (TiO2). Journal of Applied Physics, 75(1), 633-635. |
| [14] | Wang, Z. L. (2004). Nanostructures of zinc oxide. Materials today, 7(6), 26-33. |
| [15] | Klingshirn, C. (2007). ZnO: material, physics and applications. ChemPhysChem, 8(6), 782-803. |
| [16] | Tributsch, H., & Calvin, M. (1971). Electrochemistry of excited molecules: photo-electrochemical reactions of chlorophylls. Photochemistry and Photobiology, 14(2), 95-112. |
| [17] | Ungula, J. (2015). Growth and characterization of ZnO nanoparticles by sol-gel process (Doctoral dissertation, University of the Free State (Qwaqwa Campus)). |
| [18] | Ungula, J., Dejene, B. F., & Swart, H. C. (2018). Band gap engineering, enhanced morphology and photoluminescence of un-doped, Ga and/or Al-doped ZnO nanoparticles by reflux precipitation method. Journal of Luminescence, 195, 54-60. |
| [19] | Mahmoud, W. E. (2010). Synthesis and optical properties of Ce-doped ZnO hexagonal nanoplatelets. Journal of crystal growth, 312(21), 3075-3079. |
| [20] | Dhamodharan, P., Manoharan, C., Bououdina, M., Venkadachalapathy, R., & Ramalingam, S. (2017). Al-doped ZnO thin films grown onto ITO substrates as photoanode in dye sensitized solar cell. Solar Energy, 141, 127-144. |
| [21] | Kumar, V., Pandey, A., Swami, S. K., Ntwaeaborwa, O. M., Swart, H. C., & Dutta, V. (2018). Synthesis and characterization of Er3+-Yb3+ doped ZnO upconversion nanoparticles for solar cell application. Journal of Alloys and Compounds, 766, 429-435. |
| [22] | Finocchi, F. (2011). Density Functional Theory for Beginners: Basic Principles and Practical Approaches. Institut des NanoSciences de Paris (INSP) CNRS and University Pierre et Marie Curie, Paris. |
| [23] | Zhang, X. J., Mi, W. B., Wang, X. C., & Bai, H. L. (2014). First-principles prediction of electronic structure and magnetic ordering of rare-earth metals doped ZnO. Journal of alloys and compounds, 617, 828-833. |
| [24] | Khuili, M., Fazouan, N., Abou El Makarim, H., El Halani, G., &Atmani, E. H. (2016). Comparative first principles study of ZnO doped with group III elements. Journal of Alloys and Compounds, 688, 368-375. |
| [25] | Haq, B. U., Ahmed, R., &Goumri-Said, S. (2014). DFT characterization of cadmium doped zinc oxide for photovoltaic and solar cell applications. Solar energy materials and solar cells, 130, 6-14. |
| [26] | Ozugurlu, E. (2021). Cd-doped ZnO nanoparticles: an experimental and first-principles DFT studies. Journal of Alloys and Compounds, 861, 158620. |
| [27] | Lee, Y. S., Peng, Y. C., Lu, J. H., Zhu, Y. R., & Wu, H. C. (2014). Electronic and optical properties of Ga-doped ZnO. Thin Solid Films, 570, 464-470. |
| [28] | Qing, X., Zhang, C., Gong, J., & Chen, S. (2021). Ab initio study of photoelectric properties in ZnO transparent conductive oxide. Vacuum, 191, 110391. |
| [29] | Khuili, M., Fazouan, N., Abou El Makarim, H., Atmani, E. H., Rai, D. P., & Houmad, M. (2020). First-principles calculations of rare earth (RE= Tm, Yb, Ce) doped ZnO: Structural, optoelectronic, magnetic, and electrical properties. Vacuum, 181, 109603. |
| [30] | Lei, X., Zhao, G. J., Liang, X. X., & Song, T. L. (2015 January). First-principle Studies of Lattice and Electronic Structure of BexZn1-xO. In Journal of Physics: Conference Series (Vol. 574, No. 1, p. 012049). IOP Publishing. |
| [31] | John, R., & Padmavathi, S. (2016). Ab initio calculations on structural, electronic and optical properties of ZnO in wurtzite phase. Crystal structure theory and applications, 5(02), 24. |
| [32] | Gopal, P., &Spaldin, N. A. (2006). Polarization, piezoelectric constants, and elastic constants of ZnO, MgO, and CdO. Journal of Electronic Materials, 35(4), 538-542. |
| [33] | J.P. Perdew, A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B. 23 (1981) 5048–5079. |
| [34] | Namisi, M. M., Musembi, R. J., Mulwa, W. M., &Aduda, B. O. (2023). DFT study of cubic, tetragonal and trigonal structures of KGeCl3 perovskites for photovoltaic applications. Computational Condensed Matter, 34, e00772. |
| [35] | Allan, L., Mulwa, W. M., Musembi, R. J., &Aduda, B. O. (2022). First Principles Study of the Structural, Mechanical, Electronic, and Lattice Dynamical Properties of the Half-Heusler Alloys ZrCoY (Y= Sb, Bi). arXiv preprint arXiv:2204.03759. |
| [36] | Agapito, L. A., Curtarolo, S., & Nardelli, M. B. (2015). Reformulation of DFT+ U as a pseudohybridhubbard density functional for accelerated materials discovery. Physical Review X, 5(1), 011006. |
| [37] | Friedrich, C., Müller, M. C., & Blügel, S. (2011). Band convergence and linearization error correction of all-electron GW calculations: The extreme case of zinc oxide. Physical Review B, 83(8), 081101. |
| [38] | Zhang, M., Ono, S., Nagatsuka, N., & Ohno, K. (2016). All-electron mixed basis G W calculations of TiO 2 and ZnO crystals. Physical Review B, 93(15), 155116. |
| [39] | Uddin, J., &Scuseria, G. E. (2006). Theoretical study of ZnO phases using a screened hybrid density functional. Physical Review B, 74(24), 245115. |
| [40] | Gerosa, M. (2018). Special issue on self-interaction corrected functionals for solids and surfaces. Journal of Physics: Condensed Matter, 30(23), 230301. |
| [41] | Clark, S. J., Robertson, J., Lany, S., &Zunger, A. (2010). Intrinsic defects in ZnO calculated by screened exchange and hybrid density functionals. Physical Review B, 81(11), 115311. |
| [42] | Tran, F., & Blaha, P. (2009). Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Physical review letters, 102(22), 226401. |
| [43] | Khuili, M., El Hallani, G., Fazouan, N., Abou El Makarim, H., &Atmani, E. H. (2019). First-principles calculation of (Al, Ga) co-doped ZnO. Computational Condensed Matter, 21, e00426. |
| [44] | Mulwa, W. M., Ouma, C. N., Onani, M. O., & Dejene, F. B. (2016). Energetic, electronic and optical properties of lanthanide doped TiO2: An ab initio LDA+ U study. Journal of Solid State Chemistry, 237, 129-137. |
| [45] | Deng, X. Y., Liu, G. H., Jing, X. P., & Tian, G. S. (2014). On-site correlation of p-electron in d10 semiconductor zinc oxide. International Journal of Quantum Chemistry, 114(7), 468-472. |
| [46] | Harun, K., Salleh, N. A., Deghfel, B., Yaakob, M. K., & Mohamad, A. A. (2020). DFT+ U calculations for electronic, structural, and optical properties of ZnO wurtzite structure: A review. Results in Physics, 16, 102829. |
| [47] | S.L. Dudarev, G.A. Botton, S.Y. Savrasov, C.J. Humphreys, A.P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B. 57 (1998) 1505–1509. |
| [48] | Cococcioni, M., & De Gironcoli, S. (2005). Linear response approach to the calculation of the effective interaction parameters in the LDA+ U method. Physical Review B, 71(3), 035105. |
| [49] | Ma, X., Wu, Y., Lv, Y., & Zhu, Y. (2013). Correlation effects on lattice relaxation and electronic structure of ZnO within the GGA+ U formalism. The Journal of Physical Chemistry C, 117(49), 26029-26039. |
| [50] | Huang, G. Y., Wang, C. Y., & Wang, J. T. (2012). Detailed check of the LDA+ U and GGA+ U corrected method for defect calculations in wurtzite ZnO. Computer Physics Communications, 183(8), 1749-1752. |
| [51] | Goh, E. S., Mah, J. W., & Yoon, T. L. (2017). Effects of Hubbard term correction on the structural parameters and electronic properties of wurtzite ZnO. Computational Materials Science, 138, 111-116. |
| [52] | Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., &Wentzcovitch, R. M. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of physics: Condensed matter, 21(39), 395502. |
| [53] | Kohn, W., & Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Physical review, 140(4A), A1133. |
| [54] | Perdew, J. P., Burke, K., & Ernzerhof, M. (1996). Generalized gradient approximation made simple. Physical review letters, 77(18), 3865. |
| [55] | Blöchl, P. E., Jepsen, O., & Andersen, O. K. (1994). Improved tetrahedron method for Brillouin-zone integrations. Physical Review B, 49(23), 16223. |
| [56] | Monkhorst, H. J., & Pack, J. D. (1976). Special points for Brillouin-zone integrations. Physical review B, 13(12), 5188-5192. |
| [57] | Motornyi, O., Raynaud, M., Dal Corso, A., & Vast, N. (2018, December). Simulation of electron energy loss spectra with the turboEELS and thermo_pw codes. In Journal of Physics: Conference Series (Vol. 1136, No. 1, p. 012008). IOP Publishing. |
| [58] | Voigt, W. J. T. L. (1928). A determination of the elastic constants for beta-quartz lehrbuch de kristallphysik. Terubner Leipzig, 40, 2856-2860. |
| [59] | Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A, 65(5), 349. |
| [60] | Thirika A.M., Mulwa W.M., Makau N.W., Bamidele I.A (2022) Ab Initio Study of Structural and Vibrational Properties of Fe2P-Type Materials for Near - Room - Temperature Refrigeration. International Journal of Physics, 2022, Vol. 10, No. 1, 49-58. |
| [61] | Momma, K., & Izumi, F. (2011). VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. Journal of applied crystallography, 44(6), 1272-1276. |
| [62] | Khuili, M., Fazouan, N., Abou El Makarim, H., Atmani, E. H., Rai, D. P., &Houmad, M. (2020). First-principles calculations of rare earth (RE= Tm, Yb, Ce) doped ZnO: Structural, optoelectronic, magnetic, and electrical properties. Vacuum, 181, 109603. |
| [63] | Khuili, M., El Hallani, G., Fazouan, N., Abou El Makarim, H., &Atmani, E. H. (2019). First-principles calculation of (Al, Ga) co-doped ZnO. Computational Condensed Matter, 21, e00426. |
| [64] | Chirchir G.K, Mulwa W.M. Bamidele I.A (2022) Structural, Electronic and Mechanical Properties of Re Doped FeMnP 0.67A0.33 (A=Ga and Ge): A DFT Study. International Journal of Physics, 2022, Vol. 10, No. 1, 70-78. |
| [65] | Sarasamak, K., Limpijumnong, S., & Lambrecht, W. R. (2010). Pressure-dependent elastic constants and sound velocities of wurtzite SiC, GaN, InN, ZnO, and CdSe, and their relation to the high-pressure phase transition: A first-principles study. Physical Review B, 82(3), 035201. |
| [66] | Carlotti, G., Fioretto, D., Socino, G., & Verona, E. (1995). Brillouin scattering determination of the whole set of elastic constants of a single transparent film of hexagonal symmetry. Journal of Physics: Condensed Matter, 7(48), 9147. |
| [67] | Tyuterev, V. G., & Vast, N. (2006). Murnaghan’s equation of state for the electronic ground state energy. Computational materials science, 38(2), 350-353. |
| [68] | Mbilo, M., Manyali, G. S., & Musembi, R. J. (2022). Ab initio study of K3Cu3P2 material for photovoltaic applications. Computational Condensed Matter, 32, e00726. |
| [69] | Sun, J., Wang, H. T., He, J., & Tian, Y. (2005). Ab initio investigations of optical properties of the high-pressure phases of ZnO. Physical Review B, 71(12), 125132. |
| [70] | Azam, S., Irfan, M., Abbas, Z., Rani, M., Saleem, T., Younus, A., & Al-Sehemi, A. G. (2019). DFT study of the electronic and optical properties of ternary chalcogenides AlX2Te4. Materials Research Express, 6(11), 116314. |
| [71] | Vettumperumal, R., S. Kalyanaraman, and R. Thangavel. "Optical constants and near infrared emission of Er doped ZnO sol–gel thin films." Journal of Luminescence 158 (2015): 493-500. |
| [72] | Liu, Y., Hou, Q., Sha, S., & Xu, Z. (2020). Electronic structure, optical and ferromagnetic properties of ZnO co-doped with Ag and Co according to first-principles calculations. Vacuum, 173, 109127. |


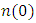 = 1.648 were reported in this study. To investigate on the electronic and elastic properties of W-ZnO, Gopal and Spaldin [32] used the VASP code to implement DFT with Self- Interaction Corrected [33] and LDA potentials for comparison. While the standard LDA underestimated the band gap at 0.78eV, SIC-LDA overestimated it at 3.8eV. The five independent elastic constants for hexagonal W-ZnO obtained with SIC-LDA potentials were C11=217, C12=117, C13=121, C33=225 and C44=50 GPa. From the above discussion, DFT has been verified as a reliable and effective computational technique in the study of fundamental material properties. However, the band gap underestimation in the standard DFT is a major limitation in the accurate prediction of electronic properties of materials. The use of approximated potentials in the Kohn-Sham implementation, results to generation of self-interaction errors [34,35]. The hybridization between the Zn-3d and O-2p shells is therefore inadequately dealt with by standard semi-local exchange correlation (XC) functionals, resulting into the shrinking of the band gap [36]. Several approaches have been proposed to compensate for the band gap underestimation of standard DFT formalism. Green functional (GW) approximation [37,38] puts into consideration the self-energy of a many-body system of electrons and has been used to reproduce the experimental band gaps of semiconductors. On the other hand, hybrid exchange-correlation functionals [39-41] like HSE, PBE0, and B3LYP integrates the GGA exchange potentials with the Hartree–Fock (HF) non-local exact exchange to widen the band gap. Although GW and hybrid potentials have proven to be more accurate than standard DFT, their high computational cost limits their applications. In the recent past, Tran and Blaha modified Becke-Johnson (TB-mBJ) potential have been developed to allow better approximations of band gaps at a reasonable computational cost [42,43]. DFT+U formalism proves to be the most popular remedy to DFT limitationsfor their ease of implementation, low computation cost and high accuracy. DFT+U introduces an on-site Coulombic Hubbard U term [44] into the XC functional of either the LDA or GGA. The magnitude of the on-site potential is basically defined by parameters U (on-site Coulomb) and J (on-site exchange), which can be obtained from first-principle calculations or by comparison with experimental data [45,46]. In the simplistic implementation of DFT+U proposed by [47], the Columbic interaction is included via an effective Ueff (= U−J) parameter as shown in equation (1).
= 1.648 were reported in this study. To investigate on the electronic and elastic properties of W-ZnO, Gopal and Spaldin [32] used the VASP code to implement DFT with Self- Interaction Corrected [33] and LDA potentials for comparison. While the standard LDA underestimated the band gap at 0.78eV, SIC-LDA overestimated it at 3.8eV. The five independent elastic constants for hexagonal W-ZnO obtained with SIC-LDA potentials were C11=217, C12=117, C13=121, C33=225 and C44=50 GPa. From the above discussion, DFT has been verified as a reliable and effective computational technique in the study of fundamental material properties. However, the band gap underestimation in the standard DFT is a major limitation in the accurate prediction of electronic properties of materials. The use of approximated potentials in the Kohn-Sham implementation, results to generation of self-interaction errors [34,35]. The hybridization between the Zn-3d and O-2p shells is therefore inadequately dealt with by standard semi-local exchange correlation (XC) functionals, resulting into the shrinking of the band gap [36]. Several approaches have been proposed to compensate for the band gap underestimation of standard DFT formalism. Green functional (GW) approximation [37,38] puts into consideration the self-energy of a many-body system of electrons and has been used to reproduce the experimental band gaps of semiconductors. On the other hand, hybrid exchange-correlation functionals [39-41] like HSE, PBE0, and B3LYP integrates the GGA exchange potentials with the Hartree–Fock (HF) non-local exact exchange to widen the band gap. Although GW and hybrid potentials have proven to be more accurate than standard DFT, their high computational cost limits their applications. In the recent past, Tran and Blaha modified Becke-Johnson (TB-mBJ) potential have been developed to allow better approximations of band gaps at a reasonable computational cost [42,43]. DFT+U formalism proves to be the most popular remedy to DFT limitationsfor their ease of implementation, low computation cost and high accuracy. DFT+U introduces an on-site Coulombic Hubbard U term [44] into the XC functional of either the LDA or GGA. The magnitude of the on-site potential is basically defined by parameters U (on-site Coulomb) and J (on-site exchange), which can be obtained from first-principle calculations or by comparison with experimental data [45,46]. In the simplistic implementation of DFT+U proposed by [47], the Columbic interaction is included via an effective Ueff (= U−J) parameter as shown in equation (1).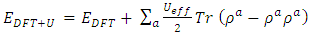
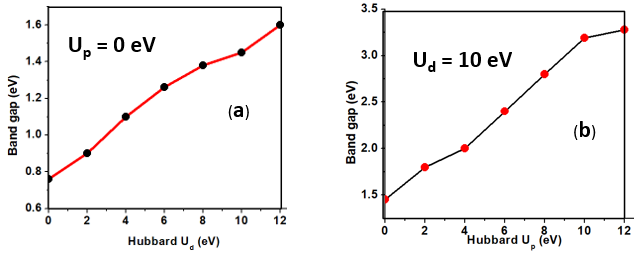
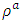 is the atomic orbital matrix. Generally, it is not easy to deduce the optimal value of the coulombic potential U for ZnO. This is after the widely used linear response approach provided by Cococcioni et al. [48] for open-shell systems failed on ZnO since it is a closed-shell system. Dependence of the band gap and lattice parameters of ZnO on the value of Hubbard U has been proposed as a viable route in the determination of the optimal value of U [49]. Huang et al. [50] compared the impact of the Hubbard U term on the structural and electronic aspects of W-ZnO using LDA+U and GGA+U approximation. They introduced the Hubbard U term on both the d orbital of Zn (Ud) as well as the p orbital of oxygen (Up). This method resulted into improved band gap as well as the position of the valence band with GGA+U reporting an improvement of the energy band gap from 0.7 eV to 1.4 eV. Recently, Goh et al. [51] carried out a similar study by applying Hubbard corrections Ud to Zn- 3d states and Up to O-2p states in the LDA+U method. According to this study, while the band gap was enlarged towards experimental value, the lattice constants were underestimated for all the tested Hubbard parameters. So far, the influence of Ud and Up on W-ZnO has largely been focused on structural and electronic properties while their effect on mechanical and optical properties has been greatly ignored. To the best of our knowledge, there exists no report on the optical and mechanical properties of W-ZnO based on the DFT + Ud + Up formalism. Whereas the mechanical properties determines the stability of a compound, optical properties such as dielectric functions, absorption, reflectivity, energy loss and refractive index describes the applicability of a compound in DSSCs. To explore the potential candidature of W-ZnO as a photoanode in DSSCs, this study adopted the DFT + Ud + Up method to investigate the structural, mechanical, electronic and optical properties of W-ZnO.
is the atomic orbital matrix. Generally, it is not easy to deduce the optimal value of the coulombic potential U for ZnO. This is after the widely used linear response approach provided by Cococcioni et al. [48] for open-shell systems failed on ZnO since it is a closed-shell system. Dependence of the band gap and lattice parameters of ZnO on the value of Hubbard U has been proposed as a viable route in the determination of the optimal value of U [49]. Huang et al. [50] compared the impact of the Hubbard U term on the structural and electronic aspects of W-ZnO using LDA+U and GGA+U approximation. They introduced the Hubbard U term on both the d orbital of Zn (Ud) as well as the p orbital of oxygen (Up). This method resulted into improved band gap as well as the position of the valence band with GGA+U reporting an improvement of the energy band gap from 0.7 eV to 1.4 eV. Recently, Goh et al. [51] carried out a similar study by applying Hubbard corrections Ud to Zn- 3d states and Up to O-2p states in the LDA+U method. According to this study, while the band gap was enlarged towards experimental value, the lattice constants were underestimated for all the tested Hubbard parameters. So far, the influence of Ud and Up on W-ZnO has largely been focused on structural and electronic properties while their effect on mechanical and optical properties has been greatly ignored. To the best of our knowledge, there exists no report on the optical and mechanical properties of W-ZnO based on the DFT + Ud + Up formalism. Whereas the mechanical properties determines the stability of a compound, optical properties such as dielectric functions, absorption, reflectivity, energy loss and refractive index describes the applicability of a compound in DSSCs. To explore the potential candidature of W-ZnO as a photoanode in DSSCs, this study adopted the DFT + Ud + Up method to investigate the structural, mechanical, electronic and optical properties of W-ZnO. 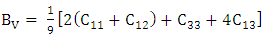
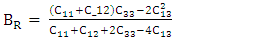

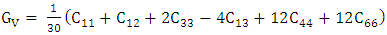
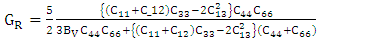


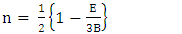

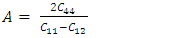
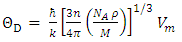
 represents Planck's constant, k denotes Boltzmann's constant, NA signifies Avogadro's number, n indicates the number of atoms per formula unit, M refers to the molecular mass per formula unit, ρ is the density, and Vm is derived from equation 13.
represents Planck's constant, k denotes Boltzmann's constant, NA signifies Avogadro's number, n indicates the number of atoms per formula unit, M refers to the molecular mass per formula unit, ρ is the density, and Vm is derived from equation 13.







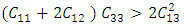
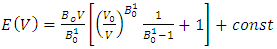


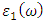 and
and 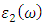 represent the real and imaginary components, respectively, of the complex dielectric function. The real component elucidates the dispersion of photons and the degree of polarization within the material, whereas the imaginary component accounts for the absorption of photons by the material. According to the selection rules, the calculations of the momentum matrix elements between unoccupied and occupied wave functions, as outlined in equation 23, yield the imaginary part
represent the real and imaginary components, respectively, of the complex dielectric function. The real component elucidates the dispersion of photons and the degree of polarization within the material, whereas the imaginary component accounts for the absorption of photons by the material. According to the selection rules, the calculations of the momentum matrix elements between unoccupied and occupied wave functions, as outlined in equation 23, yield the imaginary part 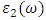 (70)
(70)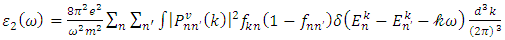
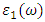 is derived from
is derived from 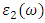 using the Kramer – Kronig relationbelow [71]
using the Kramer – Kronig relationbelow [71]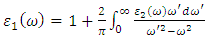
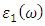 and
and 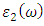 as described in equations 25-28.
as described in equations 25-28.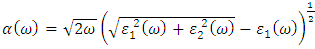
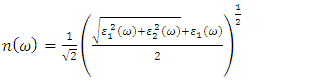


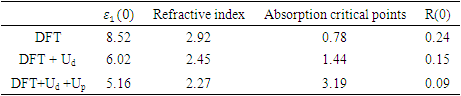
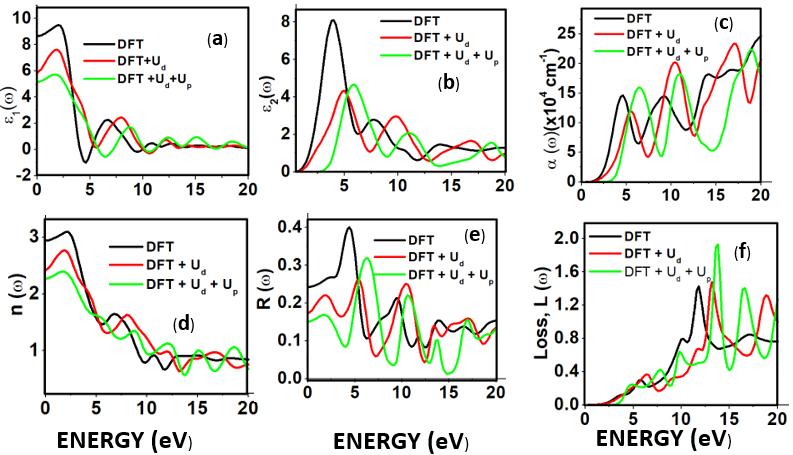
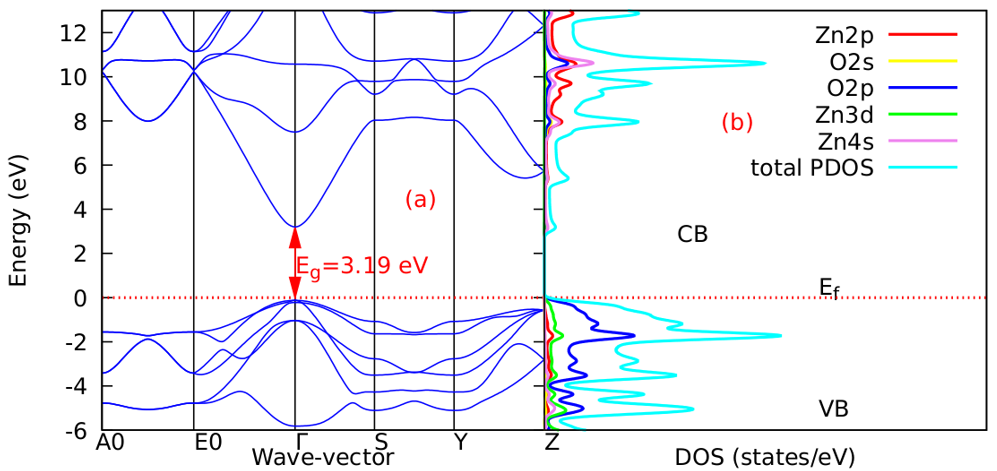
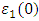 as well as the refractive index. Between 5.1 to 5.8 eV, the curve is negative implying that the radiation is at this point fully attenuated and the ZnO compound behaves like a metal [71]. The imaginary spectrum provides a connection between the optical and electronic band structure of a material. From figure 8(b) of
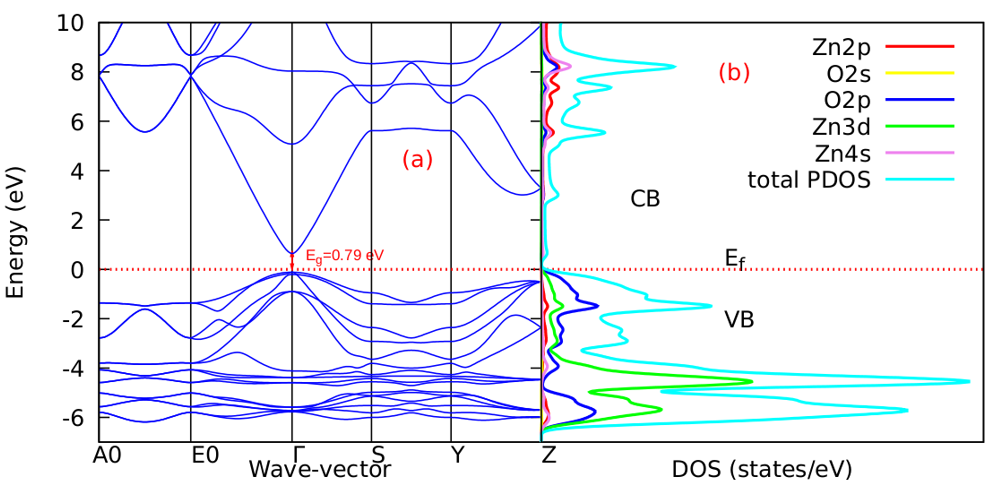
as well as the refractive index. Between 5.1 to 5.8 eV, the curve is negative implying that the radiation is at this point fully attenuated and the ZnO compound behaves like a metal [71]. The imaginary spectrum provides a connection between the optical and electronic band structure of a material. From figure 8(b) of  as a function of energy, the critical onset points are located at 0.78, 1.46and 3.19 eV for DFT, DFT + Ud and DFT+Ud +Up calculations respectively as tabulated in Table 4. The increase in the critical point value from DFT to DFT + Ud to DFT+Ud +Up is collaborative to the results of computed electronic band gaps. The
as a function of energy, the critical onset points are located at 0.78, 1.46and 3.19 eV for DFT, DFT + Ud and DFT+Ud +Up calculations respectively as tabulated in Table 4. The increase in the critical point value from DFT to DFT + Ud to DFT+Ud +Up is collaborative to the results of computed electronic band gaps. The 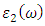 plot exhibited three prominent peaks at energies of 5.12, 10.4, and 13.6 eV, which correspond to the transition of an electron from the valence band to the conduction band. In this context, the transitions of electrons occur between the O-2p and Zn-4s orbitals, the O-2p and Zn-3d orbitals, as well as between the O-2s and Zn-3d orbitals, respectively. The absorption coefficient describes how light intensity diminishes over a specified distance within a material medium. It is greatly affected by the photon frequency implying that the incident photon interacts with material electrons resulting in interband electron transition from the valence to conduction bands. The data presented in Figure 8(c) indicates that the absorption edge of W-ZnO occurs at 0.78 eV, 1.44 eV, and 3.19 eV, corresponding to the DFT, DFT + Ud, and DFT + Ud + Up calculations, respectively. Contrast to standard DFT which predicts absorption of low energy photon including infrared, the DFT+Ud +Up approach reveals that ZnO is transparent to majority of the solar radiation. Consequently, ZnO is able to pass on light to the absorption dye for photoemission and hence current generation [71]. The refractive index, a dimensionless parameter of an optical medium, quantifies the degree to which a light beam is bent when traversing through that medium. [72]. Materials of considerably high (above 1.8) refractive index are desired in photovoltaic applications. The calculated refractive index of W-ZnO is displayed in the plot of Figure 8(d) and the results are presented in Table 4. Despite the reduction of static refractive indices from DFT to DFT + Ud to DFT+Ud +Up, the values are high enough for the application of ZnO as a DSSC photoanode. A substantial drop in the dispersion curve related to the refractive index was observed post the initial peak indicating that beyond a certain amount of photon energy, W-ZnO fails to maintain its transparent nature and instead absorbs such radiations.Reflectivity depicts the surface behavior of a material. Figure 8(e) shows a low reflectivity at zero photon energy (R0). From Table 4, DFT+Ud +Up predicts the least reflectivity of W-ZnO implying the ability of this material to reflect minimum solar radiation but instead allow it to pass through for dye excitation in DSSC. From the plot, the highest peaks are observed at approximately 4.9, 5.1 and 5.8 eV in the DFT, DFT + Ud and DFT+Ud +Up respectively after which the reflectivity rapidly dropped. Energy lossL (ω) is another vital parameter that characterizes the loss of energy of a fast-moving electron as it transverses a material medium. Figure 8(f) shows a near zero energy loss up to 4.0 eV all the approximations techniques. At higher photon energy, the energy loss in ZnO gradually rises to a peak at 12.8, 14.2 and 15.4 eV DFT, DFT + Ud and DFT+Ud +Up respectively. The capability of W-ZnO within UV-Vis region to retain most of its energy with negligible energy loss to the surrounding as desired in DSSCs photoanode is therefore confirmed. However, for high-energy electrons, the energy loss of W-ZnO is relatively high.
plot exhibited three prominent peaks at energies of 5.12, 10.4, and 13.6 eV, which correspond to the transition of an electron from the valence band to the conduction band. In this context, the transitions of electrons occur between the O-2p and Zn-4s orbitals, the O-2p and Zn-3d orbitals, as well as between the O-2s and Zn-3d orbitals, respectively. The absorption coefficient describes how light intensity diminishes over a specified distance within a material medium. It is greatly affected by the photon frequency implying that the incident photon interacts with material electrons resulting in interband electron transition from the valence to conduction bands. The data presented in Figure 8(c) indicates that the absorption edge of W-ZnO occurs at 0.78 eV, 1.44 eV, and 3.19 eV, corresponding to the DFT, DFT + Ud, and DFT + Ud + Up calculations, respectively. Contrast to standard DFT which predicts absorption of low energy photon including infrared, the DFT+Ud +Up approach reveals that ZnO is transparent to majority of the solar radiation. Consequently, ZnO is able to pass on light to the absorption dye for photoemission and hence current generation [71]. The refractive index, a dimensionless parameter of an optical medium, quantifies the degree to which a light beam is bent when traversing through that medium. [72]. Materials of considerably high (above 1.8) refractive index are desired in photovoltaic applications. The calculated refractive index of W-ZnO is displayed in the plot of Figure 8(d) and the results are presented in Table 4. Despite the reduction of static refractive indices from DFT to DFT + Ud to DFT+Ud +Up, the values are high enough for the application of ZnO as a DSSC photoanode. A substantial drop in the dispersion curve related to the refractive index was observed post the initial peak indicating that beyond a certain amount of photon energy, W-ZnO fails to maintain its transparent nature and instead absorbs such radiations.Reflectivity depicts the surface behavior of a material. Figure 8(e) shows a low reflectivity at zero photon energy (R0). From Table 4, DFT+Ud +Up predicts the least reflectivity of W-ZnO implying the ability of this material to reflect minimum solar radiation but instead allow it to pass through for dye excitation in DSSC. From the plot, the highest peaks are observed at approximately 4.9, 5.1 and 5.8 eV in the DFT, DFT + Ud and DFT+Ud +Up respectively after which the reflectivity rapidly dropped. Energy lossL (ω) is another vital parameter that characterizes the loss of energy of a fast-moving electron as it transverses a material medium. Figure 8(f) shows a near zero energy loss up to 4.0 eV all the approximations techniques. At higher photon energy, the energy loss in ZnO gradually rises to a peak at 12.8, 14.2 and 15.4 eV DFT, DFT + Ud and DFT+Ud +Up respectively. The capability of W-ZnO within UV-Vis region to retain most of its energy with negligible energy loss to the surrounding as desired in DSSCs photoanode is therefore confirmed. However, for high-energy electrons, the energy loss of W-ZnO is relatively high. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML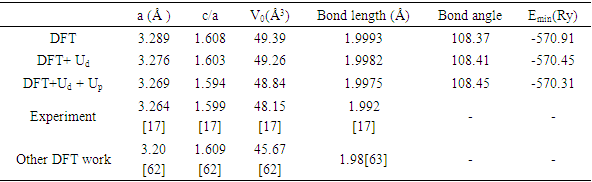
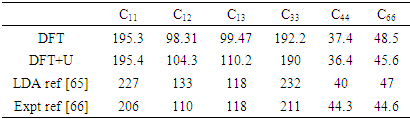
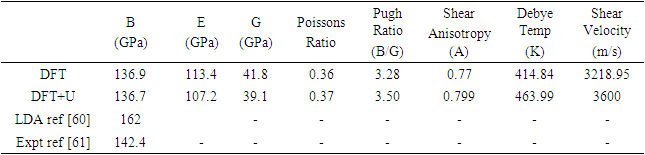
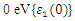 , refractive index (n), absorption critical points and reflectivity at 0 eV (R0)
, refractive index (n), absorption critical points and reflectivity at 0 eV (R0)