-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Theoretical and Mathematical Physics
p-ISSN: 2167-6844 e-ISSN: 2167-6852
2024; 14(3): 70-101
doi:10.5923/j.ijtmp.20241403.02
Received: Jul. 27, 2024; Accepted: Aug. 15, 2024; Published: Aug. 17, 2024

Conservation of Energy and Faraday Tensor in Transformation of Electromagnetic Fields, Maxwell’s Equations, and Symmetric Electromagnetic Field Energy-Momentum Tensor in Theory of Lorentz Invariant Relativistic Electrodynamics
Hilmi Ünlü
Fatih Sultan Mehmet Waqf University, Faculty of Engineering, Department of Electrical and Electronics Engineering, Topkapı, İstanbul, Turkey
Correspondence to: Hilmi Ünlü , Fatih Sultan Mehmet Waqf University, Faculty of Engineering, Department of Electrical and Electronics Engineering, Topkapı, İstanbul, Turkey.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We propose a new way of using law of energy conservation and Faraday tensor for transformation of electromagnetic fields between inertial frames in a four-dimensional Minkowski spacetime wherein space and time are linearly inter-related. We prove that the electromagnetic fields are Lorentz invariant for circular boost along the direction of boost and in perpendicular directions and for a spatial rotation of planes relative to a fixed coordinate axis between two inertial frames. We further demonstrate that the product of covariant and contravariant Faraday tensors and of their duals lead to non-zero electromagnetic field Lagrange density in free space. We also derived Lorentz invariant analytical expressions for Maxwell’s equations, current continuity equation and symmetric electromagnetic field energy-momentum tensor with and without charge and current source. We further demonstrate that using symmetric electromagnetic field energy-momentum tensor one can reliably derive expressions for Lorentz invariant of electromagnetic fields between two inertial frames in case of circular Lorentz boost and spatial (planar) rotation about a fixed coordinate axis. We believe that the proposed theory may have profound effect on the study of contemporary issues in theory of the relativistic electrodynamics and general relativity.
Keywords: Faraday tensor, Conservation of energy, Lorentz invariance, Electromagnetic fields, Maxwell equations, Electromagnetic field energy-momentum tensor, Gravitational field equation
Cite this paper: Hilmi Ünlü , Conservation of Energy and Faraday Tensor in Transformation of Electromagnetic Fields, Maxwell’s Equations, and Symmetric Electromagnetic Field Energy-Momentum Tensor in Theory of Lorentz Invariant Relativistic Electrodynamics, International Journal of Theoretical and Mathematical Physics, Vol. 14 No. 3, 2024, pp. 70-101. doi: 10.5923/j.ijtmp.20241403.02.
Article Outline
1. Introduction
- Maxwell’s equations are the foundation of electrodynamics, and they relate electric and magnetic fields to each other [1]. Historically, Lorentz used Maxwell’s equations to derive his space-time coordinate transformation rule [2]. Einstein in 1905 used Lorentz coordinate transformation rule to prove the validity of Maxwell’s equations in all inertial frames by using two postulates [3]; (i) The physics laws are invariant between two inertial frames. (ii) The speed of light is constant and independent of the direction of the motion of the emitting body in all inertial frames in free space. In electrodynamics, Maxwell’s equations and Lorentz force describe how the charge and current sources with densities
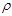 and
and 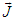 generate electric and magnetic fields (
generate electric and magnetic fields (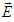 and
and 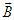 ) [1]:
) [1]: 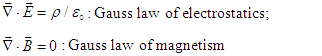 | (1) |
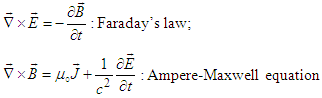 | (2) |
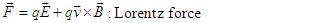 | (3) |
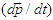 and of energy
and of energy 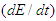 to transform electric and magnetic fields between two inertial frames [4]
to transform electric and magnetic fields between two inertial frames [4]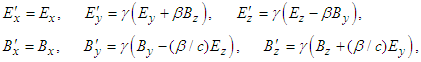 | (4a) |
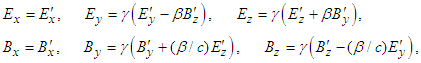 | (4b) |
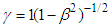 is Lorentz factor with velocity normalized to speed of light
is Lorentz factor with velocity normalized to speed of light 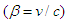 . The electromagnetic field transformation between two inertial frames is also studied by using the electromagnetic field tensor, which is also called Faraday tensor [4]. In this formalism, one uses covariant and contravariant Faraday tensors
. The electromagnetic field transformation between two inertial frames is also studied by using the electromagnetic field tensor, which is also called Faraday tensor [4]. In this formalism, one uses covariant and contravariant Faraday tensors 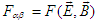 and
and 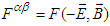 , and their duals
, and their duals 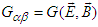 and
and 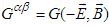 . To obtain the components of
. To obtain the components of  one uses
one uses 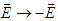 in
in 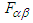 . Likewise, components of dual tensors
. Likewise, components of dual tensors 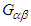 and
and 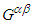 are obtained by using
are obtained by using 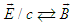 and
and  in
in 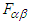 and
and 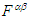 , respectively. For boost along the x-axis, Faraday tensor
, respectively. For boost along the x-axis, Faraday tensor  in frame
in frame 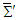 is obtained from the classical transformation
is obtained from the classical transformation 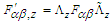 , explicitly written as
, explicitly written as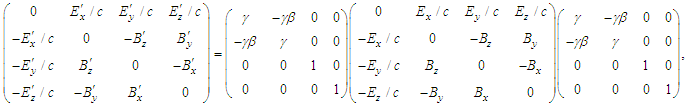 | (5) |
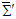 . Likewise, inverse transformation
. Likewise, inverse transformation 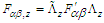 gives the Cartesian components of covariant tensor
gives the Cartesian components of covariant tensor 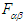 in frame
in frame  , which then yields Eq. (4b).The transformed field equations (4a) and (4b) state that: (i) the electric (magnetic) field are Lorentz invariant along the x-boost direction but not in the y and z directions. (ii) The scalar product of electric and magnetic fields is Lorentz invariant
, which then yields Eq. (4b).The transformed field equations (4a) and (4b) state that: (i) the electric (magnetic) field are Lorentz invariant along the x-boost direction but not in the y and z directions. (ii) The scalar product of electric and magnetic fields is Lorentz invariant 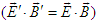 and (iii) the vector product of electric and magnetic fields is not Lorentz invariant
and (iii) the vector product of electric and magnetic fields is not Lorentz invariant 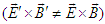 , contradicting Lorentz transformation of vector quantity which must be invariant between two frames
, contradicting Lorentz transformation of vector quantity which must be invariant between two frames 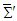 and
and 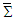 .In the classical Faraday tensor transformation, we observe that (i) Trace of the products of Faraday tensors and their duals is
.In the classical Faraday tensor transformation, we observe that (i) Trace of the products of Faraday tensors and their duals is 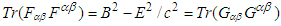 , which has no physical meaning since it yields zero electromagnetic field Lagrange density
, which has no physical meaning since it yields zero electromagnetic field Lagrange density  in free space, which is not realistic because electromagnetic waves transfer energy and momentum [4]. (ii) Furthermore, the trace of covariant and contravariant Faraday tensor and its dual is equal to
in free space, which is not realistic because electromagnetic waves transfer energy and momentum [4]. (ii) Furthermore, the trace of covariant and contravariant Faraday tensor and its dual is equal to 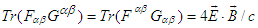 , which suggests that Faraday tensor and its dual are orthogonal when scalar product of electric and magnetic fields is zero. Following the work of Mignani and Recami [9], we recently proposed a 6-dimensional spacetime (3+3) frame [10,11] in which the transformed relativistic velocity is combined with energy conservation to successfully demonstrate the Lorentz invariance of electric and magnetic fields and Maxwell’s equations between two frames under rotation. In this work, we extend our recent study [10], [11] to study Lorentz invariance of relativistic quantities (e.g.position, velocity, momentum, force, electromagnetic fields, Poynting vector, Maxwell’s equations, and energy-momentum tensor in a four-dimensional spacetime in which both space and time coordinates are linearly inter-related. The outline of our presentation is as follows: In sections 2 and 3 we derive the metric equation and transform 4-velocity, 4-momentum and 4-force vector components between two frames. In sections 4 and 5 we use 4-vector velocity with the law of conservation of energy to prove the invariance of electric and magnetic fields under spatial rotation. In sections 6, 7, 8, and 9, we then combine the law of conservation of energy with Faraday tensor and its dual to study Lorentz invariance of electromagnetic fields, Maxwell equations, current continuity equation, and electromagnetic field energy-momentum tensor between two reference frames under a boost and spatial rotation. In section 10, we discuss the details and applications of the proposed theory in invariant relativistic electrodynamics and gravitational field theory.
, which suggests that Faraday tensor and its dual are orthogonal when scalar product of electric and magnetic fields is zero. Following the work of Mignani and Recami [9], we recently proposed a 6-dimensional spacetime (3+3) frame [10,11] in which the transformed relativistic velocity is combined with energy conservation to successfully demonstrate the Lorentz invariance of electric and magnetic fields and Maxwell’s equations between two frames under rotation. In this work, we extend our recent study [10], [11] to study Lorentz invariance of relativistic quantities (e.g.position, velocity, momentum, force, electromagnetic fields, Poynting vector, Maxwell’s equations, and energy-momentum tensor in a four-dimensional spacetime in which both space and time coordinates are linearly inter-related. The outline of our presentation is as follows: In sections 2 and 3 we derive the metric equation and transform 4-velocity, 4-momentum and 4-force vector components between two frames. In sections 4 and 5 we use 4-vector velocity with the law of conservation of energy to prove the invariance of electric and magnetic fields under spatial rotation. In sections 6, 7, 8, and 9, we then combine the law of conservation of energy with Faraday tensor and its dual to study Lorentz invariance of electromagnetic fields, Maxwell equations, current continuity equation, and electromagnetic field energy-momentum tensor between two reference frames under a boost and spatial rotation. In section 10, we discuss the details and applications of the proposed theory in invariant relativistic electrodynamics and gravitational field theory.2. Generalized Four-Dimensional Spacetime
- We introduce a generalized four-dimensional spacetime wherein two “massive inertial frames”
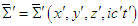 and
and 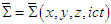 , which coincide with a stationary inertial frame
, which coincide with a stationary inertial frame  at time
at time 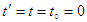 , and move relative to each other with an arbitrary velocity
, and move relative to each other with an arbitrary velocity  . The space and time coordinates are inter-related:
. The space and time coordinates are inter-related:
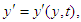
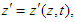
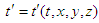 in frame
in frame 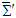 and
and 
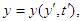
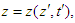 and
and 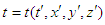 in frame
in frame 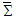 . We require that Einstein’s two postulates are also valid in generalized 4-dimensional spacetime. We consider an event sending a light signal from the origin and second event of arrival at some points
. We require that Einstein’s two postulates are also valid in generalized 4-dimensional spacetime. We consider an event sending a light signal from the origin and second event of arrival at some points 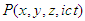 and
and 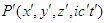 in frames
in frames 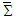 and
and 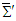 . The square of the displacements are described by
. The square of the displacements are described by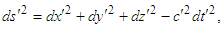 | (6a) |
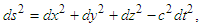 | (6b) |
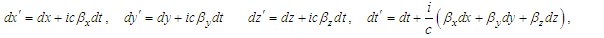 | (7a) |
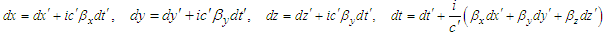 | (7b) |
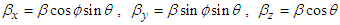 in spherical coordinates with
in spherical coordinates with 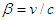 .A pair of events with zero (null) separation connected by a signal at constant speed is described by
.A pair of events with zero (null) separation connected by a signal at constant speed is described by 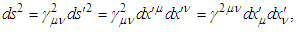 | (8) |
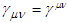 is generalized Minkowski metric tensor. Equation (8) can be written as
is generalized Minkowski metric tensor. Equation (8) can be written as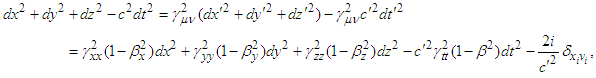 | (9) |
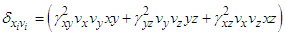 and
and 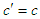 . Matching both sides of Eq. (9) gives
. Matching both sides of Eq. (9) gives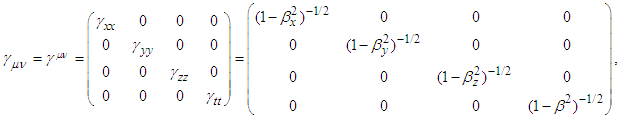 | (10) |
 and.
and. 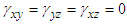 Figure 1 shows that
Figure 1 shows that 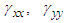 are anisotropic and
are anisotropic and 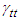 is uniform at any azimuthal angle
is uniform at any azimuthal angle 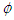 .
.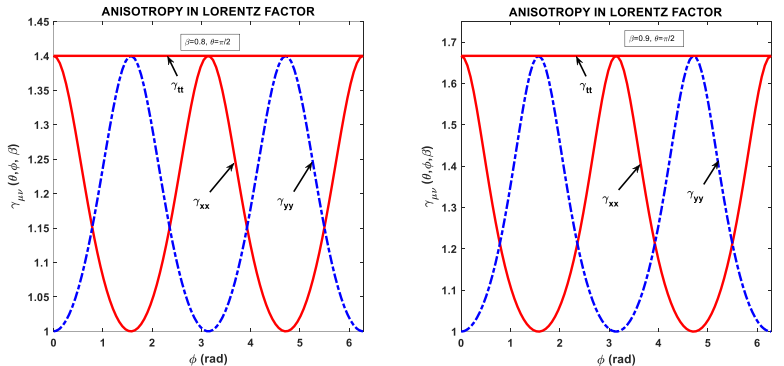 | Figure 1. Cartesian components of Lorentz factor as a function of azimuthal angle  in spherical coordinates for polar angle in spherical coordinates for polar angle  and normalized speed and normalized speed  (left) and (left) and 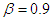 (right) (right) |
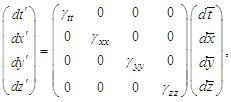 | (11a) |
 | (11b) |
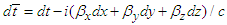 ,
,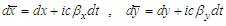 ,
, 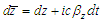 , in frame
, in frame  and
and  ,
, 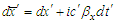 ,
, 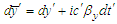 , and
, and 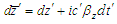 in frame
in frame 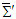 . Equations (11a) and (11b) is rewritten in a familiar matrix form as
. Equations (11a) and (11b) is rewritten in a familiar matrix form as 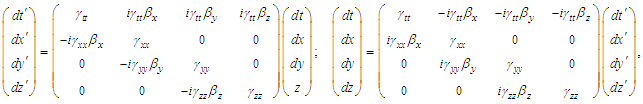 | (12) |
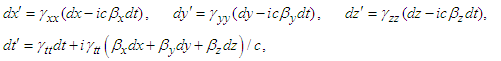 | (13a) |
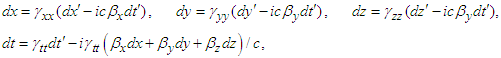 | (13b) |
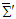 and
and 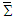
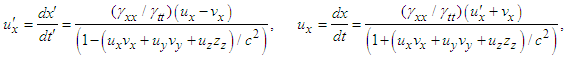 | (14a) |
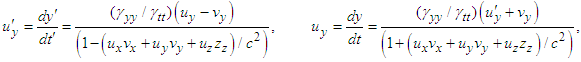 | (14b) |
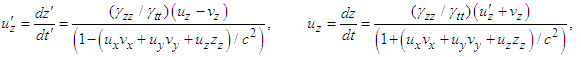 | (14c) |
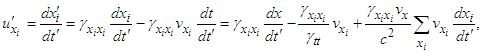 | (15a) |
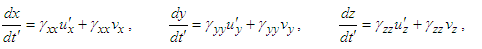 | (15b) |
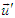 in frame
in frame 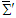 are then written as
are then written as 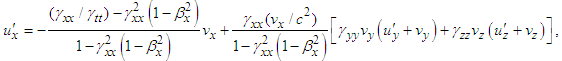 | (16a) |
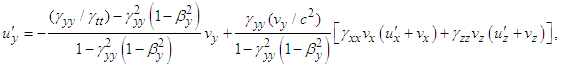 | (16b) |
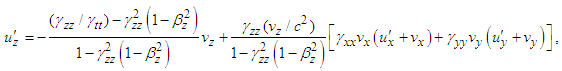 | (16c) |
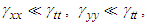 and
and  in Fig. 1, Eqs. (16a), (16b), and 16c) reduce to
in Fig. 1, Eqs. (16a), (16b), and 16c) reduce to 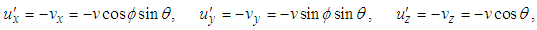 | (17a) |
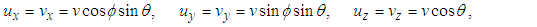 | (17b) |
3. Vector transformation and Four Vectors
- In this section we lay down the groundwork to study the invariance of relativistic vector quantities between two inertial frames. We momentarily set aside the relativity and focus on the three-dimensional vector transformation [12]. Since coordinate systems are used for convenience; we are free to use the following Figure 2 to define stationary 3-dimensional vectors
 and
and 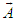 in frames
in frames 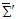 and
and 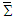 , both of which are initially coincide with a stationary universal inertial frame
, both of which are initially coincide with a stationary universal inertial frame 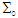 at
at 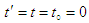 .
. 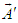 and
and 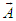 have same length from origin of two frames
have same length from origin of two frames 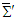 and
and 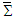 , written as
, written as 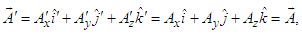 | (18) |
 and
and 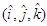 in the massive inertial frames
in the massive inertial frames  and
and  are defined by using the classical vector transformation [12] and are related to each other according to following equations
are defined by using the classical vector transformation [12] and are related to each other according to following equations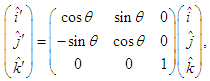 | (19a) |
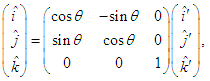 | (19b) |
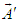 and
and 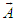 are then written in linear matrix form as [11]
are then written in linear matrix form as [11]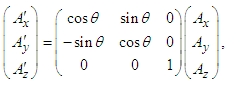 | (20a) |
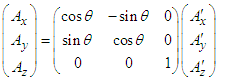 | (20b) |
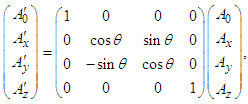 | (21a) |
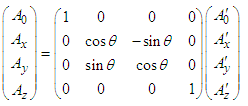 | (21b) |
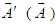 with itself leads to
with itself leads to 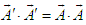 , or
, or 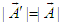 , which states that the magnitude of a vector is Lorentz scalar between frames
, which states that the magnitude of a vector is Lorentz scalar between frames 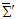 and
and 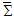 .The 4-vector velocities
.The 4-vector velocities  and
and  are then defined as
are then defined as 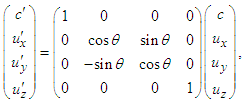 | (22a) |
 | (22b) |
 and
and 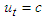 , The scalar product of the 4-velocity vector
, The scalar product of the 4-velocity vector 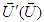 with itself in frame
with itself in frame  is equal to the scalar product of
is equal to the scalar product of  in frame
in frame 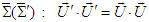 , which allows us to write
, which allows us to write 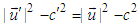 . Since
. Since 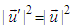 , the speed of light is Lorentz invariant
, the speed of light is Lorentz invariant 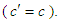 The scalar product of momentum 4-vectors
The scalar product of momentum 4-vectors 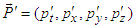 and
and 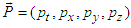 with themselves give the same length
with themselves give the same length 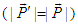 from the origins of two frames. The momentum 4-vector transformation is then identified as a rotation if it causes no change in their magnitudes.
from the origins of two frames. The momentum 4-vector transformation is then identified as a rotation if it causes no change in their magnitudes.4. Conservation of Energy Law and Invariance of Electromagnetic Fields
- We will extend our recently proposed 6-dimensional space-time theory [10,11] to write the following linear matrix equations to describe the 4-force vectors
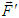 and
and 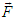 in terms of each other in frames
in terms of each other in frames 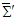 and
and 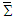
 | (23a) |
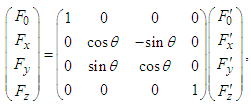 | (23b) |
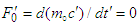 and
and 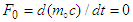 .
. 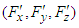 and
and 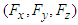 are the Cartesian components of the 3-electromagnetic force vectors (Lorentz force) in the massive inertial frames
are the Cartesian components of the 3-electromagnetic force vectors (Lorentz force) in the massive inertial frames 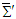 and
and 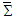 which, according to 3-dimensional vector transformation equations (21a) and (21b), are
which, according to 3-dimensional vector transformation equations (21a) and (21b), are 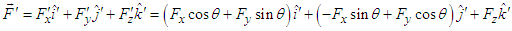 | (24a) |
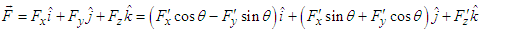 | (24b) |
 in Eqs. (23a) and (23b), unlike the 4-velocity and 4-momentums, force vector is 3-dimensional as defined by Eqs. (24a) and (24b) in terms of unit vectors
in Eqs. (23a) and (23b), unlike the 4-velocity and 4-momentums, force vector is 3-dimensional as defined by Eqs. (24a) and (24b) in terms of unit vectors  and
and  in frames
in frames 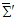 and
and  . The scalar product of
. The scalar product of 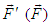 with itself leads to
with itself leads to 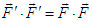 , or
, or 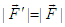 . The rates at which work is done on a particle by Lorentz force in frames
. The rates at which work is done on a particle by Lorentz force in frames 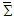 and
and 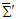 are
are 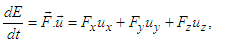 | (25a) |
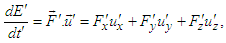 | (25b) |
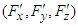 and
and 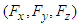 are Cartesian components of Lorentz force in frames
are Cartesian components of Lorentz force in frames 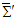 and
and  .
.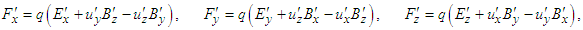 | (26a) |
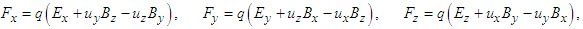 | (26b) |
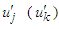 and
and 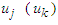 and are Cartesian components of
and are Cartesian components of  and
and 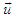 in Eqs. (22a) and (22b).Considering the massive inertial frames
in Eqs. (22a) and (22b).Considering the massive inertial frames  and
and 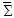 form a closed system in the stationary spacetime frame
form a closed system in the stationary spacetime frame 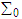 , the law of conservation of power (or energy) between them is written as
, the law of conservation of power (or energy) between them is written as 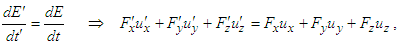 | (27) |
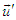 and
and 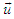 , Eq. (27) is written as
, Eq. (27) is written as 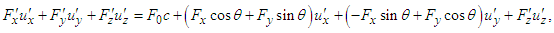 | (28a) |
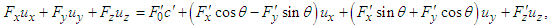 | (28b) |
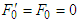 . Using Eqs. (26a) and (26b) in Eq. (28a), we can write following equations
. Using Eqs. (26a) and (26b) in Eq. (28a), we can write following equations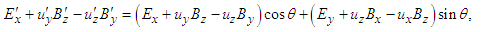 | (29a) |
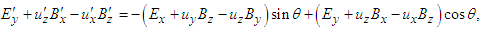 | (29b) |
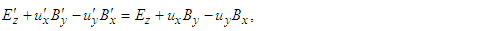 | (29c) |
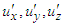 in Eqs. (29a), (29b), and (29c), we write following matrix equations
in Eqs. (29a), (29b), and (29c), we write following matrix equations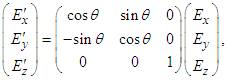 | (30a) |
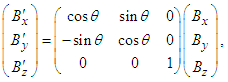 | (30b) |
 in Eqs. (29a), (29b), and (29c) for inverse transformation, we write
in Eqs. (29a), (29b), and (29c) for inverse transformation, we write 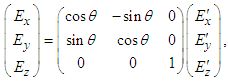 | (30c) |
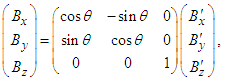 | (30d) |
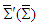 is composed of electric (or magnetic) field in frame
is composed of electric (or magnetic) field in frame 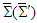 for spatial rotation of (x, y) plane about z-axis. The scalar and vector products of electric and magnetic fields is essential in proving Lorentz invariance of electromagnetic energy, Poynting vector, current continuity equation, and densities of electromagnetic field energy and momentum. Using Eqs. (30a) -(30d) one writes
for spatial rotation of (x, y) plane about z-axis. The scalar and vector products of electric and magnetic fields is essential in proving Lorentz invariance of electromagnetic energy, Poynting vector, current continuity equation, and densities of electromagnetic field energy and momentum. Using Eqs. (30a) -(30d) one writes 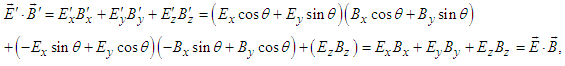 | (31a) |
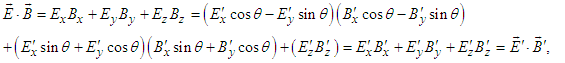 | (31b) |
 and
and 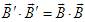 , so that
, so that 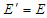 and
and 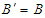 (Lorentz scalar invariants). The vector products of
(Lorentz scalar invariants). The vector products of  and
and 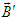 in frame
in frame 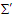 and of
and of 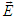 and
and 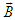 frames
frames 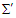 and
and 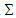 are
are 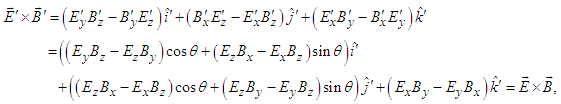 | (32a) |
 | (32b) |
 is Lorentz invariant vector between the frames
is Lorentz invariant vector between the frames 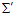 and
and  .
.5. Conservation of Energy and Faraday Tensor in Field Transformation
- We will extend 3-dimensional Lorentz force
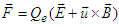 to 4-dimensions as covariant and contravariant Lorentz tensors
to 4-dimensions as covariant and contravariant Lorentz tensors 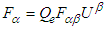 and
and 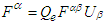 , respectively. Here
, respectively. Here  is the static electric charge,
is the static electric charge, 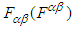 is the covariant contravariant antisymmetric second rank tensor, also known as Faraday tensor.
is the covariant contravariant antisymmetric second rank tensor, also known as Faraday tensor. 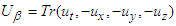 and
and 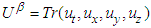 are covariant and contravariant 4-vector velocities. Considering the frames
are covariant and contravariant 4-vector velocities. Considering the frames 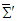 and
and  form a closed system in the stationary frame
form a closed system in the stationary frame 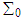 , the law of conservation of power (energy) equation (27) can be written as
, the law of conservation of power (energy) equation (27) can be written as 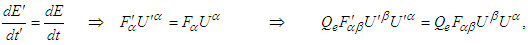 | (33) |
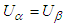 and
and  . Using
. Using 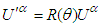 and
and 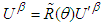 in Eq. (33) we write the following rule to transform
in Eq. (33) we write the following rule to transform 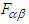 in
in  into
into 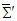 for a counter-clockwise rotation about z-axis.
for a counter-clockwise rotation about z-axis.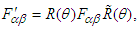 | (34) |
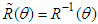 is the transpose (inverse) of rotation matrix
is the transpose (inverse) of rotation matrix 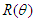 . In tensor analysis, the covariant (contravariant) tensor
. In tensor analysis, the covariant (contravariant) tensor 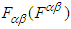 is defined as vector product of any two vectors
is defined as vector product of any two vectors 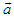 and
and 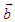 is another vector
is another vector 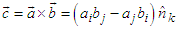 and considered as second rank antisymmetric tensor [4], with
and considered as second rank antisymmetric tensor [4], with  . Covariant and contravariant 4-Lorentz forces as 4-tensors are defined as
. Covariant and contravariant 4-Lorentz forces as 4-tensors are defined as 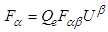 and
and 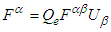 in frame
in frame  , written as
, written as | (35a) |
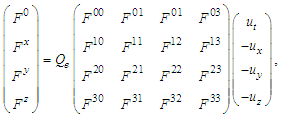 | (35b) |
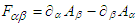 is second rank antisymmetric covariant field tensor, also called Faraday tensors, with
is second rank antisymmetric covariant field tensor, also called Faraday tensors, with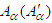 being any arbitrary 4-vector in frames
being any arbitrary 4-vector in frames 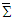 and
and 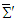 .
. 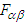 are defined as
are defined as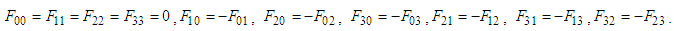 Similarly, one can define the contravariant Faraday tensor
Similarly, one can define the contravariant Faraday tensor 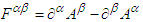 . Dual Faraday tensor transformation between frames
. Dual Faraday tensor transformation between frames  and
and  is defined like Faraday tensor transformation equation (33). To do that we first introduce a “fictitious” magnetic charge
is defined like Faraday tensor transformation equation (33). To do that we first introduce a “fictitious” magnetic charge 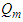 [13] and define “fictitious” dual Lorentz force
[13] and define “fictitious” dual Lorentz force 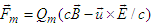 by using electromagnetic duality
by using electromagnetic duality 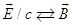 and
and  in conventional Lorentz force
in conventional Lorentz force 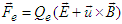 . Here
. Here 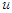 is the velocity of moving electrical charge. We then define 4- dual covariant and contravariant Lorentz tensors in frame
is the velocity of moving electrical charge. We then define 4- dual covariant and contravariant Lorentz tensors in frame  as
as 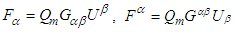 . Using
. Using 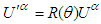 and
and 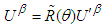 we can write the following rule to transform
we can write the following rule to transform 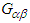 in
in 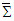 into
into  for a counter-clockwise rotation about z-axis.
for a counter-clockwise rotation about z-axis. | (36) |
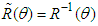 is the transpose (inverse) of rotation matrix
is the transpose (inverse) of rotation matrix 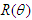 . Covariant and contravariant fictitious 4-vector dual Lorentz forces
. Covariant and contravariant fictitious 4-vector dual Lorentz forces  and
and 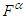 in frame
in frame  are then written as
are then written as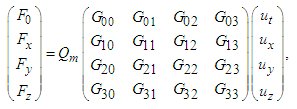 | (37a) |
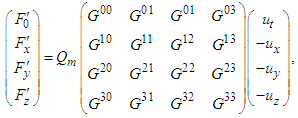 | (37b) |
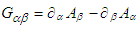 is antisymmetric second rank covariant field tensor. Similarly, one can define contravariant dual tensor
is antisymmetric second rank covariant field tensor. Similarly, one can define contravariant dual tensor 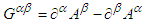 . Components of the covariant (contravariant) dual tensors
. Components of the covariant (contravariant) dual tensors 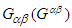 are then obtained by using
are then obtained by using 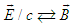 and
and 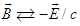 in
in 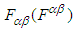 . To eliminate the unnoticed error made in the classical use of Faraday tensor in field transformation [4] we use the generalized 4-dimensional Minkowski spacetime wherein 4-vector space coordinates are
. To eliminate the unnoticed error made in the classical use of Faraday tensor in field transformation [4] we use the generalized 4-dimensional Minkowski spacetime wherein 4-vector space coordinates are 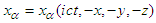 and
and 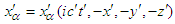 in frames
in frames 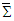 and
and 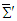 . Using the covariant 4-vector potentials
. Using the covariant 4-vector potentials 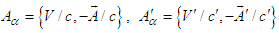 and multiplying
and multiplying 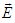 and
and 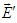 with
with 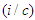 and
and 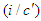 the electric and magnetic fields in frames
the electric and magnetic fields in frames 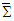 and
and 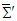 are written as
are written as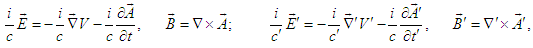 | (38) |
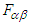 with the following Cartesian components in frame
with the following Cartesian components in frame 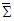
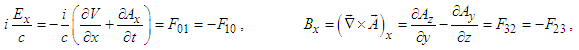 | (39a) |
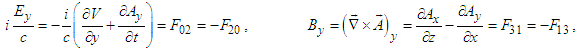 | (39b) |
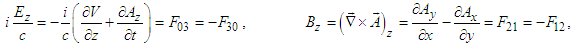 | (39c) |
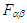 and
and  , and their duals
, and their duals 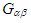 and
and 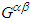 in frame
in frame 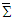 are
are  | (40a) |
 | (40b) |
 | (40c) |
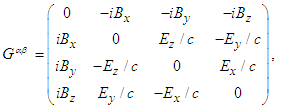 | (40d) |
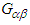 and
and 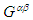 are constructed by using the so called the electromagnetic duality
are constructed by using the so called the electromagnetic duality 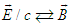 and
and 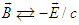 in Faraday tensors
in Faraday tensors 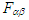 and
and 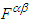 . Using equations (40a), (40b), (40c), and (40d) for the covariant and contravariant Faraday tensors (
. Using equations (40a), (40b), (40c), and (40d) for the covariant and contravariant Faraday tensors (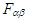 and
and 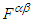 ) and their duals (
) and their duals (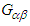 and
and 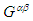 ), one can write the following matrix expressions for the products
), one can write the following matrix expressions for the products 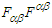 and of their duals
and of their duals 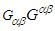 in frame
in frame 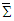
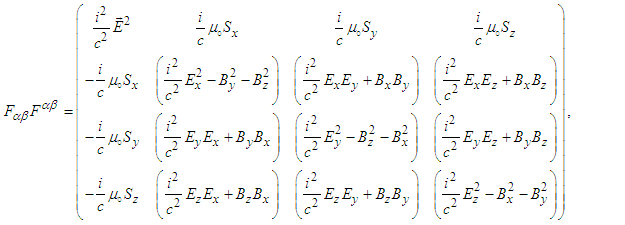 | (41) |
 | (42) |
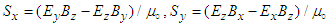 , and
, and 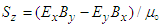 are the x, y, and z components of the Poynting vector. Traces of
are the x, y, and z components of the Poynting vector. Traces of 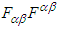 and of
and of 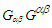 are nonzero:
are nonzero: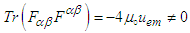 | (43a) |
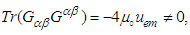 | (43b) |
 | (44a) |
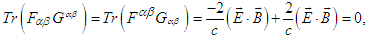 | (44b) |
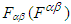 and
and 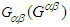 are orthogonal only when
are orthogonal only when 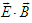 is zero. Equation. (44b) suggests that
is zero. Equation. (44b) suggests that 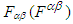 and
and 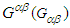 are always orthogonal in frames
are always orthogonal in frames 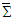 and
and 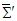 .
.6. Faraday Tensor in Electromagnetic Field Transformation
- The incremental displacement of a coordinate system relative to its initial position is known to be composed of a translation as well as a rotation. While the components of 4-vector quantities transform according to Eq. (21a) and (21b), the spatial translation has no effect on them. One can use Faraday tensors and their duals determine the components of electric and magnetic fields in frames
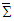 and
and 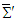 by using: (i) Lorentz boost along the direction of motion, which is appropriate transformation for relative motion of two observers, and(ii) Spatial rotation, which relates spacetime coordinates of two observers in two frames which are subject to planar rotation with respect to each other about a fixed axis.
by using: (i) Lorentz boost along the direction of motion, which is appropriate transformation for relative motion of two observers, and(ii) Spatial rotation, which relates spacetime coordinates of two observers in two frames which are subject to planar rotation with respect to each other about a fixed axis. 6.1. Faraday Tensor and Field Transformation with Lorentz Boost
- We use
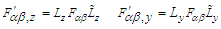 , and
, and 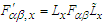 transformation rules to transform electromagnetic fields between frames
transformation rules to transform electromagnetic fields between frames 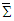 and
and 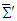 for Lorentz boost along x, y, and z-axes, which are written as
for Lorentz boost along x, y, and z-axes, which are written as | (45) |
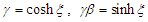 with
with 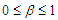 and
and 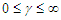 . Here
. Here  is called the boost parameter [4]. For a Lorentz boost along x-axis, the transformation
is called the boost parameter [4]. For a Lorentz boost along x-axis, the transformation 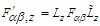 allows us to obtain the Cartesian components of Faraday tensor in frame
allows us to obtain the Cartesian components of Faraday tensor in frame 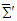 in terms of those in frame
in terms of those in frame 
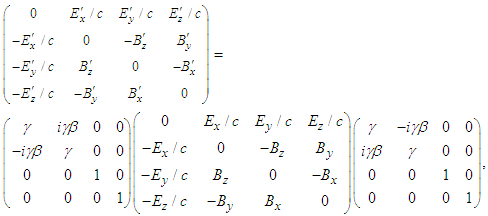 | (46) |
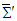 in terms of those in frame
in terms of those in frame 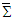 . Transformation
. Transformation 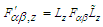 and
and 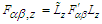 yield electric and magnetic field components in frames
yield electric and magnetic field components in frames 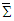 and
and 
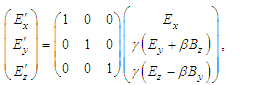 | (47a) |
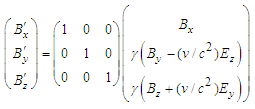 | (47b) |
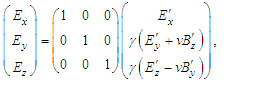 | (47c) |
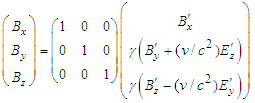 | (47d) |
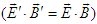 and non-invariant vector product
and non-invariant vector product 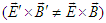 between two frames under Lorentz transformation. In the next step, we introduce a circular boost, rather than hyperbolic one defined in Eq. (45), for motion along x, y, and z- axes in frame
between two frames under Lorentz transformation. In the next step, we introduce a circular boost, rather than hyperbolic one defined in Eq. (45), for motion along x, y, and z- axes in frame 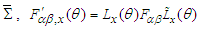 to find
to find 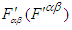 , which are
, which are 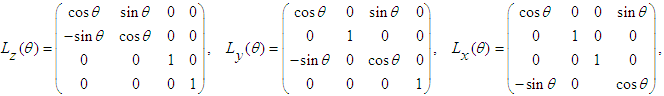 | (48) |
 in frame
in frame  are obtained by using the transformation rule
are obtained by using the transformation rule 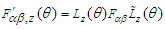 , which is explicitly written as
, which is explicitly written as 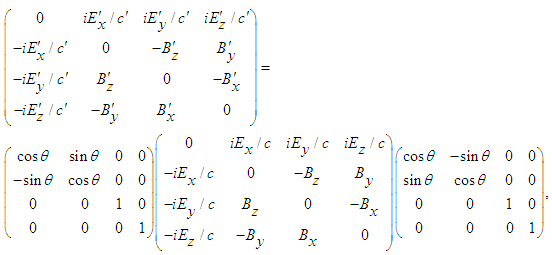 | (49) |
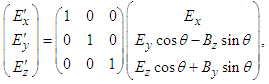 | (50a) |
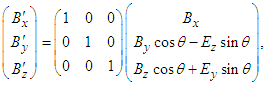 | (50b) |
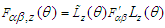 one writes
one writes 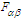 in frame
in frame  and obtain
and obtain 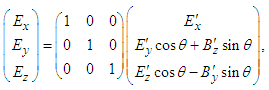 | (50c) |
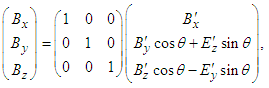 | (50d) |
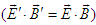 between frames
between frames 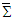 and
and  . The vector products of electric and magnetic in frames
. The vector products of electric and magnetic in frames 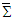 and
and 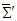 fields are
fields are 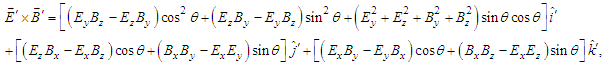 | (51a) |
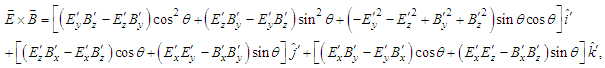 | (51b) |
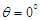 unit vectors are equivalent in both frames
unit vectors are equivalent in both frames 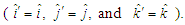 Eqs. (51a) and (51b) yield
Eqs. (51a) and (51b) yield  and
and  , contrary to the hyperbolic boosts in Eq. (45).
, contrary to the hyperbolic boosts in Eq. (45). 6.2. Faraday Tensor and Field Transformation with Spatial Rotations
- It is possible to combine boosts with rotations to relate the electromagnetic fields to each other between the frames
 and
and  , by using counterclockwise rotations of (x, y), (z, x), and (y, z) planes about z, y and x-axes, which are given by the following expressions
, by using counterclockwise rotations of (x, y), (z, x), and (y, z) planes about z, y and x-axes, which are given by the following expressions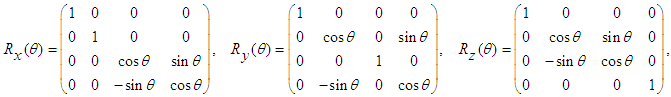 | (52) |
 with
with  one writes expressions for the clockwise rotation about x, y, and z-axes. As an example, the transformation
one writes expressions for the clockwise rotation about x, y, and z-axes. As an example, the transformation 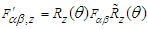 allows us to determine the components of covariant Faraday tensor
allows us to determine the components of covariant Faraday tensor 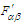 in frame
in frame 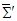 in terms of the components of covariant
in terms of the components of covariant 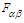 in frame
in frame 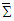
 | (53) |
 one writes similar equation for
one writes similar equation for  in frame
in frame 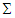 . Matching both sides of Eq. (53) and of its inverse, one writes following matrix equations
. Matching both sides of Eq. (53) and of its inverse, one writes following matrix equations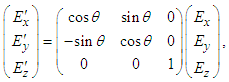 | (54a) |
 | (54b) |
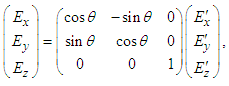 | (54c) |
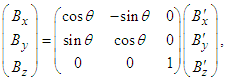 | (54d) |
 and
and 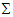 ,
, 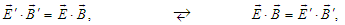 | (55a) |
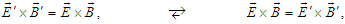 | (55b) |
 and
and  .
.7. Faraday Tensor and Invariance of Maxwell’s Equations
- Using
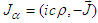 in
in  and
and 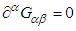 with
with 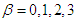 for
for 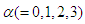 we write
we write 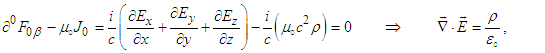 | (56a) |
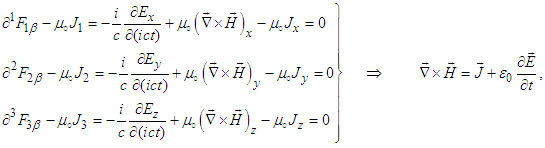 | (56b) |
 | (57a) |
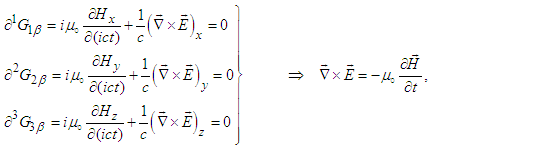 | (57b) |
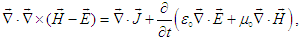 | (58) |
 and
and 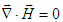 , equation (58) results in the conventional current continuity equation written as
, equation (58) results in the conventional current continuity equation written as | (59) |
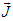 and
and 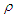 are the total current and charge densities, respectively. In the following subsections we will prove that inhomogeneous and homogeneous Maxwell equations (56) and (57) are Lorentz invariant between two massive inertial frames. Recall the following expressions for the flux of a vector field through a spherical closed surface in frames
are the total current and charge densities, respectively. In the following subsections we will prove that inhomogeneous and homogeneous Maxwell equations (56) and (57) are Lorentz invariant between two massive inertial frames. Recall the following expressions for the flux of a vector field through a spherical closed surface in frames  and
and 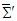
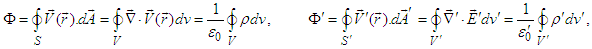 | (60) |
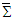 and
and 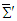
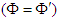 , we write the following chain rules of differentiation
, we write the following chain rules of differentiation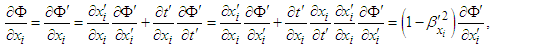 | (61) |
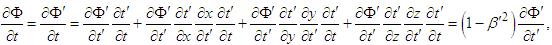 | (62) |
7.1. Gauss Law of Electrostatics
- Since electric field wave function is continuous at any point in space, taking
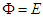 and
and 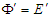 , and applying chain rule in Eq. (61) we write the charge density
, and applying chain rule in Eq. (61) we write the charge density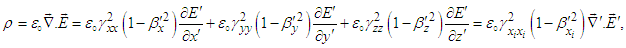 | (63) |
 . Since
. Since  and
and 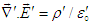 , matching both sides of Eq. (63) yields
, matching both sides of Eq. (63) yields 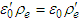 . where
. where 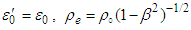 and
and 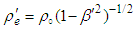 are the charge densities in frames
are the charge densities in frames 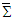 and
and 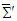 , defined with respect to charge density
, defined with respect to charge density 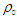 in frame
in frame 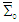 . We can write
. We can write 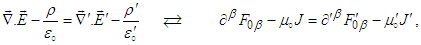 | (64) |
 and
and  .
.7.2. Gauss Law of Magnetostatics
- Since magnetic field wave function is continuous at any point in space, taking
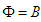 and
and 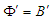 , and using chain rule in Eq. (61), we write
, and using chain rule in Eq. (61), we write 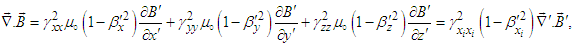 | (65) |
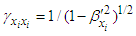 for the space component of Lorentz scaling factor in Eq. (10), and covariant Eq. (65) is transformed into the invariant form
for the space component of Lorentz scaling factor in Eq. (10), and covariant Eq. (65) is transformed into the invariant form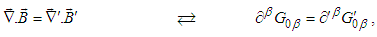 | (66) |
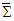 and
and  .
.7.3. Faraday’s Law of Induction
- Let us re-write the differential form of Faraday’s law of induction in Eq. (57b) in x, y, and z-directions of the Cartesian coordinates in frame

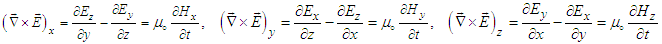 | (67) |
 | (68a) |
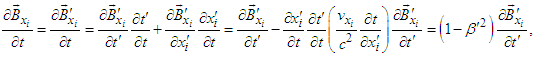 | (68b) |
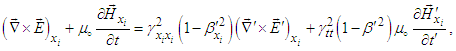 | (69) |
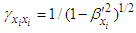 and
and 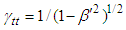 for components of Lorentz scaling factor in Eq. (10). Covariant Eq. (69) is then transformed into invariant form
for components of Lorentz scaling factor in Eq. (10). Covariant Eq. (69) is then transformed into invariant form | (70) |
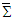 and
and  .
.7.4. Ampere-Maxwell Equation
- Ampere-Maxwell’s equation (57b) are written as
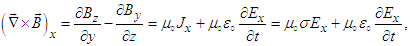 | (71a) |
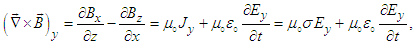 | (71b) |
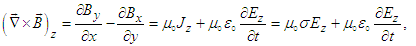 | (71c) |
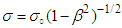 and
and 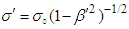 are the conductivities in frames
are the conductivities in frames  and
and  , defined relative to
, defined relative to  in the steady inertial frame
in the steady inertial frame 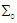 . Applying the chain rule in Eq. (61) and (62) to differential form of Ampere-Faraday’s law in x, y, and z-directions and write
. Applying the chain rule in Eq. (61) and (62) to differential form of Ampere-Faraday’s law in x, y, and z-directions and write 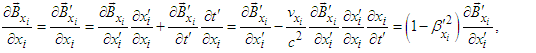 | (72a) |
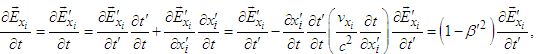 | (72b) |
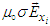 and
and 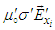 , we write
, we write 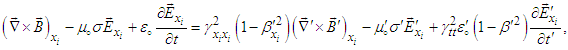 | (73) |
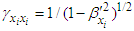 and
and  for space-time components of Lorentz scaling factor in Eq. (10). Then covariant Eq. (73) becomes invariant
for space-time components of Lorentz scaling factor in Eq. (10). Then covariant Eq. (73) becomes invariant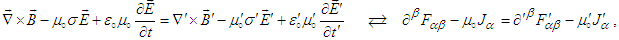 | (74) |
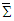 and
and 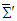 .
.7.5. Current Continuity Equation
- Since Maxwell’s equations must satisfy the charge (current) continuity equation, using chain rules in Eqs. (61) and (62) we can write
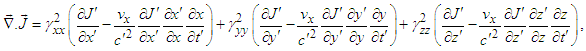 | (75a) |
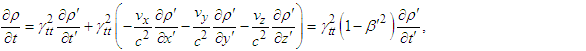 | (75b) |
 and
and 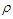 are the total current and charge densities, respectively. Side by side additions of Eqs. (75a) and (75b) allows us to write the following covariant equation
are the total current and charge densities, respectively. Side by side additions of Eqs. (75a) and (75b) allows us to write the following covariant equation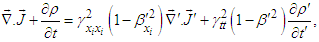 | (76) |
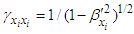 and
and 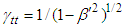 in Eq. (10), and
in Eq. (10), and  | (77) |
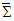 and
and 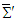 .
.8. Symmetric Electromagnetic Energy-Momentum Tensor and Conservation Laws
- The classical symmetric energy-momentum tensor is described by a second rank tensor [4]
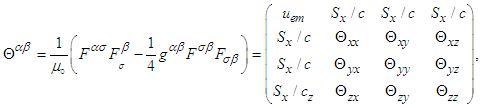 | (78) |
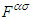 is the contravariant field tensor and
is the contravariant field tensor and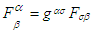
 is mixed tensor, with
is mixed tensor, with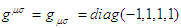 .
. 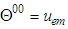 is energy density,
is energy density, 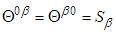 is Cartesian components of Poynting vector, and
is Cartesian components of Poynting vector, and 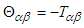 , with Maxwell’s stress tensor
, with Maxwell’s stress tensor 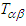 defined as [4]
defined as [4]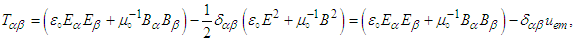 | (79) |
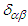 is the Kronecker delta which is unity if
is the Kronecker delta which is unity if 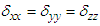 and zero otherwise [4]. Mixed tensor
and zero otherwise [4]. Mixed tensor 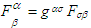
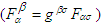 in Eq. (78) has no explicit symmetry characteristics [4]. Consequently, we pursued a search for an alternative way to derive Lorentz invariant expression for a symmetric electromagnetic energy-momentum tensor. We discovered that the average sum of the product of covariant-contravariant Faraday tensor and transpose of the contravariant covariant dual Faraday tensors
in Eq. (78) has no explicit symmetry characteristics [4]. Consequently, we pursued a search for an alternative way to derive Lorentz invariant expression for a symmetric electromagnetic energy-momentum tensor. We discovered that the average sum of the product of covariant-contravariant Faraday tensor and transpose of the contravariant covariant dual Faraday tensors  fits our requirement of the electromagnetic energy-momentum tensor. In the massive inertial frame
fits our requirement of the electromagnetic energy-momentum tensor. In the massive inertial frame 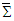 they are written as
they are written as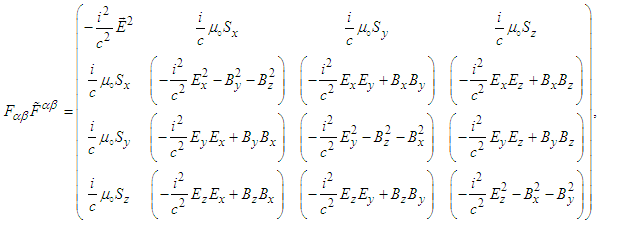 | (80) |
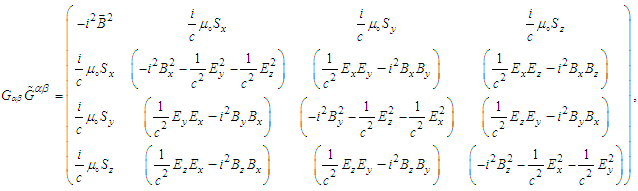 | (81) |
 | (82) |
 in frame
in frame  is then written as
is then written as | (83) |
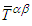 in Eq. (82) are
in Eq. (82) are 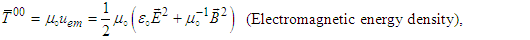 | (84a) |
 | (84b) |
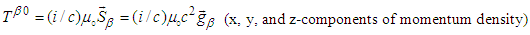 | (84c) |
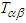 is given by Eq. (79). Since
is given by Eq. (79). Since 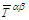 is symmetric
is symmetric 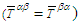 its trace must be zero:
its trace must be zero: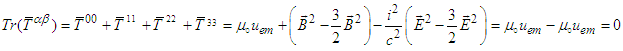 | (85) |
9. Poynting Theorem and Conservation Laws
- Using
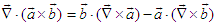 and Maxwell’s equations (56) and (57), divergence of Poynting vector can be written as
and Maxwell’s equations (56) and (57), divergence of Poynting vector can be written as 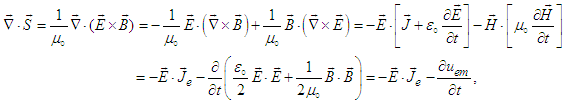 | (86) |
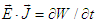 is the rate of work done by Lorentz force on moving charged particles and
is the rate of work done by Lorentz force on moving charged particles and 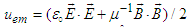 is the electromagnetic energy density. Divergence theorem yields
is the electromagnetic energy density. Divergence theorem yields 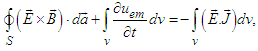 | (87) |
 allows us to derive differential form of Poynting theorem and conservation of linear momentum with charge and current sources. Using the 4-vector current density
allows us to derive differential form of Poynting theorem and conservation of linear momentum with charge and current sources. Using the 4-vector current density 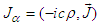 in
in 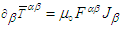 we write
we write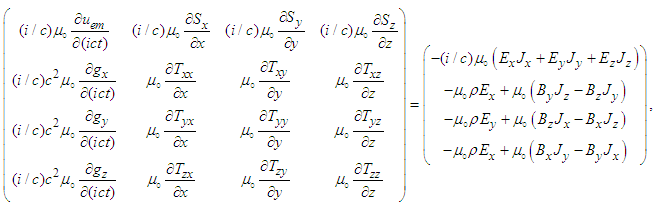 | (88) |
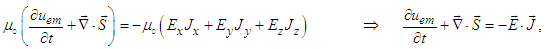 | (89) |
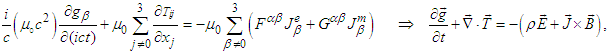 | (90) |
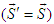 , letting
, letting  (or
(or  ) and
) and  (or
(or 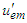 ), Eq. (89) can be decomposed as
), Eq. (89) can be decomposed as  | (91a) |
 | (91b) |
 | (91c) |
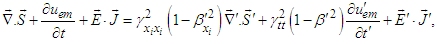 | (92) |
 and
and 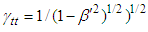 in Eq. (10), which transforms covariant equation Eq. (92) into the following invariant form
in Eq. (10), which transforms covariant equation Eq. (92) into the following invariant form  | (93) |
 | (94a) |
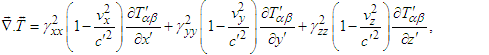 | (94b) |
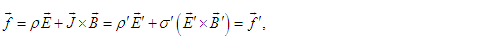 | (94c) |
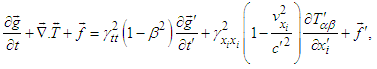 | (95) |
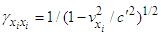 and
and 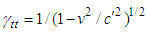 in Eq. (10) for components of Lorentz factor and covariant Eq. (95) is transformed invariant form
in Eq. (10) for components of Lorentz factor and covariant Eq. (95) is transformed invariant form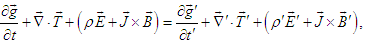 | (96) |
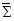 and
and 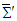 .
. 10. Results and Discussions
- In this work, we introduced so called generalized 4-dimensional massive inertial frames
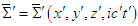 and
and 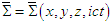 , both coincide with stationary inertial frame
, both coincide with stationary inertial frame 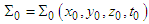 at time
at time 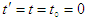 , and move relative to each other with arbitrary velocity
, and move relative to each other with arbitrary velocity 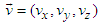 . The space and time coordinates are interrelated:
. The space and time coordinates are interrelated: 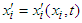 ,
, 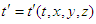 in
in 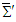 and
and 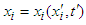 ,
, 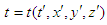 in frame
in frame 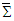 , where
, where 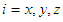 . We derived the generalized 4-dimensional spacetime metric equation (8), with Lorentz scaling factor in Eq. (10), which has anisotropic space and uniform time components. The role of this factor on the invariance of relativistic quantities such as energy, momentum, mass, time dilation and Doppler shift is discussed in appendix. In the following, we discuss Lorentz invariance of electromagnetic fields, Maxwell’s equations, and symmetric electromagnetic field energy-momentum tensor.
. We derived the generalized 4-dimensional spacetime metric equation (8), with Lorentz scaling factor in Eq. (10), which has anisotropic space and uniform time components. The role of this factor on the invariance of relativistic quantities such as energy, momentum, mass, time dilation and Doppler shift is discussed in appendix. In the following, we discuss Lorentz invariance of electromagnetic fields, Maxwell’s equations, and symmetric electromagnetic field energy-momentum tensor.10.1. Comparison of Classical and New Way of Using Faraday Tensor in Field Transformation
- By using the 4- velocity and 4-force vectors in the energy conservation law we demonstrated the Lorentz invariance of the scalar and vector products of electric and magnetic fields between two so called massive inertial frames for a spatial rotation about a fixed axis. As an example, consider point charge Q in frame
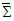 . The produced electric and magnetic fields in frames
. The produced electric and magnetic fields in frames 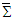 and
and 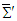 are
are 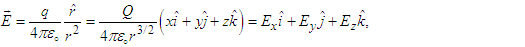 | (97a) |
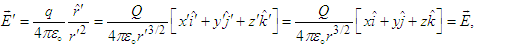 | (97b) |
 | (97c) |
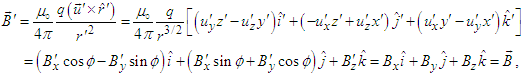 | (97d) |
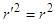 . One can show that the scalar and vector products of electric and magnetic fields are Lorentz invariant
. One can show that the scalar and vector products of electric and magnetic fields are Lorentz invariant 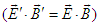 and
and 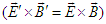 between two massive inertial frames. To confirm the findings in section 4, we focused on the use of electromagnetic field strength tensor, also called Faraday tensor in sections 5 and 6 to derive expressions for the invariant electromagnetic fields. We demonstrated that the hyperbolic boost along x-axis classical use of Faraday tensor in field transformation
between two massive inertial frames. To confirm the findings in section 4, we focused on the use of electromagnetic field strength tensor, also called Faraday tensor in sections 5 and 6 to derive expressions for the invariant electromagnetic fields. We demonstrated that the hyperbolic boost along x-axis classical use of Faraday tensor in field transformation  given Eq. (6) and
given Eq. (6) and 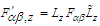 (45) for Lorentz boosts along the x, y and z-axes, lead to a non-invariant vector product of electric and magnetic fields, and in turn non-invariant Poynting vector, between two inertial frames. For a Lorentz boost along x-axis, one can use the transformation
(45) for Lorentz boosts along the x, y and z-axes, lead to a non-invariant vector product of electric and magnetic fields, and in turn non-invariant Poynting vector, between two inertial frames. For a Lorentz boost along x-axis, one can use the transformation  to find components of Faraday tensor in frame
to find components of Faraday tensor in frame 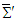 in terms of those in frame
in terms of those in frame 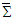 . Transformation
. Transformation  and its inverse
and its inverse 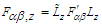 yield Cartesian components of the electric and magnetic fields in frames
yield Cartesian components of the electric and magnetic fields in frames 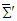 and
and 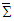 in terms of each other, given by Eqs. (47a), (47b), (47c), and (47d), respectively. They are the same as Eqs. (4a) and (4b), with
in terms of each other, given by Eqs. (47a), (47b), (47c), and (47d), respectively. They are the same as Eqs. (4a) and (4b), with  and
and 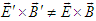 . In zero velocity case, Eqs. (47a), (47b), (47c), and (47d) results in invariant vector product. However, this has no relativistic meaning since zero velocity case means that two frames coincide with each other at rest. In the case of circular Lorentz boosts about the x, y, and z-axes given by Eq. (48), the result of Faraday tensor transformations surprisingly turns out to be quite different. For example, the circular Lorentz boost along x-axis with fixed z-axis, transformation
. In zero velocity case, Eqs. (47a), (47b), (47c), and (47d) results in invariant vector product. However, this has no relativistic meaning since zero velocity case means that two frames coincide with each other at rest. In the case of circular Lorentz boosts about the x, y, and z-axes given by Eq. (48), the result of Faraday tensor transformations surprisingly turns out to be quite different. For example, the circular Lorentz boost along x-axis with fixed z-axis, transformation 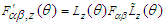 yields components of covariant Faraday tensor
yields components of covariant Faraday tensor  in frame
in frame 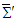 , which leads to Cartesian components of electromagnetic fields in frame
, which leads to Cartesian components of electromagnetic fields in frame 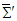 as mixture of those in frame
as mixture of those in frame 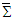 at any angle, according to Eqs. (50). However, as easily seen from Eqs. (51) and (52) for
at any angle, according to Eqs. (50). However, as easily seen from Eqs. (51) and (52) for 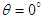 , contrary to the hyperbolic Lorentz boost in Eq. (47), the vector products of electric and magnetic fields is Lorentz invariant
, contrary to the hyperbolic Lorentz boost in Eq. (47), the vector products of electric and magnetic fields is Lorentz invariant 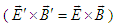 between frames
between frames 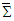 and
and  . This may be due to the difference between hyperbolic boosts in Eq. (45) and circular boost Eq. (48), which are derived from translational and rotational points of views for which
. This may be due to the difference between hyperbolic boosts in Eq. (45) and circular boost Eq. (48), which are derived from translational and rotational points of views for which 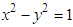 and
and 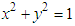 , respectively, in two dimensions.In section 6.2 we demonstrated that if two frames
, respectively, in two dimensions.In section 6.2 we demonstrated that if two frames 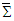 and
and 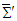 are related by spatial rotation of (x, y) plane with fixed z-axis, of (y, z) plane about x axis, and (z, x) plane about y axis, respectively, Cartesian components of covariant (contravariant) Faraday tensor
are related by spatial rotation of (x, y) plane with fixed z-axis, of (y, z) plane about x axis, and (z, x) plane about y axis, respectively, Cartesian components of covariant (contravariant) Faraday tensor 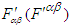 in frame
in frame 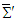 can be found according to the spatial rotation transformations given by Eq. (52). For a spatial rotation of (x,y) plane about the z-axis, covariant Faraday tensor in frame
can be found according to the spatial rotation transformations given by Eq. (52). For a spatial rotation of (x,y) plane about the z-axis, covariant Faraday tensor in frame 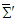 is obtained from
is obtained from 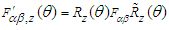 , which yields Lorentz invariant electric and magnetic fields in frame
, which yields Lorentz invariant electric and magnetic fields in frame 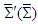 in terms of those in frame
in terms of those in frame 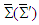 according to Eqs. (54a) - (54d). Similar results are found under the spatial rotation of (y, z) plane about x-axis, and (z, x) plane about the y-axis, respectively.
according to Eqs. (54a) - (54d). Similar results are found under the spatial rotation of (y, z) plane about x-axis, and (z, x) plane about the y-axis, respectively. 10.2. Faraday Tensor and Lagrange Density of Electromagnetic Field
- In section 6 we also proved that the new way of using Faraday transformation under the spatial rotations about fixed coordinate axes lead to Lorentz invariant properties (e.g., Poynting vector, inhomogeneous and homogeneous Maxwell’s equations, and equations of continuity) between two frames
 and
and 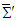 , respectively. Considering a charged particles moving under the influence of an external electromagnetic field we use so called the action principle
, respectively. Considering a charged particles moving under the influence of an external electromagnetic field we use so called the action principle 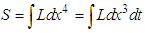 to derive its equation of motion [18]. Here L is the total Lagrange density of the charged particle which is equal to sum of the free space
to derive its equation of motion [18]. Here L is the total Lagrange density of the charged particle which is equal to sum of the free space 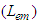 and external source
and external source  contributions and is written as
contributions and is written as 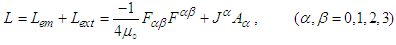 | (98) |
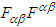 and of their duals
and of their duals 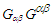 are non-zero and yield a nonzero electromagnetic energy density in free space. Consequently, we write
are non-zero and yield a nonzero electromagnetic energy density in free space. Consequently, we write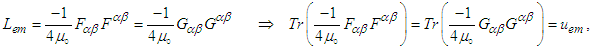 | (99) |
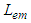 is not zero in free space. This is physically realistic because electromagnetic waves transfer energy and momentum, which are the intrinsic properties of free space. Trace of product of covariant and contravariant Faraday tensors and of their duals in frames
is not zero in free space. This is physically realistic because electromagnetic waves transfer energy and momentum, which are the intrinsic properties of free space. Trace of product of covariant and contravariant Faraday tensors and of their duals in frames 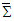 and
and 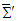 are
are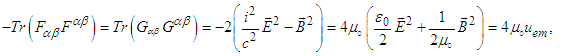 | (100a) |
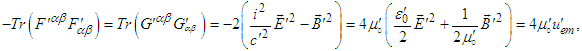 | (100b) |
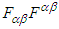 and of their duals
and of their duals 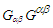 are Lorentz invariant between frames
are Lorentz invariant between frames  and
and  . Meanwhile the trace of product of covariant (contravariant) Faraday tensors and of dual Faraday tensors are also invariant between the massive inertial frames
. Meanwhile the trace of product of covariant (contravariant) Faraday tensors and of dual Faraday tensors are also invariant between the massive inertial frames  and
and 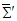 , written as
, written as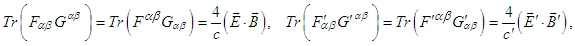 | (101) |
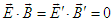 , and
, and 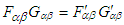 ,
, 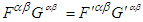 are invariant.
are invariant.10.3. Symmetric Electromagnetic Energy-Momentum Tensor and Conservation Laws
- In section 9 we used the symmetric electromagnetic field energy-momentum tensor to prove the invariance of the conservation of electromagnetic energy and linear momentum. We now extend this idea to cases under spatial rotations of planes about a fixed axis. For example, applying the 4-vector differentiation operator
 , we can extend Eq. (93) to
, we can extend Eq. (93) to 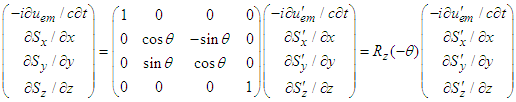 | (102) |
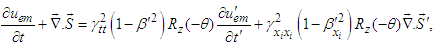 | (103) |
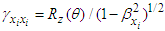 and
and 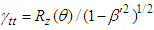 for the spatial rotation dependent space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without rotation, and transforms covariant Eq. (103) into invariant form
for the spatial rotation dependent space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without rotation, and transforms covariant Eq. (103) into invariant form | (104) |
 and chain rule in Eqs. (61) and (62) we can extend Eq. (95) to the following equation for conservation of linear momentum
and chain rule in Eqs. (61) and (62) we can extend Eq. (95) to the following equation for conservation of linear momentum 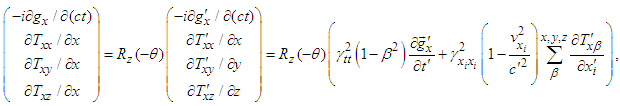 | (105) |
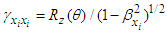 and
and 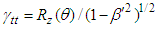 for space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without spatial rotation and transforms covariant Eq. (105) into invariant form. Following the similar steps to produce Eq. (104), we can write the conservation equations along the y- and z-components of linear momentum. Adding x, y and z components we write the following differential equation for 4-vector linear momentum conservation in the generalized 4-dimensional spacetime frame
for space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without spatial rotation and transforms covariant Eq. (105) into invariant form. Following the similar steps to produce Eq. (104), we can write the conservation equations along the y- and z-components of linear momentum. Adding x, y and z components we write the following differential equation for 4-vector linear momentum conservation in the generalized 4-dimensional spacetime frame | (106) |
10.4. Symmetric Electromagnetic Energy-Momentum Tensor for Field Transformation
- It is also instructive to see if the use of the symmetric electromagnetic field energy-momentum tensor can be used to transform electromagnetic fields between two massive inertial frames
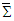 and
and 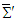 . We try this by using the counterclockwise rotation of (x, y) plane about the z-axis in Eq. (52) and the transformation
. We try this by using the counterclockwise rotation of (x, y) plane about the z-axis in Eq. (52) and the transformation  yields the following symmetric tensor
yields the following symmetric tensor 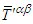 in frame
in frame 
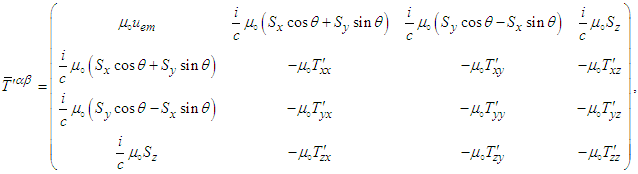 | (107) |
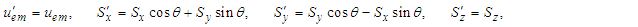 | (108a) |
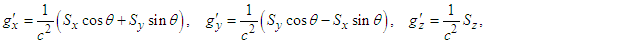 | (108b) |
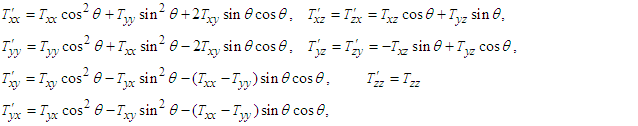 | (108c) |
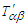 are the components of 3-D Maxwell stress tensor in frame
are the components of 3-D Maxwell stress tensor in frame 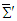 related to those in frame
related to those in frame 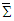 . Equations (108a) and (108b) explicitly demonstrate that the electromagnetic field energy density, Poynting vector and momentum density are Lorentz invariant between frames
. Equations (108a) and (108b) explicitly demonstrate that the electromagnetic field energy density, Poynting vector and momentum density are Lorentz invariant between frames 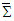 and
and 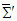 . Furthermore, as a symmetric tensor, trace of energy-momentum tensor
. Furthermore, as a symmetric tensor, trace of energy-momentum tensor 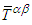 must be zero:
must be zero: 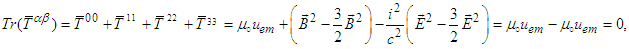 | (109) |
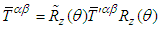 of (x, y) plane about fixed z-axis yields components of the inverse symmetric energy-momentum tensor in frame
of (x, y) plane about fixed z-axis yields components of the inverse symmetric energy-momentum tensor in frame 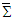 . Since
. Since 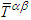 is derived from average sum of the tensor product of covariant and transpose of contravariant (vice versa) and of their duals, it is imperative to confirm that, and by back substitution we should be able to determine the Lorentz invariant electric and magnetic fields between frames
is derived from average sum of the tensor product of covariant and transpose of contravariant (vice versa) and of their duals, it is imperative to confirm that, and by back substitution we should be able to determine the Lorentz invariant electric and magnetic fields between frames 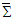 and
and 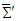 . Matching both sides of Eq. (107) and of its inverse, which is not written here to save space, for
. Matching both sides of Eq. (107) and of its inverse, which is not written here to save space, for 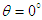 one obtains the following matrix equations for the Cartesian components of the electric and magnetic fields in frame
one obtains the following matrix equations for the Cartesian components of the electric and magnetic fields in frame  those in frame
those in frame 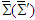 ,
, 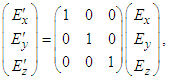 | (110a) |
 | (110b) |
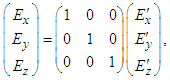 | (110c) |
 | (110d) |
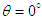 . We can then conclude that
. We can then conclude that 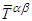 can reliably be used to find Lorentz invariant electric and magnetic field according to
can reliably be used to find Lorentz invariant electric and magnetic field according to 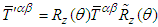 transformation for spatial rotation of (x, y) plane about the fixed z- axis, between two frames. This confirms the Lorentz invariance of symmetric electromagnetic field energy-momentum tensor between two massive inertial frames
transformation for spatial rotation of (x, y) plane about the fixed z- axis, between two frames. This confirms the Lorentz invariance of symmetric electromagnetic field energy-momentum tensor between two massive inertial frames 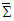 and
and 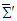 .Since Eq. (78) is representing the classical symmetric energy- momentum tensor and is described by using the 4-dimensional relativistic analogue of 3-dimensional Maxwell’s stress tensor [4], it is also imperative to see whether it also confirms the Lorentz invariance and trace characteristics described for the symmetric electromagnetic energy-momentum tensor in Eq. (107). This is expected since
.Since Eq. (78) is representing the classical symmetric energy- momentum tensor and is described by using the 4-dimensional relativistic analogue of 3-dimensional Maxwell’s stress tensor [4], it is also imperative to see whether it also confirms the Lorentz invariance and trace characteristics described for the symmetric electromagnetic energy-momentum tensor in Eq. (107). This is expected since 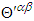 is also a symmetric tensor just like
is also a symmetric tensor just like 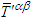 . In the framework of the classical Faraday field transformation, Lorentz invariance of the symmetric electromagnetic energy-momentum tensor
. In the framework of the classical Faraday field transformation, Lorentz invariance of the symmetric electromagnetic energy-momentum tensor 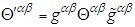 in the massive inertial frame
in the massive inertial frame  is written as
is written as | (111) |
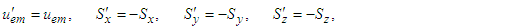 | (112a) |
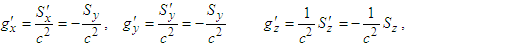 | (112b) |
 | (112c) |
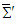 and
and 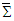 . This contradicts Lorentz transformation which requires all components of relativistic vector quantities must be invariant. Since
. This contradicts Lorentz transformation which requires all components of relativistic vector quantities must be invariant. Since 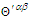 is a symmetric tensor, its trace is zero. However, in the case of trigonometric circular Lorentz boost along the x-axis given by Eq. (48), applying
is a symmetric tensor, its trace is zero. However, in the case of trigonometric circular Lorentz boost along the x-axis given by Eq. (48), applying  in Eq. (78) one obtains symmetric tensor in frame
in Eq. (78) one obtains symmetric tensor in frame 
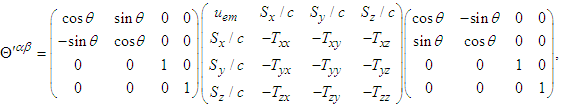 | (113) |
 symmetric energy-momentum tensor
symmetric energy-momentum tensor 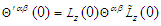 in Eq. (113) yields
in Eq. (113) yields 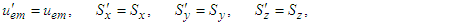 | (114a) |
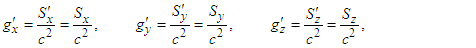 | (114b) |
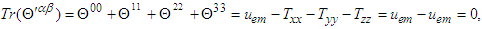 | (114c) |
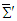 and
and 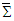 . Furthermore, since
. Furthermore, since 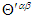 is a symmetric tensor, Eq. (114c) predicts that trace of
is a symmetric tensor, Eq. (114c) predicts that trace of 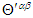 is zero in both frames, confirming that
is zero in both frames, confirming that 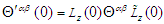 and
and 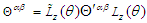 are symmetric electromagnetic energy-momentum tensors. Component by component matching both sides of Eq. (113) and of its inverse for
are symmetric electromagnetic energy-momentum tensors. Component by component matching both sides of Eq. (113) and of its inverse for 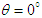 , one obtains the matrix equations (110a), (110b), (110c), and (110d) for Cartesian components of the electric and magnetic fields in frame
, one obtains the matrix equations (110a), (110b), (110c), and (110d) for Cartesian components of the electric and magnetic fields in frame 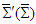 in terms of those in frame
in terms of those in frame 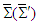 . We conclude that using symmetric energy-momentum tensor is the most reliable way of finding invariant electric and magnetic fields for (i) the spatial rotation of planes about a fixed axis, and (ii) the circular Lorentz boost along the direction of motion and between two reference frames.
. We conclude that using symmetric energy-momentum tensor is the most reliable way of finding invariant electric and magnetic fields for (i) the spatial rotation of planes about a fixed axis, and (ii) the circular Lorentz boost along the direction of motion and between two reference frames. 10.5. Symmetric Electromagnetic Energy-Momentum Tensor and Angular Momentum
- Symmetrical electromagnetic field energy-momentum tensor is needed when we consider the conservation of angular momentum of the electromagnetic field [4]. We can write the angular momentum density of electromagnetic field in the following integral and tensor form [4]
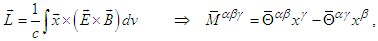 | (115) |
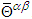 in Eq. (78) is based on the mixed tensors
in Eq. (78) is based on the mixed tensors 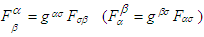 which has no explicit symmetry characteristics [4]: it is neither symmetric nor asymmetric. Consequently, the symmetric angular momentum tensor must be constructed from the symmetric electromagnetic field energy-momentum tensor
which has no explicit symmetry characteristics [4]: it is neither symmetric nor asymmetric. Consequently, the symmetric angular momentum tensor must be constructed from the symmetric electromagnetic field energy-momentum tensor 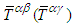 , which is defined according to equation (83), as the average sum of the product of covariant (contravariant) and transpose of contravariant covariant) Faraday tensors and of their duals,
, which is defined according to equation (83), as the average sum of the product of covariant (contravariant) and transpose of contravariant covariant) Faraday tensors and of their duals, 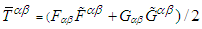 . Therefore, symmetric angular momentum density of electromagnetic field must be defined as
. Therefore, symmetric angular momentum density of electromagnetic field must be defined as 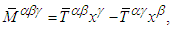 | (116) |
 | (117) |
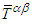 is symmetric, then first and third terns n Eq. (117) can be eliminated and
is symmetric, then first and third terns n Eq. (117) can be eliminated and 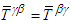 , which proves that conservation of angular momentum of electromagnetic field is symmetric.
, which proves that conservation of angular momentum of electromagnetic field is symmetric.10.6. Symmetric Electromagnetic Energy-Momentum Tensor and Einstein Field Equation
- The proposed use of Faraday tensor, its dual, and symmetric electromagnetic energy-momentum tensor and its dual can have profound effect in the solution of Einstein equation [19]-[21], written as
 | (118) |
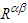 is the Ricci curvature tensor with R being the scalar curvature, and
is the Ricci curvature tensor with R being the scalar curvature, and 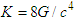 is the gravitational constant. In free space
is the gravitational constant. In free space 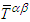 is the fundamental source of the electromagnetic and gravitational fields. Since
is the fundamental source of the electromagnetic and gravitational fields. Since  is symmetric, then
is symmetric, then 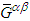 must be symmetric, so that we can write
must be symmetric, so that we can write 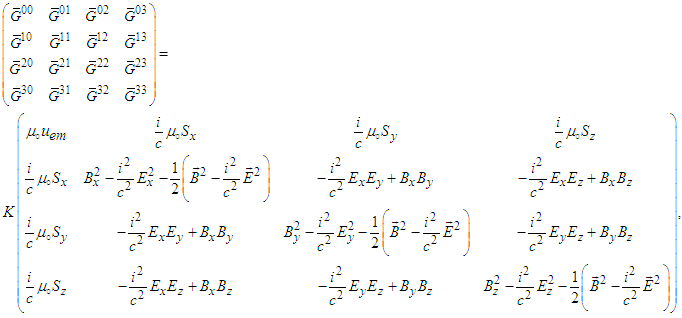 | (119) |
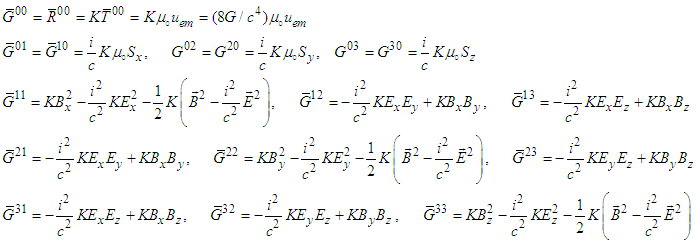 | (120) |
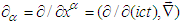 we can write
we can write 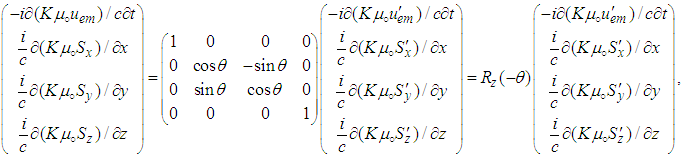 | (121) |
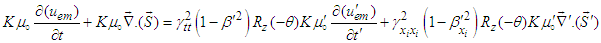 | (122) |
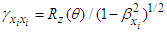 and
and 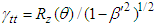 for the spatial rotation dependent space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without rotation, and transforms covariant Eq. (122) into invariant form in which is the Lorentz invariant classical differential form of Poynting theorem in free space.It is also important to point out that conservation of electromagnetic energy and linear momentum equations can also be written for the trigonometric circular Lorentz boost along the direction of motion following the steps to write Eq. (122). For a circular boost along the x-axis, we write the following matrix equation for the Poynting theorem under rotational boost
for the spatial rotation dependent space and time components of Lorentz scaling factor, which reduce to those in Eq. (10) without rotation, and transforms covariant Eq. (122) into invariant form in which is the Lorentz invariant classical differential form of Poynting theorem in free space.It is also important to point out that conservation of electromagnetic energy and linear momentum equations can also be written for the trigonometric circular Lorentz boost along the direction of motion following the steps to write Eq. (122). For a circular boost along the x-axis, we write the following matrix equation for the Poynting theorem under rotational boost | (123) |
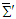 . Using Einstein’s gravitational field equation (118) we write
. Using Einstein’s gravitational field equation (118) we write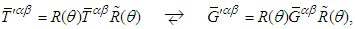 | (124) |
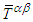 is Lorentz invariant, then
is Lorentz invariant, then  must also be invariant between frames
must also be invariant between frames 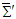 and
and 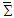 . In other words, Einstein field equation must also be Lorentz invariant between frames
. In other words, Einstein field equation must also be Lorentz invariant between frames  and
and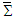 , written as
, written as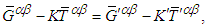 | (125) |
11. Conclusions
- We introduced a four-dimensional generalized Minkowski spacetime frame in which the space and time coordinates are linearly interrelated. After satisfying Lorentz invariance of metric equation between two massive inertial frames, we used classical vector transformation to derive general expressions for Cartesian components of the relativistic velocity, which is valid at any speed, including the speed of light. Considering two massive inertial frames form a closed and isolated system in four dimensional spacetime, we integrated the relativistic velocity components with conservation of energy and new way of using Faraday tensor and its dual in Minkowski space-time to prove that the electric and magnetic fields are Lorentz invariant under circular boost and spatial rotation of planes about a fixed axis. We demonstrate that the product of covariant and contravariant Faraday tensors and of their duals lead to non-zero electromagnetic field Lagrange density in free space, which is physically realistic since electromagnetic fields carry energy and momentum while they propagate free space. We derived analytical expressions for Lorentz invariant Maxwell’s equations, current continuity equation, and symmetric electromagnetic energy-momentum tensor between two inertial frames, with and without source. We further demonstrated that symmetric energy-momentum tensor can be used have a reliable derivation of Lorentz invariant electromagnetic fields between two inertial frames in the case of circular Lorentz boost and spatial rotation about a fixed coordinate axis. We believe that the proposed theory may have profound effect in creating new research areas in theoretical physics.
Data Availability Statement
- This manuscript has no associated data, or the data will not be deposited.
APPENDIX I. Time Dilation, Doppler Shift, and Energy Dispersion Relation
- Using Eq. (9) for the general form of four-covariant metric equation under Lorentz transformation, we write
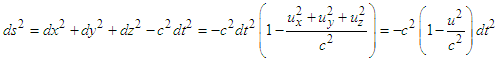 | (A1a) |
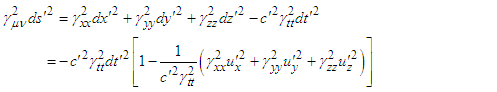 | (A1b) |
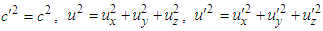 . Matching of Eqs. (A1a) and (A1b) yields
. Matching of Eqs. (A1a) and (A1b) yields 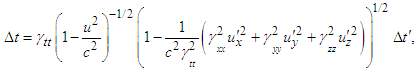 | (A2) |
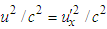 and
and 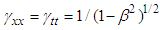 , Eq. (A2) reduces to
, Eq. (A2) reduces to 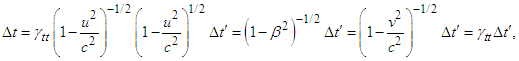 | (A3) |
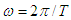 , Eq. (A3) allows us to write the following expression for the relativistic invariance of Doppler shift between two massive inertial frames under Lorentz transformation
, Eq. (A3) allows us to write the following expression for the relativistic invariance of Doppler shift between two massive inertial frames under Lorentz transformation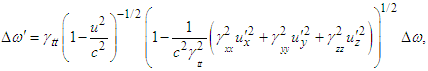 | (A4) |
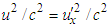 and
and 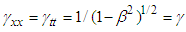 . Eq. (A4) reduces to
. Eq. (A4) reduces to 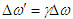 for the relativistic Doppler shift in the classical four-dimensional spacetime theory.Recall that Ives and Stilwell [22] who observed the wavelength of hydrogen atom emitted by canal rays with and against their motion by using a mirror and discovered the frequencies of displaced lines of incoming and outgoing light rays and their average are given by [23]
for the relativistic Doppler shift in the classical four-dimensional spacetime theory.Recall that Ives and Stilwell [22] who observed the wavelength of hydrogen atom emitted by canal rays with and against their motion by using a mirror and discovered the frequencies of displaced lines of incoming and outgoing light rays and their average are given by [23] 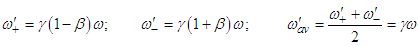 | (A5) |
 and wave vectors
and wave vectors  in the massive inertial frames
in the massive inertial frames  and
and  , respectively, with wave functions
, respectively, with wave functions 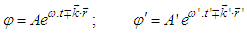 | (A6) |
 and
and 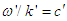 in the massive inertial frames
in the massive inertial frames 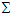 and
and 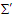 , respectively. With Lorentz invariant phases of plane waves
, respectively. With Lorentz invariant phases of plane waves 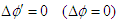 between
between 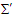 and
and 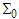 (
(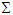 and
and 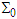 ), we can write
), we can write 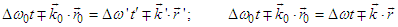 | (A7) |
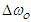 is the incremental shift in the angular frequencies of plane waves in stationary inertial frame
is the incremental shift in the angular frequencies of plane waves in stationary inertial frame 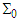 .
.  and
and 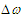 are the incremental shifts in
are the incremental shifts in 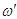 and
and 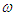 in frames
in frames 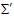 and
and 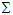 . Using the generalized time
. Using the generalized time 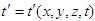 and velocity, equalities in Eq. (A7) lead to
and velocity, equalities in Eq. (A7) lead to  | (A8a) |
 | (A8b) |
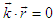 and
and 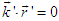 , which can be proven by using
, which can be proven by using  and
and 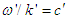 , and spacetime coordinate equations. Doppler shifts in the angular frequencies of forward and inverse plane waves and their averages in the massive inertial frames
, and spacetime coordinate equations. Doppler shifts in the angular frequencies of forward and inverse plane waves and their averages in the massive inertial frames 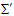 and
and 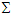 are then written as
are then written as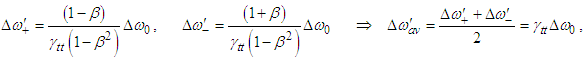 | (A9a) |
 | (A9b) |
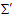 and
and 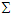 are then written as
are then written as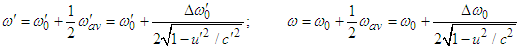 | (A10) |
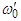 and
and  are the background angular frequencies and
are the background angular frequencies and 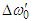 and
and 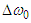 are the Doppler shifts with
are the Doppler shifts with 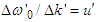 and
and 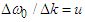 . Multiplying
. Multiplying  and
and  with
with 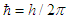 and using
and using 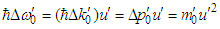 and
and  , one can write
, one can write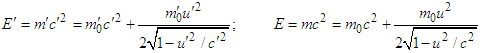 | (A11) |
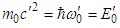 and
and 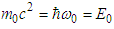 are the rest energies of a particle in
are the rest energies of a particle in 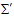 and
and 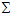 .
. APPENDIX II. Relativistic Mass and Energy Dispersion Relation
- Expressions for relativistic mass and energy are derived by considering the differential change in the energy of a particle moving under the influence of a force in frames
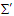 and
and  as [10], [11]
as [10], [11] 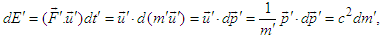 | (A12a) |
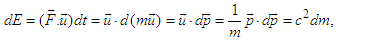 | (A12b) |
 | (A13) |
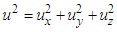 with
with 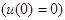 and
and 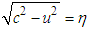 in the massive inertial frame
in the massive inertial frame  and
and 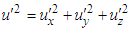 with
with  and
and 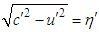 in the massive inertial frame
in the massive inertial frame 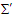 . The result integrals in Eq. (A13) give the relativistic masses in the massive inertial frames
. The result integrals in Eq. (A13) give the relativistic masses in the massive inertial frames 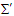 and
and 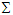
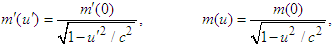 | (A14) |
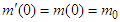 and
and  are rest mass and initial velocities in both frames. Since
are rest mass and initial velocities in both frames. Since 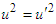 , the relativistic mass is Lorentz scalar
, the relativistic mass is Lorentz scalar 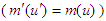 in both frames. The relativistic energy dispersion relations for a particle moving under the influence of a force in the
in both frames. The relativistic energy dispersion relations for a particle moving under the influence of a force in the 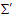 and
and 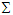 frames are found from the integrals of Eqs. (A12a) and (A12b) that are written as
frames are found from the integrals of Eqs. (A12a) and (A12b) that are written as 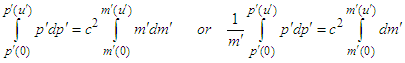 | (A15a) |
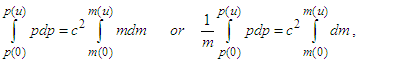 | (A15b) |
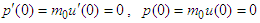 and
and 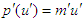 , and
, and 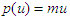 , respectively. Evaluating the first integrals in Eqs. (A15a) and A15b), then multiply both sides by
, respectively. Evaluating the first integrals in Eqs. (A15a) and A15b), then multiply both sides by 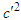 and
and  , and finally taking square root of the final results, one finds Einstein energy dispersion relation
, and finally taking square root of the final results, one finds Einstein energy dispersion relation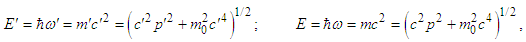 | (A16) |
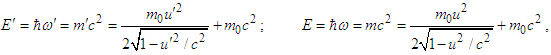 | (A17) |
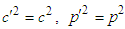 , and
, and 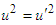 , relativistic energy is Lorentz scalar
, relativistic energy is Lorentz scalar 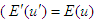 , which suggests that vector transformation does not affect the relativistic invariance of energy. Dividing both sides of Eqs. (A16) and (A17) with
, which suggests that vector transformation does not affect the relativistic invariance of energy. Dividing both sides of Eqs. (A16) and (A17) with 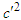 and
and 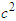 ,we and write
,we and write  | (A18a) |
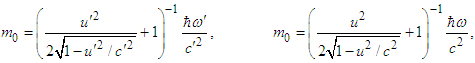 | (A18b) |
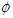 , and (i)
, and (i) 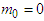 at speed of light
at speed of light 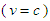 when nonstationary frame moves parallel to ±x axes
when nonstationary frame moves parallel to ±x axes 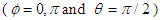 of stationary frame and (ii)
of stationary frame and (ii) 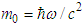 at v=0 as its limiting case at any angle
at v=0 as its limiting case at any angle 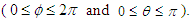 The first result (i) proves that a relativistic particle has zero mass as it moves with the speed of light, frame independent. The energy dispersion relation (A16) becomes equal to
The first result (i) proves that a relativistic particle has zero mass as it moves with the speed of light, frame independent. The energy dispersion relation (A16) becomes equal to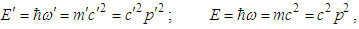 | (A19) |
 at f=7.41x10-4Hz. Equations (A18a) and (A18b) predict
at f=7.41x10-4Hz. Equations (A18a) and (A18b) predict 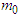 = 4.34x10-55kg suggesting that a particle at rest having a small magnitude but never zero. Comparison shows a good agreement with measurements [24] and astronomical observations [25].The second result (ii) is compared with the prediction of Heisenberg uncertainty principle in rest frame, which yields an upper bound for the rest mass of photon
= 4.34x10-55kg suggesting that a particle at rest having a small magnitude but never zero. Comparison shows a good agreement with measurements [24] and astronomical observations [25].The second result (ii) is compared with the prediction of Heisenberg uncertainty principle in rest frame, which yields an upper bound for the rest mass of photon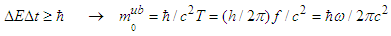 | (A20) |
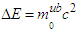 is the photon rest energy and
is the photon rest energy and 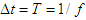 . Notice that that the prediction of Eqs. (A18a) and (A18b) is
. Notice that that the prediction of Eqs. (A18a) and (A18b) is  times higher than that predicted by Eq. (A20] Equations (A18) and (A18n) give
times higher than that predicted by Eq. (A20] Equations (A18) and (A18n) give 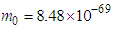 kg, compared with
kg, compared with 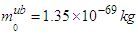 due to Eq. (A20) at
due to Eq. (A20) at 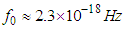 , where
, where 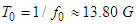 year is the estimated age of the universe [26].
year is the estimated age of the universe [26]. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
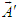 and
and 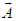 in terms of unit vectors in a counterclockwise rotation in frame
in terms of unit vectors in a counterclockwise rotation in frame  through angle
through angle 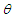 into frame
into frame 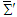 plane (a) and in clockwise rotation in frame
plane (a) and in clockwise rotation in frame 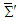 through angle
through angle 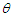 in clockwise direction into frame
in clockwise direction into frame 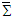 (b) for
(b) for 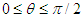
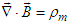 [4] without any proof or experimental evidence about the existence of magnetic charge in literature [15]. Hypothetical magnetic charge density can be derived by combining
[4] without any proof or experimental evidence about the existence of magnetic charge in literature [15]. Hypothetical magnetic charge density can be derived by combining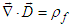 and
and 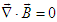 (with
(with 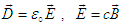 , and
, and 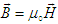 ) to write
) to write  , which allows us to write
, which allows us to write 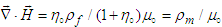 where
where 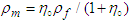 is so called hypothetical magnetic charge density and
is so called hypothetical magnetic charge density and 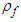 is the static free electric charge density, and
is the static free electric charge density, and 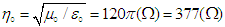 is called “intrinsic impedance” of free space [18]. This hypothetical derivation is not used to derive symmetric Maxwell’s equations in this work since there is still no experimental evidence about the existence of magnetic charge [15].
is called “intrinsic impedance” of free space [18]. This hypothetical derivation is not used to derive symmetric Maxwell’s equations in this work since there is still no experimental evidence about the existence of magnetic charge [15].